第八章方差分析

第一节 方差分析的基本思想
看一个例子
例8-1 为研究钙离子对体重的影响作用，某研究者将36 只肥胖模型大白鼠随机分为三组，每组12只，分别给 予高脂正常剂量钙(0.5%)、高脂高剂量钙(1.0%)和高 脂高剂量钙(1.5%)三种不同的饲料，喂养9周，测其 喂养前后体重的差值。问三组不同喂养方式下大白鼠 体重改变是否不同？
• 三种喂养方式体重改变的平均值各不相同，这种变异 称为组间变异
•
是组内均值
X
与总均值
i
X
之差的平方和
360
340
组间变异反映了：
320
三种喂养方式的差异（影响）， 300
同时也包含了随机误差。
280
260
240
k ni
220
SS组间
(Xi X )2
200
i1 j
180
X甲
X
X乙
X丙
甲
乙
丙
3、组内变异(SS组内，variation within groups)
0.05
2、根据公式计算SS、MS及F值，列于方差分析表内(计 算过程省略)
变异来源 总变异 组间 组内（误差）
完全随机设计的方差分析表
平方和 SS 自由度
均方MS
47758.32
35
31291.67
2
15645.83
16466.65
33
498.99
F值
31.36
3、确定P值，作出判断
分子自由度=k-1=2，分母自由度=n-k=33，查F 界值表（方差分析用）
表 8-1 三种不同喂养方式下大白鼠体重喂养前后差值(g)
正常钙(0.5%) 高剂量钙(1.0%) 高剂量钙(1.5%)

1 10, 2 10
F 分布曲线
17
F 界值表
5
附表5 F界值表（方差分析用，单侧界值） 上行：P=0.05 下行：P=0.01
分母自由度 υ2
•
分子旳自由度，υ1
1
2
3
4
5
6
161 200 216 225 230 234 1
4052 4999 5403 5625 5764 5859
18.51 19.00 19.16 19.25 19.30 19.33 2
t Yi Yh Se
Yi Yh
,
MS组内（
1 n1
1 n2
）
N a 组内
29
例四个均值旳Bonferroni法比较
设α＝α’/c＝0.1/6=0.0167,由此t旳临 界值为t（0.0167/2,20）=2.6117
18.5 28.0
t(A: B)
3.48 2.6117, 24 4 20
以F命名，故方差分析 又称 F 检验 （F
test）。用于推断两 个或多种总体均数有 无差别 。
3
方差分析旳优点： 不受比较组数旳限制，可比较多组均数 可同步分析多种原因旳作用 可分析原因间旳交互作用
4
完全随机设计资料（单原因）方差分析 One-way analysis of variance 第一节 方差分析旳基本思想
deviations from mean，SS)反应变异旳大小
10
1. 总变异: 全部测量值之间总
旳变异程度，计算公式
a ni
SS总
Yij Y
2
Y a ni 2 ij
C
i1 j1
i1 j1
N

SSE xij xi
k ni i 1 j 1
2
计算结果为： SSE = 2708
三个离差平方和的关系
总离差平方和(SST)、组内离差平方和(SSE) 、组间离差平方和 (SSA) 之间的关系：
x
k i 1 j 1
ni
ij
x ni xi x xij x
外包装底色对产品销量是否有显著影响？
市场 北京 上海 深圳 西安 成都 红色 36 35 27 29 38 橙色 28 26 31 30 24 紫色 30 32 28 26 35 蓝色 22 27 20 21 29
什么是方差分析?
【 例 】为了对几个行业的服务质量进行评价，消费者协会 在4个行业分别抽取了不同的企业作为样本。最近一年中消 费者对总共23家企业投诉的次数如下表：

2.
方差分析的基本假定
1. 每个总体都服从正态分布 （每个行业被投诉的次数必须服从正态分布） 2. 各个总体的方差相同 （ 4个行业被投诉次数的方差都相等） 3. 观测值是独立的 （每个行业被投诉的次数与其他行业被投诉的次数独立）
方差分析的基本假设
H 0 : m1 m2 mk H1 : m1 , m2 , , mk 不全相等
2.计算误差
计算全部观测值的均值以及各水平下的组均值 计算总误差 计算组内误差 计算组间误差
计算总误差（ SST）
1. 全部观察值 xij 与总平均值 x 的离差平方和 2. 反映全部观察值的离散状况 3. 其计算公式为
SST xij x
k ni i 1 j 1 2
方差分析
差异源
组间 组内
SS
1456.609 2708

t检验判断两组数据平均数间的差异显著性；方差分 析可同时判断多组数据平均数间的差异显著性。
方差分析的基本原理
在一个多处理试验中，可以得出一系列不同的观测值。 造成观测值不同的原因是多方面的，有的是处理不同引起 的，处理效应或条件变异，有的是试验过程中偶然性因素 的干扰和测量误差所致，既试验误差。方差分析的基本思 想是将测量数据的总变异按照变异原因不同分解为处理效 应和试验误差，并作出其数量估计。 通过方差比较以确 定各种原因在总变异中所占的重要程度，即用处理效应和 试验误差在一定意义下进行比较，如二者相差不大，说明 试验处理对指标影响不大，如二者相差较大，处理效应比 试验误差大得多，说明试验处理影响是很大的，不可忽视。 从而作为统计推断。
变差na来源5 5 平方和 自由度
均方每一个xij都F减去65
SST
处= 理a
误差i=1
n j =1
xi2j 13C1.7=4277 .28 4129 .96
25.58
20
=3124.794.32
0.78
42.23**
S*S*A
总1和 a = α=n0.i0=11
xi2.
1C47=.312308 5
计之前就要明确关于模型的基本假设。对于单因素方差分析 来说，两种模型无多大区别。
第八章 单因素方差分析
三、单因素方差分析的检验及例题验算
（得样一本固）的定方方效差式应分不模同型析，与的致随检使机验所效程得应结模序论型不方同差。分随析机的效程应序模完型全适一用样于，水但平由的于总获 体1，、而正固规定检效验应模程型序只适用于所选定的α个水平。也就是说，随机效应 模2型、Ⅰ可单推因方断素差总方齐体状差性况分检，析验而的固实定效战应检模验型程不序能推断总体状况。

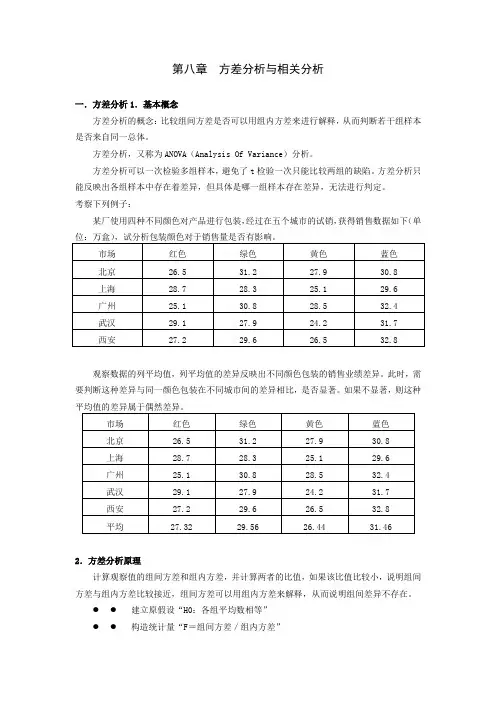
第八章方差分析与相关分析一．方差分析1．基本概念方差分析的概念：比较组间方差是否可以用组内方差来进行解释，从而判断若干组样本是否来自同一总体。

方差分析，又称为ANOVA（Analysis Of Variance）分析。

方差分析可以一次检验多组样本，避免了t检验一次只能比较两组的缺陷。

方差分析只能反映出各组样本中存在着差异，但具体是哪一组样本存在差异，无法进行判定。

考察下列例子：某厂使用四种不同颜色对产品进行包装，经过在五个城市的试销，获得销售数据如下（单观察数据的列平均值，列平均值的差异反映出不同颜色包装的销售业绩差异。

此时，需要判断这种差异与同一颜色包装在不同城市间的差异相比，是否显著。

如果不显著，则这种2．方差分析原理计算观察值的组间方差和组内方差，并计算两者的比值，如果该比值比较小，说明组间方差与组内方差比较接近，组间方差可以用组内方差来解释，从而说明组间差异不存在。

●●建立原假设“H0：各组平均数相等”●●构造统计量“F＝组间方差／组内方差”●●在计算组间方差时，使用自由度为（r-1），计算组内方差时，使用自由度为（n-r）。

●●F满足第一自由度为（r-1），第二自由度为（n-r）的F分布。

●●查表，若F值大于0.05临界值，则拒绝原假设，认为各组平均数存在差异。

根据方差计算的原理，生成方差分析表如下：其中：组间离差平方和 SSA (Sum of Squares for factor A) ＝39.084误差项离差平方和 SSE (Sum of Squares for Error) ＝76.8455总离差平方和 SST (Sum of Squares for Total)＝115.9295P-value值为0.000466，小于0.05，所以拒绝原假设。

3．双因素方差分析观察下列销售数据，欲了解包装方式和销售地区是否对于销售业绩有影响，涉及到双因素的方差分析。

此时需分别计算SSA、SSB与SSE之间的比值是否超过临界值。

01
确定因子和水平
确定要分析的因子（独立变量） 和因子水平（因子的不同类别或 条件）。
建立模型
02
03
模型假设
根据因子和水平，建立方差分析 模型。模型通常包括组间差异和 组内误差两部分。
确保满足方差分析的假设条件， 包括独立性、正态性和同方差性。
方差分析的统计检验
01
F检验
进行F检验，以评估组间差异是否 显著。F检验的结果将决定是否拒
生物统计-8第八章单因素方差分析
目录
• 引言 • 方差分析的原理 • 单因素方差分析的步骤 • 单因素方差分析的应用 • 单因素方差分析的局限性 • 单因素方差分析的软件实现
01
引言
目的和背景
目的
单因素方差分析是用来比较一个分类变量与一个连续变量的关系的统计分析方法。通过此分析，我们可以确定分 类变量对连续变量的影响是否显著。
VS
多元性
单因素方差分析适用于单一因素引起的变 异，如果存在多个因素引起的变异，单因 素方差分析可能无法准确反映实际情况。 此时需要考虑使用其他统计方法，如多元 方差分析或协方差分析等。
06
单因素方差分析的软件 实现
使用Excel进行单因素方差分析
打开Excel，输入数据。
点击“确定”，即可得到单因素方差分析 的结果。
输出结果，并进行解释和 解读。
谢谢观看
背景
在生物学、医学、农业等领域，经常需要研究一个分类变量对一个或多个连续变量的影响。例如，研究不同品种 的玉米对产量的影响，或者不同治疗方式对疾病治愈率的影响。
方差分析的定义
定义
方差分析（ANOVA）是一种统计技术，用于比较两个或更多组数据的平均值 是否存在显著差异。在单因素方差分析中，我们只有一个分类变量。

V 4.2 3.2 4.8
4
5
1.0
0.8 1.5
-1.3
-1.1 -0.3
1.8
3.5 11.5
4.1
6.0 29.0
3.3
2.5 18.0 总和 57.0
xi
n
xi2
j 1 2 ij
2.25
1.93
9.00
3.4
132.25
29.43
841.00 324.00
174.46 68.06
1308.50
sx MS e n
品系号
Ⅳ
Ⅴ
Ⅲ
Ⅱ
Ⅰ
平均数
70.8
68.6
67.3
65.3
64.4
顺序号
1
2
3
4
5
df
k
R0.05
Rk
R0.01
Rk
2
2.95
1.165
4.02
1.588
3 20 4
3.10
1.225
4.22
1.667
3.18
1.256
4.33
1.710
5
3.25
1.284
4.40
1.738
5
单因素固定效应模型方差分析表
变异来源
处理间
平方和
自由度
均方
F
F MS A MS e
SSA
a-1
MSA
误差或处理内
总和
SSe
SST
na-a
na-1
MSe
4、平方和的简易计算方法
株号 1 2 3 I -0.4 0.3 -0.2
品 II

xij (i 1,2,, r , j 1,2,, s)
1 r s 1 s 记＝ ij 表示总平均值， i .＝ ij 表示因素A的第i个水平的平均值， . rs i 1 j 1 s j 1
1 r . j＝ ij 表示因素B的第j个水平的平均值 . r i 1
行业类型 计算机
3.94 2.76 8.95 3.23
每股净收益
3.04 4.69 1.52 5.05
医药
公用
2.89
-2.26
1.65
0.66
2.59
2.22
1.09
1.77
-1.07
-0.15
2.30
2.10
-3.10
2.89 1.12 -3.21 2.11
例8.3：某汽车销售商欲了解三种品牌的汽车X,Y,Z和四种标
ANOVA过程简介
ANOVA过程用于均衡数据的方差分析。
对非均衡数据的方差分析问题，SAS系统要求用GLM（一般 线性模型）来处理（单因素时也可以用ANOVA).
GLM过程也可以处理均衡数据的方差分析问题，但效率低于 ANOVA.
ANOVA过程简介
ANOVA过程的一般格式：
PROC ANOVA<options>; CLASS variables; MODEL dependents=effects</options>; BY variables; FREQ variable; MEANS effects</options>;
一、单因素方差分析模型
设因素X有k个水平，每个水平可视为一个小总体，分别用
X1 , X 2 ,, X k 来表示。记 j的总体均值为 j , X

X ij = m j eij

2
SS t 总变异 df t = N 1
SS b 组间(处理)变异 df b = k 1
SS w 组内(误差)变异 df w = N k
均方
平方和 均方 = 自由度 SS e 组内(误差)均方 MS w = MS e = df e SS b 组间(处理)均方 MSb = MStr = df b
2 e 2 e
m =
j m
2
k 1
=
2 j
k 1
2
当H 0为真时，E MS error = E MStreatm ent 当H 0为假时，E MS error E MStreatm ent
平方和的分解 sum of squares
• 平方和的优越性在于其可加性
– 过程：包含27个词的表过3遍后要求被试写下 记住的词
因素“加工方式”有 5 个水平 j＝ 1 ,2 ,… ,k (k = 5 )
co unting i= 1 ,2 ,… ,n n= 1 0 9 8 6 8 10 4 6 5 7 7 To ta l(Tj) M e an SD V a ria nce 70 7 .0 0 1 .8 3 3 .3 3 rhy ming 7 9 6 6 6 11 6 3 8 7 69 6 .9 0 2 .1 3 4 .5 4 a dje ctiv e 11 13 8 6 14 11 13 13 10 11 110 1 1 .0 0 2 .4 9 6 .2 2 ima g e ry 12 11 16 11 9 23 12 10 19 11 134 1 3 .4 0 4 .5 0 2 0 .2 7 inte ntio na l 10 19 14 5 10 11 14 15 11 11 120 1 2 .0 0 3 .7 4 1 4 .0 0 503 =∑ X 1 0 .0 6 4 .0 1 1 6 .0 6 to ta l

第八章 方差分析
编辑课件
公共卫生系 流行病与统计学教研室
祝晓明
例 8-1 在评价某药物耐受性及安全性的I 期临床试验中，对符合纳入标准的30名健 康自愿者随机分为3组每组10名，各组注 射剂量分别为0.5U、1U、2U，观察48小 时部分凝血活酶时间（s）试问不同剂量的 部分凝血活酶时间有无不同？
编辑课件
编辑课件
• 方差分析
F=3.55， F＞F0.05(2,18)，P<0.05，三组大鼠 MT 含量的总体均值不全相同。
编辑课件
第三节 多个样本均数的两两比较
证实性研究
探索性研究
证实性研究 与探索性研究
编辑课件
Dunnett-t 检验 LSD-t 检验
SNK-q检验 Tukey检验 Schéffe检验
两个均数的比较时，同一资料所得结果与t检验等
价，即有如下关系 t 2 。F
2.方差分析的基本思想：将全部观测值的总变异按 影响因素分解为相应的若干部分变异，在此基础 上，计算假设检验的统计量 F 值，实现对总体均 数是否有差别的推断。
编辑课件
3. 方差分析有多种设计类型，但基本思想和计算步骤 相同，只是分组变量的个数不同,使用统计软件很容 易实现。 4.多重比较有多种方法，如 Dunnett-t 检验、LSD-t检 验、SNK-q (Student-Newman-Keuls)法 、Tukey法、 Schéffe法、Bonferroni t 检验和 Sidak t 检验。学习 中注意各种方法的适用性。
k1
的
2 分布， 2
2 ,
，认为方差不齐。
编辑课件
例8-1 资料方差齐性检验 提出检验假设，确定检验水准 H0：σ12=σ22=σ32 H1：三组方差不全相等 α=0.05

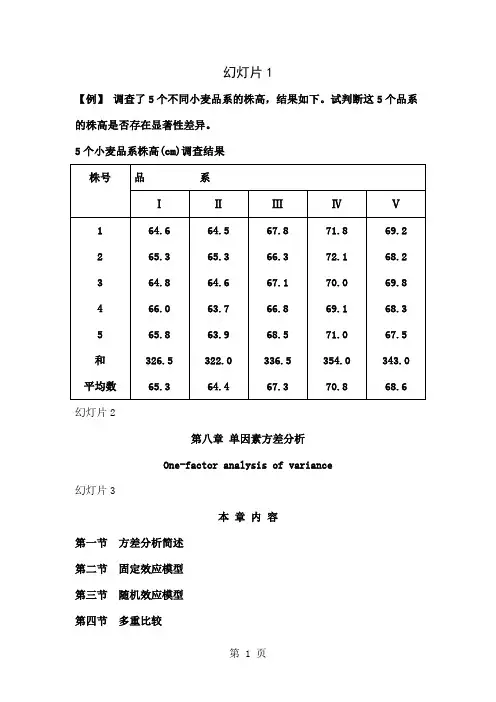
幻灯片1【例】调查了5个不同小麦品系的株高，结果如下。

试判断这5个品系的株高是否存在显著性差异。

5个小麦品系株高(cm)调查结果幻灯片2第八章单因素方差分析One-factor analysis of variance幻灯片3本章内容第一节方差分析简述第二节固定效应模型第三节随机效应模型第四节多重比较第五节方差分析应具备的条件幻灯片4第一节方差分析简述一、方差分析的一般概念1、概念方差分析（ analysis of variance，ANOVA）：是同时判断多组数据平均数之间差异显著性的统计假设检验，是两组数据平均数差异显著性t 检验的延伸。

ANOVA 由英国统计学家R.A.Fisher首创，用于推断多个总体均数有无差异。

幻灯片5单因素方差分析（一种方式分组的方差分析）：研究对象只包含一个因素(factor)的方差分析。

单因素实验：实验只涉及一个因素，该因素有a个水平(处理)，每个水平有n次实验重复，这样的实验称为单因素实验。

水平(level)：每个因素不同的处理(treatment)。

幻灯片6方差分析Analysis of Variance （ANOVA )因素也称为处理因素（factor）（名义分类变量），每一处理因素至少有两个水平(level)（也称“处理组”）。

一个因素（水平间独立）——单向方差分析（第八章）两个因素（水平间独立或相关）——双向方差分析（第九章）一个个体多个测量值——重复测量资料的方差分析 ANOVA与回归分析相结合——协方差分析目的：用这类资料的样本信息来推断各处理组间多个总体均数的差别有无统计学意义。

幻灯片7【例】随机选取4窝动物，每窝中均有4只幼仔，称量每只幼仔的出生重，结果如下。

判断不同窝的动物出生重是否存在显著性差异。

4窝动物的出生重单位：g幻灯片82、单因素方差分析的数据格式：幻灯片9二、不同处理效应与不同模型 1、方差分析中每一观测值的描述——线性统计模型yij ：在第i 水平下的第j 次观测值； μ：总平均数，是对所有观测值的一个参数；αi ：处理效应，是仅限于对第i 次处理的一个参数； εij ：随机误差成分。

615如果进行一个的多因素试验不考虑交互作用完全水平组合试验总数为次若采用正交试验设计最小的试验次数为25611现有三台机器生产同规定的铝合金薄板其厚度分别服从同方差的正态分布从三台机器上各取五块斑测量其厚度对其进行方差分析求得f3292查f分a三台机器生产的薄板厚度在显著性水平095上有显著差异b三台机器生产的薄板厚度在显著性水平095上无显著差异c三台机器生产的薄板厚度在显著性水平005上有显著差异d三台机器生产的薄板厚度在显著性水平005上无显著差异个总体若符合单因子方差分析方法分析数据的假定时所检验的原假设是各总体的变异系数相等方差分析单因子方差分析是在相同方差的假定下检验多个正态总体的均值是否相等的一种统计方法即检验的原假设是三种饲料喂猪得一个月后每猪所增体重单位
• H1： 1 , 2 , , r 不全等。
【案例1】哪种促销方式效果最好？
• 某大型连锁超市为研究各种促 销方式的效果，选择下属 4 个 门店，分别采用丌同促销方式， 对包装食品各迚行了4 个月的 试验。试验结果如下：
超市管理部门希望了解： ⑴丌同促销方式对销售量是否 有显著影响？ ⑵哪种促销方式的效果最好？
X
.j
SS B a X
j 1 a b
b

.j
X

2
SS E
X
i 1 j 1
ij
X
i.
X

2
称为误差平方和，反映试验误差对试验指标的影响。
4. 检验用的统计量
同样可以证明：当 H01 为真时，统计量
FA S A /( a 1 ) S e /( a 1 )( b 1 )
• 问： • （1）不同品种的平均每公顷产 量是否存在显著差异？ （2）任意两个品种的平均每 公顷产量是否都存在显著差异？ 并确定适合该地区的高产小麦 品种。

总
组间＋组内
2024/11/10
西安医学院公共卫生系
01
假设μ1=μ2 即患者与健康人血磷值相同，
02
那么两者的组间变异应该等于组内变异。
03
此时，令F=MS组间 / MS组内 ，
04
则F值理论上应为1。
05
若μ1≠μ2，组间变异便会↑，F↑。
06
查F界值表（附表4），
07
得P值，下结论。
完全随机设计的方差分析
完全随机设
1 计方差分析 中变异的分 解：
组间变异：
4 包括随机误 差和处理因 素的影响
2 总变异分为 两部分
组内变异：
3 反映随机误 差
完全随机设 计的单因素
5 方差分析 （one-way ANOVA）
——成组设
6 计的多个样 本均数的比 较
2024/11/10
西安医学院公共卫生系
二．分析计算步骤：以P47例6.1为例
该设计是将受试对象先按配比条件配成配 伍组（如动物实验时，可按同窝别、同性 别、体重相近进行配伍），每个配伍组有 三个或三个以上受试对象，再按随机化原 则分别将各配伍组中的受试对象分配到各 个处理组。
同一受试对象不同时间（或部位）重复多次 测量所得到的资料称为重复测量数据 （repeated measurement data），对该 类资料不能应用随机区组设计的两因素方差 分析进行处理，需用重复测量数据的方差分 析。
01 例 1 . 某 克 山 病 区 测 得 1 1 例 克 山病患者与13名健康人的血 磷值（mmol/L）如下，问 该地急性克山病患者与健康 人的血磷值是否不同？
02 患 者 x 1 ： 0 . 8 4 ， 1 . 0 5 ， 1.20，1.20，1.39， 1.53，1.67，1.80， 1.87，2.07，2.11。

2.处理内误差(sum of squares for error)，记为SSE § 因素的同一水平下数据误差的平方和 比如，施用A种氮肥下水稻产量的误差平方和
§ 只包含随机误差
3.处理间误差(sum of squares for category)，记为SSC § 因素的不同水平之间数据误差的平方和 比如，不同氮肥下水稻产量之间的误差平方和
2.由误差平方和除以相应的自由度求得 3.三个平方和对应的自由度分别是
▪ SST 的自由度为nk-1，其中nk为全部观察值的个数 ▪ SSt的自由度为k-1，其中k为因素水平的个数 ▪ SSe 的自由度为k（n-1）
8 - 21
第四章 概率论与抽样分布
8.1 方差分析概述
计算均方 MS
1.处理间均方：SSt的均方，记为MSt，计算公式为
▪SST=(242+302+…+212）-13833.8= 402.2
8 - 15
第四章 概率论与抽样分布
8.1 方差分析概述
处理间误差SSt
2、各组平均值 与x总i 平(i均值1,2的,离差, k平) 方和
x
反映各总体的样本均值之间的差异程度
该平方和既包括随机误差，也包括系统误差
计算公式为
ni
k
k
xij x 2 ni xi x 2
ni
xij xi 2
i1 j1
i1
i1 j1
SST = SSC + SSE
▪ 前例的计算结果
402.2=301.2+101.0
8 - 20
第四章 概率论与抽样分布
8.1 方差分析概述
均方(Mean square)
1.各误差平方和的大小与观察值的多少有关，为消除观察值 多少对误差平方和大小的影响，需要将其平均，这就是均 方，记为MS

Q&A
人人思考，大声说出
结束语
感谢参与本课程，也感激大家对我们工作的支持与积极 的参与。课程后会发放课程满意度评估表，如果对我们
课程或者工作有什么建议和意见，也请写在上边
最后、感谢您的到来
· 讲师： XXXX
· 时间：202X.XX.XX
n 两个因素均为随机因素时称为随机模型(random model)；
n 两个因素中一个是固定因素，另一是随机因素时 称为混合模型(mixed model)。
模型类型
n 由于因素水平的改变而引起的平均数的改变量称为主效应。
在多因素试验中， 一个因素的作用要受到另一个因 素的影响，表现为某一因素在另一因素的不同水平上所产 生的效应不同，这种现象称为该两因素存在交互作用。
n 多重比较的方法很多，这里只介绍Duncan法。
Duncan 检验
第三节 方差分析应具备的条件
n 方差分析应满足三个条件
可加性 正态性
xij i ij
方差齐性：各处理的误差方差应具备齐源自，它们有一个公 共的总体方差σ2 。
n 以上三个条件中，方差齐性对分析结果影响最大。 n 因此在做方差分析之前应先做多个方差齐性的检验。只有
表 2 型糖尿病患者治疗4周后餐后2小时血糖的下降值(mmol/L)
n SST=1086.829 n SSA=176.957 n SSe=SST-SSA=909.871 n dfT=N-1=60-1=59 n dfA=a-1=3-1=2 n dfe=dfT-dfA=59-2=57 n MSA=SSA/dfA=176.957/2=88.47855 n MSe=SSe/dfe=909.871/57=15.96266 n F=MSA/MSe=88.47855/15.96266=5.543 n F2,57,0.05=3.167 n F2,57,0.01=5.018

H 0 ： 12 k
H 1： 1， 2， ， k 不全相等
原假设表示在不同的下的各个总体均值相等，即不同的水平对总体均 值没有显著影响；备择假设表示在不同的下的各个总体均值不全相等， 至少有一个总体均值与其它总体均值不等，即该因素的不同的水平对总 体均值存在显著影响。
2021年3月31日/*
《统计学教程》
第8章 方差分析
8.2 单因素方差分析
2．计算均值 （1）水平均值
水平均值（Level Mean）是指根据具体水平下的观察值的均值。一般 将第j项水平的水平均值记为，有计算公式为
x j
1 nj
nj
xij
i 1
（8.1）
（2）总均值
总均值（Total Mean）是指全部观察值的均值，也为水平均值的均值。
《统计学教程》
第8章 方差分析
8.1方差分析的一般问题
例8.1 某企业为了分析研究成品车间的产品质量控制问题，对该车间 的5个班组的产品优等品率进行了一次抽查，在每个班组独立地抽取了5 个优等品率数据构成了随机样本。
表8.1 某企业成品车间5个班组优等品率抽查情况
观察值 1组
班组
2组
3组
4组
81
83
《统计学教程》
第8章 方差分析
8.2 单因素方差分析
3．计算离差平方和
（1）总离差平方和
总离差平方和（Sum of Squares for Total, SST）是指全部观察值与 总均值的离差的平方和，反映了全部观察值离散程度的总规模。有
k nj
SST
xij x 2
j1 i1
（8.3）
按照式（8.3），由表8.2的数据可以计算出例8.1的总离差平方和SST为 286.96。

si2
Ⅰ 122 2500 20.33 3.88
Ⅱ 106 1902 17.67 5.86
k 5 n6
C 6072 6 5 12281.63
Ⅲ 150 3770 25.00 4.00
Ⅳ 137 3165 22.83 7.34
Ⅴ 92 1426 15.33 3.06 T 607 xi2j 12763
第五页，共47页。
因此此时再用t-test法进行检验就不恰当了
如何对 k 3个样本进行假设检验？ 这就是本章所要讨论的方差分析
什么叫方差？
方差是对数据（或称资料）变异的度量
方差的公式：
总一般体总：体 2方 差称xN方2差样，本样：本s方2 差n称x1均x 2 方
x2
n
x
n 1
2
能使变量发生变异的原因很多，这些原因我们都将其称为变
如果这许多样本都只和对照组相比，我们仍然可以使用t-
test或u-test进行，但如果需要样本之间两两相比较的
话，就不能使用t-test或u-test进行了 其理由有以下几个：
第三页，共47页。
1、当有k个样本所属总体的平均值相互两两比较，就需
作
1 k次k比1较 ，即作
2
次1 k假k 设1 检验
2
验结束后每一组内的数据资料相等，这就是组内样 本容量相等的情况
（一）数据结构和数学模型
方差分析是建立在一定的线性数学模型基础上的，所谓线性 模型就是指每一个观测值都可以分割成若干个线性部分， 这是方差分析中平方和、自由度剖分的理论依据
第十三页，共47页。
设从一个 N , 2 中随机抽取一个样本，容量为 ，n这
能充分使用试验中所有的信息量，这是十分可惜的