下载文档原格式
数学的数论及其算术运算数论是数学的一个分支，研究整数的性质和结构，以及整数之间的关系和运算。
它是数学的基础，对于理解和应用其他数学分支都至关重要。
本文将介绍数论的基本概念和算术运算。
一、数论的基本概念1. 整数：整数是自然数、零和负整数的集合，用Z表示。
整数具有封闭性、加法逆元和乘法逆元等性质。
2. 素数：素数是只能被1和自身整除的正整数，例如2、3、5、7等。
素数是数论中的重要研究对象，素数的性质和分布规律一直是数学家们关注的焦点。
3. 最大公约数和最小公倍数：最大公约数是两个或多个整数中能够整除它们的最大正整数，最小公倍数是两个或多个整数中能够被它们整除的最小正整数。
最大公约数和最小公倍数在数论中有广泛的应用，例如化简分数、求解线性方程等。
二、算术运算1. 加法：整数的加法满足交换律、结合律和存在加法逆元等性质。
例如，对于整数a、b和c，有(a+b)+c=a+(b+c)和a+(-a)=0。
2. 减法：减法是加法的逆运算，对于整数a和b，a-b=a+(-b)。
3. 乘法：整数的乘法满足交换律、结合律和存在乘法逆元等性质。
例如，对于整数a、b和c，有(a*b)*c=a*(b*c)和a*(1/a)=1（其中a≠0）。
4. 除法：除法是乘法的逆运算，对于整数a和b，a/b=a*(1/b)。
5. 模运算：模运算是整数除法的一种扩展，对于整数a、b和正整数m，a模m （记作a mod m）是a除以m的余数。
模运算在密码学、计算机科学等领域有广泛的应用。
三、数论的应用1. 密码学：数论在密码学中有重要的应用，例如RSA加密算法就是基于大数分解的难题。
通过选择适当的素数和数论算法，可以实现安全可靠的加密和解密过程。
2. 算法设计：数论算法在计算机科学中起着重要的作用，例如欧几里得算法用于求解最大公约数，扩展欧几里得算法用于求解线性方程的整数解。
3. 数字理论：数论在数字理论中有广泛的应用，例如整数分解、同余方程、数列等。
数论知识点归纳总结数论是数学的一个分支，研究整数及其性质的科学。
它是由数学中最古老的领域之一，也是最重要的领域之一。
数论大部分内容都集中在整数的性质和关系，包括数的性质、数的划分、数的因子、余数、等式、方程等。
数论在许多不同的领域有很多应用，如密码学、加密技术、算法设计、计算机科学等等。
下面将对数论的一些重要知识点进行归纳总结，以便更好地理解和掌握数论的基本概念和方法。
一、整数及其性质1. 整数的性质：整数是由自然数和其相反数构成的有理数。
整数的性质包括奇数和偶数的性质、质数和合数的性质、互质数和最大公约数的性质等等。
2. 除法定理：任意两个整数a和b中，存在唯一的一对整数q和r使得a=bq+r，其中0<=r<|b|。
3. 唯一分解定理：每一个大于1的自然数都可以写成一组素数的乘积。
而且，如果一个数有两种不同的素因数分解形式，那么这两种形式只差一个或若干个单位。
4. 有限整除原理：如果一个整数被另一个不等于0的整数整除，那么这两个整数中一定有一个是整数的最大公因子。
二、数的划分1. 除法和约数：一个整数能被另一个整数整除，那么这个整数就是另一个整数的约数。
2. 素数：只有1和它本身两个因子的自然数，称为素数。
3. 合数：大于1的除了1和它本身以外还有其他因子的数，称为合数。
4. 最大公因数和最小公倍数：两个整数a和b最大的公因数称为a和b的最大公因数，最小的公倍数称为a和b的最小公倍数。
5. 互质数：两个数的最大公因数是1，就称这两个数是互质数。
三、同余和模运算1. 同余性质：如果两个整数a和b除以正整数m所得的余数相等，就称a与b对模m同余。
2. 同余方程：形如ax≡b(mod m)的方程称为同余方程，其中a，b，m都是整数。
3. 欧拉函数：对于任意正整数n，欧拉函数φ(n)是小于或等于n且与n互质的正整数的个数。
4. 模反元素：在模n的情况下，如果一个数a与n互质，那么a关于模n的乘法逆元素x 就是属于[0, n-1]的一个整数，使得ax ≡ 1 (mod n)。
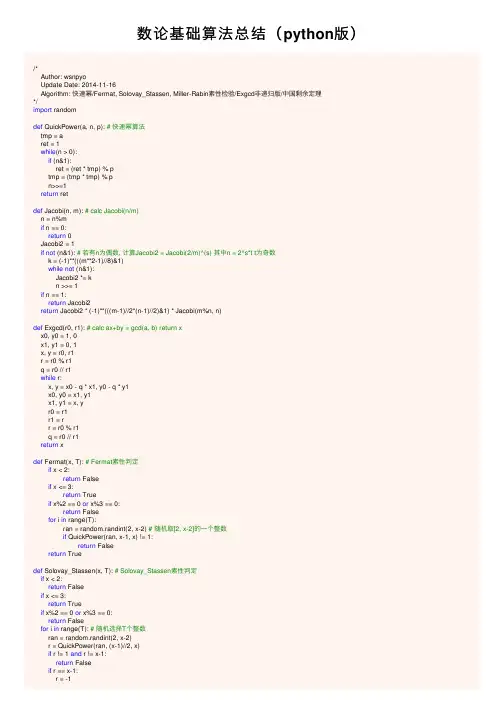
数论基础算法总结（python版）/*Author: wsnpyoUpdate Date: 2014-11-16Algorithm: 快速幂/Fermat, Solovay_Stassen, Miller-Rabin素性检验/Exgcd⾮递归版/中国剩余定理*/import randomdef QuickPower(a, n, p): # 快速幂算法tmp = aret = 1while(n > 0):if (n&1):ret = (ret * tmp) % ptmp = (tmp * tmp) % pn>>=1return retdef Jacobi(n, m): # calc Jacobi(n/m)n = n%mif n == 0:return 0Jacobi2 = 1if not (n&1): # 若有n为偶数, 计算Jacobi2 = Jacobi(2/m)^(s) 其中n = 2^s*t t为奇数k = (-1)**(((m**2-1)//8)&1)while not (n&1):Jacobi2 *= kn >>= 1if n == 1:return Jacobi2return Jacobi2 * (-1)**(((m-1)//2*(n-1)//2)&1) * Jacobi(m%n, n)def Exgcd(r0, r1): # calc ax+by = gcd(a, b) return xx0, y0 = 1, 0x1, y1 = 0, 1x, y = r0, r1r = r0 % r1q = r0 // r1while r:x, y = x0 - q * x1, y0 - q * y1x0, y0 = x1, y1x1, y1 = x, yr0 = r1r1 = rr = r0 % r1q = r0 // r1return xdef Fermat(x, T): # Fermat素性判定if x < 2:return Falseif x <= 3:return Trueif x%2 == 0 or x%3 == 0:return Falsefor i in range(T):ran = random.randint(2, x-2) # 随机取[2, x-2]的⼀个整数if QuickPower(ran, x-1, x) != 1:return Falsereturn Truedef Solovay_Stassen(x, T): # Solovay_Stassen素性判定if x < 2:return Falseif x <= 3:return Trueif x%2 == 0 or x%3 == 0:return Falsefor i in range(T): # 随机选择T个整数ran = random.randint(2, x-2)r = QuickPower(ran, (x-1)//2, x)if r != 1 and r != x-1:return Falseif r == x-1:r = -1if r != Jacobi(ran, x):return Falsereturn Truedef MillerRabin(x, ran): # x-1 = 2^s*ttx = x-1s2 = tx&(~tx+1) # 取出最后⼀位以1开头的⼆进制即2^sr = QuickPower(ran, tx//s2, x)if r == 1 or r == tx:return Truewhile s2>1: # 从2^s -> 2^1 循环s次r = (r*r)%xif r == 1:return Falseif r == tx:return Trues2 >>= 1return Falsedef MillerRabin_init(x, T): #Miller-Rabin素性判定if x < 2:return Falseif x <= 3:return Trueif x%2 == 0 or x%3 == 0:return Falsefor i in range(T): # 随机选择T个整数ran = random.randint(2, x-2)if not MillerRabin(x, ran):return Falsereturn Truedef CRT(b, m, n): # calc x = b[] % m[]M = 1for i in range(n):M *= m[i]ans = 0for i in range(n):ans += b[i] * M // m[i] * Exgcd(M//m[i], m[i])return ans%M以上作为半个学期来数论学习的⼀个⼩结，也许以后难以再系统的学习数论了。
算法概述知识点总结一、算法的概念1. 算法是什么算法（Algorithm）是指用于解决特定问题的一系列具体操作步骤。
它是一种解决问题的方法论，能够将问题的输入转化为输出。
2. 算法的特点（1）确定性：算法在相同的输入条件下，能够得到相同的输出结果。
（2）可行性：算法的每一步操作可以实际执行，不会陷入无穷循环。
（3）有穷性：算法必须在有限的步骤内结束。
（4）输入输出：算法必须具有输入和输出。
3. 算法的重要性算法在计算机科学领域有着重要的地位，它是计算机程序的核心。
一个好的算法能够提高程序的执行效率和准确性，从而提高计算机系统的整体性能。
二、算法的设计方法1. 分治法分治法（Divide and Conquer）是一种算法设计方法，它将问题分解为更小的子问题，通过递归地解决子问题，最终得到原问题的解。
分治法常用于解决大规模问题，例如快速排序、归并排序、最近点对等。
2. 贪心法贪心法（Greedy Algorithm）是一种构造性的算法设计方法，它每次以最优的策略选择当前的最佳解，从而得到问题的整体最优解。
贪心法常用于最优化问题，例如最小生成树、哈夫曼编码等。
3. 动态规划动态规划（Dynamic Programming）是一种通过将问题分解为更小的子问题来解决复杂问题的算法设计方法。
动态规划通过存储子问题的解以减少重复计算，能够有效解决一些复杂的优化问题，例如背包问题、最长公共子序列等。
4. 回溯法回溯法（Backtracking）是一种通过不断试探和放弃来寻找问题解空间的算法设计方法。
回溯法常用于解决一些搜索和排列组合问题，例如全排列、N皇后问题等。
5. 分析设计算法的分析设计是指分析问题的特性和要求，设计出合适的算法来解决问题。
它是算法设计的关键环节，需要充分考虑问题的复杂度、特性和约束条件，从而选择合适的算法设计方法。
三、算法的复杂度分析1. 时间复杂度时间复杂度是算法执行所需时间的度量，它用大O表示法（O）来描述算法执行时间与输入规模之间的关系。
关于数论的简笔-概述说明以及解释1.引言1.1 概述数论是数学的一个分支领域，研究整数及其性质的学科。
作为数学中最古老的分支之一，数论在数学领域具有重要的地位和作用。
从最简单的自然数开始，数论探究整数之间的关系，寻找规律和性质。
数论的研究对象涉及素数、同余、整除性质等，涵盖了许多经典的问题和定理。
本文将介绍数论的定义、基本概念以及在现代科学中的应用，旨在帮助读者更好地了解数论领域的重要性和发展前景。
1.2 文章结构文章结构：本文主要包括引言、正文和结论三个部分。
1. 引言部分主要概括了数论的重要性和应用领域，以及本文的目的和结构安排。
2. 正文部分将详细介绍数论的定义、基本概念和在现代科学中的应用，为读者全面了解数论提供基础知识和案例分析。
3. 结论部分将对数论的重要性进行总结，并展望数论的发展前景，以及呼吁读者加深对数论的理解和研究。
通过以上安排，本文将全面介绍数论这一重要学科，并希望为读者提供更深入的了解和思考。
1.3 目的本文的目的是介绍数论的基本概念和其在现代科学中的应用。
通过对数论的定义、基本理论和应用领域的探讨，希望读者能够了解数论在数学领域的重要性和影响力。
同时，本文也旨在激发读者对数论的兴趣，使他们更深入地了解和研究这一领域，探索数论在未来的发展前景。
通过本文的阐述，读者将能够领略数论的魅力，认识到其在解决现实问题中的潜力，进而促进数论研究的进一步发展。
2.正文2.1 数论的定义数论是研究整数的数学分支，它涉及整数及其性质、特征、性质等方面的研究。
在数论中，研究的对象是整数及其之间的关系，包括整数的性质、因子分解、素数等内容。
数论的研究对象并不仅限于整数，还包括有理数、代数数、超越数等。
数论的研究方法主要包括利用代数、几何、解析方法等进行推导和证明，以及借助计算机等工具进行验证和实验研究。
数论是数学的一门重要研究领域，它不仅具有理论上的重要性，也在密码学、编码理论、算法设计等实际领域有着广泛的应用。
数论（整除、余数）知识点精讲一、整除（1）概念（2）数的整除特征1.尾数判断法：①如果一个整数的个位数字能被2或5整除，那么这个整数能被2或5整除；②如果一个整数的末两位数字能被4或25整除，那么这个整数能被4或25整除；③如果一个整数的末三位数字能被8或125整除，那么这个整数能被8或125整除。
2.数字求和法：如果一个整数各个数位数字之和能被3或9整除，那么这个整数能被3或9整除。
3.奇偶位求差法：如果一个整数的奇数位数字之和与偶数位数字之和的差（大减小）能被11整除，那么这个整数一定能被11整除。
4.三位截断法：“末三位数字组成的数”与“末三位以前的数字组成的数”之差能被7或11或13整除，那么这个数就能被7、11、13整除。
5.分拆成简单数的乘积结合起来判断如一个数能被6整除,那么这个数既是2的倍数，又要是3的倍数。
如此类似的，15=3×5,24=3×86.构造成与整十整百的数的倍数的方法如：判断一个数是不是99的倍数，我们可以先看这个数与100的关系；判断一个数是不是999的倍数，我们可以先看这个数与1000的关系。
二、余数1、利用数的整除特征求余数注意利用11的整除特征求余数时何时余数是a，何时是（11—a）；利用7,13的整除特征时，将六位数截开得到两个三位数的问题。
2、替换求余法：（1）和的余数等于余数的和：两个数的和除以某个数的余数，等于这两个数分别除以这两个数后得到的余数相加后，再除以除数的余数；（2）差的余数等于余数的差，再除以除数的余数：两个数的差除以某个数的余数，等于这两个数分别除以这两个数后得到的余数相减后，再除以除数的余数；（3）积的余数等于余数的积，再除以除数的余数：两个数的乘积除以某个数的余数，等于这两个数分别除以这两个数后得到的余数相乘后，再除以除数的余数。
3、余数的周期性变化：连续自然数除以3的余数按照0,1,2的周期变化，换成其他的除数也有类似规律。
的乘积使用传统的方法至少需要的复杂度，如何加速上述过程？10.1 快速傅里叶变换首先考虑如何用其他方式表示多项式 .任取n个不同的数(可以是整数、实数，甚至是复数)将其代入中，就得到一个线性方程组只要足够大，就能够唯一地确定一个多项式，换言之，上述方程组可以表示一个多项式，将这两种多项式的表示方法分别称为系数表示和点值表示.利用快速傅里叶变换来求多项式乘积的总体思路是1. 选取合适的个不同的数2. 将多项式与转化为点值表示(称为离散傅里叶变换，简称)3. 计算的点值表示4. 将转化为系数表示(称为逆离散傅里叶变换，简称)1. 选取合适的个不同的数我们选取复数域上的个不同的值(或称个次单位复根)作为的值，即至于指数形式的复数，用大家所熟知的欧拉公式即可求得其代数形式经过简单计算可知当为偶数时其中为除以的余数，上述两等式将在后文中使用.我们为什么要费尽周折选取如此复杂的点呢?是为了使用快速傅里叶变换.2. 将多项式与转化为点值表示考虑多项式，当时(当不满足该条件时，向补充系数为0的高次项来扩大使其满足该条件)，将其化为两个多项式则有进而也就是说，要求在个不同点处的值，只需要求与在个不同点处的值，由于，可对与重复进行上述过程，最终经过步后得到个函数之后回推得到的点值表示，上述过程就是快速傅里叶变换的过程，复杂度为即.当然，还需要对进行同样的变换.3. 计算的点值表示点值表示的优点是可以快速地求出两个选取了相同点值的多项式的乘积，例如多项式与多项式的乘积只需要的复杂度即可求得.4. 将转化为系数表示下面以为例，讲解如何将多项式从点值表示转化为系数表示，此过程又称多项式的插值.将的点值表示写成矩阵形式即。
