高等数学---映射与函数
- 格式:ppt
- 大小:1.71 MB
- 文档页数:52




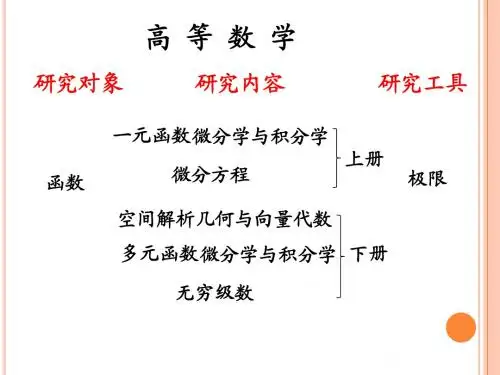
大一高数知识点映射与函数高等数学是大多数理工科专业大一必修的一门课程,其中包含了许多重要的数学知识点。
在这篇文章中,我们将重点讨论高数中的映射与函数。
一、映射的概念与性质映射是数学上非常重要的概念,它描述了元素之间的对应关系。
在集合论中,我们将一个元素从一个集合映射到另一个集合,这两个集合可以是相同的,也可以是不同的。
映射一般用函数符号f(x) 表示,其中 x 是原集合的元素,f(x) 是它在目标集合中的对应元素。
映射具有以下性质:1. 单射:若 f(x1) = f(x2),则 x1 = x2。
即不同的元素在映射中有不同的对应元素。
2. 满射:若对于任意的 y ∈目标集合,都存在 x ∈原集合,使得 f(x) = y。
即每一个元素都有对应的映射元素。
3. 一一映射:即又是单射又是满射的映射。
二、函数的定义与性质函数是映射的一种特殊形式,它在数学和其他学科中都有着广泛的应用。
函数的定义比较简洁,它是一种特殊的映射,其中原集合只能有一个元素对应到目标集合中的一个元素。
函数具有以下性质:1. 定义域和值域:函数的定义域是指输入变量的取值范围,值域是指函数输出的取值范围。
2. 奇偶性:函数 f(x) 的奇偶性取决于 f(-x) = f(x) 或 f(-x) = -f(x) 是否成立。
3. 单调性:函数在定义域上的增减状况,可以分为递增、递减或保持不变。
4. 极值与最值:函数在定义域的某一点或某一区间上取得的最大值或最小值。
5. 对称性:函数是否具有关于某个轴的对称性。
三、常见的函数类型在高数课程中,我们学习了许多常见的函数类型。
下面是其中一些重要的函数:1. 幂函数:y = x^n,其中 n 是正整数。
2. 指数函数:y = a^x,其中 a 是正实数且不等于 1。
3. 对数函数:y = log_a(x),其中 a 是正实数且不等于 1。
4. 三角函数:包括正弦函数、余弦函数和正切函数等。
5. 反三角函数:包括反正弦函数、反余弦函数和反正切函数等。


第一章函数与极限第一节映射与函数一、集合一般的所谓集合(简称集)是指具有某种性质的事物的从总体,组成这个集合的事物称为该集合的元素(简称元)。
二、集合的运算集合的基本运算有:并、交、差。
并A∪B=﹛x│x∈A或x∈B﹜交差A\B=﹛x│x∈A且x¢B﹜四项法则(1)交换律(2)结合律(3)分配律(4)对偶律(A∪B)C =A C∪B C注:在两个集合之间还可以定义直积或笛卡儿乘积。
设A、B是任意两个集合,在集合A 中任取一个元素x,在集合B中任取一个元素y,组成一个有序对(x,y)把这样的有序对作为新的元素,它们全体组成的集合称为集合A与集合B的直积,记A×B,既A×B=﹛﹙x,y﹚│x∈A且y∈B﹜3、区间和邻域二、映射概念定义设X、Y是两个非空集合,如果存在一个法则f,使得对X中每一个元素 x,按法则f,在Y中有唯一确定的元素y与之相对应,则称f为从X到Yf :X Y三、函数1、定义设数集D属于R,则称映射f:D R为定义在D上的函数,通常简记为y=f(x),x ∈D其中x 成为自变量,y成为因变量,D成为定义域,记作D f,既D f=D.2、几种特性:有界性单调性奇偶性周期性3、反函数与复合函数4、函数的运算和(差)积商5、初等函数幂函数:y=x a指数函数对数函数三角函数反三角函数双曲正弦 sh x=(e x-e -x)/2双曲余弦 ch x= (e x+e -x)/2双曲正切 th x= (e x-e -x)/ (e x-e -x)第二节数列的极限定义设{x n}为一数列,如果存在常数a,对于任意给定的正数µ (不论它多么小),总存在正整数N,使得 n﹥N时,不等式│x n │<µ都成立,那么就称常数a是数列{x n}的极限,或者称数列{x n}收敛于a,记为X a (n ∞)二、收敛数列的性质定理 1 (极限的唯一性)如果数列{ x n }收敛,那么他的极限唯一。




第1章函数与极限1.1 复习笔记一、映射与函数1.集合(1)集合概念集合(简称集)是指具有某种特定性质的事物的总体,组成这个集合的事物称为该集合的元素(简称元)。
常用大写拉丁字母A,B,C,…表示集合,用小写拉丁字母a,b,c,…表示集合的元素。
如果a是集合A的元素,就说a属于A,记作a∈A;如果a不是集合A的元素,就说a不属于A,记作a A。
一个集合,若它只含有有限个元素,则称为有限集;不是有限集的集合称为无限集。
(2)表示集合的方法通常有以下两种:①列举法,就是把集合的全体元素一一列举出来表示;②描述法,若集合M是由具有某种性质P的元素x的全体所组成的,就可表示成M={x|具有性质P}。
(3)常见的集合①空集,指不包含任何元素的集合,记为φ;②非负整数集,全体非负整数即自然数的集合,记作N,即N={0,1,2,…,n,…};③正整数集,全体正整数的集合,记作,即={1,2,3,…,n,…};④整数集,全体整数的集合,记作Z,即Z={…,-n,…,-2,-1,0,1,2,…,n,…};⑤有理数集,全体有理数的集合,记作Q,即Q={∈z,q∈且P与q互质};⑥实数集,全体实数的集合,记作R,R为排除数0的实数集,为全体正实数的集合。
(4)集合的关系①包含关系设A、B是两个集合,如果集合A的元素都是集合B的元素,则称A是B的子集,记作A B(读作A包含于B)或B A(读作B包含A)。
规定空集φ是任何集合A的子集,即φA。
若且,则称A是B的真子集,记作(读作A真包含于B)。
②等价关系若集合A与集合B互为子集,即A B且B A,则称集合A与集合B相等,记作A=B。
(5)集合的运算①并、交、差a.并集设A、B是两个集合,由所有属于A或者属于B的元素组成的集合,称为A与B的并集(简称并),记作,即。
b.交集由所有既属于A又属于B的元素组成的集合,称为A与B的交集(简称交),记作,即。
c.差集由所有属于A而不属于B的元素组成的集合,称为A与B的差集(简称差),记作A\B,即。
高数映射与函数例题高等数学中的映射与函数是重要的概念。
映射是指将一个集合中的元素对应到另一个集合中的元素的规则。
函数是一种特殊的映射,它满足每个自变量只有唯一的因变量对应。
下面我将给出一些关于映射与函数的例题,以帮助你更好地理解这个概念。
例题1,给定集合A={1, 2, 3, 4},集合B={a, b, c, d},写出一个映射f:A→B的规则。
解答,可以将每个元素1、2、3、4映射到集合B中的元素a、b、c、d。
例如,可以规定f(1)=a,f(2)=b,f(3)=c,f(4)=d。
例题2,已知函数f(x) = 2x + 1,求f(3)的值。
解答,将x=3代入函数f(x)中,得到f(3) = 2(3) + 1 = 7。
所以f(3)的值为7。
例题3,已知函数g(x) = x^2 + 3x,求g(-2)的值。
解答,将x=-2代入函数g(x)中,得到g(-2) = (-2)^2 + 3(-2) = 4 6 = -2。
所以g(-2)的值为-2。
例题4,已知函数h(x) = √x,求h(9)的值。
解答,将x=9代入函数h(x)中,得到h(9) = √9 = 3。
所以h(9)的值为3。
例题5,已知函数k(x) = |x|,求k(-5)的值。
解答,将x=-5代入函数k(x)中,得到k(-5) = |-5| = 5。
所以k(-5)的值为5。
通过以上例题,我们可以看到映射与函数的概念和运算方法。
映射是将一个集合中的元素对应到另一个集合中的元素,而函数是一种特殊的映射,满足每个自变量只有唯一的因变量对应。
在求函数值时,我们将给定的自变量代入函数表达式中,计算得到对应的因变量值。
希望以上例题能够帮助你理解映射与函数的概念和运算方法。
如果还有其他问题,请随时提问。