曲面立体截切例题
- 格式:ppt
- 大小:1.02 MB
- 文档页数:13

曲面切除练习题在解析几何中,曲面切除是一个重要的概念。
它是指通过一条曲线将一个曲面分为两个部分,其中一个部分是通过将曲面上的点与曲线相连而得到的封闭曲面。
曲面切除问题对于数学学习者来说是一项基本练习。
在本篇文章中,我们将通过一些练习题来加深对曲面切除的理解。
练习题一:曲面切除已知曲面S的方程为:\[f(x, y, z) = 0\]其中,f(x, y, z)为连续函数。
设曲线C的参数方程为:\[\begin{cases}x = x(t)\\y = y(t)\\z = z(t)\end{cases}\]其中,t的取值范围为[a, b]。
试证明:通过曲线C将曲面S切除的两个部分是封闭曲面。
解答:我们首先需要证明通过曲线C将曲面S切除的两个部分是曲面。
设曲线C上任意一点的参数为t,其对应的坐标为(x, y, z)。
由曲线C的参数方程可知,曲线C上的点满足方程组:\[\begin{cases}x = x(t)\\y = y(t)\\z = z(t)\end{cases}\]在曲线C上,将方程f(x, y, z) = 0代入上述方程组中,得到:\[f(x(t), y(t), z(t)) = 0\]因此,曲线C上的点也满足曲面S的方程。
由此可知,通过曲线C将曲面S切除的两个部分分别满足曲面S的方程,因此它们都是曲面。
其次,我们需要证明通过曲线C将曲面S切除的两个部分是封闭曲面。
设曲线C有两个参数方程:\[\begin{cases}x = x_1(t)\\y = y_1(t)\\z = z_1(t)\end{cases}\]\[\begin{cases}x = x_2(t)\\y = y_2(t)\\z = z_2(t)\end{cases}\]其中,t的取值范围分别为[a, b]和[c, d]。
我们分别考虑曲线C上两个参数方程对应的点序列{x_1(t), y_1(t), z_1(t)}和{x_2(t), y_2(t), z_2(t)}。
百度文库11-1 标注下列尺寸(尺寸数值由图中量取整数)1. 补全尺寸数字和箭头。
60°51φ3. 标注下列小间距尺寸。
332. 标注直径和半径尺寸。
1-4 比例,尺寸注法,斜度和锥度。
1. 参照所示图形,用1∶4在指定位置处画出图形,并标注尺寸。
1∶42002. 参照所示图形,用1∶1在指定位置处4.尺寸注法改错,将改正后的尺寸标注在右边空白图上。
R1550503. 参照所示图形,用1∶2在指定位置处画出图形,并标注尺寸。
09°18φ 241φ90°1φ2φ1φ5. 在下面图形上用1∶1度量后标注尺寸(取整数)2422.已知点A在H面之上20,点B在V面之前15,点C在V面上,点D在H面上,点E在投影轴上,补全诸点的两面投影。
第二章投影法基础3.已知点B在点A的左方15,前方10,上方5,又知点C与点B同高,且其坐标X=Y=Z,请作出点B和点C的投影。
4.判断下列各对重影点的相对位置,并填空。
1)点A在点B的正上方m2m22)点D在点C的正后方m2m22-1 点的投影。
1.按照立体图作诸点的三面投影3百度文库42.按已知条件画出下列直线的三投影1)画水平线 AB ,距 H 面20mm 与, V 面 成30°角,实长 25mm 。
2)画侧平线 EF ,距 W 面20mm ,与V 面 成30°夹角,实长 25mm 。
3. 分别在图( a ).(b ).(c ) 中,由点A 作直线AB 与CD 相交,交点 B距离V 面25mm 。
4. 根据轴测图,在三视图中标出线段 AB 和CD 的三投影 (点的三投影用小写字母标出) 并填写它们的名称和对各投影面的相对位置。
AB 是 正 平 线; CD 是 侧垂线。
AB: ∥ V,H, ∠ W ∠ 。
CD: V, ∥ H2-2 直线的投影 ( 一) 。
1. 判断下列直线对投影面的相对位置,并填写名称。
AB 是正 平线; EF 是侧平线; CD是 侧 垂 线; KM 是正垂线;百度文库2-2 直线的投影 ( 二)2. 已知线段AB 为正平线,C 为该线段上的一点 ,根据给出的投影 ,画出线段AB 和点C 的 水平投影和侧面投影。

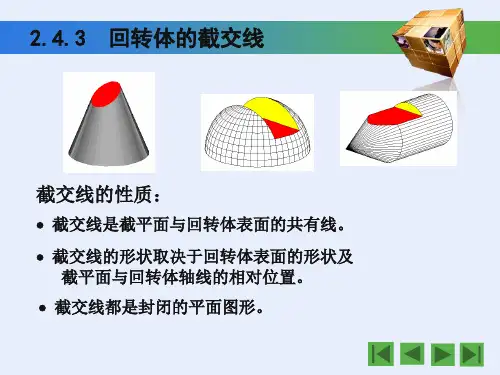
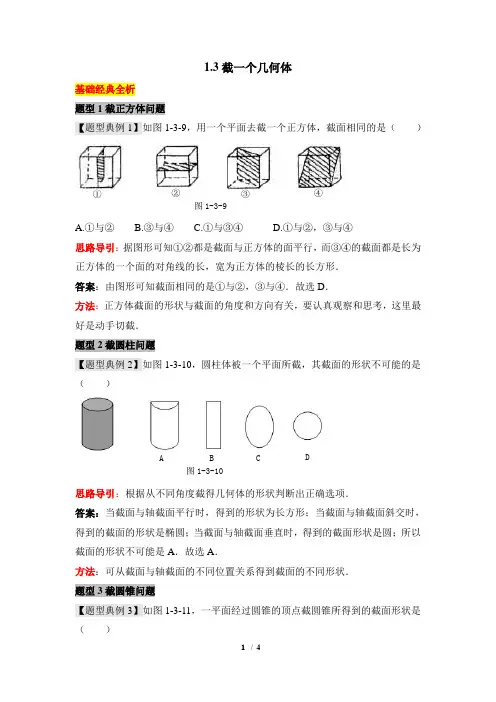
1.3截一个几何体基础经典全析题型1截正方体问题【题型典例1】如图1-3-9,用一个平面去截一个正方体,截面相同的是( )A.①与②B.③与④C.①与③④D.①与②,③与④思路导引:据图形可知①②都是截面与正方体的面平行,而③④的截面都是长为正方体的一个面的对角线的长,宽为正方体的棱长的长方形.答案:由图形可知截面相同的是①与②,③与④.故选D .方法:正方体截面的形状与截面的角度和方向有关,要认真观察和思考,这里最好是动手切截.题型2截圆柱问题【题型典例2】如图1-3-10,圆柱体被一个平面所截,其截面的形状不可能的是( )思路导引:根据从不同角度截得几何体的形状判断出正确选项.答案:当截面与轴截面平行时,得到的形状为长方形;当截面与轴截面斜交时,得到的截面的形状是椭圆;当截面与轴截面垂直时,得到的截面形状是圆;所以截面的形状不可能是A .故选A .方法:可从截面与轴截面的不同位置关系得到截面的不同形状.题型3截圆锥问题【题型典例3】如图1-3-11,一平面经过圆锥的顶点截圆锥所得到的截面形状是( )A BD C 图1-3-10 图1-3-9 ① ②③ ④思路导引:经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线,由图可知经过圆锥顶点的平面截圆锥所得的截面应该是个等腰三角形.答案:经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线,由图可知经过圆锥顶点的平面截圆锥所得的截面应该是个等腰三角形,故选B .方法:判断几何体的截面,关键要理解面与面相交得到线.题型4由截面判断几何体的形状【题型典例4】用一个平面截一个几何体,所截出的面出现了如图1-3-12所示的四种形式,试猜想,该几何体可能是 .思路导引:根据当截面的角度和方向不同时,截面不相同可判断几何体的形状. 答案:圆柱.平面倾斜竖截圆柱侧面和底面截圆柱截得到图①;平面倾斜圆柱底面截圆柱截得到椭圆;平面竖截圆柱得到长方形;平面平行圆柱底面截圆柱可以得到一个圆.故该几何体可能是圆柱.方法:由截面①②④可以推断几何体不是多面体,可能是圆柱、圆锥或圆台,由截面③可以推断该几何体可能是圆柱.综合创新探究题型5判断截后剩余图形的顶点数、棱数、面数【题型典例5】如图1-3-13,一正方体截去一角后,剩下的几何体有____个面,____条棱( )① ② ③④ 图1-3-12 A B CD图1-3-11 图1-3-13A .6,14 B.7,14 C.7,15 D.6,15思路导引:由图可知:截取一角后,剩下的几何体多了一个面,多了3条棱,即可求得.答案:截取一角后,剩下的几何体多了一个面,多了3条棱,即剩下的几何体由7个面,15条棱,故选C .方法:本题结合截面来判断多面体的顶点数、棱数、面数,这里一般可利用欧拉公式.题型6复杂的正方体的切截问题【题型典例6】如图1-3-14,是正方体被分割后的一部分,它的另一部分是( )思路导引:解答此类问题要从正方体分割后的一部分入手来观察分析,我们会发现截口呈“F”形,因此只要在四个选项中寻找相应的“F”即可.答案:B方法:解决正方体的切截问题,应利用认知的角度来感知三维世界的“空间”,最好是动手制作切截模型来验证.题型7截面知识在生产、生活中的应用【题型典例7】某车间要切割一些外形是长方体的物体,但该种物体的内部构造不详.于是工人师傅决定用一组水平的平面切截这个物体,得到了一组(自下而上)的截面,截面形状如图所示1-3-15,这个长方体的内部构造可能是什么?思路导引:通过观察可以发现:在正方体内部的圆自下而上由大圆逐渐变成小圆和点.答案:这个长方体的内部构造为:长方体中间有一圆锥状空洞.图1-3-14 A B D C 图1-3-15方法:由截面形状去想象几何体与给一个几何体想象它的截面是一个互逆的思维过程,要根据所给截面形状仔细分析,展开想象.备战中考用一个平面去截一个几何体后判断截面的形状是本节的考点,但中考中考查的量不大,主要目的是考查同学们的空间想象能力,题型一般以填空题、选择题为主,分值为3~6分,难度较小.考法1几何体的切截问题中考典例1用一个平面去截一个几何体,不能截得三角形截面的几何体是()A.圆柱 B.圆锥 C.三棱柱 D.正方形思路导引:看所给选项的截面能否得到三角形即可.答案:A选项中圆柱的截面可能是圆,长方形,符合题意;B选项中圆锥的截面可能是圆,三角形,不符合题意;C选项中三棱柱的截面可能是三角形,长方形,不符合题意;D选项中正方体的截面可能是三角形,或四边形,或五边形,或六边形,不符合题意.故选A.点拨:本题考查常见几何体的截面的形状,注意正方体的截面经过几个面就可得到几边形.变式练习1用平面去截下列几何体,截面的形状不可能是圆的几何体是()A.球 B.圆锥 C.圆柱 D.正方体思路导引:根据圆锥、圆柱、球、正方体的形状特点判断即可.答案:正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.故选D.。

教案首页
及时间分配、备注活动
教学内容
组织教学、
复习(2分
钟)
习题练习和
讲解(82分
钟)
1、根据复杂曲面立体图,补画视图中缺漏的图线:
2、根据复杂曲面立体图,画三视图:
(1)
及时间分配、备注活动
教学内容
习题练习和
讲解(82分
钟)
(2)
及时间分配、备注活动
教学内容
习题练习和
讲解(82分
钟)
3、补全接头的正面投影和水平投影。
及时间分配、备注活动
教学内容
习题练习和讲解(82分钟)二:参照立体图,完成带切口曲面立体的第三投影:1、
3、
及时间分配、备注活动
教学内容
习题练习和
讲解(82分
钟)
三、参照立体图,分析
下列各图的截交线,并补画视图:
3、
及时间分配、备注活动
教学内容
习题练习和讲解(82分钟)
总结易错处(5分钟)布置作业(1分钟)4、
总结
作业:
习题册相关习题。
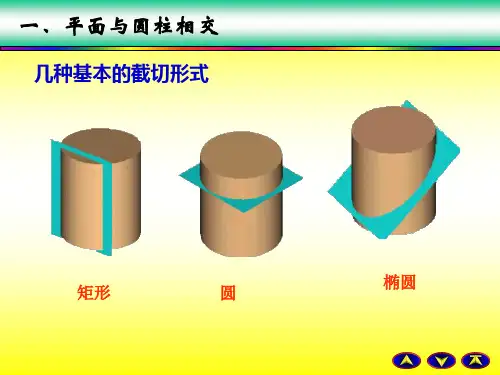
第一节、平面与圆柱体相交平面与圆柱体相交,截交线的形状取决于截平面与圆柱轴线的相对位置。
平面截切圆柱体截交线的形式有三种。
例:已知斜切圆柱体的主视图和俯视图,求左视图。
解:分析——圆柱的轴线是铅垂线,截平面为正垂面且与圆柱轴线倾斜,斜切圆柱体的截交线为椭圆。
截交线的正面投影积聚为直线,水平投影积聚在圆周上,侧面投影为椭圆。
作图步骤:(1)求特殊点截交线最左素线上的点Ⅰ和最右素线上的点Ⅱ分别是截交线的最低点和最高点。
截交线最前点Ⅲ和最后点Ⅳ分别是最前素线和最后素线与截平面的交点。
作出Ⅰ、Ⅱ、Ⅲ、Ⅳ的正面投影1'、2'、3'、4'和水平投影1、2、3、4,根据从属关系求出1"、2"、3"、4"。
(2)求一般点从正面投影上选取a'、b'、c'、d'四点,然后作OX轴的垂线求得a、b、c、d,根据点的投影规律求出侧面投影a"、b"、c"、d"。
(3)按截交线的顺序,光滑地连接各点的侧面投影。
已知条件求特殊点求一般点例:求开槽圆柱的左视图。
解:分析——圆柱体上部的槽是由三个截平面形成的,左右对称的两个截平面是平行于圆柱轴线的侧平面,它们与圆柱面的截交线均为两条直素线,与上底面的截交线为正垂线。
另一个截平面是垂直于圆柱轴线的水平面,它与圆柱面的截交线为两段圆弧。
三个截平面间产生了两条交线,均为正垂线。
作图——在水平投影上和正面投影上找出特殊点1、2、3、4、5、6和1'、2'、3'、4'、5'、6'根据点的投影规律作出1"、2"、3"、4"、5"、6",按顺序依次连接各点。
判别可见性:截平面交线的侧面投影为不可见,应画成虚线。
已知条件作图过程例:已知圆柱截断体的正面和侧面投影,求水平投影。