椭圆中的焦点弦问题

焦点弦公式引言焦点弦公式是解决椭圆、双曲线和抛物线相关问题的重要公式之一。

它通过求取曲线的焦点坐标和弦长以及焦点与弦的垂直距离的关系，为解决相关问题提供了便利。

本文将详细介绍焦点弦公式的推导过程以及应用场景，并给出一些实际问题的例子来帮助读者更好地理解焦点弦公式。

焦点弦公式的推导焦点弦公式的推导涉及到椭圆、双曲线和抛物线三种常见曲线的方程及其性质。

在这里，我们以椭圆为例进行推导。

椭圆的定义和性质椭圆是一个平面上所有点到两个焦点的距离之和等于常数的轨迹。

设椭圆的焦点坐标分别为F1和F2，椭圆的长轴和短轴分别为2a和2b，则椭圆的方程可以表示为：(x^2/a^2) + (y^2/b^2) = 1椭圆的焦点与直径的关系可以表示为：2ae = d其中e为离心率，d为焦点之间的距离。

焦点弦公式的推导过程我们考虑椭圆上一点P(x,y)到焦点F1的距离为r1，到焦点F2的距离为r2，焦点与弦的垂直距离为h，弦的长度为2c。

根据椭圆的定义，我们可以得到以下两个方程：r1 + r2 = 2ar1 - r2 = 2h通过解以上方程组，我们可以求解出r1和r2的值：r1 = a + hr2 = a - h根据勾股定理，可以得到焦点弦公式：c^2 = r1^2 - r2^2 = (a + h)^2 - (a - h)^2 = 4ah焦点弦公式的应用焦点弦公式在解决椭圆、双曲线和抛物线相关问题中有广泛的应用。

下面我们将介绍一些实际问题，展示焦点弦公式的具体应用。

问题一：求解椭圆的焦点坐标已知椭圆的方程为(x^2/4) + (y^2/9) = 1，求解焦点坐标。

根据椭圆的方程，可以得到a^2 = 4和b^2 = 9，因此a = 2，b = 3。

根据焦点与直径的关系，可以求得ae = 2ae = 4，因此e = 2，焦点之间的距离为d = 2ae = 4。

由于焦点到直径的距离等于焦点与弦的垂直距离，可以得到焦点与弦的垂直距离h = d/2 = 2。

椭圆的焦点弦长公式的四种推导方法及其应用摘要：直线与椭圆相交时的弦长问题，可以用万能的弦长公式解决即12AB x -或者12AB y -，而有一种特殊的弦是过焦点的弦，它的弦长有专门的公式：22222cos ab AB a c θ=-，如果记住公式，可以给我们解题带来方便.下面我们用万能弦长公式，余弦定理，焦半径公式，仿射性四种方法来推导椭圆的焦点弦长公式，这几种方法涉及到很多思想，最后举例说明其应用.解法一：根据弦长公式直接带入解决.题：设椭圆方程为12222=+by a x ，左右焦点分别为12(,0),(,0)F c F c -，直线l 过椭圆的右焦点2F 交椭圆于1122(,),(,)A x y B x y 两点，求弦长AB .椭圆方程12222=+by a x 可化为0222222=-+b a y a x b ……①，直线l 过右焦点，则可以假设直线为：x my c =+(斜率不存在即为0m =时)，代入①得：222222222()20b m a y mcb y b c a b +++-=，整理得，222224()20b m a y mcb y b ++-=∴2412122222222,mcb b y y y y b m a b m a +=-=-++，∴12AB y -==∴()2222221ab AB m b m a=++ （1）若直线l 的倾斜角为θ，且不为90,则1tan m θ=，则有： ()2222222222221111tan tan ab ab AB m b m a b a θθ⎛⎫=+=+ ⎪+⎝⎭+,由正切化为余弦，得到最后的焦点弦长公式为22222cos ab AB a c θ=-……②. （2）若=90θ，则0m =，带入()2222221ab AB m b m a =++,得通径长为22b a ，同样满足②式.并且由()222232222222222222222222()222()2()21=22ab a b m a a ab a a b a a b b AB m a a b m a b m a b m a a a +-+--=+=-≥-=+++,当且仅当0=m 即斜率不存在的时候，过焦点弦长最短为a b 22，故可知通径是最短的焦点弦，.综上，焦点弦长公式为22222cos ab AB a c θ=-.解法二：根据余弦定理解决题：设椭圆方程为12222=+by a x ，左右焦点分别为12(,0),(,0)F c F c -，直线l 过椭圆的右焦点2F 交椭圆于1122(,),(,)A x y B x y 两点，求弦长AB .解：如右图所示，连结11,F A F B ，设22=,F A x F B y =，假设直线的倾斜角为θ，则由椭圆定义可得11=2,2F A a x F B a y -=-，在12AF F ∆中，由余弦定理得222(2)(2)cos()4c x a x cx πθ+---=，化简可得2cos b x a c θ=-，在12BF F ∆中，由余弦定理同理可得2cos b y a c θ=+，则弦长2222222=cos cos cos b b ab AB x y a c a c a c θθθ=+=+-+-.解法三：利用焦半径公式解决题：设椭圆方程为12222=+by a x ，左右焦点分别为12(,0),(,0)F c F c -，直线l 过椭圆的右焦点2F 交椭圆于1122(,),(,)A x y B x y 两点，求弦长AB .解：由解法一知22212121222222222=()22m cb a cx x my c my c m y y c c b m a b m a ++++=++=-+=++.由椭圆的第二定义可得焦半径公式，那么2122,F A a ex F B a ex =-=-故222221212222222222(1)=2()ab m ab ab m AB a ex a ex a e x x b m a b m a ++-+-=-+==++后面分析同解法一.解法四：利用仿射性解决题：设椭圆方程为12222=+by a x ，左右焦点分别为12(,0),(,0)F c F c -，直线l 过椭圆的右焦点2F 交椭圆于1122(,),(,)A x y B x y 两点，求弦长AB .解：利用仿射性，可做如下变换''x xa y yb =⎧⎪⎨=⎪⎩，则原椭圆变为222(')(')x y a +=，这是一个以原点为圆心，a 为半径的圆.假设原直线的斜率为k ，则变换后斜率为ak b.椭圆中弦长212=1AB k x x +-，经过变换后变为212''1()a A B k x x b=+-，带入，得变换前后弦长关系为22221=''b k AB A B b a k++……③而我们知道圆的弦长可以用垂径定理求得.如图所示，假设直线为()ay k x c b=-，圆心到直线的距离为21()a kc bd a k b=+，根据半径为a ，勾股定理求得弦长为222222222()(1)''=221()akc a b k b A B a ak b a k b+-=++，将此结果带入③中，得222222222222222222211(1)2(1)=''=2=b k b k a b k ab k AB A B b a k b a k b a k b a k++++++++，由tan k θ=，带入得 22222cos ab AB a c θ=-.上面我们分别用了四种不同的方法，求出了椭圆中过焦点的弦长公式为：22222cos ab AB a c θ=-，记住这个公式，可以帮助我们快速解决一些题目，下面我们举例说明.例1已知椭圆2212521x y +=的直线交椭圆于,A B 两点，求AB . 分析：如果直接用弦长公式解决，因为有根号，特别繁琐，利用公式则迎刃而解.解：由题，225,21,4=3a b c πθ===，,带入22222cos ab AB a c θ=-得=10AB . 例2已知点3(1,)2P -在椭圆C ：22221(0)x y a b a b +=>>上，过椭圆C 的右焦点2(1,0)F 的直线l 与椭圆C 交于,M N 两点. （1）求椭圆的标准方程；（2）若AB 是椭圆C 经过原点O 的弦，且MNAB ，2ABW MN=,试判断W 是否为定值？若是定值，求出这个定值，若不是，说明理由.分析：因为l 过焦点，故弦长可以用过焦点的弦长公式解决，显得十分简洁简单. 解：（1）由题知1c =，将点P 带入得221914a b+=，又222a b c =+，解得224,3a b ==，故椭圆方程为22143x y +=. （2）假设(,)A m n，则AB =，设倾斜角为θ，则cos θ=，根据过焦点的弦长公式则2222222222221234cos 12()4abm n MN m a c m n m n θ+===-+-+，故222=443ABm n W MN =+（）=4. 例3如图，已知椭圆22143x y +=的左右焦点为12,F F ，过2F 的直线1l 交椭圆于,A C 两点，过1F 的直线2l 交椭圆于,B D 两点，12,l l 交于点P (P 在x 轴下方)，且1234F PF π∠=，求四边形ABCD 的面积的最大值.分析：注意到以原点为圆心，半焦距为半径的圆与椭圆没有交点，故形成1234F PF π∠=的点P 在圆内，先可以用焦点弦长公式表示出面积，再利用换元求出其最大值.解：假设1l 的倾斜角为θ,则2l 的倾斜角为3+4πθ，由椭圆的焦点弦长公式得：2124cos AC θ=-, 2124cos ()4BD πθ=--，221221212=2244cos 4cos ()4S AC BD πθθ⋅⋅⋅=⋅⋅---, 设22()(4cos )(4cos ())4f πθθθ=---71714971(cos 2)(sin 2)sin 2+cos 2+sin 42222448θθθθθ=--=-（） 设sin 2cos 2(2,2)t t θθ⎡⎤+=∈-⎣⎦， 则2sin 41t θ=-,带入得24971()+(1)448f t t t =-- 即21797()848f t t t =-+ min 99142()8f t -=,此时2t =， 即sin 2cos 22θθ+=，得到=8πθ.综上，四边形ABCD 的最大值为2882=5.1499142S ≈-.此时=8πθ，得到2l 的倾斜角为78π,刚好两直线关于y 轴对称，如右图所示.。

椭圆中焦点弦长定比问题是一个常见的几何问题，涉及到椭圆的性质以及焦点和弦长的关系。

假设椭圆的标准方程为 x^2/a^2 + y^2/b^2 = 1，其中 a和b是椭圆的半长轴和半短轴，c 是焦点到原点的距离，满足 c^2 = a^2 - b^2。

焦点弦是指通过椭圆两个焦点的线段，其长度记为2p。

在椭圆中，焦点弦长与椭圆的长轴和短轴之间存在定比关系。

这个定比关系可以通过椭圆的性质推导出来。

根据椭圆的定义，任意一点P到椭圆两个焦点的距离之和等于椭圆的长轴长，即 |PF1| + |PF2| = 2a。

当点P在椭圆上时，|PF1|和|PF2|分别表示点P到两个焦点的距离。

由于焦点弦通过两个焦点，因此焦点弦的长度2p等于 |PF1| + |PF2|。

所以，焦点弦长2p与椭圆的长轴长2a之间存在定比关系，即 2p = 2a。

这个定比关系表明，无论焦点弦在椭圆上的位置如何变化，其长度始终等于椭圆的长轴长。

焦点弦长定比问题在椭圆几何中具有重要的应用价值，可以用于解决与椭圆相关的其他问题，如求解椭圆的离心率、判断点是否在椭圆上等。

以上，是椭圆中焦点弦长定比问题的基本解释和推导。

椭圆顶点弦和焦点弦的性质及运用椭圆顶点弦和焦点弦是几何学里关于椭圆的概念，常被用于各种应用，从精确的科学计算到日常生活的活动。

因此，理解椭圆顶点弦和焦点弦的性质及运用，对于几何学的学习者尤其重要。

首先，让我们了解什么是椭圆顶点弦和焦点弦。

根据椭圆的定义，椭圆是一种特殊的抛物线，其中两个焦点（也称作焦点）和一组顶点（也叫顶点）组成了一个闭合的曲线。

椭圆顶点弦是从一个顶点出发，连接到另一个顶点的线段，而焦点弦是从一个焦点出发，连接到另一个焦点的线段。

当一个椭圆接近它的长轴时，椭圆顶点弦会变得很长，而焦点弦会变得很短。

椭圆顶点弦和焦点弦的性质有很多。

首先，它们的长度都是定值，这一性质的特殊，使得它们可以用于计算距离和角度。

其次，在椭圆的任意两个顶点之间，顶点弦的长度大于焦点弦的长度，这一性质可以用于几何证明中的椭圆周长的求解。

此外，两个平行的顶点弦（也就是两个顶点是同一条直线上的）等长，两个垂直的顶点弦也等长，而且都大概等于椭圆的短轴长度。

椭圆顶点弦和焦点弦也存在一些重要的运用。

它们可以用来求解几何形体的一些参数。

例如，如果已知两个顶点的坐标，则可以通过求解椭圆顶点弦的长度来计算椭圆的长轴长度。

此外，它们还可以用来描述一些物理现象，如对波的反射。

这些现象可以用来解释太阳能系统中的热辐射，以及天文学中的光度降低等。

另外，椭圆顶点弦和焦点弦在工程计算中也有许多应用。

它们可以用来计算车辆经过曲线路段时的运动轨迹，以及火箭发射轨道计算等。

它们甚至可以用来求解旋转的机械系统的运动轨迹，例如螺旋桨的运动等。

总之，椭圆顶点弦和焦点弦是几何学中重要的概念。

它们的性质可以用来求解几何形体的参数，还可以用来描述一些物理现象，并拓展出许多工程计算应用。

理解椭圆顶点弦和焦点弦的性质及运用，对于几何学的学习者有着重要的意义。

圆锥曲线焦点弦的八大结论圆锥曲线是几何学中的一类重要的曲线，包括圆、椭圆、双曲线和抛物线。

在圆锥曲线的研究中，焦点和弦是两个重要的概念，它们之间有着许多有趣的关系。

本文将介绍圆锥曲线焦点弦的八大结论。

一、椭圆的焦点弦椭圆有两个焦点，分别为F1和F2。

对于任意一条经过椭圆两个焦点的弦AB，有以下结论：1. 弦中点M在线段F1F2上；2. 焦点到弦的距离之和等于弦长，即AF1 + BF2 = AB；3. 焦点到弦的距离之差等于弦段所在直线与椭圆长轴的距离之差，即AF1 - BF2 = PM - PN，其中P和N分别为弦AB的两个端点在椭圆上的垂足；4. 焦点到弦的距离之比等于弦段所在直线与椭圆焦点连线的斜率，即AF1/AF2 = MF/MG，其中M为弦中点，G为椭圆长轴的中点；5. 弦中点M到椭圆两个焦点的距离之差等于弦段所在直线与椭圆长轴的距离之差，即MF1 - MF2 = PM - PN；6. 弦端点P和N到椭圆两个焦点的距离之差相等，即PF1 - PF2 = NF1 - NF2；7. 椭圆的两个焦点到弦的距离之积等于椭圆长轴的平方减去弦长的平方，即AF1·BF2 = AC - AB，其中AC为椭圆长轴的长度；8. 弦段所在直线与椭圆中心连线的斜率等于椭圆长轴和短轴的比值，即PG/PM = b/a，其中a和b分别为椭圆长轴和短轴的长度。

二、双曲线的焦点弦双曲线有两个焦点，分别为F1和F2。

对于任意一条经过双曲线两个焦点的弦AB，有以下结论：1. 弦中点M在线段F1F2的延长线上；2. 焦点到弦的距离之差等于弦长，即AF1 - BF2 = AB；3. 焦点到弦的距离之和等于弦段所在直线与双曲线渐近线的距离之和，即AF1 + BF2 = PM + PN，其中P和N分别为弦AB的两个端点在双曲线上的垂足；4. 焦点到弦的距离之比等于弦段所在直线与双曲线渐近线的斜率，即AF1/AF2 = MF/MG，其中M为弦中点，G为双曲线渐近线的中点；5. 弦中点M到双曲线两个焦点的距离之和等于弦段所在直线与双曲线渐近线的距离之和，即MF1 + MF2 = PM + PN；6. 弦端点P和N到双曲线两个焦点的距离之差相等，即PF1 - PF2 = NF2 - NF1；7. 双曲线的两个焦点到弦的距离之积等于双曲线的常数c的平方减去弦长的平方，即AF1·BF2 = c - AB，其中c为双曲线的常数；8. 弦段所在直线与双曲线中心连线的斜率等于双曲线焦点之间的距离和双曲线渐近线的斜率之和的倒数，即PG/PM = (F1F2/c) + (c/PN)。

椭圆相互垂直的焦点弦倒数和全文共四篇示例，供读者参考第一篇示例：椭圆是一种常见的几何形状，是平面上一点到两个定点（焦点）的距离之和等于常数的所有点的集合。

椭圆在数学和物理学中有着广泛的应用，而它与焦点之间的关系更是数学家们的研究对象之一。

在椭圆中，焦点是椭圆的一个重要特征，它与椭圆上的所有点都有一定的关系。

如果把椭圆看作一个圆，那么焦点就是在圆上的两个点。

在椭圆中，焦点的位置是非常特殊的，它和椭圆的形状密切相关。

椭圆通常有两个焦点，我们可以将这两个焦点分为主焦点和副焦点。

主焦点是椭圆长轴上的两个焦点中距离较大的那个，而副焦点则是距离较小的那个。

焦点之间的距离是椭圆的一个重要特征，不同大小的焦点距离会导致椭圆形状的变化。

在研究椭圆时，数学家们发现了一个有趣的现象：椭圆的主焦点和副焦点之间的弦的倒数是一个常数。

这个常数被称为椭圆的焦点弦倒数和，是一个固定的数值，不随椭圆的形状而变化。

椭圆的焦点弦倒数和可以用数学公式来表示。

设椭圆的主焦点为F1（x1，y1），副焦点为F2（x2，y2），椭圆上任意一点P（x，y），则椭圆的焦点弦倒数和为：1/ PF1 + 1/ PF2 = 常数椭圆的焦点弦倒数和是一个有趣的数学性质，它揭示了椭圆的内在规律和结构。

这个性质在数学研究和实际应用中都具有重要的意义，能够帮助我们更深入地理解和应用椭圆这一几何形状。

第二篇示例：椭圆是一种重要的几何形状，由具有不同焦点和不同轴的两个焦点组成。

椭圆与一根通过其两个焦点的线段形成了两个相互垂直的焦点弦。

在本文中，我们将讨论椭圆相互垂直的焦点弦的倒数和。

让我们来回顾一下椭圆的定义。

椭圆是一个闭合曲线，其上所有点到两个焦点的距离之和等于一个常数的图形。

椭圆由一个水平轴和一个垂直轴组成，焦点位于水平轴上。

椭圆的形状由其长轴和短轴的长度决定。

让我们考虑一个简单的椭圆，其短轴长度为2，长轴长度为4。

这个椭圆的两个焦点分别为(-1,0)和(1,0)。

椭圆的焦半径和焦点弦2用焦半径的长度的范围解题知识点：设椭圆的焦半径为r ，则a-c≤r ≤a+c1.椭圆x 2a 2+y 2b 2=1(a >b >0) 的左、右焦点分别是F 1、F 2，若存在点M 使|MF 1|=3|MF 2|,则该椭圆离心率的取值范围是 .法一：用焦半径的范围r 1+r 2=2a,r 1=3r 2,2r 2=a,a-c≤a 2≤a+c,e≥12法二：用焦半径公式＋椭圆上点的坐标的范围a+ex =3(a-ex ),2ex =a ,x =a 2e ，又x ≤a , e≥12法三：用特殊位置＋椭圆离心率的意义当M 点是右顶点时，a+c =3(a-c ),4c =2a ,e =12 , 另外，当椭圆越来越扁时，必存在点M 使|MF 1|=3|MF 2|,所以e ≥122.已知椭圆C ：x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1(-c ,0),F 2(c ,0),若椭圆C 上存在一点P 使a sin∠PF1F2＝ c sin∠PF2F1,则该椭圆的离心率的取值范围为___________.【答案】)1,1- 法一：用焦半径公式＋椭圆上点的坐标的范围因为在12PF F ∆中,由正弦定理得211221sin sin PF PF PF F PF F = 则由已知,得1211a c PF PF =,即12aPF cPF = 设点00(,)x y 由焦点半径公式,得1020,PF a ex PF a ex =+=-则00()()a a ex c a ex +=-记得0()(1)()(1)a c a a e x e c a e e --==-+由椭圆的几何性质知0(1)(1)a e x a a e e ->->-+则,整理得2210,e e +->解得11(0,1)e e e <<∈或，又,故椭圆的离心率1,1)e ∈ 法二：用焦半径的范围由法一知12c PF PF a=由椭圆的定义知 212222222c a PF PF a PF PF a PF a c a+=+==+则即,由椭圆的几何性质知22222,,20,a PF a c a c c c a c a<+<++->+则既所以2210,e e +->以下同解析1.3.已知椭圆C ：x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ，直线x =a 2c 与x 轴的交点为A ，在椭圆上存在点P 满足线段AP 的垂直平分线过点F ，则椭圆离心率的取值范围是（ ）A ．10,2⎛⎤ ⎥⎝⎦B ．1,12⎡⎫⎪⎢⎣⎭C ．⎛ ⎝⎦D ．⎫⎪⎪⎣⎭【答案】B【详解】由题意，椭圆上存在点P ，使得线段AP 的垂直平分线过点F ，即F 点到P 点与A点的距离相等，即|PF |=|F A |，|F A |= 22,a b c c c-=又[,]PF a c a c ∈-+ 2[,]b a c a c c∴∈-+222ac c b ac c ∴-≤≤+ 222222ac c a c ac c a c ⎧-≤+∴⎨+≥-⎩22210210e e e e ⎧-+≥∴⎨+-≥⎩解得12e ≥或1e ≤-（舍）又1(0,1)[,1)2e e ∈∴∈4.已知椭圆x 24+y 2=1，F 1、F 2分别是椭圆的左、右焦点，点P 为椭圆上的任意一点，则1|PF1|+1|PF2|的取值范围为（ ）A ．[]1,2B． C．4⎤⎦ D ．[]1,4【答案】D 【详解】对于椭圆2214x y +=，2a =，1b =，c = 根据椭圆的定义可得1224PF PF a +==， 设1PF x =，则24PF x =-，且a c x a c -≤≤+，即22x ≤≤ 则()()[]221244241,4PF PF x x x x x ⋅=-=-+=--+∈， 所以，[]121212121141,4PF PF PF PF PF PF PF PF ++==∈⋅⋅.。

焦点弦的角度公式焦点弦的角度公式是解决焦点弦相关问题的重要工具。

焦点弦指的是一条通过椭圆焦点且与椭圆相交于两个点的线段。

焦点弦的角度公式可以用来计算焦点且已知椭圆上的两个点的角度。

本文将以焦点弦的角度公式为标题，详细介绍焦点弦的概念、角度公式的推导以及应用举例。

一、焦点弦的概念焦点弦是指一条通过椭圆焦点的线段，且与椭圆相交于两个点。

在椭圆中，焦点是特殊的点，具有重要的几何性质。

当焦点弦与椭圆相交时，可以利用焦点弦的角度公式计算焦点且已知椭圆上的两个点的角度。

二、焦点弦的角度公式的推导为了推导焦点弦的角度公式，我们先回顾一下椭圆的性质。

椭圆的焦点到椭圆上任意一点的距离之和是一个常数，这个常数称为椭圆的焦距。

设焦点到椭圆上的两个点的距离分别为d1和d2，焦距为2a，则有d1+d2=2a。

根据椭圆的性质，我们可以得到焦点弦的角度公式。

设焦点弦与椭圆相交于A、B两点，焦点为F。

首先，我们将焦点弦延长，使其与椭圆交于C点。

则有AC=BC，且AF=BF。

根据余弦定理，我们可以得到以下关系式：AC² = AF² + FC²BC² = BF² + FC²由于AC=BC，我们可以将上述两个关系式相等，得到：AF² + FC² = BF² + FC²将上述等式化简，得到：AF² = BF²进一步化简，我们可以得到：AF = BF由此可见，焦点弦的角度公式为：∠AFB = ∠BAF三、焦点弦角度公式的应用举例现在我们通过一个具体的例子来应用焦点弦的角度公式。

假设椭圆的焦点为F1和F2，椭圆上的两个点为A和B。

已知焦点到A的距离为d1，焦点到B的距离为d2，焦距为2a。

根据焦点弦的角度公式，我们可以得到∠AF1B = ∠BAF1和∠AF2B = ∠BAF2。

因此，我们可以利用已知的角度和距离计算其他未知量。

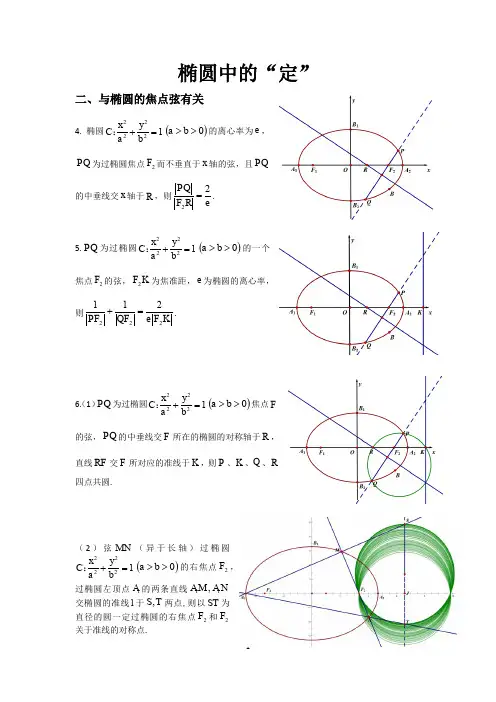
椭圆中的“定”二、与椭圆的焦点弦有关4. 椭圆12222=+by a x C ：()0>>b a 的离心率为e ，PQ 为过椭圆焦点2F 而不垂直于x 轴的弦，且PQ的中垂线交x 轴于R ，则22PQ F R e=. 5.PQ 为过椭圆12222=+by a x C ：()0>>b a 的一个焦点2F 的弦，2F K 为焦准距，e 为椭圆的离心率，则222112PF QF e F K+=.6.（1）PQ 为过椭圆12222=+by a x C ：()0>>b a 焦点F 的弦，PQ 的中垂线交F 所在的椭圆的对称轴于R ，直线RF 交F 所对应的准线于K ，则P 、K 、Q 、R 四点共圆.（2）弦MN （异于长轴）过椭圆12222=+by a x C ：()0>>b a 的右焦点2F ，过椭圆左顶点1A 的两条直线11,A M A N交椭圆的准线l 于,S T 两点,则以ST 为直径的圆一定过椭圆的右焦点2F 和2F 关于准线的对称点.（3）弦MN 过椭圆12222=+by a x C ：()0>>b a 的右焦点2F ，椭圆的准线l 交椭圆的对称轴于点D ,则22MDF NDF ∠=∠.（4）P 为椭圆12222=+by a x C ：()0>>b a 上任一点，2F 为椭圆右焦点，过P 作椭圆的切线交椭圆的右准线于点N ，则222ON PF b k k a=-.7.(1,2,3,)n n P Q n =为过圆锥曲线的一个焦点2F 的弦，n n P Q 的中垂线交2F 所在的曲线的对称轴于n R ，则过,,(1,2,3,)n n n P Q R n =的圆必交于同一点2,0a c ⎛⎫ ⎪⎝⎭.8. 弦AB （异于长轴）过椭圆12222=+b y a x C ：()0>>b a 的焦点，过B A ,两点分别作椭圆的两条切线交圆222x y a +=于,M M '两点，则（1）MM '是圆222x y a +=的一条直径，且四边形MM BA '为梯形；（2）角APB ∠为锐角；（3）若两切线的交点为P ，当点P 为2,0a c ⎛⎫ ⎪⎝⎭时，APB ∆的面积最小，其最小值为4b ac.9.在椭圆12222=+by a x C ：()0>>b a 通径（过焦点且垂直于焦点轴的弦）的延长线上任取一点()00,P x y 作椭圆两条切线12,PP PP ，则切点弦12PP ，x 轴和准线l 三线共点.10.直线l 是过椭圆12222=+b y a x C ：()0>>b a 上一点P 的切线，它与经过椭圆左顶点1A 的切线交于点N ，椭圆的左焦点F 和点N 的的连线FN 与左准线交于点M ，则椭圆的右顶点2A ，切点P 及点M 三点共线.11.直线l 是过椭圆12222=+by a x C ：()0>>b a 上一点P 的切线，它与经过椭圆右顶点2A 的切线交于点N ，椭圆的左焦点F 和点N 的的连线FN 与左准线交于点M ，则椭圆的左顶点1A ，切点P 及点M 三点共线.12.直线l 是过椭圆12222=+by a x C ：()0>>b a 上一点P 的切线，过该椭圆右的左焦点1F 作1F N l ⊥，且与椭圆的左准线交于点M ，则椭圆的中心O ，切点P 及点M 三点共线.、13. 如图，点F 是椭圆12222=+b y a x C ：()0>>b a 的右焦点，直线l 是椭圆的右准线，点P 在椭圆上且PF x ⊥轴，AB 是经过右焦点F的任一弦（不经过点P ），设直线AB 与直线l 相交于点M ，则2PA PB PM k k k +=.14. 过椭圆12222=+by a x C ：()0>>b a 的焦点(),0F c 作倾斜角为θ的直线，交椭圆于,A B 两点，则2221cos ep AB e θ=-（e 为离心率，p 为焦参数（通径长的一半））. 15. 弦AB 过椭圆12222=+by a x C ：()0>>b a 的焦点F ，且AF FB λ=（点A 位于点B 之上），则弦AB 所在直线的斜率()()()222110,11e k λλλλ+=-≠≠±-.。