高考数学竞赛圆锥曲线中与焦点弦相关的问题

专题01 圆锥曲线中的弦长问题一、单选题1．设椭圆长半轴长为a ，短半轴长为b ，半焦距为c ，则过焦点且垂直于长轴的弦长是（ ）A ．2b aB ．22c aC ．2c aD ．22b a2．已知椭圆22:12x C y +=，直线l 过椭圆C 的左焦点F 且交椭圆于A ，B 两点，AB 的中垂线交x 轴于M点，则2||||FM AB 的取值范围为（ ）A ．11,164⎛⎫⎪⎝⎭ B ．11,84⎡⎫⎪⎢⎣⎭C ．11,162⎛⎫⎪⎝⎭ D ．11,82⎡⎫⎪⎢⎣⎭3．过椭圆9x 2+25y 2=225的右焦点且倾斜角为45°的弦长AB 的长为（ ） A ．5B ．6C ．9017D ．74．椭圆()2222:10x y C a b a b+=>>的左、右焦点分别是1F 、2F ，斜率为12的直线l 过左焦点1F 且交C 于A ，B 两点，且2ABF 的内切圆的周长是2π，若椭圆C 的离心率为13,24e ⎡⎤∈⎢⎥⎣⎦，则线段AB 的长度的取值范围是（ ）A ．⎣B ．⎣C ．⎣⎦D ．⎣⎦二、多选题5．已知抛物线()220y px p =>的焦点为F ，过点F 的直线l 交抛物线于A 、B 两点，以线段AB 为直径的圆交y 轴于M 、N 两点，则（ ）A ．若抛物线上存在一点()2,E t 到焦点F 的距离等于3，则抛物线的方程为24y x =B ．若2AF BF =，则直线l 的斜率为C ．若直线l 43p AB =D ．设线段AB 的中点为P ，若点F 到抛物线准线的距离为2，则sin PMN ∠的最小值为12三、解答题6．如图，P 是直线:3l y x =+上一动点，过点P 且与l 垂直的直线l '交抛物线2:C y x =于A ，B 两点，点A 在P ，B 之间．（1）若l '过抛物线C 的焦点F ，求AB ；（2）求PA PB的最小值．7．已知椭圆22221x y a b+=（0a b >>）长轴长为短轴长的两倍，连结椭圆的四个顶点得到的菱形的面积为4，直线l 过点(,0)A a -，且与椭圆相交于另一点B ． （1）求椭圆的方程；（2）若线段AB l 的倾斜角． 8．已知直线l 经过抛物线26y x =的焦点F ，且与抛物线交于A 、B 两点. （1）若直线l 的倾斜角为60，求线段AB 的长； （2）若2AF =，求BF 的长.9．已知圆上224x y +=上任取一点P ，过点P 作y 轴的垂线段PQ ，垂足为Q ，当P 在圆上运动时，线段PQ 中点为M .（1）求点M 的轨迹方程；（2）若直线l 的方程为y ＝x －1，与点M 的轨迹交于A ，B 两点，求弦AB 的长.10．已知椭圆22:1(0)C a b a b+=>>的右焦点为F ，左、右顶点为A 、B ，3FA =，1FB =.（1）求椭圆C 的标准方程； （2）求直线12y x =+被椭圆C 截得的弦长. 11．已知直线:4380l x y --=与圆()()22:11M x y m ++-=相交. （1）求m 的取值范围；（2）若l 与M 相交所得弦长为8，求直线:40l x y '+-=与M 相交所得弦长.12．已知双曲线C 的标准方程为22136x y -=，12,F F 分别为双曲线C 的左、右焦点.（1）若点P 在双曲线的右支上，且12F PF ∆的面积为3，求点P 的坐标；（2）若斜率为1且经过右焦点2F 的直线l 与双曲线交于,M N 两点，求线段MN 的长度. 13．设抛物线24C y x =：，F 为C 的焦点，过F 的直线l 与C 交于A B ，两点. （1）设l 的斜率为2，求AB 的值； （2）求证：OA OB ⋅为定值.14．已知椭圆M ：22213x y a +=()0a >的一个焦点为()1,0F -，左右顶点分别为A ，B ．经过点F 的直线l与椭圆M 交于C ，D 两点． （Ⅰ）求椭圆M 方程；（Ⅰ）当直线l 的倾斜角为45时，求线段CD 的长；（Ⅰ）记ⅠABD 与ⅠABC 的面积分别为1S 和2S ，求12S S -的最大值．15．已知椭圆C ：()222210x y a b a b +=>>的离心率为12，点31,2A ⎛⎫ ⎪⎝⎭在椭圆C 上，直线1l 过椭圆C 的右焦点与上顶点，动直线2l ：y kx =与椭圆C 交于M ，N 两点，交1l 于P 点. （1）求椭圆C 的方程；（2）已知O 为坐标原点，若点P 满足14OP MN =，求此时MN 的长度.16．已知椭圆()22:10E a b a b+=>>，O 为坐标原点，P 为椭圆上任意一点，1F ，2F 分别为椭圆的左、右焦点，且2b a =，过点()0,1M 的动直线l 与椭圆相交于A ，B 两点. (1)求椭圆E的标准方程；(2)当AB =l 的方程 17．如图，椭圆2222:1x y C a b+=（0a b >>）的离心率为12，过椭圆右焦点F 作两条互相垂直的弦AB 与CD ．当直线AB 的斜率为0时，AB 4=．（Ⅰ）求椭圆的方程；（Ⅰ）求使AB CD +取最小值时直线AB 的方程．18．已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为2，且过点F 的直线l 被抛物线C 所截得的弦长MN 为8． （1）求直线l 的方程；（2）当直线l 的斜率大于零时，求过点,M N 且与抛物线C 的准线相切的圆的方程．19．椭圆C ：(222212x y m m m+=>，直线l 过点()1,1P ，交椭圆于A ､B 两点，且P 为AB 的中点. （1）求直线l 的方程；（2）若AB =，求m 的值.20．如图所示，已知圆()221:116F x y ++=上有一动点Q ，点2F 的坐标为()1,0，四边形12QF F R 为平行四边形，线段1F R 的垂直平分线交2F R 于点P ，设点P 的轨迹为曲线C .（1）求曲线C 的方程；（2）过点2F 的直线l 与曲线C 有两个不同的交点A 、B ，问是否存在实数λ，使得2222AF BF AF BF λ+=⋅成立，若存在求出λ的值；若不存在，请说明理由.21．已知椭圆22:14x W y +=，直线l 过点(0,2)-与椭圆W 交于两点,A B ，O 为坐标原点.（1）设C 为AB 的中点，当直线l 的斜率为32时，求线段OC 的长； （2）当ⅠOAB 面积等于1时，求直线l 的斜率.22．已知抛物线24W y x =：的焦点为F ，直线2+y x t =与抛物线W 相交于,A B 两点. （1）将||AB 表示为t 的函数；（2）若||AB =AFB △的周长.23．如图，过点(1,0)F 的直线l 与抛物线2:4C y x =交于,A B 两点.（1）若||8AB =，求直线l 的方程;（2）记抛物线C 的准线为l '，设直线,OA OB 分别交l '于点,N M ，求ON OM ⋅的值.24．设椭圆E ：22221x y a b+=（a ，b >0）过M （2 ，N 1)两点，O 为坐标原点，（1）求椭圆E 的方程；（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E 恒有两个交点A ，B ，且OA OB ⊥？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由.25．折纸又称“工艺折纸”，是一种把纸张折成各种不同形状物品的艺术活动，在我国源远流长. 某些折纸活动蕴含丰富的数学内容，例如：用圆形纸片，按如下步骤折纸（如下图），步骤1：设圆心是O ，在圆内不是圆心处取一点，标记为F ； 步骤2：把纸片对折，使圆周正好通过F ； 步骤3：把纸片展开，于是就留下一条折痕；步骤4：不停重复步骤2和3，能得到越来越多条的折痕．所有这些折痕围成的图形是一个椭圆.若取半径为4的圆形纸片，设定点F 到圆心O 的距离为2，按上述方法折纸.（1）建立适当的坐标系，求折痕围成椭圆的标准方程； （2）求经过F ，且与直线FO 夹角为4π的直线被椭圆截得的弦长.四、填空题26．在平面直角坐标系xOy 中，过抛物线2:C y mx =的焦点F 作斜率为1的直线，与抛物线C 交于A ，B 两点．若弦AB 的长为6，则实数m 的值为__________.27．已知抛物线C : y 2=2px (p >0)，直线l ：y = 2x + b 经过抛物线C 的焦点，且与C 相交于A 、B 两点．若|AB | = 5，则p = ___．28．已知抛物线2:4,C x y =AB 为过焦点F 的弦，过,A B 分别作抛物线的切线，两切线交于点P ，设112200(,),(,),(,)A x y B x y P x y ，则下列结论正确的有________．Ⅰ若直线AB 的斜率为-1，则弦8AB =； Ⅰ若直线AB 的斜率为-1，则02x =； Ⅰ点P 恒在平行于x 轴的直线1y =-上； Ⅰ若点(,)M M M x y 是弦AB 的中点，则0M x x =．五、双空题29．已知抛物线()2:20C x py p =>的焦点为F ，直线():0l y kx b k =+≠与抛物线C 交于A ，B 两点，且6AF BF +=，线段AB 的垂直平分线过点()0,4M ，则抛物线C 的方程是______；若直线l 过点F ，则k =______.专题01 圆锥曲线中的弦长问题一、单选题1．设椭圆长半轴长为a ，短半轴长为b ，半焦距为c ，则过焦点且垂直于长轴的弦长是（ ）A ．2b aB ．22c aC ．2c aD ．22b a【答案】D 【分析】设椭圆焦点在x 轴上，椭圆的标准方程为()222210x y a b a b+=>>，将x c =或x c =-代入椭圆的标准方程，求出y ，由此可求得结果. 【详解】设椭圆焦点在x 轴上，椭圆的标准方程为()222210x y a b a b+=>>，将x c =或x c =-代入椭圆的标准方程得22221c y a b +=，2222222221y c a c b b a a a -∴=-==， 解得2b y a =±，因此，过焦点且垂直于长轴的弦长是22b a. 故选：D.2．已知椭圆22:12x C y +=，直线l 过椭圆C 的左焦点F 且交椭圆于A ，B 两点，AB 的中垂线交x 轴于M点，则2||||FM AB 的取值范围为（ ）A ．11,164⎛⎫⎪⎝⎭ B ．11,84⎡⎫⎪⎢⎣⎭C ．11,162⎛⎫⎪⎝⎭ D ．11,82⎡⎫⎪⎢⎣⎭【答案】B 【分析】 当l ：0y =时，2||1||8FM AB =，设():10l x my m =-≠与椭圆联立可得：()222210m y my +--=， 然后求得AB 的中垂线方程，令0y = ，得21,02M m ⎛⎫-⎪+⎝⎭，然后分别利用两点间的距离公式和弦长公式求得||MF ，2||AB ，建立2||||FM AB 求解.【详解】椭圆22:12x C y +=的左焦点为()1,0F -,当l ：0y =时，())(),,0,0A BM ，1,FM AB ==所以2||1||8FM AB =，设():10l x my m =-≠与椭圆联立22112x my x y =-⎧⎪⎨+=⎪⎩，可得： ()222210my my +--=，由韦达定理得：1221222212m y y m y y m ⎧+=⎪⎪+⎨-⎪=⎪+⎩，取AB 中点为222,22m D m m -⎛⎫⎪++⎝⎭， 所以AB 的中垂线方程为：2212:22DM m l x y m m m ⎛⎫=--- ⎪++⎝⎭， 令0y = ，得21,02M m ⎛⎫-⎪+⎝⎭， 所以221||2m MF m +=+，又()()2222281||2m AB m +==+， 所以2222||121111=1(,)||818184FM m AB m m ⎛⎫+⎛⎫=+∈ ⎪ ⎪++⎝⎭⎝⎭， 综上所述2||11,||84FM AB ⎡⎫∈⎪⎢⎣⎭， 故选：B. 【点睛】思路点睛：1、解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单．2、设直线与椭圆的交点坐标为A (x 1，y 1)，B (x 2，y 2)，则弦长为AB ===(k 为直线斜率)． 注意：利用公式计算直线被椭圆截得的弦长是在方程有解的情况下进行的，不要忽略判别式大于零． 3．过椭圆9x 2+25y 2=225的右焦点且倾斜角为45°的弦长AB 的长为（ ） A ．5 B ．6C ．9017D ．7【答案】C 【分析】求出焦点坐标和直线方程，与椭圆方程联立，利用韦达定理和弦长公式可得答案. 【详解】由9x 2+25y 2=225得，221259x y +=，2225,9a b ==，所以216c =，右焦点坐标为(4,0)，直线AB 的方程为4y x =-，所以2241259y x x y =-⎧⎪⎨+=⎪⎩得2342001750x x -+=，设1122(,),(,)A x y B x y ，所以1212100175,1734x x x x +==，||AB ==9017==. 故选：C. 【点睛】本题主要考查直线与椭圆的弦长公式||AB =.4．椭圆()2222:10x y C a b a b+=>>的左、右焦点分别是1F 、2F ，斜率为12的直线l 过左焦点1F 且交C 于A ，B 两点，且2ABF 的内切圆的周长是2π，若椭圆C 的离心率为13,24e ⎡⎤∈⎢⎥⎣⎦，则线段AB 的长度的取值范围是（ ）A ．⎣B ．⎣C ．⎣⎦D ．⎣⎦【答案】B 【分析】先利用等面积法可得：12114222a r c y y ⨯⋅=⨯⋅-，求解出12y y -的值，然后根据弦长公式12AB y =-的取值范围. 【详解】设内切圆半径为r ，由题意得12114222a r c y y ⨯⋅=⨯⋅-得1228,43y y e ⎡⎤-=∈⎢⎥⎣⎦，1212AB y y y =-=-∈⎣. 故选：B. 【点睛】本题考查椭圆焦点三角形问题，考查弦长的取值范围问题，难度一般.解答时，等面积法、弦长公式的运用是关键.二、多选题5．已知抛物线()220y px p =>的焦点为F ，过点F 的直线l 交抛物线于A 、B 两点，以线段AB 为直径的圆交y 轴于M 、N 两点，则（ ）A ．若抛物线上存在一点()2,E t 到焦点F 的距离等于3，则抛物线的方程为24y x =B ．若2AF BF =，则直线l 的斜率为C ．若直线l 43p AB =D ．设线段AB 的中点为P ，若点F 到抛物线准线的距离为2，则sin PMN ∠的最小值为12【答案】AD 【分析】由抛物线的定义求得p 的值，可判断A 选项的正误；设直线l 的方程为2px my =+，设点()11,A x y 、()22,B x y ，将直线l 的方程与抛物线的方程联立，结合韦达定理可求得m 的值，可判断B 选项的正误；利用韦达定理结合抛物线的焦点弦长公式可判断C 选项的正误；设直线l 的方程为1x my =+，设点()11,A x y 、()22,B x y ，联立直线l 与抛物线的方程，求得点P 到y 轴的距离和AB ，可得出sin PMN ∠关于m 的表达式，可判断D 选项的正误. 【详解】对于A 选项，由抛物线的定义可得232pEF =+=，解得2p =， 所以，抛物线的标准方程为24y x =，A 选项正确； 对于B 选项，如下图所示： 抛物线的焦点为,02p F ⎛⎫⎪⎝⎭，设点()11,A x y 、()22,B x y ，设直线AB 的方程为2p x my =+，联立222p x my y px⎧=+⎪⎨⎪=⎩，消去x 并整理得2220y mpy p --=，222440m p p ∆=+>恒成立，由韦达定理可得122y y mp +=，212y y p =-，由于2AF BF =，由图象可得2AF FB =，即1122,2,22p p x y x y ⎛⎫⎛⎫--=- ⎪ ⎪⎝⎭⎝⎭， 所以，122y y =-，可得121221222y y y y mp y y p =-⎧⎪+=⎨⎪=-⎩，解得4m =±，所以，直线l的斜率为1m=±B 选项错误； 对于C 选项，当直线lB选项可知，3m =，12y y p +=，由抛物线的焦点弦长公式可得)12128223AB x x p y y p p p p =++=++=+=，C 选项错误；对于D 选项，抛物线的焦点F 到准线的距离为2p =，则该抛物线的方程为24y x =. 设直线l 的方程为1x my =+，设点()11,A x y 、()22,B x y ，联立214x my y x=+⎧⎨=⎩，消去x 可得2440y my --=，216160m ∆=+>， 则124y y m +=，()21212242x x m y y m ∴+=++=+，()212241AB x x m =++=+，点P 到y 轴的距离为212212x x d m +==+， 所以，()22221111sin 1112222212dm PMN m m AB+∠===-≥-=++， 当且仅当0m =时，等号成立，D 选项正确.故选：AD. 【点睛】本题考查直线与抛物线的综合问题，考查了抛物线焦点弦的几何性质以及焦点弦长、焦半径的计算.本题中将直线方程与抛物线的方程联立，利用韦达定理得出点A 、B 的纵坐标所满足的关系，并结合了抛物线的焦点弦长公式进行计算，考查学生的运算求解能力，属于中等题. 三、解答题6．如图，P 是直线:3l y x =+上一动点，过点P 且与l 垂直的直线l '交抛物线2:C y x =于A ，B 两点，点A 在P ，B 之间．（1）若l '过抛物线C 的焦点F ，求AB ；（2）求PA PB的最小值．【答案】（1）2；（2．【分析】（1）先求出直线l '的方程，联立直线与抛物线，将韦达定理和弦长公式相结合即可得结果； （2）设:AB y x t =-+，联立方程组分别求出A ，B ，P 的纵坐标，将PA PB表示为关于t 的函数式，结合基本不等式即可得结果. 【详解】解：（1）由已知得1,04F ⎛⎫⎪⎝⎭，所以1:4l y x '=-+，联立得214y x y x⎧=-+⎪⎨⎪=⎩，消去x ，可得2104y y +-=，设点()11,A x y ，()22,B x y ，由根与系数的关系得121114y y y y +=-⎧⎪⎨=-⎪⎩，所以AB=122y y -==．（2）设:AB y x t =-+，由2y x ty x=-+⎧⎨=⎩，消去x ，可知20y yt +-=，∵有两个不同的交点，∴11404t t ∆=+>⇒>-，解得：A y =，B y =，由3y x t y x =-+⎧⎨=+⎩，得32P t y +=，由于点A 在点P ，点B 之间，所以1P A P B PA y y PBy y -===-，()0u u =>，所以288111151544PAu PBu u u u=-=-≥=++++当且仅当u =72t =时取等号． 故PA PB的最小值为1911-．【点睛】 关键点点睛：（1）直线弦长公式的应用；（2）将所求量表示为关于t 的函数，利用基本不等式求最值.7．已知椭圆22221x y a b+=（0a b >>）长轴长为短轴长的两倍，连结椭圆的四个顶点得到的菱形的面积为4，直线l 过点(,0)A a -，且与椭圆相交于另一点B ． （1）求椭圆的方程； （2）若线段ABl 的倾斜角． 【答案】（1）2214x y +=；（2）4π或34π． 【分析】（1）由题设列出基本量方程组，解得基本量，从而得方程.（2）设直线l 方程，代入椭圆方程得关于x 的一元二次方程，韦达定理整体思想及弦长公式得关于斜率的方程，解得斜率得直线方程. 【详解】(1)由题意可知22222212242b a a b a b c ⨯=⎧⎪⎪⨯⨯⨯=⎨⎪=+⎪⎩， 2a = ，1b =，c =。

在 Rt△MNF 中， | MF | = 于是 | NF | 3 = ， cosα 4 － cos2 α
为定值， 并说明理由． 分析 本题第（ 2 ） 小题 是一个 典 型 的 解 析 几 何 定 图5 值问题， 通常可运用函数的 思想方法解之， 其解题过程可归纳为： 一选， 二求， 三定值． 具体操作程序如下： 一选： 选择参变量． 需要证明为定值的量在通 常情况下应该是变量， 它应该随某一个量的变化而 可选择这个量为参变量． 变化， 二求： 求出函数的解析式． 即把需要证明为定 值的量表示成关于上述参变量的函数 ． 三定值： 化简函数解析式得到定值． 由题目的 结论可知要证明为定值的量必与参变量的大小无 故求出的函数必为常数函数， 因此， 只需对上述 关， 函数的解析式进行必要的化简即可得到定值 ． 1］ 文献［ 介绍的解法 1 （ 复杂解法 ） 选择以直 线 AB 的斜率 k 为目标函数的变量； 解法 2 （ 简捷解 法） 选择线段 AB 的中点 N 的横坐标为目标函数的 变量． 在运用函数的思想方法解决定值问题时， 目 标函数变量的选择显得很重要． 由于角度形式的焦 半径公式与本题相关的线段可直接对话 ， 因此也可 AB x 选择直线 与 轴的夹角 α 为目标函数的变量． 解 π α ＜ ． 不妨设 | AF | ＞ | BF | ， 则由椭圆的焦半径公 2 式可知 b2 3 | AF | = = ； a － ccosα 2 － cosα b2 3 | BF | = = ， a + ccosα 2 + cosα 2 3 + = 从而 | AB | = | AF | + | FB | = 2 － cosα 2 + cosα 12 ． 4 － cos2 α 设 AB 的中点为 N， 则 2 3 2 | FN | = | AF | － | FB | = － = 2 － cosα 2 + cosα 6cosα ， 4 － cos2 α 3cosα | FN | = ． 即 4 － cos2 α （ 2 ） 设直线 AB 与 x 轴的夹角为 α， 则0 ＜

圆锥曲线有关焦点弦的几个公式及应用如果圆锥曲线的一条弦所在的直线经过焦点，则称此弦为焦点弦。

圆锥曲线的焦点弦问题涉及到离心率、直线斜率（或倾斜角）、定比分点（向量）、焦半径和焦点弦长等有关知识。

焦点弦是圆锥曲线的“动脉神经”，集数学知识、思想方法和解题策略于一体，倍受命题人青睐，在近几年的高考中频频亮相，题型多为小题且位置靠后属客观题中的压轴题，也有作为大题进行考查的。

本文介绍圆锥曲线有关焦点弦问题的几个重要公式及应用，与大家交流。

定理1已知点是离心率为的圆锥曲线的焦点，过点的弦与的焦点所在的轴的夹角为，且。

（1）当焦点内分弦时，有；（2）当焦点外分弦时（此时曲线为双曲线），有。

证明设直线是焦点所对应的准线，点在直线上的射影分别为，点在直线上的射影为。

由圆锥曲线的统一定义得，，又，所以。

（1）当焦点内分弦时。

如图1，，所以。

图1（2）当焦点外分弦时（此时曲线为双曲线）。

如图2，，所以。

图2评注特别要注意焦点外分焦点弦（此时曲线为双曲线）和内分焦点弦时公式的不同，这一点很容易不加区别而出错。

例1（2009年高考全国卷Ⅱ理科题）已知双曲线的右焦点为，过且斜率为的直线交于两点。

若，则的离心率为（）解这里，所以，又，代入公式得，所以，故选。

例2（2010年高考全国卷Ⅱ理科第12题）已知椭圆的离心率为。

过右焦点且斜率为的直线于相交于两点，若，则（）解这里，，设直线的倾斜角为，代入公式得，所以，所以，故选。

例3 （08高考江西卷理科第15题）过抛物线的焦点作倾斜角为的直线，与抛物线交于两点（点在轴左侧），则有＿＿＿＿图3解如图3，由题意知直线与抛物线的地称轴的夹角，当点在轴左侧时，设，又，代入公式得，解得，所以。

例4（2010年高考全国卷Ⅰ理科第16题）已知是椭圆的一个焦点，是短轴的一个端点，线段的延长线交于点，且，则的离心率为＿＿＿解设直线与焦点所在的轴的夹角为，则，又，代入公式得，所以。

例5（自编题）已知双曲线的离心率为，过左焦点且斜率为的直线交的两支于两点。

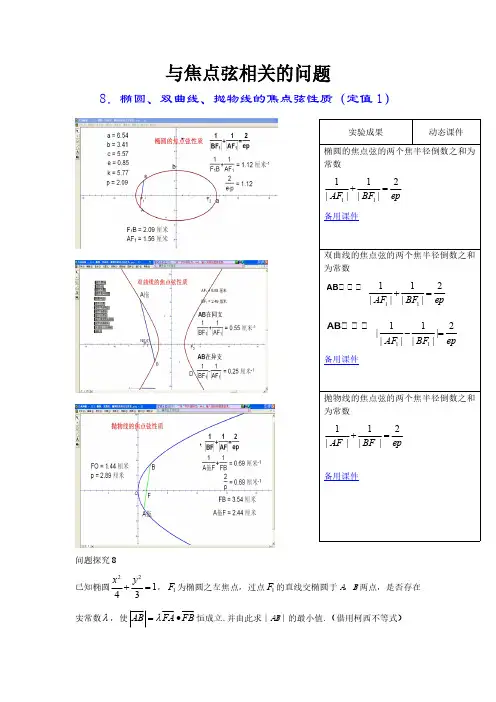
与焦点弦相关的问题8．椭圆、双曲线、抛物线的焦点弦性质（定值1）问题探究8已知椭圆22143x y +=，1F 为椭圆之左焦点，过点1F 的直线交椭圆于A ，B 两点，是否存在实常数λ，使AB FA FB λ=•u u u r u u u r u u u r恒成立.并由此求∣AB ∣的最小值.（借用柯西不等式）9．椭圆、双曲线、抛物线的正交焦点弦性质（定值2）问题探究9已知椭圆22143x y +=，1F 为椭圆之左焦点，过点1F 的直线12,l l 分别交椭圆于A ，B 两点和C ，D 两点，且12l l ⊥，是否存在实常数λ，使AB CD AB CD λ+=•u u u r u u u r u u u r u u u r恒成立.并由此求四边形ABCD 面积的最小值和最大值.实验成果动态课件椭圆互相垂直的焦点弦倒数之和为常数epe CD AB 22||1||12-=+ 备用课件双曲线互相垂直的焦点弦倒数之和为常数epe CD AB 2|2|||1||12-=+ 备用课件抛物线互相垂直的焦点弦倒数之和为常数epe CD AB 22||1||12-=+ 备用课件10．椭圆、双曲线、抛物线的焦点弦与其中垂线性质（定值3）问题探究10已知椭圆22143x y+=，1F为椭圆之左焦点，过点1F的直线交椭实验成果动态课件设椭圆焦点弦AB的中垂线交长轴于点D，则∣DF∣与∣AB∣之比为离心率的一半（F为焦点）备用课件设双曲线焦点弦AB的中垂线交焦点所在直线于点D，则∣DF∣与∣AB∣之比为离心率的一半（F为焦点）备用课件设抛物线焦点弦AB的中垂线与对称轴交于点D，则∣DF∣与∣AB∣之比为离心率的一半（F为焦点）备用课件圆于A ，B 两点，AB 中垂线交x 轴于点D ，是否存在实常数λ，使1AB F D λ=u u u r u u u u r恒成立？11．椭圆、双曲线、抛物线的焦点弦性质1（中点共线）问题探究11已知椭圆22143x y +=，1F 为椭圆之左焦点，过点1F 的直线1l 交实验成果动态课件椭圆的焦点弦的端点在相应准线上的投影与端点的交叉连线与对称轴的交点平分焦点与准线与对称轴的交点线段． 备用课件双曲线的焦点弦的端点在相应准线上投影与端点的交叉连线与对称轴的交点平分焦点与准线与对称轴的交点线段． 备用课件抛物线的焦点弦的端点在相应准线上投影与端点的交叉连线与对称轴的交点平分焦点与准线与对称轴的交点线段． 备用课件椭圆于A ，B 两点，直线2l ：4x =-交x 轴于点G ，点,A B 在直线2l 上的射影分别是,N M ，设直线,AM BN 的交点为D ，是否存在实常数λ，使1GD DF λ=u u u r u u u u r恒成立.12．椭圆、双曲线、抛物线的焦点弦性质2（三点共线）问题探究12已知椭圆22143x y +=，1F 为椭圆之左焦点，过点1F 的直线1l 交椭圆于A ，B 两点， ,C D 分别为椭圆的左、右顶点，动点P 满足,,PA AD PC CB λμ==u u u r u u u r u u u r u u u r试探究点P 的轨迹.抛物线焦点弦端点A 、B 与另一顶点D 连线与相应准线的交点N 、M ，则N 、C 、B 三点共线，M 、C 、A 三点共线（抛物线的D 点在无穷远处）.备用课件13．椭圆、双曲线、抛物线的焦点弦性质3（对焦点直张角）问题探究13已知双曲线22131x y -=，1F 为双曲线之左焦点，过点1F 的直线1l 交双曲线于A ，B 两点， ,C D 分别为双曲线的左、右顶点，动点P 满足11,,PA AD PC CB λμ==u u u r u u u r u u u r u u u r动点Q 满足22,,QA AC QB BD λμ==u u u r u u u r u u u r u u u r试探究1PF Q ∠是否为定值.14．椭圆、双曲线、抛物线的相交焦点弦与准线关系问题探究14已知椭圆22143x y +=，1F 为椭圆之左焦点，过点1F 的直线12,l l 分别交椭圆于A ，B 两点和C ，D 两点，直线2l ：4x =-，直线AD 交直线2l 于点P ，试判断点P 、C 、B 是否三点共线，并证明之.抛物线的任意两焦点弦端点所在直线交点的轨迹是准线 备用课件15．椭圆、双曲线、抛物线的相交焦点弦与准线关系（角平分线）问题探究15已知椭圆22143x y +=，1F 为椭圆之左焦点，过点1F 的直线12,l l 分别交椭圆于A ，B 两点和C ，D 两点，直线3l ：4x =-，直线AD 交直线3l 于点P ，试证明11PF A PF D ∠=∠.抛物线的任意两焦点弦端点所在直线交点必在准线上且交点和焦点的连线平分AF D ∠ 备用课件16．椭圆、双曲线、抛物线的相交弦与准线关系推广问题探究16已知椭圆22184x y +=，过点(2,0)N 的直线12,l l 分别交椭圆于A ，B 两点和C ，D 两点，设直线AD 与直线CB 交于点P ，试证明点P 的轨迹为直线4x =.实验成果动态课件过椭圆长轴上任意一点N （0,t ）的两条弦端点的直线的交点的轨迹是一定直线ta x 2=备用课件过双曲线实轴上任意一点N （0,t ）的两条弦端点的直线的交点的轨迹是一定直线ta x 2=备用课件过抛物线对称轴上任意一定点N （0,t ）的两条弦端点的直线的交点的轨迹是一定直线t x -= 备用课件17．椭圆、双曲线、抛物线的焦点弦直线被曲线及对称轴所分比之和为定值问题探究17已知椭圆22184x y +=，点1F 为椭圆之左焦点，过点1F 的直线1l 分别交椭圆于A ，B 两点，设直线AB 与y 轴于点M ，11,,MA AF MB BF λμ==u u u r u u u r u u u r u u u r试求λμ+的值.过抛物线的焦点弦所在直线被曲线及顶点处的切线所分比之和为定值. 备用课件18．椭圆、双曲线、抛物线的焦半径向量模的比之和为定值问题探究18已知方向向量为3)e =r 的直线l 过点(0,3)A -和椭圆2222:1x y C a b+=(0)a b >>的焦点，且椭圆C 的中心O 和椭圆的右准线上的点B 满足：0,OB e AB AO •==u u u r r u u u r u u u r.⑴求椭圆C的方程；⑵设E 为椭圆C 上任一点，过焦点12,F F 的弦分别为,ES ET ,设111,EF FS λ=u u u r u u u r 222EF F T λ=u u u u r u u u r，求12λλ+的值.实验成果动态课件过椭圆上任点A 作两焦点的焦点弦AC ，AB ，其共线向量比之和为定值．即1112222122121AF m F B AF m F B e m m e →→→→==++==-定值备用课件过双曲线上任点A 作两焦点的焦点弦AC ，AB ，其共线向量比之和为定值．即1112222122121AF m F B AF m F B e m m e→→→→==++==-定值备用课件（注：图中测算不是向量，故中间一式用的是差）由于抛物线的开放性，焦点只有一个，故准线相应地替换了焦点，即PA=m 1AF PB=m 2BF备用课件m 1+m 2=0。

圆锥曲线中的弦长问题一、单选题1．椭圆2214x y +=的两个焦点为1F 、2F ，过1F 作垂直于x 轴的直线与椭圆相交，一个交点为P ，则2PF =（ ）A ．2B C ．72D ．42．直线l 过抛物线22y x =的焦点F ，且l 与该抛物线交于不同的两点()11,A x y ，()22,B x y ．若12 3x x +=，则弦AB 的长是（ ）A ．4B ．5C ．6D ．83．焦点为F 的抛物线2:4C y x =的对称轴与准线交于点E ，点P 在抛物线C 上，在EFP △中，sin EFP FEP ∠=∠，则||EP 的值是（ ）A ．B ．4C ．2D ．14．椭圆()2222:10x y C a b a b+=>>的左、右焦点分别是1F 、2F ，斜率为12的直线l过左焦点1F 且交C 于A ，B 两点，且2ABF 的内切圆的周长是2π，若椭圆C 的离心率为13,24e ⎡⎤∈⎢⎥⎣⎦，则线段AB 的长度的取值范围是（ ）A ．,3⎡⎢⎣B ．3⎡⎢⎣C ．,48⎣⎦D ．816⎣⎦5．已知抛物线2:4C y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与抛物线C 的一个交点，若4PF FQ =，则QF =（ ） A ．3 B ．52C ．32D ．32或52二、填空题6．已知P 为椭圆221164x y +=上的一个动点，过点P 作圆()2211x y -+=的两条切线，切点分别是A ，B ，则AB 的最小值为_______.7．已知抛物线C ：22x py =-()0p >的焦点F 与22184y x +=的一个焦点重合，过焦点F 的直线与C 交于A ，B 两不同点，抛物线C 在A ，B 两点处的切线相交于点M ，且M 的横坐标为2，则弦长AB =______.8．已知1F ，2F 为椭圆221123x y+=的两个焦点，点P 在椭圆上，如果线段1PF 的中点在y 轴上，则1PF 的值为______.三、解答题9．如图，在平面直角坐标系xOy 中，已知椭圆1C ：22221x y a b +=和椭圆2C ：22221x y c b+=，其中0a c b >>>，222a b c =+，1C ，2C 的离心率分别为1e ，2e ，且满足12:2:3e e =，A ，B 分别是椭圆2C 的右、下顶点，直线AB 与椭圆1C 的另一个交点为P ，且185PB =.（1）求椭圆1C 的方程；（2）与椭圆2C 相切的直线MN 交椭圆1C 与点M ，N ，求MN 的最大值.10．在平面直角坐标系上，已知动点P 到定点()11,0F -、()21,0F 的距离之和为2. （1）求动点P 的轨迹方程C ．（2）若直线:l y x t =+与曲线C 交于A 、B 两点，423AB =.求t 的值11．已知椭圆222:1(1)x E y a a +=>的离心率为32，右顶点为(,0)P a ，P 是抛物线2:2(0)C y px p =>的焦点．（1）求抛物线C 的标准方程；（2）若C 上存在两动点,A B （,A B 在x 轴两侧）满足20OA OB ⋅=（O 为坐标原点），且PAB △的周长为2||4AB +，求||AB ．12．已知椭圆2222:1(0)x y G a b a b +=>>的离心率为1,2过椭圆G 右焦点2(1,0)F 的直线m ：x =1与椭圆G 交于点M (点M 在第一象限) （1）求椭圆G 的方程；（2）连接点M 与左焦点并延长交椭圆于点N ，求线段MN 的长.13．已知抛物线21:2C y px =的焦点与椭圆222:198x y C +=的右焦点F 重合，过抛物线1C 的准线l 上一点P 作抛物线1C 的两条切线，切点为A ，B .（1）求证：直线AB 过焦点F ； （2）若8PA =，6PB =，求PF 的值.14．已知椭圆2222:1x y E a b+=()0a b >>的半焦距为c ，原点O 到经过两点()(),0,0,c b 的直线的距离为12c ，椭圆的长轴长为43.（1）求椭圆E 的方程；（2）直线l 与椭圆交于,A B 两点，线段AB 的中点为()2,1M -，求弦长.AB 15．已知直线l 经过抛物线26y x =的焦点F ，且与抛物线交于A 、B 两点. （1）若直线l 的倾斜角为60，求线段AB 的长； （2）若2AF =，求BF 的长.16．已知圆上224x y +=上任取一点P ，过点P 作y 轴的垂线段PQ ，垂足为Q ，当P在圆上运动时，线段PQ 中点为M . （1）求点M 的轨迹方程；（2）若直线l 的方程为y ＝x －1，与点M 的轨迹交于A ，B 两点，求弦AB 的长.一、单选题1．椭圆2214x y +=的两个焦点为1F 、2F ，过1F 作垂直于x 轴的直线与椭圆相交，一个交点为P ，则2PF =（ ） A ．3 B ．3C ．72D ．4【答案】C 【解析】 试题分析：，所以当时，，而,所以,故选C.考点：椭圆的性质2．直线l 过抛物线22y x =的焦点F ，且l 与该抛物线交于不同的两点()11,A x y ，()22,B x y ．若12 3x x +=，则弦AB 的长是（ ）A ．4B ．5C ．6D ．8【答案】A 【分析】由题意得1p =，再结合抛物线的定义即可求解. 【详解】 由题意得1p =，由抛物线的定义知：121231422p pAB AF BF x x x x p =+=+++=++=+=， 故选：A 【点睛】本题主要考查了抛物线的几何性质，考查抛物线的定义，属于基础题.3．焦点为F 的抛物线2:4C y x =的对称轴与准线交于点E ，点P 在抛物线C 上，在EFP △中，sin 2EFP FEP ∠=∠，则||EP 的值是（ ）A ．2B ．4C ．2D ．1【答案】A 【分析】过点P 作PH 垂直于准线于点H ，由双曲线的定义得cos PF PH m FEP ==∠，在EFP △中利用正弦定理可求出FEP ∠，带入所给等式即可推出2EFP π∠=，即可求得PE 的值. 【详解】如图所示，过点P 作PH 垂直于准线于点H ，设PE m =，则cos PF PH m FEP ==∠， 在EFP △中，由正弦定理知sin sin PF PEPEF EFP=∠∠，即cos sin 2sin m FEP FEP FEP∠=∠∠，所以2cos 2FEP ∠=，又()0,FEP π∠∈，所以4FEP π∠=，则sin 21EFP FEP ∠=∠=，又()0,EFP π∠∈，所以2EFP π∠=，在直角EFP △中，2EF =，4FEP π∠=，所以22PE =故选：A 【点睛】本题考查抛物线的定义与几何性质、正弦定理解三角形，属于中档题.4．椭圆()2222:10x y C a b a b+=>>的左、右焦点分别是1F 、2F ，斜率为12的直线l过左焦点1F 且交C 于A ，B 两点，且2ABF 的内切圆的周长是2π，若椭圆C 的离心率为13,24e ⎡⎤∈⎢⎥⎣⎦，则线段AB 的长度的取值范围是（ ）A ．45,253⎡⎢⎣B ．85453⎡⎢⎣C ．535,48⎣⎦D ．535816⎣⎦【答案】B【分析】先利用等面积法可得：12114222a r c y y ⨯⋅=⨯⋅-，求解出12y y -的值，然后根据弦长公式12AB y =-的取值范围. 【详解】设内切圆半径为r ，由题意得12114222a r c y y ⨯⋅=⨯⋅-得1228,43y y e ⎡⎤-=∈⎢⎥⎣⎦，1212AB y y y =-=-∈⎣. 故选：B. 【点睛】本题考查椭圆焦点三角形问题，考查弦长的取值范围问题，难度一般.解答时，等面积法、弦长公式的运用是关键.5．已知抛物线2:4C y x =的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与抛物线C 的一个交点，若4PF FQ =，则QF =（ ） A ．3 B ．52C ．32D ．32或52【答案】B 【分析】设点()1,P t -，利用4PF FQ =求得点Q 的横坐标，利用抛物线的定义可求得QF . 【详解】抛物线C 的焦点为()1,0F ，准线l 的方程为1x =-.设点()1,P t -、(),Q x y ，则()2,PF t =-，()1,FQ x y =-，4PF FQ =，可得()412x -=，解得32x =， 由抛物线的定义可得35122QF =+=. 故选：B. 【点睛】本题考查利用抛物线的定义求焦半径，求出点Q 的坐标是解题的关键，考查计算能力，属于中等题.二、填空题6．已知P为椭圆221 164xy+=上的一个动点，过点P作圆()2211x y-+=的两条切线，切点分别是A，B，则AB的最小值为_______..【答案】422.【分析】连接PC，交AB于H，可得H为AB中点，求得圆心和半径，连接AC，BC，可得,AC PA BC PB⊥⊥，运用勾股定理和三角形面积公式可得AB，设()4cos,2sinPθθ，[]0,2θπ∈，运用两点的距离公式和同角的平方关系，结合配方和二次函数的最值求法，可得所求最小值.【详解】如图，连接PC，交AB于H，可得H为AB中点，圆()2211x y-+=的圆心为()1,0C，半径1r=，连接AC，BC，可得,AC PA BC PB⊥⊥，则21PA PB PC==-又222121221PCPA ACAB AHPC PC PC-⋅====-设()4cos,2sinPθθ，[]0,2θπ∈，可得()()2 2222111 4cos12sin12cos8cos512cos33PCθθθθθ⎛⎫=-+=-+=-+⎪⎝⎭，当1cos 3θ=时，2PC 取得最小值为113，此时AB 取得最小值为11=.故答案为：11. 【点睛】本题考查椭圆中的最值问题，涉及圆的相切问题，属于中档题7．已知抛物线C ：22x py =-()0p >的焦点F 与22184y x +=的一个焦点重合，过焦点F 的直线与C 交于A ，B 两不同点，抛物线C 在A ，B 两点处的切线相交于点M ，且M 的横坐标为2，则弦长AB =______. 【答案】10 【分析】首先根据已知条件得到抛物线方程为28xy ，设直线AB 方程为2y kx =-，()11,A x y ，()22,B x y ，利用导数的几何意义得到两条切线分别为21148x x y x =-+和22248x x y x =-+，联立切线得到122M x x x +=，从而得到124x x +=，联立直线AB 与抛物线，利用韦达定理即可得到12k =-，再求焦点弦长即可. 【详解】由题意可得()0,2F -，则4p =，抛物线方程为28xy .设直线AB 方程为2y kx =-，()11,A x y ，()22,B x y ，其中2118x y =-，2228x y =-. 由28x y =-得4x y '=-，所以在点A 处的切线方程为()1114x y y x x -=--，化简得21148x x y x =-+①，同理可得在点B 处的切线方程为22248x x y x =-+②.联立①②得122M x x x +=，又M 的横坐标为2， 124x x ∴+=.将AB 方程代入抛物线得28160x kx +-=，1284x x k ∴+=-=，12k ∴=-，()1212144462y y k x x ∴+=+-=-⨯-=-，1210AB p y y ∴=--=.故答案为：10 【点睛】本题主要考查抛物线的焦点弦，同时考查导数的几何意义，属于中档题.8．已知1F ，2F 为椭圆221123x y+=的两个焦点，点P 在椭圆上，如果线段1PF 的中点在y 轴上，则1PF 的值为______.【分析】由题意可得PF 2平行y 轴，然后结合椭圆方程和椭圆的定义整理计算即可求得最终结果. 【详解】∵原点O 是F 1F 2的中点，∴PF 2平行y 轴，即PF 2垂直于x 轴， ∵c =3，∴|F 1F 2|=6，设|PF 1|=x，根据椭圆定义可知2PF x =，∴22)36x x +=，解得2x =.. 【点睛】本题主要考查椭圆的几何性质，方程的思想等知识，意在考查学生的转化能力和计算求解能力.三、解答题9．如图，在平面直角坐标系xOy 中，已知椭圆1C ：22221x y a b +=和椭圆2C ：22221x y c b+=，其中0a c b >>>，222a b c =+，1C ，2C 的离心率分别为1e ，2e ，且满足12:2:3e e =，A ，B 分别是椭圆2C 的右、下顶点，直线AB 与椭圆1C 的另一个交点为P ，且185PB =.（1）求椭圆1C 的方程；（2）与椭圆2C 相切的直线MN 交椭圆1C 与点M ，N ，求MN 的最大值.【答案】（1）22193x y +=；（232. 【分析】（1）由12:3e e =可得得42243840c a c a -+=，化为2232a c =，从而3a b ，2c b =， )2,0Ab ，()0,B b -，则直线AB 的方程为2y x b =-，与椭圆方程联立，利用弦长公式求得3b =（2）当直线MN 的斜率不存在时，易得2MN =，当直线MN 的斜率存在时，设直线MN ：()0y kx m k =+≠，与椭圆2C ：22163x y +=联立并消去y ，利用韦达定理、弦长公式表示出弦长，结合配方法可得答案. 【详解】（1）由题意知1c e a =，222222c b c ae --==， 因为12:3e e =22232c c a a c-=⋅，222223a c a c -=，将等号两边同时平方，得42243840c a c a -+=，即()()22222230a cac --=，所以2232a c =，又222a b c =+，所以3a b，c =，所以),0A，()0,B b -，所以直线AB的方程为y x b =-， 与椭圆1C ：222213x y b b +=联立并消去y，得222332x x b b ⎛⎫+-= ⎪ ⎪⎝⎭， 整理得10x =，25x =，所以,55b P ⎛⎫ ⎪ ⎪⎝⎭， 因为185PB =185=，得b =3a =，椭圆1C 的方程为22193x y +=.（2）当直线MN 的斜率不存在时，易得2MN =.当直线MN 的斜率存在时，设直线MN ：()0y kx m k =+≠，与椭圆2C ：22163x y +=联立并消去y ， 得()222124260kxknx m +++-=，因为直线MN 与椭圆2C 相切，所以()()222216412260k m k m∆=-+-=，整理得()22630*k m +-=，将直线MN 与椭圆1C 方程联立并消去y ，得()222136390k x kmx m +++-=，由()*式可得()()()22222223641339129336k m kmk m k ∆=-+-=+-=.设(),M M M x y ，(),N N N x y ，则2613M N km x x k -+=+，223913M N m x x k-=+，所以M N MN x =-==设213k t +=，则1t >，2MN ==22<，所以当4t =，即1k =±时，MN 最大，且最大值为322. 【点睛】求椭圆标准方程的方法一般为待定系数法,根据条件确定关于,,a b c 的方程组，解出,,a b ，从而写出椭圆的标准方程．解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决，往往会更简单.10．在平面直角坐标系上，已知动点P 到定点()11,0F -、()21,0F 的距离之和为22. （1）求动点P 的轨迹方程C ．（2）若直线:l y x t =+与曲线C 交于A 、B 两点，423AB =.求t 的值 【答案】（1）2212x y +=；（2）1t =±.【分析】（1）求出,a b 可求椭圆的方程.（2）设点()11,A x y ，()22,B x y ，联立直线方程和椭圆方程，消去y 后利用韦达定理和弦长公式公式可得关于t 的方程，解方程后可得t 的值.【详解】解：（1）因为1222PF PF +=P 轨迹为椭圆，并且长轴长222a =， 因为焦点坐标分别为()1,0-，()1,0，所以22c =，又因为222a b c =+，所以1b =，所以P 点运动轨迹椭圆C 的方程为2212x y +=.（2）设点()11,A x y ，()22,B x y ，因为22220x y y x t⎧+-=⎨=+⎩，消元化简得2234220x tx t ++-=，所以()2221612222480t t t ∆=--=->，1221243223t x x t x x ⎧+=-⎪⎪⎨-⎪=⎪⎩，所以3AB ==又因为3AB =3=， 解得1t =±，满足>0∆，所以1t =±. 【点睛】直线与圆锥曲线的位置关系，一般可通过联立方程组并消元得到关于x 或y 的一元二次方程，再把要求解的目标代数式化为关于两个的交点横坐标或纵坐标的关系式，该关系中含有1212,x x x x +或1212,y y y y +，最后利用韦达定理把关系式转化为某一个变量的方程，解此方程即可.11．已知椭圆222:1(1)x E y a a +=>的离心率为2，右顶点为(,0)P a ，P 是抛物线2:2(0)C y px p =>的焦点．（1）求抛物线C 的标准方程；（2）若C 上存在两动点,A B （,A B 在x 轴两侧）满足20OA OB ⋅=（O 为坐标原点），且PAB △的周长为2||4AB +，求||AB ． 【答案】（1）28y x =；（2）30. 【分析】(1)根据椭圆离心率的关系可得2a =，进而根据抛物线的性质求出方程即可. (2) 设直线:AB x my n =+，联立28y x =得出韦达定理，再结合抛物线的方程与20OA OB ⋅=化简可得10n =，再根据抛物线的焦半径公式以及弦长公式求得2m =±，进而求得||AB . 【详解】解析：（1）因为椭圆222:1x E y a +=22134a a -=， 解得24a =，所以2a =， 而22p=，所以4p =， 从而得抛物线C 的标准方程为28y x =.（2）由题意0AB k ≠，设直线:AB x my n =+， 联立28y x =得2880y my n --=， 设()()1122,,,A x y B x y （其中120y y <） 所以12128,8y y m y y n +=⋅=-，且0n >，因为20OA OB ⋅=，所以22121212122064y y OA OB x x y y y y ⋅=+=+=，2820n n -=，所以(10)(2)0n n -+=，故10n =或2n =-（舍）， 直线:10AB x my =+， 因为PAB △的周长为2||4AB + 所以||||||2||4PA PB AB AB ++=+. 即||||||4PA PB AB +=+，因为()21212||||424824PA PB x x m y y m +=++=++=+.又12||AB y y =-=所以2820m +=解得2m =±，所以||30AB ==.【点睛】本题主要考查了联立直线与抛物线的方程，结合韦达定理与弦长公式、焦半径公式求解的问题，属于中档题.12．已知椭圆2222:1(0)x y G a b a b +=>>的离心率为1,2过椭圆G 右焦点2(1,0)F 的直线m ：x =1与椭圆G 交于点M (点M 在第一象限) （1）求椭圆G 的方程；（2）连接点M 与左焦点并延长交椭圆于点N ，求线段MN 的长.【答案】（1）22143x y +=（2）257【分析】（1）由已知条件推导出1c =，12c a =，由此能求出椭圆的方程． （2）依题意可得直线1MF 的方程，联立直线与椭圆方程，消元，求出两交点的横坐标，再根据弦长公式计算可得； 【详解】 解：（1）椭圆2222:1(0)x y G a b a b+=>>的离心率为12，过椭圆G 右焦点2(1,0)F 的直线:1m x =与椭圆G 交于点M （点M 在第一象限），1c ∴=，12c a =，解得2a =， 2223b a c ∴=-=，∴椭圆的方程为22143x y +=．（2）依题意可得()11,0F -，31,2M ⎛⎫⎪⎝⎭，所以1MF ：3344y x =+ 联立方程得223344143y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩，消去y 整理得22118390x x +-=，则()()121390x x -+=解得11x =，2137x =-所以121325177MN x ⎤⎛⎫=-=--= ⎪⎥⎝⎭⎦【点睛】本题考查待定系数法求椭圆方程，直线与椭圆的综合应用，弦长公式的应用，属于中档题.13．已知抛物线21:2C y px =的焦点与椭圆222:198x y C +=的右焦点F 重合，过抛物线1C 的准线l 上一点P 作抛物线1C 的两条切线，切点为A ，B .（1）求证：直线AB 过焦点F ； （2）若8PA =，6PB =，求PF 的值. 【答案】（1）证明见解析；（2）245. 【分析】（1）求出椭圆的右集合，即抛物线的焦点，从而可得p 值，得抛物线方程，设点()11,A x y ，()22,B x y ，()1,P a -，由切点设出切线方程11:()PA y y k x x -=-，由相切求出斜率k ，得切线PA 方程，同理得PB 方程，代入P 点坐标后可得过,A B 两点的直线方程，得证其过焦点；（2）由（1）中直线AB 方程与抛物线方程联立后消元应用韦达定理，然后可证得PA PB ⊥，又可证得PF AB ⊥，这样由直角三角形性质可得PF【详解】（1）证明：因为椭圆222:198x y C +=的右焦点()1,0F ，所以12p=，即2p =.所以抛物线1C 的方程为24y x =. 设点()11,A x y ，()22,B x y ，()1,P a -，设()111:PA y y k x x -=-， 联立()1112,4,y y k x x y x ⎧-=-⎨=⎩消x 得211114440yy y x k k -+-=， 由0∆=得2111110k y k x -+=.又2114y x =，故2211111104k y k y -+=，故2111102k y ⎛⎫-= ⎪⎝⎭，故112PA k k y ==，故直线PA 的方程为()1112y y x x y -=-， 即1122yy x x =+.同理22PB k y =，直线PB 的方程为2222yy x x =+. 又点P 在直线PA ，PB 上，所以112222,22,ay x ay x =-+⎧⎨=-+⎩故()11,A x y ，()22,B x y 在直线22ay x =-+上，故直线AB 的方程为22ay x =-+，令0y =，得1x =，所以直线AB 过焦点F .（2）解：由（1）知联立222,4,ay x y x =-+⎧⎨=⎩消x 得2240y ay --=，故122y y a +=，124y y =-，故12221PA PB k k y y ⋅=⋅=-， 故直线PA 与直线PB垂直，从而10AB ==.因为2AB k a =，0112PF a ak -==---，所以1PF AB k k ⋅=-， 故PF AB ⊥，所以6824105PF ⨯==. 【点睛】本题主要考查直线与抛物线的位置关系，解题方法是设而不求的思想方法，本题中设出两切点坐标1122(,),(,)A x y B x y ，由直线AB 方程与抛物线方程联立方程组消元后应用韦达定理，然后代入PA PB k k ⋅可得垂直．这是直线与圆锥曲线相交问题常用的方法．14．已知椭圆2222:1x y E a b +=()0a b >>的半焦距为c ，原点O 到经过两点()(),0,0,c b 的直线的距离为12c，椭圆的长轴长为 （1）求椭圆E 的方程；（2）直线l 与椭圆交于,A B 两点，线段AB 的中点为()2,1M -，求弦长.AB【答案】（1）221123x y +=；（2）10. 【分析】（1）由点到直线的距离得12b a =，再由长轴长可求得,a b 得椭圆方程；（2）直线AB 的斜率一定存在，设方程为()12y k x +=-，代入椭圆方程整理，设()()1122,,,A x y B x y ，由韦达定理得1212,x x x x +，由中点坐标公式求得k ，再由弦长公式求得弦长． 【详解】解：（1）经过两点()(),0,0,c b 的直线为：1x yc b+=即0bx cy bc +-=.由已知：原点到直线的距离12bc d c a ===即12b a =因为2a =b =所以椭圆的标准方程为：221123x y +=（2）当直线l 斜率不存在时，线段AB 的中点在x 轴上，不合题意.所以直线l 的斜率存在，设为k ，则直线()12y k x +=-即为：21y kx k =-- 设()()1122,,,A x y B x y 联立22214120y kx k x y =--⎧⎨+-=⎩得：()()22214821161680k x k k x k k +++++-= ()()22214821161680k xk k x k k +-+++-=显然>0∆ 则()122821414k k x x k++==+，解得12k = 则212216168214k k x x k +-⋅==+所以12AB x =-==【点睛】本题考查求椭圆的标准方程，考查求直线与椭圆相交弦长，解题方法是设而不求的思想方法，即设交点坐标1122(,),(,)x y x y ，设直线方程，代入椭圆方程应用韦达定理，得1212,x x x x +，由弦长公式得弦长．15．已知直线l 经过抛物线26y x =的焦点F ，且与抛物线交于A 、B 两点.（1）若直线l 的倾斜角为60，求线段AB 的长； （2）若2AF =，求BF 的长. 【答案】（1）8；（2）6. 【分析】（1）设点()11,A x y 、()22,B x y ，求出直线l 的方程，与抛物线方程联立，求出12x x +的值，再利用抛物线的焦点弦长公式可求得线段AB 的长； （2）设直线l 的方程为32x my =+，设点()11,A x y 、()22,B x y ，将直线l 的方程与抛物线的方程联立，可得出129y y =-，由2AF =求得1x 的值，利用韦达定理以及抛物线的方程求得2x 的值，利用抛物线的定义可求得BF 的长. 【详解】（1）设点()11,A x y 、()22,B x y ，抛物线26y x =的焦点为3,02F ⎛⎫⎪⎝⎭， 由于直线l 过点F ，且该直线的倾斜角为60，则直线l的方程为32y x ⎫=-⎪⎭，联立2326y x y x⎧⎫=-⎪⎪⎭⎨⎪=⎩，消去y 并整理得29504x x -+=，259160∆=-=>， 由韦达定理可得125x x +=，由抛物线的焦点弦长公式可得123538AB x x =++=+=；（2）设点()11,A x y 、()22,B x y ，由题意可知，直线l 不可能与x 轴重合，设直线l 的方程为32x my =+， 联立2326x my y x⎧=+⎪⎨⎪=⎩，消去x 并整理得2690y my --=，()23610m ∆=+>，由韦达定理可得126y y m +=，129y y =-，1322AF x =+=，可得112x =，21163y x ∴==，129y y ∴=-，则22218127y y ==，222962y x ∴==，因此，2362BF x =+=.【点睛】有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式12AB x x p =++，若不过焦点，则必须用一般弦长公式．16．已知圆上224x y +=上任取一点P ，过点P 作y 轴的垂线段PQ ，垂足为Q ，当P在圆上运动时，线段PQ 中点为M .（1）求点M 的轨迹方程；（2）若直线l 的方程为y ＝x －1，与点M 的轨迹交于A ，B 两点，求弦AB 的长.【答案】（1）2214y x +=；（2【分析】（1）设M 、P ，利用相关点法即可求解.（2）将直线与椭圆方程联立，利用弦长公式即可求解.【详解】（1）设(),M x y ，()00,P x y ，()00,Q y ∴，点M 是线段PQ 中点，002,x x y y ∴==，又()00,P x y 在圆224x y +=上，()2224x y +=， 即点M 的轨迹方程为2214y x +=. （2）联立22114y x y x =-⎧⎪⎨+=⎪⎩，消去y 可得，25230x x --=， ()22600∆=-+>，设()11,A x y ，()22,B x y ， 则1225x x +=，1235x x =，12AB x ∴=-===. 【点睛】方法点睛：本题考查了轨迹问题、求弦长，求轨迹的常用方法如下：（1）定义法：利用圆锥曲线的定义求解. （2）相关点法：由已知点的轨迹进行求解. （3）直接法：根据题意，列出方程即可求解.。

问题探究8已知椭圆，为椭圆之左焦点，过点22143x y +=1F 1F 实常数，使恒成立.并由此求∣AB λAB FA FB λ=∙问题探究9已知椭圆，为椭圆之左焦点，过点的直线22143x y +=1F 1F C ，D 两点，且，是否存在实常数，使12l l ⊥λAB + 四边形ABCD 面积的最小值和最大值.问题探究10已知椭圆，为椭圆之左焦点，过点22143x y +=1F F 线交轴于点D ，是否存在实常数，使x λAB F λ=问题探究11已知椭圆，为椭圆之左焦点，过点的直线22143x y +=1F 1F 交轴于点G ，点在直线上的射影分别是4x =-x ,A B 2l N D ，是否存在实常数，使恒成立.λ1GD DF λ=问题探究12已知椭圆，为椭圆之左焦点，过点的直线22143x y +=1F 1F 别为椭圆的左、右顶点，动点满足P ,PA AD PC λμ== 椭圆焦点弦端点连线与相应准线的交点N 、共线备用课件双曲线焦点弦端点点则三点共线备用课件抛物线焦点弦端点点则三点共线处）备用课件问题探究13已知双曲线，为双曲线之左焦点，过点的直线22131x y -=1F 1F 分别为双曲线的左、右顶点，动点满足,C D P 1PA AD λ= 试探究是否为定值.22,,QA AC QB BD λμ==1PF Q ∠椭圆焦点弦端点连线与相应准线的交点1NF ⊥备用课件双曲线焦点弦端点点D 连线与相应准线的交点则NF备用课件抛物线焦点弦端点点D 连线与相应准线的交点则NF 无穷远处）备用课件问题探究14已知椭圆，为椭圆之左焦点，过点的直线22143x y +=1F 1F C ，D 两点，直线：，直线AD 交直线于点2l 4x =-2l 并证明之.问题探究15已知椭圆，为椭圆之左焦点，过点的直线22143x y +=1F 1F 1,l l C ，D 两点，直线：，直线AD 交直线于点P ，试证明3l 4x =-3l问题探究16已知椭圆，过点的直线分别交椭圆于22184x y +=(2,0)N 12,l l 线AD 与直线CB 交于点P ，试证明点P 的轨迹为直线问题探究17已知椭圆，点为椭圆之左焦点，过点的直线22184x y +=1F 1F 设直线AB 与轴于点，试求y M 11,,MA AF MB BF λμ==问题探究18 已知方向向量为的直线过点和椭圆(1,3)e = l (0,23)A -焦点，且椭圆的中心和椭圆的右准线上的点满足：C O B 圆的方程；⑵设为椭圆上任一点，过焦点的弦分别为C E C 12,F F ，求的值. 222EF F T λ= 12λλ+。

圆锥曲线有关焦点弦的几个公式及应用如果圆锥曲线的一条弦所在的直线经过焦点，则称此弦为焦点弦。

圆锥曲线的焦点弦问题涉及到离心率、直线斜率（或倾斜角）、定比分点（向量）、焦半径和焦点弦长等有关知识。

焦点弦是圆锥曲线的“动脉神经”，集数学知识、思想方法和解题策略于一体，倍受命题人青睐，在近几年的高考中频频亮相，题型多为小题且位置靠后属客观题中的压轴题，也有作为大题进行考查的。

本文介绍圆锥曲线有关焦点弦问题的几个重要公式及应用，与大家交流。

定理1已知点是离心率为的圆锥曲线的焦点，过点的弦与的焦点所在的轴的夹角为，且。

（1）当焦点内分弦时，有；（2）当焦点外分弦时（此时曲线为双曲线），有。

证明设直线是焦点所对应的准线，点在直线上的射影分别为，点在直线上的射影为。

由圆锥曲线的统一定义得，，又，所以。

（1）当焦点内分弦时。

如图1，，所以。

图1（2）当焦点外分弦时（此时曲线为双曲线）。

如图2，，所以。

图2评注特别要注意焦点外分焦点弦（此时曲线为双曲线）和内分焦点弦时公式的不同，这一点很容易不加区别而出错。

例1（2009年高考全国卷Ⅱ理科题）已知双曲线的右焦点为，过且斜率为的直线交于两点。

若，则的离心率为（）解这里，所以，又，代入公式得，所以，故选。

例2（2010年高考全国卷Ⅱ理科第12题）已知椭圆的离心率为。

过右焦点且斜率为的直线于相交于两点，若，则（）解这里，，设直线的倾斜角为，代入公式得，所以，所以，故选。

例3 （08高考江西卷理科第15题）过抛物线的焦点作倾斜角为的直线，与抛物线交于两点（点在轴左侧），则有＿＿＿＿图3解如图3，由题意知直线与抛物线的地称轴的夹角，当点在轴左侧时，设，又，代入公式得，解得，所以。

例4（2010年高考全国卷Ⅰ理科第16题）已知是椭圆的一个焦点，是短轴的一个端点，线段的延长线交于点，且，则的离心率为＿＿＿解设直线与焦点所在的轴的夹角为，则，又，代入公式得，所以。

例5（自编题）已知双曲线的离心率为，过左焦点且斜率为的直线交的两支于两点。

用圆锥曲线焦点弦结论巧算高考题重庆巴蜀科学城中学校（401331）李兰［摘要］圆锥曲线焦点弦结论具有统一形式，利用焦点弦结论可以快速解决高考题，为考生打开解题思路，提高学生的解题能力。

［关键词］圆锥曲线；焦点弦；高考题［中图分类号］G633.6［文献标识码］A［文章编号］1674-6058（2023）17-0024-03一、公式及其证明圆锥曲线中的焦点弦就是过焦点的弦长，弦长公式AB=1+k2||x1-x2，圆锥曲线有统一方程，思考由抛物线的焦点弦与弦长倾斜角度、离心率（抛物线的离心率为1）有关的弦长公式，类比推导圆锥曲线的另一个统一公式：焦半径=半通径1±e⋅cosθ=b2a1±e⋅cosθ（半通径就是垂直于焦点所在轴的焦半径，抛物线为y2=2px(p>0)中的p）。

证明如下：①椭圆x2a2+y2b2=1中，直线l过右焦点F与椭圆交于A、B两点，其中A（x1，y1），B（x2，y2），l的倾斜角为θ（锐角），则焦半径AF=b2a1+e·cosθ，BF=b2a1-e·cosθ。

（如图1）x=a2cθ图1由A、B两点分别向右准线作垂线，垂足为M、N，由A点向x轴作垂线，垂足为D，由圆锥曲线统一定义，椭圆上点到焦点的距离比到准线的距离等于离心率得||AF||AM=ca，所以||AF=||AM e=e·()a2c-x1=a-ex1，||FD=||AF cosθ。

所以c+||AF cosθ=x1，即c+||AF cosθ=a-||AFe，即||AF（1+e cosθ）=a-c2a=b2a。

所以AF=b2a1+e·cosθ，同理BF=b2a1-e·cosθ。

②双曲线x2a2-y2b2=1中，直线l过焦点F与同一支交于A、B两点，结论同上，证明略。

③抛物线y2=2px（p>0），直线l过右焦点F与抛物线交于A、B两点，则AF=p1-cosθ，BF=p1+cosθ，长短视角度而定。

文档圆锥曲线焦点弦长的一个公式在高考中的妙用圆锥曲线的焦点弦问题是高考命题的大热点，主要是在解答题中，全国文科一般为压轴题的第题，几乎每一年都有考察。

由于题目的综合性很高的，21题或者第2022题，理科和各省市一般为第运算量很大，属于高难度题目，考试的得分率极低。

本文介绍的焦点弦长公式是圆锥曲线（椭圆、双曲线和抛物线）的通用公式，它是解决这类问题的金钥匙，利用这个公式使得极其复杂的问题变得简?单明了，中等学习程度的学生完全能够得心应手！，焦点为(或平行于坐标轴)定理已知圆锥曲线（椭圆、双曲线或者抛物线）的对称轴为坐标轴?l，通径长两点，记圆锥曲线的离心率为eF，且与圆锥曲线交于A、F，设倾斜角为的直线B经过 H，则为H?||AB的长；（1）当焦点在x轴上时，弦AB22?|cos|1?eH?||AB.的长（2）当焦点在y轴上时，弦AB22?|sin?e|1.轴上，中心在原点的双曲线为例证明，其它情形请读者自证x本文仅对焦点在222b2yxca b?H1???e 所AB＞0）证明：设双曲线方程为，通径，弦（，离心率＞0，22aaba??l?tanlk）c（x?ky?为直线，其参数方程为在的直线，的方程为的倾斜角）（其中?，tcosx??c??为参数）（t. ??.tsiny??4222222???0??t）?t??（a2sinbb?bcosccos. 代入双曲线方程并整理得： t的几何意义可得：由|AB|?|t?t|212?（t?t）?4tt212122?bcos4?2bc2?（?）?22222222????cosab?bsinsincos?a2ab2?2222??|?|asinbcos2b2?22?|cosa|1?e2b2a?22?|?ecos|1H.?22?|e1|?cos文档推论H|AB|?在椭圆、抛物线或双曲线的一支上时，轴上，当A、B（1）焦点在；当x22?cose1?HH?|?|AB||AB. A、B不在双曲线的一支上时，；当圆锥曲线是抛物线时，222??sin?1ecosH?||AB；当B在椭圆、抛物线或双曲线的一支上时，（2）焦点在y轴上，当A、22?sin?e1HH?|?|ABAB||. ；当圆锥曲线是抛物线时，A、B不在双曲线的一支上时，222??cosesin?1典题妙解下面以近年高考题为例说明上述结论在解题中的妙用.22yx2C?C：?1px2?（y?m）p、，已知椭圆且抛物线例1（06（湖南文第＞0）21题），1143CC 的右焦点过椭圆.的公共弦AB12AB?xC的焦点是否在直线AB上；（Ⅰ）当m的值，并判断抛物线轴时，求p，24C p?（Ⅱ）若AB的方程. 且抛物线上，求的焦点在直线ABm的值及直线231x?AB?x0??m.关于轴时，点A、Bx轴对称，的方程为，直线（Ⅰ）当解：AB33），（1）?（1，. 的坐标为或从而点A22C 上，在抛物线A点299p?..?2p?即849C（0），的焦点坐标为此时抛物线上，该焦点不在直线AB. 216????.的倾斜角为，由（Ⅰ）知（Ⅱ）设直线AB2?）?tan1（?x?y. 则直线AB的方程为8Ce?1x?p?2Hmy? ，于是有，离心率平行于AB的对称轴轴，焦点在上，通径抛物线238H.?AB|?|22??）31?cossin（2b21C H3???e 的右焦点，通径AB又，离心率过椭圆. 1a2文档y 12H.??|AB|?A222??cos4cos?|1?e|128F.??222??cos?）4（31?cos Ox12??6??，tancos?.解之得：B72?C）mF（，）1x?y?tan（? 的焦点上，在直线抛物线2361???mtan??m?.，从而336?m0??y?66x；时，直线当AB的方程为36?m?0?y?66x?. 当时，直线AB的方程为322yx FFF1??题）已知椭圆22（07，过全国Ⅰ文第的直线例的左、右焦点分别为2、12123BDAC?F P.的直线交椭圆于A、C两点，且交椭圆于B、D两点，过，垂足为222yx00）y（x，?1.，证明：＜）设（1P点的坐标为0023.（2）求四边形ABCD的面积的最小值22yx1??b2，ca?3，1??）证明：在1. （中，23FF，90?PF ?F?是的中点，O2121122.?1x?y.OP?||??1F|F|?c得00212221?y?x?.在圆P上点22yx221??1?x?y在椭圆. 显然，圆的内部2322yx00?1.故＜23???BDAC??.（2AC的倾斜角，由的倾斜角为）解：如图，设直线BD可知，直线2文档23342b?e??H.，离心率通径33a FF 、又、BDAC分别过椭圆的左、右焦点，于是2134H?BD，||?y222??cos?e3cos1?A34H.?|AC|?D ?2?sin?322?）cos（1?e?P2F O F x? ABCD的面积四边形B211C?||BD|?AC|S233414???22??2sin?cos3?396.???2???][0，，?sin21 ??0，.2?224?sin96??4?S?，.??25??96. 面积的最小值为ABCD故四边形25l、题文第22题）双曲线的中心为原点O，焦点在x上，两条渐近线分别为（例308全国Ⅰ理第211llll|||ABOB||OA|成等. 、B两点、已知，经过右焦点F垂直于的直线分别交、、于A2121FABF.同向差数列，且与（Ⅰ）求双曲线的离心率；.，求双曲线的方程（Ⅱ）设AB被双曲线所截得的线段的长为422yxa b1??.解：）＞（＞0，0（Ⅰ）设双曲线的方程为22ba d??OA|OA||AB|||OB||md?|m|?m?|OBAB| ，、，公差为d，成等差数列，设、，则22222222)dm?m(?d)?m?(ddm?m2?dm?d?m?m2??. . 即mm35m?d?OB||?OA||?. 从而. ，444文档b??ll2AOB??x?y. ，则. 又设直线的方程为的倾斜角为11a4AB||b????tan2AOB?tan?..tan??而3||OAa b?2?42tan a y???.b2?3tan1?ll2)(1?12a A 1b M.?解之得：2a xF O5b2N .?(?1?)e?2a B??????., 则F的直线AB的倾斜角为（Ⅱ）设过焦点212)(2?1tan22???sin??cos.?sin???. 而12?5tan1?2)?(1212??cos?.52bb2?bH?2b??通径. aaH4?|MN|? .N. 于是有：又设直线AB与双曲线的交点为M、22?cose1?b4?.即152?1?()526?ab?3.解得，从而22yx1???所求的椭圆方程为. 936金指点睛2y2l1??x|AB|过椭圆的直线=_________. B的上焦点F交椭圆于A、两点，则1. 已知斜率为142?y2l?1x?线则2. 过曲双，两、于曲线的为斜作点左的焦F倾角直交双线AB点36||AB=_________.文档22l0x?2y?2?的最大面AOBA、B两点，O3. 已知椭圆作直线，过左焦点F为坐标原点，求△交. 积yBF xO A2S2px4y?m|AB|?p，弦AB过焦点F，设，△4. 已知抛物线AOB的面积为S（，求证：＞0）m y. 为定值Ax F OB2y2?x?1四点都在椭圆N、M、题）为椭圆在上，Fy轴正半轴上的焦5.（05全国Ⅱ文第22P、Q2MFPFFQ FN0?MFPF?的面积的最大值和PQMN共线，共线，且点. 已知与.与求四边形. 最小值yMQFPxO N2?x?8y、A的焦点如图，倾斜角为题重庆文第6. (0722)的直线经过抛物线F，且与抛物线交于. 两点B文档l F的坐标及准线的方程；（Ⅰ）求抛物线的焦点??x2|cos||FP|?FP为定值，P交，证明（Ⅱ）若轴于点为锐角，作线段AB的垂直平分线m. 并求此定值yDC AE?xF O P m Bl)2F(0,0?l:y?31.的距离比它到直线的距离小7. 点M与点 M（1）求点的轨迹方程；.、B；C、D. 求四边形ACBD的最小面积（2）经过点F且互相垂直的两条直线与轨迹相交于A2x22FF1?y?x?y2?与椭圆的焦点相同，且以抛物线、的准线为8. 已知双曲线的左右焦点215.其中一条准线 1（）求双曲线的方程；F的面积的ACBDD. ；C、（2）若经过焦点求四边形且互相垂直的两条直线与双曲线相交于A、B2. 最小值参考答案2?b23c?l?1?H?e?3a??2,b?1,c?，通径 .，离心率1. ，直线解：的倾斜角a2a481H???|AB|? .22?5sin1?e2322)(()?1?222?b2c??H?6?2?e?23,c??a1,b?，通径. 2. ，直线的倾斜角，离心率解：a6a6H3AB|???|? .22?|?1ecos|322|)?|1?2(22x2c21?y??e?1?1,c??a2,b)0?F(1,径通解3. 焦，左点：率离，，心，22a文档2b22H??.a2b2x?ll?H|?2AB|?1??c||OF轴，这时的斜率不存在时，的当直线，△，高AOB a21?1?S?2?. 面积22??ll)?(x?1y?tan即为当直线存的斜率在时，设直线，的倾斜角为其，则方程???||0?tan|?0?tantan|?sind?????0tan??x?ytan?.O，原点到直线AB的距离?||sec2?1?tan222H22???|AB|?.2222???sin?coscos2?11?e222?cos)?(?12?sin21?d|?|AB??S?. 的面积△AOB y2?2sin1?B?? ＜0＜，F ?2??sin sin?sin?21?.＞0. 从而xO A?22sin?S??.?22sin?2??1sin??. AOB的最大面积为，即”号成立当且仅当. 故△时，“=22)0F(p,p4H?，通径4. 解：焦点为.xAB?p|OF|??|AB|?m4p的面积，△轴，这时，高当直线AB的斜率不存在时，AOB12p?2??|AB|?|OF|S.2424p4pS43p????.，是定值p4mm??)px?ytan??(即为，方倾设存AB当直线的斜率在时，直线的斜角为，则其程??|tanpp|tan||?sin?d??p??0??ant?xyp?tan.ABO，原点到直线的距离?||sec2?1?tan文档p4H??|AB|. 22??sinsin2p21?dS??|AB|??.的面积△AOB y?sin2A2244?sin44pp1S3p??????. 22??pm4msinsin x O F B2S33p?p?在什么位置，均有（不论直线. 为定值）AB m2y2.1c?1，?a?2，b?x?1解：在椭圆5. 中，2）1（0，F PQMN?. 是椭圆的两条弦，相交于焦点，且由已知条件，MN和PQ????.如图，设直线PQ的倾斜角为的倾斜角，则直线MN22b22y??2H?e .，离心率通径于是有Ma2QF2H2P，|?MN|??2?cos?222?)(esin?1?xO 2N2H2.?|?|PQ222??sin2sin?1?e?的面积四边形PQMN1?S|PQ||MN|?222212???22??2sin2?cos?216.???2???]1[0，?sin2， ??0，.2?28?sin16??2S?，?.??9??162. PQMN故四边形面积的最小值和最大值分别为和9),20(4p?,?2p8?，的坐标为6.（Ⅰ）解：抛物线的焦点，F文档lx??2.准线的方程为FD?AClAC?H?2p?8. 于C（Ⅱ）证明：作，D. 通径于H8y??cos|AFcos|,|ADAB|?|??,|EF|?|FP||. 则 D22??sinsin CA?4|cos??AD|p?|AF|AF|?|AC|?|?.E? xO F P 4m ?AF||?.B?cos1??cos4414l??|?|?AF|?|AE||AF|?AB?|EF||?，22???cos21?sinsin|EF|4??||FP. 从而2??cossin42???)2?(1?|cos2cos?|FP?2sin||?8FP|?|FP?. 2?sin?2|cos|?|FP|FP为定值，此定值为故8.F(0,2)l:y??2的距离相等，的距离与它到直线7. 解：（1）根据题意，点M与点F(0,2)l:y??2?是它的准线点是它的焦点，直线.M的轨迹是抛物线，点p?2p?4?. 从而，22?8xy?.所求的点M的轨迹方程是 两条互相垂直的直线与抛物线均有两个交点， 2）（y??的倾斜角为，它们的斜率都存在. 如图，设直线AB DB??90?. 的倾斜角为则直线CD82H?p?，于是有：抛物线的通径FA CH8H8xO ?,||?CD|??|AB.2222????sin?)cos(90?coscos?四边形ACBD的面积1|AB|?|CD|S?2881???22??2sincos128.?2?2sin2???128S?2sin?45??90?,2.，这时当且仅当时，取得最大值1min?四边形ACBD的最小面积为128.文档2x222)(?2,0FF(2,0)1y??2?a??ba?5,b?1,c?，、8. . 解：其焦点为（1中，在椭圆）1251p2x2??y??x1p??. 在抛物线中，其准线方程为，2221a22c?2,?3a?1,b?c??a?在双曲线中，. ，c22y2?1x??所求的双曲线的方程为. 3 两条互相垂直的直线与双曲线均有两个交点，）（2???90??.CD. 如图，设直线AB的倾斜角为的倾斜角为，则直线它们的斜率都存在2b2c?6H?2e??双曲线的通径. 于是有：，离心率aaH6H6?,|CD|??|AB|?.222222????sin4?11?e)cos?1e?cos(41?cos90??四边形ACBD的面积yl A11|CD??|AB||S2C661???xO 22??2sin41?14cos?F B 218.? D 2?2sin4?3?l22???18?S2sin?45?,?2?90.时，1当且仅当，这时取得最大值min?四边形ACBD的最小面积为18.。

圆锥曲线专题03焦点弦问题焦点弦是经过椭圆，双曲线或者抛物线焦点的弦，这里我们以椭圆为例，如下图。

组成焦点弦的因素有3个：线段MN 的长度，直线MN 的倾斜角以及点F 分线段MN 的比例关系，所以在研究焦点弦问题当中我们重点从以上三个因素进行考虑。

一、焦点弦长的求法法一：利用弦长公式|AB |==若要使用弦长公式，我们需要设出AB 所在直线的方程，然后联立椭圆，利用韦达定理求出,A B 两点之间横坐标或纵坐标的和与积的关系即可，这也是我们在圆锥曲线中求弦长最常用的方法。

法二：利用直线的参数方程在参数方程中我们也学过求弦长的方法，此法和弦长公式差不多，但是在解决选做题参数方程的题目中经常用到，该发在参数方程专题中将重点讲解。

设A 点参数为1t ，B 点参数为2t ，则12|AB |||t t =-方法三：焦点弦长公式已知圆锥曲线C 的离心率为e，焦点为F，焦准距（焦点到准线的距离）为p，过点F 的弦MN 与曲线C的焦点所在的轴的夹角为,(0,90]θθ︒∈，则有222|MN ||1e cos |ep θ=-，在抛物线内22|MN |sin pθ=证明过程如下：设11(x ,y )N ，根据第二定义可知211'()a NF eNN e x a ex c==-=-在RT DNF ∆中，1cos x OD OF DF c NF θ==-=-，代入上式得：(cos )NF a e c NF θ=--，解得cos 1ec aNF e θ-=-同理可得2222222||cos 1cos ab ep MF a c e θθ==--例1：已知椭圆22221x y a b+=的右焦点为F，经过F 且倾斜角为60︒的直线与椭圆相交于不同的两点A,B ，已知2AF FB = .（1）求离心率；（2）若15|AB |=4，求椭圆方程.【解析】（1）求离心率套公式即可1cos 1e λθλ-=+，代入求得23e =套用公式22215|AB |||1cos 4ep e θ==-解得252a p c c =-=又因为23e =，故可解出3,a b ==，椭圆方程为22195x y +=例2：已知F 为抛物线2:4C y x =的焦点，过F 作两条互相垂直的直线12,l l ，直线1l 与C 交于,A B 两点，直线2l 与C 交于,D E 两点，则|AB ||DE |+的最小值为________.例3：过抛物线2:4C y x =的焦点的直线交C 于点M（M 在x 轴上方），l 为C的准线，点N 在l 上且MN l ⊥，则M 到直线NF 的距离为_________.二、在焦点弦中,,e θλ三要素之间的关系上面求得焦点弦长公式与离心率e 有关，因此下面我们探究一下求离心率，倾斜角以及点分线段的比例之间的关系。

圆锥曲线中焦点弦的取值范围的探究本文主要探究圆锥曲线中焦点弦的取值范围，尤其时焦点弦弦长何时取最小值和最大值，运用直线的参数方程和弦长公式，得出椭圆、抛物线、双曲线的焦点弦的取值范围的以下结论：结论1：椭圆焦点弦AB 的取值范围为⎥⎦⎤⎢⎣⎡a a b 2,22，其中最小值为椭圆的通经长，最大值为椭圆的长轴长；结论2：抛物线焦点弦AB 的取值范围为[)+∞,2p ，其中最小值为抛物线的通经长；结论3：（1）若b a ≥时，双曲线的焦点弦AB 的取值范围为⎪⎭⎫⎢⎣⎡+∞,22a b ，其中最小值为双曲线的通经长； （2）若b a <时，双曲线的焦点弦AB 的取值范围为[)+∞,2a ，其中最小值为双曲线的实轴长；探究一：已知椭圆:C 12222=+by a x ，点F 为椭圆C 的左焦点，直线l 过点F ，交椭圆C 于A 、B 两点，求焦点弦AB 的取值范围； 解：)0,(c F -，设直线l 的倾斜角为α，则直线l 的参数方程为：⎩⎨⎧=+-=ααsin cos t y t c x （t 为参数）， 设点A 、B 对应的参数分别为1t ，2t ，联立直线l 和椭圆C 的方程得：0cos 2)sin cos (4222222=--+b ct b t a b ααα，由韦达定理得：ααα2222221sin cos cos 2a b c b t t +=+，αα2222421sin cos a b b t t +-=， 由弦长公式得：21221214)(t t t t t t AB -+=-=ααααα2222422222224sin cos 4)sin cos (cos 4a b b a b c b +++= ααααααα222222222222224224sin cos 2)sin cos ()sin cos (4cos 4a b ab a b a b b c b +=+++= α2222sin 2c b ab += 所以当0sin 2=α时，焦点弦AB 取最大值，a AB 2max =，即椭圆的长轴长，此时AB l 与x 轴重合；当1sin 2=α时，焦点弦AB 取最小值，ab AB 2min 2=，即椭圆的通经，此时直线x l AB ⊥轴；综上所述：焦点弦⎥⎦⎤⎢⎣⎡∈a a b AB 2,22 结论1：椭圆焦点弦AB 的取值范围为⎥⎦⎤⎢⎣⎡a a b 2,22，其中最小值为椭圆的通经长，最大值为椭圆的长轴长；探究二：已知抛物线C ：px y 22=，点F 为抛物线C 的焦点，直线l 过点F ，交抛物线C 于A 、B 两点，求焦点弦AB 的取值范围；解：)0,2(pF ，设直线l 的倾斜角为α，则直线l 的参数方程为：⎪⎩⎪⎨⎧=+=ααsin cos 2t y t p x （t 为参数）， 设点A 、B 对应的参数分别为1t ，2t ，联立直线l 和抛物线C 的方程得： 0cos 2sin 222=--p pt t αα，由韦达定理得：αα221sin cos 2p t t =+，α2221sin p t t -=， 由弦长公式得：αααα2224222122121sin 2sin 4sin cos 44)(pp p t t t t t t AB =+=-+=-=， 因为直线l 交抛物线C 于A 、B 两点，所以倾斜角0≠α，所以(]1,0sin 2∈α，则[)+∞∈,2p AB ，当1sin 2=α，即x l AB ⊥轴时，取最小值p AB 2min =，即通经长；结论2：抛物线焦点弦AB 的取值范围为[)+∞,2p ，其中最小值为抛物线的通经长；探究三：已知双曲线:C 12222=-by a x ，点F 为双曲线C 的左焦点，直线l 过点F ，交双曲线C 于A 、B 两点，求焦点弦AB 的取值范围； 解：)0,(c F -，设直线l 的倾斜角为α，则直线l 的参数方程为：⎩⎨⎧=+-=ααsin cos t y t c x （t 为参数）， 设点A 、B 对应的参数分别为1t ，2t ，联立直线l 和椭圆C 的方程得：0cos 2)sin cos (4222222=+--b ct b t a b ααα，由韦达定理得：ααα2222221sin cos cos 2a b c b t t -=+，αα2222421sin cos a b b t t -=， 由弦长公式得：21221214)(t t t t t t AB -+=-=ααααα2222422222224sin cos 4)sin cos (cos 4a b b a b c b ---= ααααααα222222222222224224sin cos 2)sin cos ()sin cos (4cos 4a b ab a b a b b c b -=---= α2222sin 2c b ab -= 因为[]1,0sin 2∈α，所以[]0,sin 222c c -∈-α， 所以[]22222,sin b a c b -∈-α，因为直线l 交双曲线C 于A 、B 两点，所以ab±≠αtan ，即0sin 222≠-αc b ，所以[)(]22222,00,sin b a c b -∈-α，（1）若b a ≥，则(]2222,0sin a c b ∈-α，⎪⎭⎫⎢⎣⎡+∞∈,22a b AB ，当1sin 2=α，即直线x l AB ⊥轴时，取最小值ab AB 2min2=，即双曲线的通经；（2）若b a <，则(]2222,0sin b c b ∈-α，[)+∞∈,2a AB ，当0sin 2=α，即AB l 与x 轴重合时，取最大值a AB 2max =，即双曲线的实轴长；结论3：（1）若b a ≥时，双曲线的焦点弦AB 的取值范围为⎪⎭⎫⎢⎣⎡+∞,22a b ，其中最小值为双曲线的通经长； （2）若b a <时，双曲线的焦点弦AB 的取值范围为[)+∞,2a ，其中最小值为双曲线的实轴长；。

专题07 圆锥曲线的第二定义与焦点弦【突破总分值数学之秒杀技巧与答题模板】：焦点弦定义：过焦点的直线与曲线相交于两点A 、B ，弦AB 叫做曲线的焦点弦。

秒杀题型一：椭圆与双曲线焦点弦中常考的秒杀公式：①焦点弦长公式：θ222cos 12e a b -(θ为直线与焦点所在轴的夹角)，通径：22b a (最短焦点弦)； ②焦点弦被焦点分成两局部,m n ，那么2112am n b+=(定值)(取通径即可)。

③BF AF λ=，那么有11cos +-=λλθe (θ为直线与焦点所在轴的夹角)。

秒杀题型二：抛物线的焦点弦中常考的秒杀公式：①过抛物线)0(22>=p px y 焦点的直线交抛物线于A 、B 两点，那么:2p y y B A -=,42p x x B A =。

(焦点在y 轴上的性质比照给出。

)引伸:M (,0)a (0)a >在抛物线22(0)y px p =>的对称轴上，过M 的直线交抛物线于两点。

1122(,),(,)A x y B x y ,12.y y =2pa -(定值)。

②α2sin 2||pAB =(α是直线AB 与焦点所在轴的夹角)=12x x p ++(焦点在x 轴正半轴上)(其它三种同理可以推导)，焦点弦中通径(垂直于对称轴的焦点弦,长为2p )最短。

③BF AF λ=，那么有11cos +-=λλθ，θcos 1-=p AF ，θcos 1+=p BF (θ为直线与焦点所在轴的夹角)。

④面积:θsin 22p S AOB=∆，θ32sin 2p S AMNB =(θ是直线AB 与焦点所在轴的夹角)。

⑤以AB 为直径的圆与准线MN 相切，切点为MN 中点Q ，BQ AQ ,分别是抛物线的切线，并且分别是NBA MAB ∠∠,的角平分线。

⑥以MN 为直径的圆与AB 相切，切点为焦点F 。

⑦以焦半径为直径的圆与y 轴相切。

⑧N O A ,,三点共线,M O B ,,三点共线。

圆锥曲线焦点弦二级结论分类汇总题型1圆锥曲线通径二级结论题型2椭圆焦点弦三角形周长二级结论题型3双曲线焦点弦周长二级结论(同支)题型4双曲线焦点弦周长问题二级结论(不同支)题型5椭圆倾斜角式焦点弦长二级结论题型6双曲线倾斜角式焦点弦长二级结论题型7抛物线倾斜角式焦点弦长二级结论题型8椭圆、双曲线点坐标式焦半径公式二级结论题型9抛物线点坐标式焦半径公式二级结论题型10焦点弦定比分点求离心率二级结论题型1圆锥曲线通径二级结论椭圆，双曲线的通径长AB=2b2 a.1(2022·全国·高三专题练习)过椭圆x2a2+y2b2=1(a>b>0)的焦点F c,0的弦中最短弦长是()A.2b2a B.2a2bC.2c2aD.2c2b【变式训练】1(2021秋·河北邯郸·高三校考阶段练习)已知过椭圆x2a2+y2b2=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为其右焦点，若∠F1PF2=60°，则椭圆的离心率为()A.53B.32C.22D.332(2023秋·四川内江·高三期末)椭圆x24+y23=1的焦点为F1、F2，点M在椭圆上且MF1⊥x轴，则F1到直线F2M的距离为()A.65B.3 C.113D.37113(2022·全国·高三专题练习)过双曲线的一个焦点且与双曲线的实轴垂直的弦叫做双曲线的通径，则双曲线y216-x29=1的通径长是()A.94B.92C.9D.104(2022·全国·高三专题练习)抛物线y2=4x的通径(过抛物线的焦点且与其对称轴垂直的弦)的长为．5(2023·全国·模拟预测)已知抛物线C：x2=2py(p>0)的焦点为F，过F且垂直于y轴的直线与C 相交于A，B两点，若△AOB(O为坐标原点)的面积为18，则p=．6(2023·全国·高三专题练习)过椭圆x29+y2=1的左焦点作直线和椭圆交于A、B两点，且AB=23，则这样直线的条数为()A.0B.1C.2D.3题型2椭圆焦点弦三角形周长二级结论1．F1 , F2为椭圆C:x2a2+y2b2=1a>b>0的左、右焦点，过F1的直线交椭圆于A , B两点，则△ABF2的周长为4a．2.F1, F2为椭圆C:x2a2+y2b2=1a>b>0的左、右焦点，过F2的直线交椭圆于A , B两点，则△ABF1的周长为4a．注意：椭圆的焦点弦三角形周长为定值，即长轴长的2倍，与过焦点的直线的倾斜角无关．1(2022·全国·高三专题练习)如图，椭圆C:x24+y23=1的左焦点为F1，过F1的直线交椭圆于A , B两点，求△ABF2的周长．【变式训练】1在平面直角坐标系xOy中，椭圆C的中心为原点，焦点F1，F2在x轴上，离心率为22，过F1作直线l交C于A,B两点，且ΔABF2的周长为16，那么C的方程为．2椭圆焦点为F1，F2，过F1的最短弦PQ长为10，ΔPF2Q的周长为36，则此椭圆的离心率为()A.33B.13C.23D.633(2022·全国·高三专题练习)已知椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1、F2，短轴长为43，离心率为12，过点F1的直线交椭圆于A,B两点，则△ABF2的周长为()A.4B.5C.16D.324(2020下·四川内江·高三威远中学校校考阶段练习)椭圆E :x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1,F 2，过点F 1的直线交椭圆于A ,B 两点，交y 轴于点C ，若F 1，C 是线段AB 的三等分点，△F 2AB 的周长为45，则椭圆E 的标准方程为()A.x 25+y 24=1B.x 25+y 23=1C.x 25+y 22=1D.x 25+y 2=15(2014·全国·高考真题)已知椭圆C ：x 2a 2+y 2b2=1(a >b >0)的左右焦点为F 1,F 2离心率为33，过F 2的直线l 交C 与A ,B 两点，若△AF 1B 的周长为43，则C 的方程为()A.x 23+y 22=1 B.x 23+y 2=1C.x 212+y 28=1D.x 212+y 24=16古希腊数学家阿基米德用“逼近法”得到椭圆面积的4倍除以圆周率等于椭圆的长轴长与短轴长的积.已知椭圆C 的中心在原点，焦点F 1，F 2在y 轴上，其面积为43π，过点F 1的直线l 与椭圆C 交于点A ，B 且△F 2AB 的周长为16，则椭圆C 的方程为()A.y 216+x 23=1 B.y 216+x 212=1C.x 216+y 212=1D.x 216+y 23=17(2014·安徽·高考真题)设F 1,F 2分别是椭圆E ：x 2a2+y b 22=1(a >b >0)的左、右焦点，过点F 1的直线交椭圆E 于A ,B 两点，|AF 1|=3|BF 1|(1)若|AB |=4,ΔABF 2的周长为16，求|AF 2|；(2)若cos ∠AF 2B =35，求椭圆E 的离心率.8(2022·全国·高三专题练习)已知直线l 经过椭圆C ：x 2a 2+y 2b2=1(a >b >0)的右焦点(1，0)，交椭圆C 于点A ，B ，点F 为椭圆C 的左焦点，△ABF 的周长为8．(1)求椭圆C 的标准方程；(2)若直线m 与直线l 的倾斜角互补，且交椭圆C 于点M ，N ，MN 2=4|AB |，求证：直线m 与直线l 的交点P 在定直线上．题型3双曲线焦点弦周长二级结论(同支)同支问题：F 1 , F 2为双曲线C :x 2a2-y 2b 2=1a >0 , b >0 的左、右焦点，过F 1的直线交双曲线同支于A , B 两点，且AB =m ，则△ABF 2的周长为4a +2m ．证明：由双曲线的第一定义知，AF 2 -AF 1 =2a ①，BF 2 -BF 1 =2a ②，又AF 1 +BF 1 =m ③，由①②③，得AF 2 +BF 2 =4a +m , ∴AB +AF 2 +BF 2 =4a +2m ，即△ABF 2的周长为4a +2m ．1(2022·全国·高三专题练习)椭圆y249+x224=1与双曲线y2-x224=1有公共点P，则P与双曲线两焦点连线构成三角形的周长为．【变式训练】1(2022·全国·高三专题练习)已知双曲线的左、右焦点分别为F1、F2，在左支上过F1的弦AB的长为5，若2a=8，那么△ABF2的周长是()A.26B.21C.16D.52如图双曲线C:x2-y23=1的焦点为F1､F2，过左焦点F1倾斜角为30°的直线l与C交于A,B两点．(1)求弦长AB的值；(2)求△ABF2的周长．3已知双曲线的左、右焦点分别为F1､F2，在左支上F1的弦AB的长为5，若2a=8，那么△ABF2的周长是()A.26B.21C.16D.54如果F1、F2分别是双曲线x216-y29=1的左、右焦点，AB是双曲线左支上过点F1的弦，且|AB|=6，则ΔABF2的周长是5(2022·全国·高三专题练习)若F1,F2分别是双曲线x2m-y27=1的左、右焦点，AB是双曲线左支上过点F1的弦，且|AB|=4，△ABF2的周长是20，则m=．6已知双曲线x 2-y 23=1的左、右焦点分别为F 1，F 2，过F 1作倾斜角为π6的弦AB ．求：(1)AB 的长；(2)△F 2AB 的周长．7已知双曲线C 经过点P 3,2 ，它的两条渐近线分别为x +3y =0和x -3y =0.(1)求双曲线C 的标准方程；(2)设双曲线C 的左､右焦点分别为F 1､F 2，过左焦点F 1作直线l 交双曲线的左支于A ､B 两点，求△ABF 2周长的取值范围.题型4双曲线焦点弦周长问题二级结论(不同支)双曲线异支焦点弦三角形周长【结论3】如图，F 1 , F 2为双曲线C :x 2a2-y 2b 2=1a >0 , b >0 的左、右焦点，过F 2的直线l 与双曲线C 右支、左支分别交于A , B 两点，且AB =m ，则焦点弦三角形F 1AB 的周长：C ΔF 1AB =m +m m +2b 2a．证明：令AF 2 =u , BF 2 =v ，则AF 1 =2a +u , BF 1 =v -2a ，ΔF 1AB 的半周长s =v ，由秦九韶-海伦公式得S ΔFAB =s s -AB s -AF 1 s -BF 1 =2a m -2a uv ．又cos ∠AF 2F 1=cos ∠BF 2F 1，由余弦定理推论，得u 2+4c 2-2a +u 22u ⋅2c =v 2+4c 2-v -2a 22v ⋅2c ，∴b 2-au u =b 2+av v , ∴b 2u -b 2v =2a , ∴uv =b 2v -u 2a =b 2m 2a ，将u =v -m 代入uv =b 2m2a，得v -m v =b 2m 2a ，解这个关于v 的一元二次方程，得v =12m +m m +2b 2a ．又ΔF 1AB 的半周长s =v ，因此异支焦点弦三角形F 1AB 的周长C ΔF 1AB =m +m m +2b 2a．1(2021·浙江·统考一模)如图所示，F 1，F 2是双曲线C ：x 2a2-y 2b 2=1(a >0，b >0)的左、右焦点，过F 1的直线与C 的左、右两支分别交于A ，B 两点．若AB ∶BF 2∶ AF 2 =3∶4∶5，则双曲线的离心率为()A.2B.15C.13D.3【变式训练】1(2021下·安徽安庆·高三校联考阶段练习)已知双曲线x 2a 2-y 2b2=1a >0,b >0 的左、右焦点分别为F 1，F 2，过F 1的直线与双曲线的左、右两支分别交于A ，B 两点，若△ABF 2为边长为4的等边三角形，则△AF 1F 2的面积为()A.23B.33C.43D.632(2021·高三课时练习)已知双曲线C :x 2-y 23=1的右焦点为F ，P 是双曲线C 的左支上一点，M 0,2 ，则△PFM 的周长的最小值为()A.2+42B.4+22C.32D.26+33已知F 1、F 2分别是双曲线x 23-y 26=1的左右焦点，过右焦点F 2作倾斜角为30°的直线交双曲线于A 、B 两点．(Ⅰ)求线段AB 的长；(Ⅱ)求△AF 1B 的周长．题型5椭圆倾斜角式焦点弦长二级结论二级结论1.圆锥曲线的角度式焦半径公式与焦点弦公式设直线l 过圆锥曲线焦点F 且交圆锥曲线于A , B 两点，不妨设AF >BF ，若已知直线l 倾斜角为θ，设圆锥曲线半通径为p =b 2a，则AF =p 1-e cos θ , BF =p 1-e cos θ+π =p 1+e cos θ , ∴AB =AF +BF =2p1-e 2cos 2θ，即圆锥曲线的焦半径公式与焦点弦公式分别为：AF =p 1-e cos θ , BF =p 1+e cos θ , ∴AB =2p1-e 2cos 2θ①.二级结论2.椭圆的倾斜角式焦点弦长公式：(1)F 1 , F 2为椭圆C :x 2a 2+y 2b2=1a >b >0的左、右焦点，过F 1倾斜角为θ的直线l 与椭圆C 交于A , B 两点，则AB =2ab 2a 2-c 2cos 2θ=2p 1-e 2cos 2θp =b 2a；(2)F 1 , F 2为椭圆C :y 2a 2+x 2b2=1a >b >0 的上、下焦点，过F 1倾斜角为θ的直线l 与椭圆C 交于A , B 两点，则AB =2ab 2a 2-c 2sin 2θ=2p 1-e 2sin 2θp =b 2a．说明：特殊情形，当倾斜角为θ=90°时，即为椭圆的通径，通径长AB =2b 2a．圆锥曲线统一的倾斜角式焦点弦长公式：设直线l 过圆锥曲线焦点F 且交圆锥曲线于A , B 两点，若已知直线l 倾斜角为θ，设圆锥曲线通径为2p =2b2a，则圆锥曲线统一的焦点弦长公式：AB =2p1-e 2cos 2θ焦点在x 轴上2p1-e 2sin 2θ焦点在y 轴上．1(2022·全国·高三专题练习)如图，F 1 , F 2为椭圆C :x 2a 2+y 2b2=1a >b >0 的左、右焦点，过F 1倾斜角为θ的直线l 与椭圆C 交于A , B 两点，求弦长AB ．【变式训练】1经过椭圆x 22+y 2=1的左焦点F 1作倾斜角为60°的直线l ，直线l 与椭圆相交于A ，B 两点，求AB的长.2(2022上·全国·高二专题练习)已知椭圆x 2a 2+y 2b2=1(a >b >0)的离心率为33，过椭圆的右焦点且斜率为12的直线与椭圆交于A ，B 两点，则△AOB (其中O 为原点)的形状为.3(2022上·全国·高三专题练习)椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别是F 1,F 2，斜率为12的直线l 过左焦点F 1且交C 于A ，B 两点，且△ABF 2的内切圆的周长是2π，若椭圆的离心率为e ∈12,34，则线段AB 的长度的取值范围是4(2022·全国·高三专题练习)过椭圆3x 2+4y 2=48椭圆的左焦点引直线交椭圆于A ，B 两点，|AB |=7，求直线方程．5(2022·全国·高三专题练习)已知椭圆x 29+y 28=1的左右焦点分别为F 1 , F 2，若过点P 0，-2 及F 1 的直线交椭圆于A ，B 两点，求△ABF 2的面积.6(2023·四川广安·统考模拟预测)已知抛物线C :y 2=2px p >0 的焦点F 与椭圆x 225+y 216=1的右焦点重合．斜率为k k >0 直线l 经过点F ，且与C 的交点为A ，B ．若AF =3BF ，则直线l 的方程是()A.3x -y -33=0B.43x -4y -33=0C.3x -y -9=0D.x -3y -3=0题型6双曲线倾斜角式焦点弦长二级结论二级结论：曲线的倾斜角式焦点弦长公式：(1)F 1 , F 2为双曲线C :x 2a2-y 2b 2=1a >0 , b >0 的左、右焦点，过F 1倾斜角为θ的直线l 与双曲线C 交于A , B 两点，则AB =2ab 2a 2-c 2cos 2θ =2p 1-e 2cos 2θ p =b 2a ．(2)F 1 , F 2为双曲线C :y 2a2-x 2b 2=1a >0 , b >0 的上、下焦点，过F 1倾斜角为θ的直线l 与双曲线C 交于A , B 两点，则AB =2ab 2a 2-c 2sin 2θ =2p 1-e 2sin 2θ p =b 2a ．说明：特殊情形，当倾斜角为θ=90°时，即为双曲线的通径，通径长2p =2b 2a．圆锥曲线统一的倾斜角式焦点弦长公式：设直线l 过圆锥曲线焦点F 且交圆锥曲线于A , B 两点，若已知直线l 倾斜角为θ，设圆锥曲线通径为2p =2b2a，则圆锥曲线统一的焦点弦长公式：AB =2p1-e 2cos 2θ焦点在x 轴上2p1-e 2sin 2θ焦点在y 轴上．1(2022·全国·高三专题练习)设双曲线x 2a2-y 2b 2=1a >0 , b >0 ，其中两焦点坐标为F 1-c ,0 F 2c ,0 ，过F 1的直线l 的倾斜角为θ，交双曲线于A ，B 两点，求弦长AB ．【变式训练】1(2022·全国·高三专题练习)过双曲线x 24-y 28=1的右焦点F 作倾斜角为45°的直线，交双曲线于A , B 两点，求弦长AB ．2(2022·全国·高三专题练习)过双曲线x 2-y 2=4的右焦点F 作倾斜角为150°直线，交双曲线于A , B 两点，求弦长AB ．3(2022·全国·高三专题练习)过双曲线x 24-y 28=1的右焦点F 作倾斜角为45°的直线，交双曲线于A , B 两点，求弦长AB ．4(2022·全国·高三专题练习)过双曲线x 2-y 2=4的右焦点F 作倾斜角为30°的直线，交双曲线于A 、B 两点，求弦长AB ．5(2022·全国·高三专题练习)已知双曲线x 23-y 22=1的左右焦点分别为F 1，F 2，若过点P (0，-2)及F 1的直线交双曲线于A ，B 两点，求△ABF 2的面积题型7抛物线倾斜角式焦点弦长二级结论二级结论：1.抛物线的焦点弦长：AB =2psin 2θ焦点在x 轴上2pcos 2θ焦点在y 轴上．2.过抛物线y 2=2px (p >0)焦点的直线交抛物线于A ,B 两点，则：y A y B =-p 2,x A x B =p 24.(焦点在y 轴上的性质对比给出.)引伸：M (a ,0)(a >0)在抛物线y 2=2px (p >0)的对称轴上，过M 的直线交抛物线于两点.A x 1,y 1 ,B x 2,y 2 ,y 1,y 2=-2pa (定值).3.|AB |=2p sin 2α(α是直线AB 与焦点所在轴的夹角)=x 1+x 2+p (焦点在cos θ =λ-1λ+1 轴正半轴上)(其它三种同理可以推导)，焦点弦中通径(垂直于对称轴的焦点弦，长为2p )最短.4.AF =λBF ，则有cos θ|=|λ-1λ+1|,AF =p 1-cos θ，BF =p 1+cos θ(θ为直线与焦点所在轴的夹角).1(2022·全国·高三专题练习)如图，抛物线y 2=2px p >0 与过焦点F p2,0的直线l 相交于A ,B 两点，若l 的倾斜角为θ，求弦长AB ．【变式训练】1(2020·山东·统考高考真题)斜率为3的直线过抛物线C ：y 2=4x 的焦点，且与C 交于A ，B 两点，则AB =．2已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1,l 2，直线l 1与C 交于A ,B 两点，直线l 2与C 交于D ,E 两点，则AB +DE 的最小值为()A.16B.14C.12D.103(2021上·江西·高三校联考阶段练习)过抛物线y 2=2px p >0 的焦点F 作倾斜角为θθ≠π2的直线，交抛物线于A ,B 两点，当θ=π3时，以FA 为直径的圆与y 轴相切于点T 0,3 .(1)求抛物线的方程；(2)试问在x 轴上是否存在异于F 点的定点P ，使得FA ⋅PB =FB ⋅PA 成立？若存在，求出点P 的坐标，若不存在，请说明理由.4(2020·四川遂宁·统考二模)过抛物线y 2=2px p >0 的焦点F 作直线交抛物线于M ，N 两点(M ，N 的横坐标不相等)，弦MN 的垂直平分线交x 轴于点H ，若MN =40，则HF =()A.14B.16C.18D.205设抛物线C :y 2=4x 的焦点为F ，直线l 过F 且与C 交于A , B 两点.若|AF |=3|BF |，则l 的方程为()A.y =x -1或y =-x +1B.y =33(X -1)或y =-33(x -1)C.y =3(x -1)或y =-3(x -1)D.y =22(x -1)或y =-22(x -1)6(2022·全国·高三专题练习)已知点F 和直线l 是离心率为e 的双曲线C 的焦点和对应准线，焦准距(焦点到对应准线的距离)为p ．过点F 的弦AB 与曲线C 的焦点所在的轴的夹角为θ0°<θ≤90° ，则有．题型8椭圆、双曲线点坐标式焦半径公式二级结论一．椭圆的焦半径及其应用：1.焦半径公式：Px 0，y 0是椭圆x 2a2+y 2b 2=1(a >b >0)上一点，F 1 , F 2是左、右焦点，e 椭圆的离心率是则,PF 1=a +ex 0,PF 2=a -ex 0，Px 0，y 0是椭圆y 2a2+x 2b 2=1(a >b >0)上一点，F 1 , F 2是上、下焦点，e 椭圆的离心率是则,PF 1=a -ey 0,PF 2=a +ey 0，2.椭圆的坐标式焦点弦长公式：(1)椭圆x 2a2+y 2b 2=1(a >b >0)的焦点弦长公式：AB =2a +e x A +x B (过左焦点)；AB =2a -e x A +x B (过右焦点)，即AB =2a -e x A +x B ；(2)椭圆y 2a 2+x 2b2=1(a >b >0)的焦点弦长公式：AB =2a -e y A +y B (过上焦点)；AB =2a +e y A +y B (过下焦点)，即AB =2a -e y A +y B ．二．双曲线的焦半径及其应用：1:定义：双曲线上任意一点M 与双曲线焦点的连线段，叫做双曲线的焦半径.2.当点P 在双曲线上时的焦半径公式，(其中F 1 为左焦点，F 2为右焦点)它是由第二定义导出的，其中a 是实半轴长，e 是离心率，x 0是P 点的横坐标.当焦点在x 轴，P 在左支时：PF 1=-(ex 0+a ),PF 2=-(ex 0-a ).当焦点在x 轴，P 在右支时：PF 1=ex 0+a ,PF 2=ex 0-a .当焦点在y 轴:P 在上支时：PF 1=ey 0+a ,PF 2=ey 0-a当焦点在y轴:P在下支时：PF1=-(ey0+a),PF2=-(ey0-a)三．双曲线的坐标式焦点弦长公式：(1)双曲线x2a2-y2b2=1a>0 , b>0的焦点弦长公式：同支弦AB=e x A+x B-2a=2ab21+k2a2k2-b2；异支弦AB=2a-e x A+x B=2ab21+k2b2-a2k2，统一为：AB=e x A+x B-2a =2ab21+k2a2k2-b2；(2)双曲线y2a2-x2b2=1a>0 , b>0的焦点弦长公式：同支弦AB=e y A+y B-2a；异支弦AB=2a-e y A+y B，统一为：AB=e y A+y B-2a．1(2022·全国·高三专题练习)已知椭圆x2a2+y2b2=1a>b>0，若过左焦点的直线交椭圆于A , B两点，求AB．【变式训练】1(2022·全国·高三专题练习)已知椭圆x22+y21=1的左右焦点分别为F1，F2，若过点P0,-2及F1的直线交椭圆于A，B两点，求AB．2(2022·全国·高三专题练习)已知椭圆x249+y213=1，若过左焦点的直线交椭圆于A，B两点，且A，B两点的横坐标之和是-7，求AB．3(2022·全国·高三专题练习)设双曲线x2a2-y2b2=1(a>0,b>0)，其中两焦点坐标为F1(-c,0),F2(c,0)，经过右焦点的直线交双曲线于A、B两点，求弦长|AB|．题型9抛物线点坐标式焦半径公式二级结论抛物线的坐标式焦点弦长公式：(1)抛物线y2=2px p>0的焦点弦长公式：AB=p+x A+x B；(2)抛物线y2=-2px p>0的焦点弦长公式：AB=p-x A+x B；(3)抛物线x2=2py p>0的焦点弦长公式：AB=p+y A+y B；(4)抛物线x2=-2py p>0的焦点弦长公式：AB=p-y A+y B．1(2021·河北·高三专题练习)过抛物线y2=2px p>0的焦点F作倾斜角为45°的直线交抛物线于A,B两点，若线段AB的长为8，则P=.【变式训练】1(2023·北京·人大附中校考三模)已知抛物线y2=2px(p>0)的焦点为F，过点F的直线与该抛物线交于A，B两点，AB=10，AB的中点横坐标为4，则p=．2(2023·全国·模拟预测)已知抛物线C:y2=4x的焦点为F，则过点F且斜率为3的直线l截抛物线C所得弦长为()A.223B.163C.193D.833题型10焦点弦定比分点求离心率二级结论1.点F 是椭圆的焦点，过F 的弦AB 与椭圆焦点所在轴的夹角为θ,θϵ0,π2，k 为直线AB 的斜率，且AF =λFB (λ>0)，则e =1+k 2λ-1λ+1当曲线焦点在y 轴上时，e =1+1k 2λ-1λ+1注：λ=AF BF 或者λ=BF AF ,而不是AF AB 或者BFAB点F 是双曲线焦点，2.过F 弦AB 与双曲线焦点所在轴夹角为θ,θϵ0,π2，k 为直线AB 斜率，且AF =λFB (λ>0)，则e =1+k 2λ-1λ+1当曲线焦点在y 轴上时，e =1+1k 2λ-1λ+1 1(23·24高三上·云南·阶段练习)已知椭圆C ：x 2a2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1，F 2，过点F 2且倾斜角为60°的直线l 与C 交于A ，B 两点．若△AF 1F 2的面积是△BF 1F 2面积的2倍，则C 的离心率为．【变式训练】1(2022上·辽宁鞍山·高三鞍山一中校考期中)已知椭圆C :x 2a 2+y 2b2=1的左焦点为F ，过F 斜率为3的直线l 与椭圆C 相交于A 、B 两点，若AF BF =32，则椭圆C 的离心率e =．2(2022·全国·高三专题练习)已知双曲线C :x 2a 2-y 2b2=1a >0,b >0 的右焦点为F ，过F 且斜率为3的直线交C 于A 、B 两点，若AF =4FB，则C 的离心率为()A.58B.65C.75D.953(2022·全国·高三专题练习)已知椭圆x 2a 2+y 2b 2=1(a >b >0)的右焦点为F ，经过F 且倾斜角为60°的直线l 与椭圆相交于不同两点A ,B ，已知AF =2FB．(1)求椭圆的离心率；(2)若|AB |=154，求椭圆方程．4(2023·贵州·统考模拟预测)椭圆C :x 2a 2+y 2b2=1(a >b >0)的上顶点为A ,F 是C 的一个焦点，点B 在C 上，若3AF +5BF =0，则C 的离心率为()A.12B.35C.22D.321(2023·浙江温州·乐清市知临中学校考二模)已知椭圆x 2a 2+y 2b2=1的右焦点为F 2，过右焦点作倾斜角为π3的直线交椭圆于G ,H 两点，且GF 2 =2F 2H ，则椭圆的离心率为()A.12B.22C.23D.322(2022·全国·高三专题练习)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的离心率为433，过左焦点F 且斜率为k >0的直线交C 的两支于A ,B 两点．若|FA |=3|FB |，则k =．3(多选)(2022·辽宁沈阳·统考模拟预测)已知双曲线x 2a 2-y 2b2=1a >0,b >0 的离心率为e ，左、右焦点分别为F 1、F 2，过点F 2的直线与双曲线右支交于P ，Q 两点，且PF 1 =2PF 2 ，下列说法正确的是()A.PF 2 与双曲线的实轴长相等B.e ∈1,3C.若P 在以F 1F 2为直径的圆上，则双曲线的渐近线方程为y =±4xD.若PF 1 =QF 2 ，则直线PQ 的斜率为±424(2021·四川成都·石室中学校考三模)已知直线经过抛物线y 2=2px p >0 的焦点F 并交抛物线于A ，B 两点，则AF =4，且在抛物线的准线上的一点C 满足CB =2BF，则p =.5(2020·全国·校联考模拟预测)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)过点M (3,1)，且左、右顶点分别为A 1,A 2，左焦点为F 1，上、下两个顶点分别为B 1,B 2,0为坐标原点，△A 1B 1F 1与△OA 2B 2面积的比值为3-63．(1)求C 的标准方程；(2)过F 1且斜率为k k >0 的直线l 与椭圆C 交于P ,Q 两点，点D 在y 轴上，且满足PD =QD ，已知E (0,-2)，求△EPQ 与△A 2OD 面积比值的最小值．6(2021·江西新余·统考模拟预测)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)和圆O :x 2+y 2=a 2,F 1(-1,0),F 2(1,0)分别是椭圆的左、右两焦点，过F 1且倾斜角为α∈0,π2的动直线l 交椭圆C 于A ,B 两点，交圆O 于P ,Q 两点(如图所示)，当α=π4时，弦PQ 的长为14．(1)求圆O 和椭圆C 的方程(2)若点M 是圆O 上一点，求当AF 2,BF 2,AB 成等差数列时，△MPQ 面积的最大值．7(2020·安徽蚌埠·统考一模)已知M 是椭圆C ：x 2a 2+y 2b2=1(a >b >0)上一点，F 1、F 2分别为椭圆C 的左、右焦点，且F 1F 2 =2，∠F 1MF 2=π3，△F 1MF 2的面积为3．(1)求椭圆C 的方程；(2)直线l 过椭圆C 右焦点F 2，交该椭圆于A 、B 两点，AB 中点为Q ，射线OQ (O 为坐标原点)交椭圆于P ，记△AOQ 的面积为S 1，△BPQ 的面积为S 2，若S 2=3S 1，求直线l 的方程．8(2010·全国·高考真题)已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C于点D ，且BF =2FD，则C 的离心率为9(2010·全国·高考真题)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的离心率为32，过右焦点F 且斜率为k (k >0)的直线与C 相交于A 、B 两点．若AF =3FB，则k =()A.1B.2C.3D.210(2009·全国·高考真题)已知双曲线C :χ2a 2-y 2b2=1(a >0，b >0)的右焦点为F 且斜率为3的直线交C 于A 、B 两点，若AF =4FB，则C 的离心率为()A.65B.75C.85D.9511(2023·全国·统考高考真题)(多选)设O 为坐标原点，直线y =-3x -1 过抛物线C :y 2=2px p >0 的焦点，且与C 交于M ，N 两点，l 为C 的准线，则()．A.p =2B.MN =83C.以MN 为直径的圆与l 相切D.△OMN 为等腰三角形。

（ ）由题 意及定 理 ３得 Ｉ 引 ＝ ２ Ａ
一 ＝
等 ＝
．
一一一来自０ ｂ＞０ ， ）焦点 Ｆ且倾 斜角 为 Ｏ 的直线 ， 曲线 的离 ｌ 双 心率 为 ｅ 则有 ， （ ）当直线 ｆ １ 与双 曲线 的两个 交点 Ｐ， ９在双 曲
１
例２２ ６ 考福 （ ０年高 建理科 双曲 － 一 ０ 卷） 线口 号 － Ｄ ５ －
＝１ａ＞０ ｂ＞０ 右焦点是 ， Ｆ且倾斜角为６ 。 （ ， ） 过 ｏ
１
焦 点 弦端 点 的分 布 问题 ， 反 映焦 点 弦端 点 的 是
分 布位置 与 圆锥 曲线 离 心率 范 围 之 间 的 内在联 系 ，
此类 问题 可将其 归纳 出如下 结论． 定理 １ Ｐ， Ｑ是 经过椭 圆 ｂｘ ２ ＋Ⅱｙ Ｚ＝ａｂ （ ２ ａ
（ ）因为 Ｐ， 双 曲线 的异 支上 ， ２ Ｑ在 由渐 近 线斜 率与 弦 ｅ Ｑ的斜率 的关 系知 ｌ ａ ｏＩ＜ ｂ￣ｔｎ ＜ ｎｔ ｔ ａ
证明 ： 由对称性 ， 不妨 设 Ｆ为 右焦点 （ ， ） ｃ０ ． （ ）由 题 意 知 ｌｔｎ Ｉ＞ ｂ ￣ｔｎ ＞ １ ａ ａ
Ｃ
， ｔ２
（ ）因为直线 Ｚ ３ 与双 曲线有且 只 有一个 交点 ， 且
ｚ 经过双 曲线 的焦 点 ， 以直线 ｚ 所 于双 曲线 的渐 近 线
ｌ ２
中 学 数 学 研 究
２ １ 年 第 ６期 ０１
高 考 焦 点 弦 问题 的 分 类 解 析
云 南 省广 南县 第 一 中 学 （６ ３ ０ 玉 邴 图（ 级教 师 ） ６３ ０ ） 特
经 过 圆锥 曲线 焦 点 且 被 圆锥 曲线 截 得 的线 段 叫做 圆锥 曲线 焦 点 弦 ．它 是 一 个 非 常 重 要 的 几 何