编译原理答案第二章

第2章形式语言基础2.2 设有文法G[N]: N -> D | NDD -> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9(1)G[N]定义的语言是什么?(2)给出句子0123和268的最左推导和最右推导。

解答：(1)L(G[N])={(0|1|2|3|4|5|6|7|8|9)+} 或L(G[N])={α| α为可带前导0的正整数}(2)0123的最左推导：N ⇒ ND ⇒ NDD ⇒ NDDD ⇒ DDDD ⇒ 0DDD ⇒ 01DD ⇒ 012D ⇒ 0123 0123的最右推导：N ⇒ ND ⇒ N3 ⇒ ND3 ⇒ N23 ⇒ ND23 ⇒ N123 ⇒ D123 ⇒ 0123268的最左推导：N ⇒ ND ⇒ NDD ⇒ DDD ⇒ 2DDD ⇒ 26D ⇒ 268268的最右推导：N ⇒ ND ⇒ N8 ⇒ ND8 ⇒ N68 ⇒ D68 ⇒ 2682.4 写一个文法，使其语言是奇数的集合，且每个奇数不以0开头。

解答：首先分析题意，本题是希望构造一个文法，由它产生的句子是奇数，并且不以0开头，也就是说它的每个句子都是以1、3、5、7、9中的某个数结尾。

如果数字只有一位，则1、3、5、7、9就满足要求，如果有多位，则要求第1位不能是0，而中间有多少位，每位是什么数字（必须是数字）则没什么要求，因此，我们可以把这个文法分3部分来完成。

分别用3个非终结符来产生句子的第1位、中间部分和最后一位。

引入几个非终结符，其中，一个用作产生句子的开头，可以是1－9之间的数，不包括0，一个用来产生句子的结尾，为奇数，另一个则用来产生以非0整数开头后面跟任意多个数字的数字串，进行分解之后，这个文法就很好写了。

N -> 1 | 3 | 5 | 7 | 9 | BNB -> 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | B02.7 下面文法生成的语言是什么？G1：S->ABA->aA| εB->bc|bBc G2：S->aA|a A->aS解答：B ⇒ bcB ⇒ bBc⇒ bbccB ⇒ bBc⇒ bbBcc ⇒ bbbccc……A ⇒εA ⇒ aA ⇒ aA ⇒ aA ⇒ aaA ⇒ aa……∴S ⇒ AB ⇒ a m b n c n , 其中m≥0,n≥1即L(G1)={ a m b n c n | m≥0,n≥1} S ⇒ aS ⇒ aA ⇒ aaS ⇒ aaaS ⇒ aA ⇒ aaS ⇒ aaaA ⇒aaaaS ⇒ aaaaa ……∴S ⇒ a2n+1 , 其中n≥0即L(G2)={ a2n+1 | n≥0}2.11 已知文法G[S]: S->(AS)|(b)A->(SaA)|(a)请找出符号串(a)和(A((SaA)(b)))的短语、简单短语和句柄。

第二章 高级语言及其语法描述4．令+、*和↑代表加，乘和乘幂，按如下的非标准优先级和结合性质的约定，计算1+1*2↑2*1↑2的值：（1） 优先顺序（从高至低）为+，*和↑，同级优先采用左结合。

（2） 优先顺序为↑，+，*，同级优先采用右结合。

解：（1）1+1*2↑2*1↑2=2*2↑1*1↑2=4↑1↑2=4↑2=16 （2）1+1*2↑2*1↑2=1+1*2*1=2*2*1=2*2=46．令文法G6为 N →D|NDD →0|1|2|3|4|5|6|7|8|9 （1） G6 的语言L （G6）是什么？（2） 给出句子0127、34和568的最左推导和最右推导。

解：（1）L （G6）=｛a|a ∈∑+,∑=﹛0,1,2,3,4,5,6,7,8,9｝｝（2）N ＝＞ND ＝＞ NDD ＝＞ NDDD ＝＞ DDDD ＝＞ 0DDD ＝＞ 01DD ＝＞ 012D ＝＞ 0127 N ＝＞ ND ＝＞ N7＝＞ ND7＝＞ N27＝＞ ND27＝＞ N127＝＞ D127＝＞ 0127 N ＝＞ ND ＝＞ DD ＝＞ 3D ＝＞ 34 N ＝＞ ND ＝＞ N4＝＞ D4 ＝＞34N ＝＞ ND ＝＞ NDD ＝＞ DDD ＝＞ 5DD ＝＞ 56D ＝＞ 568 N ＝＞ ND ＝＞ N8＝＞ ND8＝＞ N68＝＞ D68＝＞ 5687．写一个文法，使其语言是奇数集，且每个奇数不以0开头。

解：A →SN, S →+|-|∑, N →D|MDD →1|3|5|7|9, M →MB|1|2|3|4|5|6|7|8|9 B →0|1|2|3|4|5|6|7|8|9 8. 文法：E T E T E T TF T F T F F E i→+-→→|||*|/()| 最左推导:E E T T TF T i T i T F i F F i i F i i i E T T F F F i F i E i E T i T T i F T i i T i i F i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+********()*()*()*()*()*()*()最右推导:E E T E TF E T i E F i E i i T i i F i i i i i E T F T F F F E F E T F E F F E i F T i F F i F i i i i i ⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒+⇒⇒⇒⇒⇒+⇒+⇒+⇒+⇒+⇒+⇒+**********()*()*()*()*()*()*()*()语法树：/********************************EE FTE +T F F T +iiiEEFTE-T F F T -iiiEEFT+T F FTiii*i+i+ii-i-ii+i*i*****************/9．证明下面的文法是二义的：S → iSeS|iS|I解：因为iiiiei 有两种最左推导，所以此文法是二义的。

第二章 词法分析2.1 完成下列选择题：(1) 词法分析器的输出结果是。

a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。

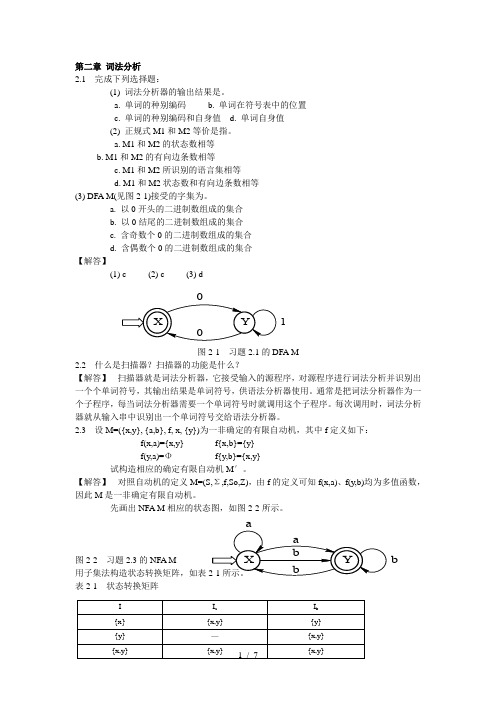
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。

a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器？扫描器的功能是什么？【解答】 扫描器就是词法分析器，它接受输入的源程序，对源程序进行词法分析并识别出一个个单词符号，其输出结果是单词符号，供语法分析器使用。

通常是把词法分析器作为一个子程序，每当词法分析器需要一个单词符号时就调用这个子程序。

每次调用时，词法分析器就从输入串中识别出一个单词符号交给语法分析器。

2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机，其中f 定义如下：f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。

【解答】 对照自动机的定义M=(S,Σ,f,So,Z)，由f 的定义可知f(x,a)、f(y,b)均为多值函数，因此M 是一非确定有限自动机。

先画出NFA M 相应的状态图，如图2-2所示。

图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵，如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名，形成表2-2所示的状态转换矩阵，即得到 M ′=({0,1,2},{a,b},f,0,{1,2})，其状态转换图如图2-3所示。

表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。

第二章 文法和语言p48 4、6（6）、11、 12（2）（6）、18（2）4 证明文法G=（{E,O}，{(，)，+，*，v ，d}，P ，E ）是二义的,其中P 为 E → EOE | (E) | v | d O → + | * 证明：因为E=〉 EOE EOE = =〉EOEOE EOEOE==〉EOEOv EOEOv = =〉EOE+v=〉EOv+v EOv+v==〉E*v+v E*v+v = =〉v*v+v ， 句子v*v+v 有两棵不同的语法树所以文法G 是二义的。

问题：1）只有文字说明，比如v*v+v 有两棵语法树，但没有画出语法树或者最左（最右）推导过程2）给出的是不同句子（v*v+d v+v*d ）的语法树 6、已知文法G ：E E EE E OO v*v+ vE E E E E O O v+v* v〈表达式〉∷=〈项〉|〈表达式〉+〈项〉〈项〉 ∷=〈因子〉|〈项〉*〈因子〉〈因子〉 ∷=（〈表达式〉）| i试给出下述表达式的推导及语法树（6）i+i*i推导过程：〈表达式〉=〉〈表达式〉+〈项〉 E=〉E+T =〉〈表达式〉+〈项〉*〈因子〉 =〉E+ T*F=〉〈表达式〉+〈项〉* i =〉E+ T*i=〉〈表达式〉+ 〈因子〉* i =〉E+F*i=〉〈表达式〉+ i* i =〉E+i*i=〉〈项〉+ i* i =〉T +i*i=〉〈因子〉+ i* i =〉F +i*i=〉i +i*i =〉i +i*i 共8步推导语法树：〈表达式〉〈表达式〉+〈因子〉 〈项〉i 〈因子〉i〈项〉〈项〉 〈因子〉i*11、一个上下文无关文法生成句子abbaa 的推导树如下：（1）给出该句子相应的最左推导和最右推导 （2）该文法的产生式集合P 可能有哪些元素？ （3）找出该句子的所有短语、简单短语、句柄。

（1）最左推导：S=〉ABS=〉aBS=〉aSBBS=〉aBBS =〉abBS=〉abbS =〉abbAa=〉abbaa最右推导：S =〉ABS=〉ABAa=〉ABaa=〉ASBBaa =〉ASBbaa=〉ASbbaa=〉Abbaa=〉abbaa（2）该文法的产生式集合P 可能有下列元素：S →ABS | Aa|e A →a B →SBB|bSABSS B B a 1 a 3b 2 b 1 eAa 2（3）因为字符串中的各字符有相对的位置关系，为了能相互区别，给相同的字符标上不同的数字。

第二章高级语言的语法描述6、令文法G 6为：N →D|ND D → 0|1|2|3|4|5|6|7|8|9（1）G 6 的语言L （G 6）是什么？（2）给出句子01270127、、34和568的最左推导和最右推导。

解答：思路：由N N →→ D|ND 可得出如下推导N ＝＞＝＞ND ND ND＝＞＝＞＝＞NDD NDD NDD＝＞…＝＞＝＞…＝＞＝＞…＝＞D D n（n ＞=1=1））可以看出，N 最终可以推导出1个或多个（也可以是无穷）D ，而D D →→ 0|1|2|3|4|5|6|7|8|9可知，每个D 为0～9中的任一个数字，所以，中的任一个数字，所以，N N N 最终推导出的就是由最终推导出的就是由0～9这10个数字组成的字符串。

（1）G 6 的语言L （G 6）是由0～9这10个数字组成的字符串个数字组成的字符串,,或{0{0，，1,1,……,9}+。

(2)(2)句子句子01270127、、34和568的最左推导分别为的最左推导分别为: : N ＝＞＝＞ND ND ND＝＞＝＞＝＞NDD NDD NDD＝＞＝＞＝＞NDDD NDDD NDDD＝＞＝＞＝＞DDDD DDDD DDDD＝＞＝＞＝＞0DDD 0DDD 0DDD＝＞＝＞＝＞01DD 01DD 01DD＝＞＝＞＝＞012D 012D 012D＝＞＝＞＝＞0127 0127 N ＝＞＝＞ND ND ND＝＞＝＞＝＞DD DD DD＝＞＝＞＝＞3D 3D 3D＝＞＝＞＝＞34 34N ＝＞＝＞ND ND ND＝＞＝＞＝＞NDD NDD NDD＝＞＝＞＝＞DDD DDD DDD＝＞＝＞＝＞5DD 5DD 5DD＝＞＝＞＝＞56D 56D 56D＝＞＝＞＝＞568 568 句子01270127、、34和568的最右推导分别为的最右推导分别为: :N ＝＞＝＞ND ND ND＝＞＝＞＝＞N7N7N7＝＞＝＞＝＞ND7ND7ND7＝＞＝＞＝＞N27N27N27＝＞＝＞＝＞ND27ND27ND27＝＞＝＞＝＞N127N127N127＝＞＝＞＝＞D127D127D127＝＞＝＞＝＞0127 0127 N ＝＞＝＞ND ND ND＝＞＝＞＝＞N4N4N4＝＞＝＞＝＞D4D4D4＝＞＝＞＝＞34 34N ＝＞＝＞ND ND ND＝＞＝＞＝＞N8N8N8＝＞＝＞＝＞ND8ND8ND8＝＞＝＞＝＞N68N68N68＝＞＝＞＝＞D68D68D68＝＞＝＞＝＞568 5687、写一个文法，使其语言是奇数集，且每个基数不以0开头。

第2章习题解答1.文法G[S]为：S->Ac|aBA->abB->bc写出L(G[S])的全部元素[答案]S=>Ac=>abc或S=>aB=>abc所以L(G[S])={abc}2.文法G[N]为：N->D|NDD->0|1|2|3|4|5|6|7|8|9G[N]的语言是什么？[答案]G[N]的语言是V。

V={0,1,2,3,4,5,6,7,8,9}N=>ND=>NDD.... =>NDDDD...D=>D……D3.已知文法G[S]:Sf dAB Af aA|a B|bB问：相应的正规式是什么？G[S]能否改写成为等价的正规文法? [答案]正规式是daa*b* ；相应的正规文法为(由自动机化简来):G[S]:S —dA A —a|aB B —aB|a|b|bC C —bC|b也可为(观察得来):G[S]:S —dA A —a|aA|aB B —bB| &4.已知文法G[Z]:Z->aZb|ab写出L(G[Z])的全部元素。

[答案]Z=>aZb=>aaZbb=>aaa..Z...bbb=> aaa..ab...bbbL(G[Z])={a n b n|n>=1}5.给出语言｛a n b n c1 n>=1,m>=0｝的上下文无关文法。

［分析］本题难度不大，主要是考上下文无关文法的基本概念。

上下文无关文法的基本定义是：A-> B ,A € Vn ,B€( VnU Vt) *,注意关键问题是保证a n b n的成立，即“ a与b的个数要相等”，为此，可以用一条形如A->aAb|ab的产生式即可解决。

［答案］构造上下文无关文法如下：S->AB|AA->aAb|abB->Bc|c［扩展］凡是诸如此类的题都应按此思路进行，本题可做为一个基本代表。

基本思路是这样的：要求符合a n b n c m，因为a与b要求个数相等，所以把它们应看作一个整体单元进行，而c m做为另一个单位，初步产生式就应写为S->AB,其中A推出a n b n，B推出c m。

编译原理习题参考答案第⼆章2.构造产⽣下列语⾔的⽂法（2）{a n b m c p|n,m,p≥0}解： G(S) ：S→aS|X,X→bX|Y,Y→cY|ε（3）{a n # b n|n≥0}∪{cn # dn|n≥0}解： G(S)：S→X,S→Y,X→aXb|#, Y→cYd|# }（5）任何不是以0 打头的所有奇整数所组成的集合解：G(S)：S→J|IBJ,B→0B|IB|ε,I→J|2|4|6|8, J→1|3|5|7|9}（6）（思考题）所有偶数个0 和偶数个1 所组成的符号串集合解：对应⽂法为 S→0A|1B|ε，A→0S|1C B→0C|1S C→1A|0B3.描述语⾔特点（2）S→SS S→1A0 A→1A0 A→ε解：L(G)={1n10n11n20n2… 1nm0nm |n1,n2,…,nm≥0；且n1,n2,…nm 不全为零}该语⾔特点是：产⽣的句⼦中，0、1 个数相同，并且若⼲相接的1 后必然紧接数量相同连续的0。

（5）S→aSS S→a解：L(G)={a(2n-1)|n≥1}可知：奇数个a5. (1) 解：由于此⽂法包含以下规则：AA→ε，所以此⽂法是0 型⽂法。

7.解：(1)aacb 是⽂法G[S]中的句⼦，相应语法树是：最右推导：S=>aAcB=>aAcb=>aacb最左推导：S=>aAcB=>aacB=>aacb（3）aacbccb 不是⽂法G[S]中的句⼦aacbccb 不能从S推导得到时，它仅是⽂法G[S]的⼀个句型的⼀部分，⽽不是⼀个句⼦。

11.解：最右推导:(1) S=>AB=>AaSb=>Aacb=>bAacb=>bbAacb=>bbaacb上⾯推导中，下划线部分为当前句型的句柄。

对应的语法树为：3 假设M:⼈ W:载狐狸过河，G:载⼭⽺过河，C:载⽩菜过河6 根据⽂法知其产⽣的语⾔是L={a m b n c i| m,n,i≧1}可以构造如下的⽂法VN={S,A,B,C}, VT={a,b,c}P={ S →aA, A→aA, A→bB, B→bB, B→cC, C→cC, C→c} 其状态转换图如下:7 (1) 其对应的右线性⽂法是:A →0D, B→0A,B→1C,C→1|1F,C→1|0A,F→0|0E|1A,D→0B|1C,E→1C|0B(2) 最短输⼊串011(3) 任意接受的四个串： 011,0110,0011,000011(4) 任意以1 打头的串.9．对于矩阵(iii)(1) 状态转换图：(2) 3型⽂法（正规⽂法）S→aA|a|bB A→bA|b|aC|a B→aB|bC|b C→aC|a|bC|b(3)⽤⾃然语⾔描述输⼊串的特征以a 打头，中间有任意个（包括0个）b,再跟a,最后由⼀个a,b 所组成的任意串结尾或者以b 打头，中间有任意个（包括0个）a,再跟b,最后由⼀个a,b 所组成的任意串结尾。