二重积分的概念与性质教案

二重积分的概念与性质教案教案：二重积分的概念与性质一、教学目标1.理解二重积分的概念和性质；2.掌握计算二重积分的方法。

二、教学内容1.二重积分的概念；2.二重积分的性质；3.计算二重积分的方法。

三、教学步骤Step 1 导入 (5分钟)通过问题引入二重积分的概念：有一个区域D，如何计算这个区域上的一些函数f(x,y)的平均值？Step 2 二重积分的概念 (15分钟)1.定义：二重积分是对二元函数f(x,y)在一个有限闭区域D上的数值进行求和的方法。

2.计算公式：二重积分的计算可以通过将区域D划分成无限多的小矩形，然后求和每个小矩形内函数f(x,y)的取值，最后对所有小矩形的和取极限来进行计算。

3.表示方法：二重积分可以用符号∬来表示，其中D是区域，f(x,y)是被积函数。

Step 3 二重积分的性质 (20分钟)1. 线性性质：∬[af(x, y) + bg(x, y)]dσ = a∬f(x, y)dσ + b∬g(x, y)dσ，其中a、b为常数。

2.积分区域的可加性:如果D可以分割成两个不相交的区域D1和D2,那么∬f(x,y)dσ=∬f(x,y)dσ1+∬f(x,y)dσ23. 积分次序可交换：若f(x, y)在区域D上连续，那么∬f(x,y)dσ = ∫[c, d]∫[a, b]f(x, y)dxdy = ∫[a, b]∫[c, d]f(x,y)dydx.4.区域的划分不变性：若D1和D2为同一区域D的两个划分方案，则∬f(x,y)dσ1=∬f(x,y)dσ2Step 4 计算二重积分的方法 (30分钟)1. 矩形区域上的二重积分：如果区域D是一个矩形[a, b] × [c,d]，那么∬f(x, y)dσ = ∫[c, d]∫[a, b]f(x, y)dxdy。

2.直角坐标变换：对于区域D在直角坐标下很难表示的情况，可以通过使用适当的直角坐标变换来简化计算。

3.极坐标变换：对于具有对称性或旋转性质的区域D，可以使用极坐标变换来简化计算。

第九章 重积分第一节 二重积分的概念及性质一．二重积分的概念 1．引例引例1 曲顶柱体的体积设有一立体的底是xy 面上的有界闭区域D ，侧面是以D 的边界曲线为准线、母线平行于z 轴的柱面，顶是有二元非负连续函数),(y x f z =所表示的曲面，如图9—1所示，这个立体称为D 上的曲顶柱体，试求该曲顶柱体的体积。

图9—1 图9—2 图9—3解 对于平柱体的体积底面积高⨯=V ，然而，曲顶柱体不是平顶柱体，那么具体作法如下(1)分割把区域D 任意划分成n 个小闭区域nσσσ∆∆∆,,,21Λ，其中iσ∆表示第i 个小闭区域，也表示它的面积。

在每个小闭区域内，以它的边界曲线为准线、母线平行于z 轴的柱面，如图9—2所示。

这些柱面就那原来的曲顶柱体分割成n 个小曲顶柱体。

(2)近似在每一个小闭区域iσ∆上任取一点),(i i ηξ，以),(i i f ηξ为高，iσ∆为底的平顶柱体的体积i i i f σηξ∆),(近似代替第i 个小曲顶柱体的体积。

i i i f V σηξ∆≈∆),((3)求和这n 个小平顶柱体的体积之和即为曲顶柱体体积的近似值∑=∆≈∆=ni i i i f V V 1),(σηξ(4)取极限将区域D 无限细分，且每个小闭区域趋向于或说缩成一点，这个近似值趋近于曲顶柱体的体积。

即∑=→∆=ni i i i f V 10),(lim σηξλ其中λ表示这n 个小闭区域iσ∆直径中最大值的直径（有界闭区域的直径是指区域中任意两点间的距离）。

引例2 平面薄片的质量设有一平面薄片占有xy 面上的有界闭区域D ，它的密度为D 上的连续函数),(y x z ρ=，试求平面薄片的质量。

解 对于均匀平面薄片的质量薄片面积密度⨯=m ，然而，平面薄片并非均匀，那么具体作法如下(1)分割将薄片（即区域D ）任意划分成n 个小薄片nσσσ∆∆∆,,,21Λ，其中iσ∆表示第i 个小小薄片，也表示它的面积，如图9—3所示。

第⼀节⼆重积分的概念与性质第⼀节⼆重积分的概念与性质学习指导１．教学⽬的：使读者理解⼆重积分的概念与性质。

２．基本练习：熟悉⼆重积分的⼏何、物理背景。

熟悉⼆重积分的性质。

3．应注意的事项：⼆重积分是⼆元函数乘积和式的极限，是定积分的推⼴，因此从引例到研究⽅法，从定义到性质都是类似的，读者要善于⽐较，触类旁通，温故⽽知新。

第⼀节⼆重积分的概念与性质⼀、⼆重积分的概念1. 曲顶柱体的体积（1）曲顶柱体（2）曲顶柱体的体积现在我们来讨论如何定义并计算上述曲顶柱体的体积V。

平顶柱体的体积2. 平⾯薄⽚的质量(1) 问题的提出(2) 均匀薄⽚的质量(3) ⾮均匀薄⽚质量的计算⽅法(4) ⼆重积分的定义上⾯两个问题的实际意义虽然不同，但所求量都归结为同⼀形式的和的极限。

在物理、⼒学、⼏何和⼯程技术中，有许多物理量或⼏何量都可以归结为这⼀形式的和的极限。

因此我们要⼀般的研究这种和的极限，并抽象出下述⼆重积分的定义。

定义设是有界闭区域上的有界函数.将闭区域任意分成个⼩闭区域其中表⽰第个⼩闭区域，也表⽰它的⾯积。

再每个上任取⼀点，作乘积，并作和。

如果当个⼩闭区域的直径中最⼤值趋于零时，这和的极限总存在。

则称此极限为函数在闭区域上的⼆重积分，记作，即。

（1）叫做被积函数，叫做被积表达式，叫做⾯积元素，与叫其中积分变量，叫做积分区域，叫做积分和。

(5) 直⾓坐标系中的⾯积元素在⼆重积分的定义中对闭区域的划分是任意的，如果在直⾓坐标系中⽤平⾏于坐标轴的直线⽹来划分，那么除了包含边界点的⼀些⼩闭区域外，其余的⼩闭区域都是矩形闭区域。

设矩形闭区域的边长为和，则。

因此在直⾓坐标系中，有时也把⾯积元素记作。

⽽把⼆重积分记作其中叫做直⾓坐标系中的⾯积元素。

(6) ⼆重积分的存在性这⾥我们要指出，当在闭区域上连续时，式右端的和的极限必定存在，也就是说，函数在上的⼆重积分必定存在。

我们总假定函数在闭区域上连续，所以在上的⼆重积分都是存在的，以后就不在每次加以说明了。

课时：2课时教学目标：1. 理解二重积分的概念及其与定积分的联系。

2. 掌握二重积分的计算方法，包括直角坐标系和极坐标系下的计算。

3. 能够运用二重积分解决实际问题。

教学重点：1. 二重积分的概念和性质。

2. 二重积分的计算方法。

教学难点：1. 二重积分的实际应用。

2. 在不同坐标系下进行二重积分计算。

教学准备：1. 多媒体课件。

2. 练习题。

3. 黑板或白板。

教学过程：第一课时一、导入1. 复习定积分的概念，引出二重积分的概念。

2. 提问：什么是定积分？定积分在几何和物理上有什么应用？二、新课讲解1. 二重积分的定义：- 利用二重积分的定义，讲解在直角坐标系和极坐标系下的二重积分。

- 举例说明如何将二重积分转化为两次定积分。

2. 二重积分的性质：- 讲解二重积分的基本性质，如线性性质、保号性质、可积性等。

- 通过实例说明这些性质的应用。

三、例题讲解1. 直角坐标系下的二重积分计算：- 举例说明如何计算直角坐标系下的二重积分。

- 讲解计算过程中的注意事项。

2. 极坐标系下的二重积分计算：- 举例说明如何计算极坐标系下的二重积分。

- 强调极坐标系在计算二重积分时的优势。

四、课堂练习1. 学生独立完成课堂练习，巩固所学知识。

2. 教师巡视指导，解答学生疑问。

第二课时一、复习1. 复习上一节课所学内容，重点强调二重积分的定义、性质和计算方法。

二、新课讲解1. 二重积分的实际应用：- 举例说明二重积分在几何、物理和工程中的应用。

- 讲解如何将实际问题转化为二重积分问题。

2. 不同坐标系下的二重积分计算：- 举例说明在不同坐标系下进行二重积分计算的技巧。

三、例题讲解1. 复习直角坐标系和极坐标系下的二重积分计算例题。

2. 讲解如何根据实际问题选择合适的坐标系进行计算。

四、课堂练习1. 学生独立完成课堂练习，巩固所学知识。

2. 教师巡视指导，解答学生疑问。

五、总结1. 总结二重积分的概念、性质和计算方法。

2. 强调二重积分在实际应用中的重要性。

二重积分的概念与性质教案一、教学目标1. 理解二重积分的概念，掌握二重积分的几何意义。

2. 掌握二重积分的性质，包括对称性、周期性和线性性质。

3. 学会计算简单的二重积分，并能应用于实际问题。

二、教学重点与难点1. 二重积分的概念与几何意义。

2. 二重积分的性质及其应用。

三、教学方法1. 采用讲授法，讲解二重积分的概念、性质及计算方法。

2. 利用图形和实例，帮助学生直观地理解二重积分的几何意义。

3. 引导学生通过小组讨论和思考，发现二重积分的性质。

四、教学准备1. 教学PPT。

2. 相关图形和实例。

3. 练习题。

五、教学过程1. 引入：回顾一重积分的概念和性质，引导学生思考二重积分的可能性。

2. 讲解二重积分的概念：通过图形和实例，引导学生理解二重积分的几何意义。

3. 讲解二重积分的性质：（1）对称性：以对称区域为例，说明二重积分在对称区域上的特点。

（2）周期性：以周期函数为例，说明二重积分在周期区域上的特点。

（3）线性性质：结合线性代数知识，讲解二重积分的线性性质。

4. 例题讲解：选取典型的二重积分题目，讲解计算方法和应用。

5. 课堂练习：让学生独立完成练习题，巩固所学知识。

7. 作业布置：布置相关练习题，巩固所学知识。

六、教学拓展1. 引入高维空间中的二重积分：讲解在更高维空间中的二重积分概念和性质，引导学生理解多变量函数的积分。

2. 讲解二重积分的计算方法：（1）极坐标变换：讲解如何利用极坐标变换计算二重积分。

（2）柱坐标变换：讲解如何利用柱坐标变换计算二重积分。

（3）球坐标变换：讲解如何利用球坐标变换计算二重积分。

七、实践与应用1. 利用二重积分解决实际问题：举例讲解如何将实际问题转化为二重积分问题，并求解。

2. 利用二重积分求解物理问题：讲解如何利用二重积分求解物理中的场强、热量等问题。

八、课堂讨论与思考1. 组织学生进行小组讨论：让学生探讨二重积分在实际应用中的局限性和改进方法。

2. 引导学生思考：鼓励学生思考二重积分在多变量函数分析中的应用，以及如何拓展二重积分的性质。

二重积分的教案教案名称：二重积分的教学设计教学目标：1.了解二重积分的概念和基本性质；2.掌握二重积分的计算方法和应用；3.培养学生的数学思维和问题解决能力。

教学准备：1.教师准备教学课件和教学实例；2.学生需要具备微积分基础知识。

教学过程：一、导入（5分钟）1.教师可以通过引入实际问题，让学生思考如何计算某个区域的面积或者质量等问题，引出二重积分的概念；2.提问：如何计算某个区域的面积？如何计算某个平面薄片的质量？3.引导学生思考，引出二重积分的概念。

二、概念讲解（15分钟）1.教师通过演示或者动态图像，讲解二重积分的概念和几何意义；2.解释二重积分的定义：将被积函数在所给曲边梯形上的积分作为极限形式加以定义。

三、性质讲解（15分钟）1.教师讲解二重积分的可加性、线性性、保号性等基本性质；2.指出二重积分与偏导数的关系，引导学生思考。

四、计算方法（20分钟）1.教师分别讲解二重积分的直角坐标和极坐标下的计算方法；2.通过教学实例，演示如何计算不规则区域的面积和质量。

五、应用举例（20分钟）1.教师提供实际问题，引导学生应用二重积分求解；2.根据教师给出的问题，学生利用二重积分的概念和计算方法，进行解答。

六、拓展与归纳（10分钟）1.教师要求学生总结二重积分的基本概念、性质和计算方法；2.学生再次回顾课程内容，提出疑问和问题。

七、提问与讨论（10分钟）1.教师提问学生关于二重积分的问题；2.学生提出疑问和思考，讨论与交流。

八、课堂练习（15分钟）1.教师出示练习题，让学生在课堂上进行解答；2.教师引导学生思考解题方法和思路。

九、作业布置（5分钟）1.教师布置课后作业，巩固学生对二重积分的理解和应用；2.教师提醒学生按时完成作业，并预告下一节课的内容。

教学反思：本节课通过概念讲解、性质讲解、计算方法、应用举例和拓展归纳等教学环节，全面系统地介绍了二重积分的概念和基本性质，培养了学生的数学思维和问题解决能力。

第九章重积分第一节二重积分的概念及性质重积分的概念1 •引例引例1曲顶柱体的体积设有一立体的底是xy面上的有界闭区域D，侧面是以D的边界曲线为准线、母线平行于z轴的柱面，顶是有二元非负连续函数z f(x,y)所表示的曲面，如图9—1所示, 这个立体称为D上的曲顶柱体，试求该曲顶柱体的体积。

图9—1 图9—2 图9 —3解对于平柱体的体积V高底面积，然而，曲顶柱体不是平顶柱体，那么具体作法如下(1)分割把区域D任意划分成n个小闭区域，，，，其中表示第i个小闭区域，1 2 n i也表示它的面积。

在每个小闭区域内，以它的边界曲线为准线、母线平行于z轴的柱面，如图9—2所示。

这些柱面就那原来的曲顶柱体分割成n个小曲顶柱体。

⑵近似在每一个小闭区域上任取一点(，)，以f ( i , i)为高，为底的平顶柱体i I / i的体积f( i, i) i近似代替第i个小曲顶柱体的体积V f ( i, i)(3) 求和这n 个小平顶柱体的体积之和即为曲顶柱体体积的近似值nV V f ( i, i) ii1(4) 取极限将区域D无限细分，且每个小闭区域趋向于或说缩成一点，这个近似值趋近于曲顶柱体的体积。

即nV lim0 f ( i, i ) ii1其中表示这n 个小闭区域直径中最大值的直径(有界闭区域的直径是指区i 域中任意两点间的距离) 。

引例2 平面薄片的质量设有一平面薄片占有 xy面上的有界闭区域D，它的密度为D上的连续函数z (x, y) ，试求平面薄片的质量。

解对于均匀平面薄片的质量m 密度薄片面积，然而，平面薄片并非均匀，那么具体作法如下(1)分割将薄片(即区域D )任意划分成n个小薄片，其中表示第i个1 2 n i小小薄片，也表示它的面积，如图9—3 所示。

(2)近似在每一个小薄片」上任取一点(「丿，以(i, J为其密度，当i很小时，认为小薄片是均匀的，则(i, i) i近似代替第i个小薄片的质量。

即m ( i , i) i(3)求和这n个小薄片的质量之和即为薄片的质量的近似值i1(4) 取极限将薄片D 无限细分，且每个小薄片趋向于或说缩成一点， 这个近似值趋近于薄片 的质量。

7.1二重积分的基本概念（教案）主讲人：孙杰华教学目的：理解二重积分的概念、性质教学重难点：二重积分的概念、二重积分的几何意义. 教学方法：讲授为主 教学内容：一、二重积分的概念 1．曲顶柱体的体积设有一空间立体Ω,它的底是xoy 面上的有界区域D ,它的侧面是以D 的边界曲线为准线,而母线平行于z 轴的柱面,它的顶是曲面(.)z f x y =，称这种立体为曲顶柱体.与求曲边梯形的面积的方法类似，我们可以这样来求曲顶柱体的体积V : (1)用任意一组曲线网将区域D 分成n 个小区域1σ∆，2σ∆，，n σ∆，以这些小区域的边界曲线为准线,作母线平行于z 轴的柱面,这些柱面将原来的曲顶柱体Ω分划成n 个小曲顶柱体1∆Ω，2∆Ω，，n ∆Ω.（假设i σ∆所对应的小曲顶柱体为i ∆Ω,这里i σ∆既代表第i 个小区域,又表示它的面积值,i ∆Ω既代表第i 个小曲顶柱体,又代表它的体积值.)，从而1ni i V ==∆Ω∑．图7.1(2)由于(,)f x y 连续,对于同一个小区域来说,函数值的变化不大．因此,可以将小曲顶柱体近似地看作小平顶柱体,于是(,),((,))i i i i i i i f ξησξησ∆Ω≈∆∀∈∆.(3)整个曲顶柱体的体积近似值为1(,)ni i i i V f ξησ=≈∆∑.(4)为得到的精确值,只需让这个小区域越来越小,即让每个小区域向某点收缩．为此,我们引入区域直径的概念:一个闭区域的直径是指区域上任意两点距离的最大者. 所谓让区域向一点收缩性地变小,意指让区域的直径趋向于零. 设n 个小区域直径中的最大者为λ,则1lim (,),(,)ni i i i i i i V f λξησξησ→==∆∀∈∆∑.2．二重积分的定义设(),f x y 是闭区域D 上的有界函数, 将区域D 分成个小区域12,,,,n σσσ∆∆∆其中,i σ∆既表示第i 个小区域,也表示它的面积, i λ表示它的直径.1max{}(,)i i i i i nλλξησ≤≤=∀∈∆，作乘积(,)(1,2,)i i if i n ξησ∆=，作和式1(,)niiii f ξησ=∆∑，若极限()01lim,niiii f λξησ→=∆∑存在,则称此极限值为函数(),f x y 在区域D 上的二重积分,记作(),Df x y d σ⎰⎰.即(),Df x y d σ=⎰⎰()01lim ,ni ii i f λξησ→=∆∑．其中:(),f x y 称之为被积函数,(),f x y d σ称之为被积表达式,d σ称之为面积元素,,x y 称之为积分变量,D 称之为积分区域.V n3．对二重积分定义的说明：(1)极限()01lim,niiii f λξησ→=∆∑的存在与区域D 的划分及点(,)i i ξη的选取无关。

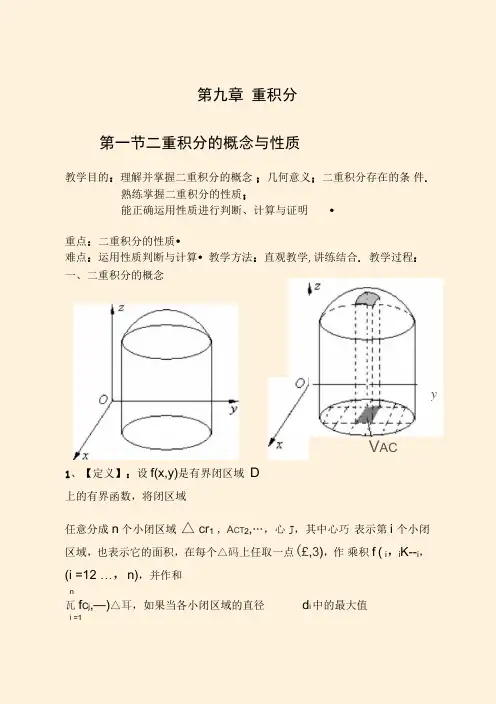
V AC：第九章 重积分第一节二重积分的概念与性质教学目的：理解并掌握二重积分的概念 ；几何意义；二重积分存在的条 件.熟练掌握二重积分的性质；能正确运用性质进行判断、计算与证明•重点：二重积分的性质•难点：运用性质判断与计算• 教学方法：直观教学,讲练结合. 教学过程： 一、二重积分的概念1、【定义】：设f(x,y)是有界闭区域 D 上的有界函数，将闭区域任意分成n 个小闭区域 △ cr 1 , A CT 2,…，心J ，其中心巧 表示第i 个小闭区域，也表示它的面积，在每个△码上任取一点(£,3)，作 乘积 f ( i ，i K--i ，(i =12 …，n)，并作和n瓦f c j ,—)△耳，如果当各小闭区域的直径d i 中的最大值i =1yn■二max{d}r 0时，这和式lim f( 1, 的极限存在，且1_11> 0 v此极限与小区间人码的分法以及点(©,3)的取法无关，则称此极限为函数f (x, y)在闭区域D上的二重积分，记为I l f (x, y)d匚，即DnH f (x,y)db =|再送f(©,0)^w.其中：① f (x, y)称为被积函数，②f(x, y)d二称为被积表达式③x, y称为积分变量，④d二称为面积元素，⑤ D称为积分区域⑥' f ( i , i) *i称为积分和.i 12、面积元素de在直角坐标系下用平行于坐标轴的直线网来划分区域D,则面积元素为d；「= dxdy故二重积分可写为11 f (x, y)d3、【二重积分存在定理】设f (x, y)是有界闭区域D上的连续函数，则存在二重积分j\| f (x, yjdb .D4、二重积分的几何意义(1)当被积函数f ( x, y)_ 0寸,二重积分f(x, y)d二表示以Df (x,y)为顶，以D为底面的曲顶柱体的体积.⑵当被积函数f(x, y)乞0时,二重积分表示曲顶柱体体积的相反数.二、二重积分的性质假设被积函数在有界闭区域D上连续•D1. !!kf (x, y)d；「十!! f (x, y)d二,k为常数.2. .[f(x,y)_g(x,y)]d；「- f (x,y)d；「一g(x, y)d；「•D D D设：•，：为常数则上述两式合并为M[: f(x,y) ：g(x, y)]d；「「f(x, y)d一亠)i ig(x, y)d二.D D D3.(二重积分对区域可加性)f(x,y)d；「= f(x, y)d；「f(x, y)d二，(D 二D“ D? ) •D D1 D 24.. d；「- 丁，匚为D的面积.D5.(积分不等式)若f (x, y) 一g (x, y)，则!! f (x, y)d；「一g(x, y)d二.D D推论:口f (x, y)d仃 M 皿f (x, y)|d<T .D D6.(积分估值定理)设M、m分别是f (x,y)在闭区域D上的最大值和最小值，贝U m；「一f(x, y)d=_M二.D7.(积分中值定理)设函数f (x,y)在闭区域D上连续，则在D上至少存在一点「，)使得 - f( x, y)d二f(,.)CJ 丁&设区域D = D! D2，且u与D2关于x轴对称；(1)当f (x, y)关于y是偶函数时即f(x, —y)= f (x, y)时，有f(x,y)^ =2 f (x, y)d二•D D i⑵当f (x, y)关于y是奇函数时即f (x, —y)= - f (x, y)时，有Mf(x,y)d匚=0.D类似有设区域D, D2，且D,与D2关于y轴对称；当f(x,y)关于x是偶函数时即f(-x,y)= f(x,y)时，有f (x, y)d；「- 2 f(x, y)d二.D D i⑵当f (x, y)关于x是奇函数时即f(-x, y)= -f (x, y)时，有解：如图，由于点A(1,0)在(x-2)2• (y 一1)2乞2上，过点A的切线为x+y=1,那么在D 上有1 兰x + y 兰(x + y)2W (x + y)3,所以H(x +y)2db v JJ(x +y)3dc<D D例2(05.4)设| j = fjcosjx2十y2db , l2= JJcos(x2+ y2)d口,D D2 2 2 2 2l3= ffcos(x + y ) d G ,其中D ={( x, y) | x + y ^1},则D(A) I3 >丨2 >丨1 (B) I1 > 丨2 > 13(C)丨2 > 丨1 >丨3 (D) I3 >丨22 2 二答(A).因为在区域D上，0兰x2+y兰1成一，2所以—>1 兰J x2+ y2M x2+ y2兰(x2+ y2)2M 0 ,2从而cos(\ x2十y2)兰cos(x2十y2)兰cos(x2+ y2)2.例3设D : x2+ y2兰a2,当a =()时，口Ja2_x2 _ y2dxdy =兀.D(a) 1答(b).根据二重积分的几何意义，此积分表示半径为a的上半球体1 4 3 3的体积•由一一=兀得a =3/一二选(b).2 3 、、2例4当D是由( )围成的区域时，…dxdy = 1.D(讣冷，(d) x + y =1，x - y = 1(a) x 轴，y 轴及2x y-2=0 ( b)x=1,x=2 及y=3,y=4答(a，b，c).因为dxdy二1表示积分区域的面积为1，故只需考察哪D些选项积分区域的面积为1.即可=选(a)，( b)，( c).例5判断..In (x2• y2)d；「的正负•|x|「y| 丄解：在区域D ={(x，y) ||x| +|y| <1}上有x2 +y2兰1且等号不恒成立，2 2所以ln(x y )汨n1 =0且等号不恒成立，故JJ In(x2+y2)d^ v JJ (In 1)d^=0.x| ;y|」x；y|」例6估计积分值I = xy(x y)d二，D 二{(x，y) | 0 乞x 乞1,0 乞y 乞2}.解：0 -xy(x2 y2) - 6= 0-1 -12 .例7 D1 珂(x, y)|x y "x,y -0}, D? ={( x, y)|(x—2)2 (y—1)2 "}.h =〕J(x+y)2d<r,l2 = ”(x + y)3ds I3 = j](x + y)2d&D1 D1 D 21厂(x・y)3d匚用适当符号连接l1,l2, l3,l4.D2解：在D i 上有l i • l2(0 —x y —1),在D2上I4 l3(x y_1).2 1又由(x + y)兰1二—，由2D1(x +y)231 二l3JJ d b =2兀>^ > l1,2D2故l4 l311 l2.例8 设D ={( x,y) |1 岂x2y2乞4}，证明3二e e"『d；：「- 3：e4.D证明S D Y - 4二-二-3二，e岂e x2“ < e4，由积分的估值性质得2 23「e _ e x y d；「_3二e .D例9 设D ={( x,y)|x2 y2乞R2}(1)若f(x,y)在D上有界且可积，则l』m(11 f (x, y)d；「=0.D1(2)若f (x,y)在D 上连续，则I』叫二f (x, y)d；「-二f(0,0) •R T R D(1)证明：设m, M分别为函数f (x, y)在D上的最小值与最大值，则m< f (x, ypiM，由积分估值定理知..md；：•一- f(x,y)d；丁- Md匚D D D又D ={( x, y) |x2y2 - R2}所以二mR2— f (x,y)d；「- ：MR2，D由夹逼定理得R m。