§1电流的稳恒条件
- 格式:ppt
- 大小:968.50 KB
- 文档页数:24

第三章稳恒电流(Steady Current)[基本要求]1、理解电流密度概念及其与电流强度的关系。
2、理解稳恒电流及稳恒电场的意义和它们的基本性质。
3、掌握电动势的概念。
4、掌握欧姆定律的微分形式,学会用场的观点去阐述电路的原理。
5、理解基尔霍夫方程组,学会用基尔霍夫定律解题。
6、了解温差电现象、电子发射与气体导电。
[重点难点]1、理解稳恒电场的概念及与静电场的异同,明确稳恒电流的条件,理解其数学表达式的物理意义。
2、电流密度矢量和电动势是本章的两个基本概念,要着重理解它们的物理意义。
3、欧姆定律的微分形式(不含源电路,含源电路),学会用场的观点去阐述电路的原理。
[教学内容]§1 电流的稳恒条件和导电规律一.电流强度,电流密度矢量1.电流·电流—带电粒子的定向运动。
·载流子—形成电流的带电粒子。
例:电子、质子、离子、空穴。
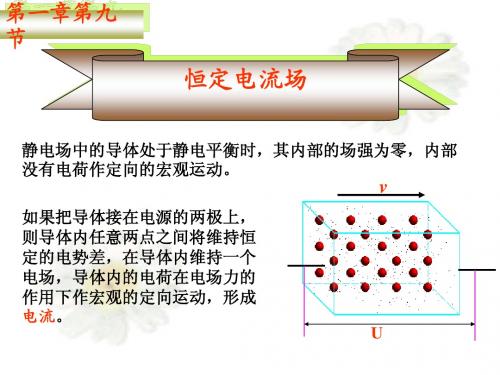
·电流形成条件(导体内):(1)导体内有可以自由运动的电荷;(2)导体内要维持一个电场。
(导体内有电荷运动说明导体内肯定有电场,这和静电平衡时导体内场强为零情况不同。
) 2.电流强度·大小:单位时间内通过导体某一横截面的电量。
·方向:正电荷运动的方向 ·单位:安培(A )3.电流密度(Current density) ·电流强度对电流的描述比较粗糙:况。
·引入电流密度矢量—描写空间各点电流大小和方向的物理量。
·某点的电流密度:是一个矢量。
方向:该点正电荷定向运动的方向。
大小:通过垂直于该点正电荷运动方向的单位面积上的电流强度。
单位:安培/米 2·电流场:导体内每一点都有自己的j, ),,(z y x j jdtdqt q IlimdS dI j即导体内存在一个j场---称电流场。
·电流线:类似电力线,在电流场中可画电流线。
3.电流密度和电流强度的关系 (1)通过面元d S 的电流强度d I = j d S = j d S cos(2)通过电流场中任一面积S 的电流强度s d j I电流强度是通过某一面积的电流密度的通量。


第三章 稳恒电流前几章(真空、导体与电介质)为静电学,涉及静止电荷的电现象;本章论述有关运动电荷知识。
带电粒子运动伴有电量迁移而形成电流,若电流不随t 而改变,则称为稳恒电流,即直流(DC)。
研究方法:路论,重点以金属导体为例研究规律及计算。
§1 稳恒电流的闭合性及导电规律一、电流电荷的定向移动形成电流。
1、产生电流的条件产生电流需要两方面的条件:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧.;);(.;);(,机械作用等化学作用本章以此为主电场作用的某种作用有迫使电荷作定向运动对半导体中:电子、空穴离子、电子流电解液、气体中:正负本章以此为主金属中:自由电子即载流子荷存在可以自由移动的电 2、电流方向惯例规定:正电荷流动的方向。
多数情况下导电由负电荷引起,而正电荷沿某方向定向运动与负电荷沿反方向运动产生相同效果(注:有例外,如霍耳效应)。
二、电流强度和电流密度矢量1、电流强度I金属中自由电子作无规则热运动,即使在K T 0=,仍s m u 610≈热,但0=热u 。
故无宏观净电量迁移。
定向运动形成宏观净电荷迁移,此定向运动为漂移运动v需由电场提供力作用来完成,漂v 虽小,约为104-sm 量级,但却形成宏观电流。
电流强弱用电流强度I 描述,定义如下:dtdq I =即导体中单位时间通过的某一给定截面的电量为通过该面的电流强度。
(不涉及导体截面粗细和截面上电流详细分布)。
[说明](1) I 为标量,单位为:安培(A )—— SI 制中基本单位之一。
秒库安11=, A mA A μ6310101==(2) 仅粗略描述单位时间内通过某一曲面(可大可小、可任意形状)的总电量,不够点点详细,如图4-1所示。
(a) I 相同,但分布有别 (b) 高频趋肤(c) 电阻法探矿 (d) 用电流场模拟静电场图4-1下面引入电流密度矢量J详细描述电流场分布。
2、电流密度矢量J),,(z y x J J=是空间坐标的矢函数,其定义为:⎪⎪⎩⎪⎪⎨⎧⋅=⊥,即电流方向。


第三章稳恒电流第三章稳恒电流§1 电流的稳恒条件和导电规律§2 电源与电动势§3 基尔霍夫定律1§1 电流的稳恒条件和导电规律电荷的定向运动形成电流。
传导电流的产生条件:存在可移动电荷(自由电荷)存在电场,即ΔU≠0,或E≠0 ,或某种非静电力注:超导体除外2一. 电流强度 I1. 电流强度:MKSA基本量之一大小:I =Δq/Δt 或 I = dq/dt 方向:正电荷运动方向(电场方向); 单位:A2. 稳恒电流:I 不随时间变化必要条件:导体中任意两点间电势差ΔU=const , r 或导体中任意一点处的场强 E = 恒矢量.3. 稳恒电流的连续性电流管:I入= I出反证法:若 I入≠ I出,必有电荷堆积, r 则导致 E 变化,破坏稳恒条件. n 个支路:∑ I 入= ∑ I 出, ∑ I k = 0k =1 n电流管3r 二. 电流密度矢量 j1.r dI r n 定义:j = dS ⊥ 单位垂直面积通过的电流强度 ? 大小:r ? ? 方向: n 电流的方向r r dI = jdS ⊥= j cos θdS = j ? dS电流强度是电流密度的通量:I = ∫∫r r 2. 电流连续方程:j ? dS = ? d q ∫∫ dt S(电荷守恒)Sr r j ? dSr ?ρ ?? j + =0 ?t4r r 3. 电流稳恒条件:∫∫ j ? dS = 0Sr ?? j = 0三. 欧姆定律r r 稳恒电场与静电场相似,有∫ E ? d l = 0L1. 欧姆定律U I= R1 G I = GU, = R——可引入“电压”R ——电阻(欧姆) G ——电导(西门子)或2. 电阻率1 1 l 或σ =ρ , R=σ S 一般ρ = ρ 0 (1 + α t )l R =ρ Sρ ——电阻率(欧姆· 米)西门子σ ——电导率(米)α ——电阻温度系数53. 欧姆定律的微分形式ΔSΔU ΔI Δl 一段小电流管沿电流管取一小圆柱体,长Δl,截面ΔS,电势差ΔU,电流ΔI . 由欧姆定律: 故取极限,得1 ?l ?U ?I = , R= R σ ?SU ?I ?U ?I = σ ?S , 或=σ ?l ?l ?Sj = σE r r j = σE ——欧姆定律的微分形式64. 金属导电的经典解释——电流形成与电阻机理导体中无电场(亦无电子数密度梯度、温度梯度或其它可使电子宏观运动的因素), 穿过任一截面的电流为零. 电子作热运动,电子与原子核碰撞、散射,其路径是曲折的。
恒定电流的条件
1. 恒定电流的条件之一就是得有个持续的动力源呀!就像汽车要跑起来得有发动机持续提供动力一样,要是没有这个,那电流还怎么恒定呀!
2. 电路还得是通畅的呢,这就好比道路不能有堵塞呀!如果到处都是断路,那电流还能顺畅地流吗?
3. 电阻也得稳定呀,你想想,要是电阻一会儿大一会儿小,那电流不就跟坐过山车似的,能恒定吗?就像你跑步的速度,总不能一会儿快一会儿慢还说自己是匀速跑吧!
4. 电源的电动势也得稳稳的呀,这就像人的心脏得有力地跳动一样,要是电动势不稳定,那电流能恒定吗?
5. 恒定电流还需要各个部分协调配合呀!这不就跟一个团队一样,大家都得好好合作,不然怎么能成功呢?
6. 还得有合适的导体呀,不然电流怎么能好好地通过呢?就像人得走在合适的道路上才能顺利到达目的地呀!
7. 没有外界的干扰也很重要哦!你想想,要是总有人在旁边捣乱,你能安心做事吗?电流也是一样呀!
8. 恒定电流得有个稳定的环境呀,就像你学习得有个安静的环境一样,总不能周围乱糟糟的还能学好吧?
9. 各元件的性能也得可靠呀,要是动不动就出问题,那电流还怎么恒定呢?这跟你交朋友一样,可靠的朋友才让人放心嘛!
10. 最后呀,所有这些条件都得同时满足,少一个都不行呢!就像搭积木,缺一块都搭不起来呀!
我的观点结论:要实现恒定电流,这些条件真的一个都不能少,都很关键呀!。