对称性分岔理论基础(唐云著)思维导图

图形推理第一节平面规律推理概述题目特征：题干给出若干个图形，要求考生通过观察找出图形之间排列的规律，选出符合规律的一项。

解题思维：（1）观察给出图形构成的特点；（2）根据特点总结图形间的规律；（3）根据规律结合选项推出答案。

确定图形构成的特点是解答图形推理的起点，具体如下：（1）图形组成元素相同，一般考查位置规律；（2）图形组成元素相似，一般考查样式规律；（3）图形组成元素不同，一般考查属性、数量及其他特殊规律。

第二节位置规律位置规律是图形推理的一个高频命题规律。

题型特征：图形元素组成完全相同常考的位置规律有三种：平移、旋转、翻转考点一：平移平移是指图形中的某一个或几个元素沿特定方向进行规律移动。

常见考法：（1）平移方向。

①直线方向：上下平移、左右平移②时针方向：顺时针平移、逆时针平移（2）平移的步长（移动几格）：恒定、递增（递减）提示：遇到平移问题，一般先判断平移的方向（怎么走），后判断平移的步长（走几步）。

考点二：旋转旋转是指图形在平面上按特定规律进行转动。

常见考法：（1）旋转的方向（怎么转）：顺时针旋转、逆时针旋转。

（2）旋转的角度（转几度）：恒定、规律变化。

考点三：翻转翻转是指图形仅痛殴平面转动无法变化得到，必须经过类似于"翻书"的动作才能得到。

常见考法：（1）翻转的方向（怎么翻）：关于横轴（x轴）进行上下翻转，或关于纵轴（y轴）进行左右翻转，或关于自身对称轴进行自身对折。

（2）翻转和旋转的区分：利用"时针法"进行判断。

第三节样式规律样式规律是图形推理的一个高频命题规律。

题型特征：图形元素组成相似，优先考虑样式规律。

常见考点：样式遍历、加减同异、黑白运算考点一：样式遍历通俗地说，遍历就是缺什么补什么，首先要求构成图形的元素在一定范围内都要出现，在此基础上要求元素出现的次数相同。

常见考法：（1）整体遍历（2）部分遍历考点二：加减同异加减同异是指两个图形经过相互加、减、去异存同、去同存异得到一个新图形。

第二节 对称性和布拉维格子的分类
本节主要内容: 一、群的知识简介 二、点群和七个晶系 三、空间群和14种布拉维格子 四、点群对称性和晶体的物理性质
§2.2 对称性和布拉维格子的分类
布拉维格子是按其对称性(symmetry)来分类的：
所谓对称性是指在一定的几何操作下，物体 保持不变的特性。
对称性在物理学中是一个非常重要的概念， 它可使复杂物理现象的描述变得简单、明了。 因为对称性的本质是指系统中的一些要素是等 价的。对称性越高的系统，需要独立表征的系 统要素就越少，因而描述起来就越简单。
a31 a32 a33 0 0 1
A 1
还有：以z=0作为镜面，则有：
x x
y
y
z z
a11 a12 a13 1 0 0 Aa21 a22 a230 1 0
a31 a32 a33 0 0 1
A 1
由上可以看出，当变换是纯转动时，矩阵的行 列式等于+1；当是空间反演或镜面反射时等于1.前一种对应物体的实际运动，另一种不能靠物 体的实际运动来实现。
O
四个3次轴、三个4次轴，按八面体型分布
熊 为了表明对称面相对于旋转轴的位置，还有如下附加指标： 夫 下角标h(水平)表示垂直于旋转轴 利 符 下角标v(铅直)表示平行于旋转轴 号
下角标d(对角)表示平行于主轴且平分2次轴之间的夹角
国际符号
国际符号以不超过三个几何上的从优方向 来描述晶体的对称类型，这些方向或平行于对 称轴或垂直于对称面
我们这里要讨论的主要是晶格(或点阵)的对 称性(symmetry of lattice).
在晶格这个物理系统中，一种对称性是指某些 要素互相等价，而用来描述晶格的要素，无非就 是：点、线、面。而保持这些要素等价的操作---对称操作有三种：平移、旋转、镜反射。假设 在某一个操作过后，点阵保持不变，也就是每个 格点的位置都得到重复，那么这个相应的平移、 旋转或镜反射操作就叫作一个点阵对称操作。其 中的点、线、面分别叫做对称中心、对称轴、对 称面----称为对称元素

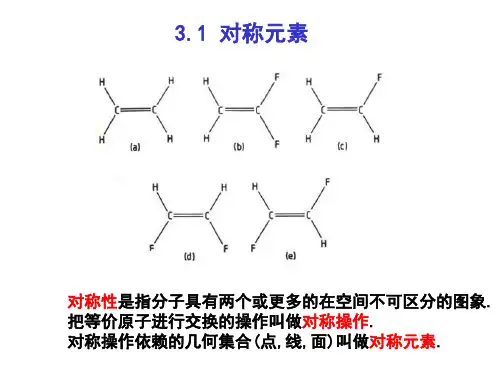
第三章分子的对称性3.1 对称操作与对称元素3.2分子点群3.3 分子的对称性和分子的物理性质对称在自然界中普遍存在。

北京天坛北京地坛在化学中，我们研究的分子、晶体等也有各种对称性。

有时会感觉这个分子对称性比那个分子高（如HF、H2O、NH3、CH4 、PF5 、SF6）。

如何表达、衡量各种对称？数学中定义了对称元素来描述这些对称。

3.1 对称操作与对称元素•对称操作：是指不改变物体内部任何两点间的距离而使物体复原或与原分子等价的操作。

•对称元素：对称操作所依据的几何元素。

•对称元素与对称操作紧密联系又有区别。

•点操作：对于分子等有限物体，在进行操作时，物体中至少有一点是不动的，这种对称操作叫点操作。

点对称操作和相应的点对称元素旋转反映操作旋映轴S n反演操作对称中心I 反映操作对称面σ旋转操作对称轴（真轴）C n 恒等操作恒等元素E对称操作对称元素符号分子中若存在一条轴线，绕此轴旋转一定角度能使分子复原或与原分子等价，就称此轴为旋转轴，符号为C n 。

1. 对称轴C n和旋转操作旋转轴的性质C n 旋转轴能生成n 个旋转操作，记为：EC C C C C C n n n n n n n n ˆˆ,ˆ,,ˆ,ˆ,ˆˆ1321=⋅⋅⋅=−m n m n b a nb n a n C C C C C ˆˆˆˆˆ22==⋅+•基转角：和C n 轴相应的基本旋转操作为Ĉn 1，它为绕轴转360˚/n 的操作，该旋转角度为基转角。

旋转角度按逆时针方向计算。

C n 旋转轴有如下性质：分子中若有多个旋转轴，轴次最高的轴一般叫主轴，其它的叫副轴。

通常将主轴取笛卡尔坐标的z轴。

旋转可以实际进行，旋转轴称为真轴。

分子中若存在一个平面，将分子两半部分互相反映而能使分子与原分子等价，则该平面就是对称面σ（镜面），这种操作就是反映。

=为奇数）（为偶数）n n E nσσˆ(ˆˆ2.对称面σ和反映操作和主轴垂直的镜面以σh 表示；通过主轴的镜面以σv 表示；通过主轴，平分副轴夹角的镜面以σd 表示。

s ˆxz x ,y ,z x ,y ,z C ˆ4,zx,y ,z y ,x,z
y
p
s s ˆ x C ˆ z 4 ,z x ,y ,z ˆ x y z ,x ,z y ,x ,z
x
s s ˆ x C ˆ z 4 ,z x ,y ,z ˆ x y z ,x ,z y ,x ,z
记为 Cˆ n ；相应地，旋转轴也称为真轴，记为 Cn 。
H2O2 中的 C2
能使图形复原所必须转动的最小角度（ 0o 除外 ），称
为基转角 a 。
对称轴的轴次： n 360 α
一个 n 重对称轴包含 n 个对称操作，可表示为：
C n (C ˆn 1 ,C ˆn 2 , ,C ˆn i, ,C ˆn n E )
4.1 生活中的对称性
生 物 界 的 对 称 性
立方 ZnS 型晶体模型 NaCl 型晶体模型
B6H6
B5H9
4.2 对称操作与对称元素
我们在谈论生活中的对称性时，更多的是定性的，和 出于美感的。然而，当我们开始讨论分子的对称性时，必 须对分子对称性的含义具有明确的概念。
使对称概念严格、系统化，是从引进，并明确“对称 操作”的基本概念开始的。
但这些特殊的例子能够帮助我们理解对称元素的组合原如果存在n次旋转轴c垂直的二次旋转轴c轴与轴的组合bf432对称元素组合原理22n的二个二次旋转轴c决定的平面的垂直方向上过交点有一个n次旋转一个具体的例子是我们刚刚证明了
第四章 分子对称性
目录
4.1 生活中的对称性 4.2 对称操作与对称元素 4.3 对称元素组合原理 4.4 对称性与分子的偶极矩、旋光性 4.5 分子点群
可以证明，分子或有限图形所具有的所有可能的对称类 型只有 5 种：E，Cn，s，i，Sn(In) 。

如果一个操作产生的结果和两个或多个其它操作连续作用的结果 相同，通常称这一操作为其它操作的乘积。
若 A ˆB ˆC ˆ，则 C ˆ为 称 A ˆB ˆ的乘积。 若A ˆBˆ BˆA ˆ， 则A ˆ和 称Bˆ是 可 交 换 的 。
例如H2O的对称操作。
21
E,C2,v(x)z,v(y)z E ˆC ˆ2C ˆ2E ˆC ˆ2
对应的两个原子和中心点同在一条直线上，且到中心点的距离相
iˆ 等，这一点就是对称中心i,这种操作就是反演
.
反式二氯二溴乙烷
14
H
H
Cl H
CC
Cl
HH
H Cl
Cl Pt Cl
H
Cl
FF B
O
HH F
H
iˆ2n ˆ
iˆ2n1 iˆ
15
(5)象转轴Sn与旋转反映操Sˆ作n Sˆ n
如果图形绕轴旋转一定角度后，再作垂直此轴的镜面反映， 可以产生分子的等价图形。则将该轴和镜面组合所得到的对称 元素称为象转轴。
映 .ˆ
11
按和主轴的关系对称面可分为： V面：包含主轴； h面：垂直于主轴； d面：包含主轴，且平分两个相邻的C2轴的夹角。
12
PtCl4
ˆ2n Eˆ
ˆ2n1 ˆ
13
(4) 对称中心i与反演操作 iˆ
分子中若存在一个中心点,对于分子中任何一个原子来说，
在中心点的另一侧，必能找到一个和它相对应的同类原子，互相
4
C
1 4
3
4 3
1
4
2
2 1
h
2 1
4 3
18
Sˆ nk
ˆ h
Cˆ
k n

反式二氟乙烯
C2垂直于荧光屏, σh 在荧光屏上
若n为偶数,Cn轴也是C2轴,属于Cnh的分子有对称中心
C3h 群
R
R
C3垂直于荧光屏, σh 在荧光屏上
R
Cnv群：分子有一个Cn轴和n个竖直的对称面（通过Cn轴）
H2O中的C2和两个σv
C3v ：NF3
有一个Cn轴和n个C2的群:包括Dn、Dnh、Dnd
(2) 甲烷具有S4，且只有 C2与S4共轴，但C4和与之垂 直的σ并不独立存在.
CH4中的映轴S4与旋转反映操作
• 注意: C4和与之垂直的σ都不独立存在
如果一物体有一Cn轴，并且有一对称面垂 直于此轴，则此轴Cn也是一个Sn轴。

S1
任何对称面都有一个垂直于它的S1轴

S2 i
F2
F3 F1
(a)
F2
(b)
分子中的四类对称操作 及相应的对称元素如下:
转 120 o
（1）n重对称轴与对称操作
物体有1个轴线，绕此轴旋转2Π/n弧度给出与原来位
置在物理上不可分辨的构型，就称此轴为n重对称轴, 符
号为Cn . 其操作为

Cn
180°
F1
F1

C2
B
B
F2
C2
F3 F3
F2
（2）对称面与反映操作
任何通过对称中心的轴是一个S2轴
对称面
v 面：包含主轴
h 面：垂直于主轴 d 面：包含主轴且平分相邻Cn2轴夹角
两个或多个对 称操作的乘积 必定也是一个 对称操作
例如,先作二重 旋转，再对垂 直于该轴的镜 面作反映，等 于对轴与镜面 的交点作反演.

年VIP
月VIP
连续包月VIP
VIP专享文档下载特权
享受60次VIP专享文档下载特权，一 次发放，全年内有效。
VIP专享文档下载特权自VIP生效起每月发放一次， 每次发放的特权有效期为1个月，发放数量由您购买 的VIP类型决定。
每月专享9次VIP专享文档下载特权， 自VIP生效起每月发放一次，持续有 效不清零。自动续费，前往我的账号 -我的设置随时取消。
4 霍夫型分岔
数学模型
dx
dt dy
y x[ (x2 x y[ (x2
y 2 )] y 2 )]
dt
引入极坐标
x2 y2
x cos
y
sin
求导
d
dt
(
2 )
d 1
dt
代入原方程
令正弦余弦系数 相等
dx ddyt
d
dt
d
cos cos
sin cos
2 转换键型分岔
相流
由分岔图可见，μ＜0或μ＞0都是一对鞍–结点： μ＜0时，x0=0 轴线是结点，x0= 是不稳定的； μ＞0时，x0=0 的轴线是不稳定的，x0= 是稳定结点。 由鞍点与稳定结点附近的相轨线流向，转换键型分岔的相流形 状如下图。
3 叉式分岔
数学模型
利用方程： dx x x3
二、从此点作水平线与对角线 相交，此交点横坐标即为x1；
三、再由此点作竖直线，得到 与抛物线相交时的高度x2，再 将x2移植到对角线上，找到横 坐标x2。从这里作竖直线与抛 物线相交得x3，如此反复······
1.平方映射
作图计算
平方映射 x n1 x n (1 x n ) 在 x n1 ~ x n 平面上是一条

分叉理论和方法对于含参数的系统，当参数变化并经过某些临界值时，系统的定性性态（如平衡态和或周期运动的数目和稳定性等）会发生突然变化，这种变化称为分叉。

分叉是重要非线性现象，与其它非线性现象（如混沌、突变、分形、拟序结构等）紧密相关。

主要研究：（a）相空间中轨线的集合；（b）控制参数空间中分叉集的性态。

分叉包括两类：（a）静态分叉：讨论平衡态数目和稳定性的变化，常见有：极限点分叉（鞍结分叉）、叉形分叉、跨临界分叉、滞后分叉、孤立点分叉等；（b）动态分叉：讨论系统在相空间中轨线拓扑结构的变化，常见有：Hopf分叉、次谐和超谐分叉、概（准）周期分叉（不变环面分叉）、同异宿轨线分叉等。

分叉问题起源于力学失稳现象的研究。

18世纪中叶，D.Bernoulli和L.Euler等人研究了杆件在纵向压力下的屈曲问题。

1834年C.G.J.Jacobi在研究自引力介质的椭球形旋转液体星的平衡图形时，首次引进“分叉”术语。

1885年，Poincare提出旋转液体星平衡图形演化过程的分叉理论。

1883年，O.Reynods发现在临界雷诺数时层流转变为湍流的现象，从此开创了流动稳定性的研究。

本世纪20年代，van der Pol 和安德罗诺夫等在非线性振动研究中即已发现大量分叉现象。

本世纪70年代形成分叉的数学理论和方法。

分叉揭示系统不同运动状态之间的联系和转化，且与失稳和混沌密切相关，是非线性动力学重要组成部分。

主要应用于：非线性振动、结构力学、流体力学、非线性波、飞行器动力学、机器人动力学、化学动力学、控制、非线性电学、非线性光学、生态学、经济学、交通动力学、转子动力学等等。

主要研究方法有：(1) 奇异性方法奇异性研究可微映射的退化性和分类，首先将分叉问题化为较简单的GS范式进行识别和分类，再通过“普适开折”得到一般扰动下可能出现的所有分叉性态，随后讨论分叉图的保持性和转迁集等。

可以处理：静态分叉、Hopf分叉和退化Hopf分叉。

I6包括6个对称动作。
第二第十二二十二页页，，课课件件共共有5有9页59页
I6 C3 h
22 22
第四章 分子的对称性
结论 In 包含的独立动作
Ø
当
n
为奇数时，I
包含
n
2n个对称动作，可由
Cn i
组成；
Ø 当 n为偶数时，
(1)
n
不是4的倍数时，
I
可由
n
Cn / 2 组h 成，包
含 n 个对称动作。
无
单
轴
轴
群
群
双
多
面
面
群
体 群
2021/12/23
31
2021/12/23
31
第三十一页，课件共有59页
第四章 分子的对称性
一、单轴或无轴群
⒈ Ci 群
O
OC
C
Fe
Fe
C
CO
O
对称元素： i Ci iˆ Eˆ h 2
2021/12/23
32
2021/12/23
32
第三第十三二十二页页，，课课件件共共有5有9页59页
第四章 分子的对称性
四、旋转反演操作(
Iˆn)和反轴(
I
)
n
1. 旋转反演操作( Iˆn)
这是一个联合操作，先依据某一直线旋转 Cˆ，n 然后按照轴上的中心点进行反演，Iˆn iˆCˆn 。
2. 反轴( In)
旋转反演操作依据的轴和对称中心称为反轴，In
的n决定于转轴的轴次。
2021/12/23
结合律
2021/12/23 2021/12/23
群中三个元素相乘有A(BC) (AB)C

C1 C2v
CCs1h
D3 D2h D2d
CSi2
Td Oh
典型类型
C2
C3
C3v
C∞v
C2h
C3h
D3h D3d
S4
D4h
D6h
D ∞h
1. Cn 点群
Cn群只有1个Cn 旋转轴。独立对称操作有n个。阶 次为n。
若分子只有n重旋转轴，它就属于Cn群，群元素为 {E，Cn1，Cn2…Cnn-1}。这是n阶循环群。
III. 1,3,5-三甲基苯
1,3,5-三甲基苯 （图III）是C3点 群的例子，若不考 虑甲基上H原子， 分子的对称性可以 很高，但整体考虑， C6H3(CH3)3只有C3 对称元素。C3轴位 于苯环中心，垂直 于苯环平面，分子 绕C3轴转动120°， 240°都能复原。
IV. CH3CCl3
如甲烷分子，一个
经过Ｃ原子的四次映转
轴S4，作用在分子上，H
１旋转到1’的位置后，
1’
经平面反映到H4的位置，
同时H2旋转到2’的位置
再反映到H3的位置……
整个分子图形不变，
S1 h ; S2 i ;
S C ; S 独立，包含C ;
3
3
h
4
2
S C ; S C i
5
5
h
6
3
即只有S4是独立的点群， 其余Sn 可化为 i, h 或 Cn i,Cn h
左图为D2对称性分子， C2主轴穿过联苯轴线，经过 2个O为水平面上的C2轴， 还有一个C2轴与这两个C2轴 垂直。
双乙二胺NH2CH2-CH2-NH2CH2-CH2-NH2可 对Co3+离子3配位 螯合，2个双乙二 胺与Co3+形成 Co(dien)2配合物， 具有D2对称性。 (右图）

例1. 全部整数的集合, 乘法规则为代数加法, 则构 成一个群.
恒等元素为 0. 数 n 的逆元素为 (-n). 封闭性和结合律是显然的.
例2. 数的集合 {1, -1, i, -i}, 乘法规则为代数乘法, 则构成一个群.
恒等元素为1. 数 (-1) 的逆元素为(-1).数 (i) 的逆元素为 (-i).
2. Sn 点群 (n为偶数) Sn ,S2n ,S3n ,....,Snn I S2 i
3. Cnv 点群 有一个 Cn 轴和 n 个包含该轴的对称面 v
Cv
4. Dn点群 有一个Cn轴和n个垂直于该轴的C2轴. (暂没有实例）
5. Cnh点群 有一个Cn轴和一个垂直于该轴的对称面h.
6. Dnd点群 有一个Cn轴,一个S2n轴, n个垂直于该轴 的C2轴, n个平分C2轴的对称面d.
y2
3 xy 2
A(d )z2 A C31 z2 C32z 2 z2
A(d )xy A C31 xy C31x C31y C32x C32 y
1 2
x
3 2
y
3 2
x
1 2
y
3 x2 4
3 y2 1 xy 42
A(d ) yz A C31 yz C31y C31z C32 y C32z
则称为群的表示.
（表示的乘积等于乘积的表示）
在三维空间中对称操作的矩阵表示.
1 0 0
E 0 1 0
0
0
1
1 0 0
xy 0 1 0
0
0
1
1 0 0
yz 0 1 0
0
0
1
1 0 0 i 0 1 0
0 0 1
cos sin 0

x
右手坐
标
z′ y′··y z
反射面
反射面
(b)
(c)
只左右对称 坐标系反射
根据镜象反射的性质可将物理学中的矢量
分成两类： 极矢量 和 轴矢量 4 第4页/共24页
极矢量：镜象反射中垂直反射面的分量反向，
平行反射面的分量不变向。
如：r，v，a，E ，
…
v′
v′ v
v
v′ v
v′
v
v′ v
反射面
5
第5页/共24页
22
第22页/共24页
参考书目
▲ 新概念物理教程《力学》赵凯华、罗蔚茵 ▲《对称》 H. Weyl 商务印书馆 1986 ▲《大学物理学》(第一册) 张三慧 主编 ▲ “Lecture on Physics” R.Feynman.
Vol.1
—完—
23
第23页/共24页
感谢您的观看！
24
第24页/共24页
南山长生松生长山南 南山长生松生长山南 8 第8页/共24页
④空间反演：
r
r
的操作称为对原点O
的空间反演。
x x
直角坐标系中的空间反演 y y
z z
空间反演不变的系统具有对O的点对称性。
例如，立方体对其中心具有点对称性。
反映空间反演对称性的物理量叫宇称 (parity)。
y′
x
空
镜面反射
z′ ·o
I = I1 +（I I1）
节点 C → D 的电流为：
I1 （I I1）= 2 I1 I
17
第17页/共24页
A I
I1
RC
(1)
R

(2) 甲烷具有S4，只有C2 与S4共轴，但C4和与之垂直 的σ并不独立存在.
CH4中的映轴S4与旋转反映操作
注意: C4和与之垂直的σ都不独立存在
环辛四烯衍生物中的 S4
分子中心是S4的图形符号
丙二烯
对称操作与对称元素
旋转是真操作, 其它对称操作为虚操作.
两个或多个对称 操作的结果，等效于 某个对称操作.
D2h群：乙烯
D3h 群
D3h 群 ： C2H6
D3h群分子多呈平面正三角形、正三棱柱或三角双锥结构
D4h群：XeF4
D6h群：苯
同核双原子分子，具有对称中心的线型分子，属于Dh群
Dh群： I3-
Dnd: 在Dn基础上, 增加了n个包含主轴且平分二次副轴
夹角的镜面σd.
D2d : 丙二烯
D2d : B2Cl4
3.偶次旋转轴和与它垂直的对称面的组合 一个偶次轴与一个垂直于它的对称面组合，必定在交
点上出现对称中心。 C2σh = S2 = i
3.2 点群
3.2.1定义一种称之为“乘
法”的运算，如果满足下列条件，则集合G构成群。
1）封闭性：集合G 中任何两个元素相“乘”（或称之为 组合），其结果仍然是G 中元素，也就是说，A、B分别 属于G，AB＝C 也属于G。即 A∈G， B∈G， 则 AB＝ C∈G
（2）二面体群：包括Dn、Dnh、Dnd . 这类点群的共同特点是
旋转轴除了主轴Cn外，还有与之垂直的n条C2副轴.
（a）Dn 群: 除主轴Cn外，还有与之垂直的n条C2副轴( 但没有 镜面).（ Cn + nC2⊥ Cn ）
D2 群
主轴C2垂直于荧光屏
D ： 3 这种分子比较少见，其对称元素也不易看出.

高中数学知识网络结构图第一部分 集合、映射、函数、导数及微积分集合映射 概念元素、集合之间的关系 运算：交、并、补 数轴、Venn 图、函数图象性质确定性、互异性、无序性 定义表示 解析法 列表法三要素图象法定义域对应关系值域 性质奇偶性周期性 对称性 单调性 定义域关于原点对称，在x ＝0处有定义的奇函数→f (0)＝01、函数在某个区间递增(或减)与单调区间是某个区间的含义不同；2、证明单调性：作差（商）、导数法；3、复合函数的单调性 最值二次函数、基本不等式、双钩（耐克）函数、三角函数有界性、数形结合、导数.幂函数 对数函数 三角函数基本初等函数抽象函数 复合函数 赋值法、典型的函数函数与方程 二分法、图象法、二次及三次方程根的分布 零点函数的应用 建立函数模型使解析式有意义 导数函数基本初等函数的导数导数的概念导数的运算法则导数的应用表示方法 换元法求解析式分段函数 几何意义(切线问题）、物理意义单调性导数的正负与单调性的关系生活中的优化问题注意应用函数的单调性求值域周期为T 的奇函数→f (T )＝f (T2)＝f (0)＝0 复合函数的单调性：同增异减三次函数的性质、图象与应用一次、二次函数、反比例函数指数函数图象、性质 和应用平移变换对称变换 翻折变换 伸缩变换图象及其变换最值极值第二部分 三角函数与平面向量角的概念 任意角的三角函数的定义 三角函数 弧度制 弧长公式、扇形面积公式三角函数线同角三角函数的关系 诱导公式 和角、差角公式 二倍角公式公式的变形、逆用、“1”的替换 化简、求值、证明（恒等变形）三角函数 的 图 象定义域奇偶性 单调性 周期性 最值对称轴（正切函数除外）经过函数图象的最高（或低）点且垂直x 轴的直线，对称中心是正余弦函数图象的零点，正切函数的对称中心为(k π2，0)（k ∈Z ）.正弦函数y ＝sin x= 余弦函数y ＝cos x 正切函数y ＝tan x y ＝A sin(ωx ＋ϕ)＋b①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；②图象也可以用五点作图法；③用整体代换求单调区间（注意ω的符号）； ④最小正周期T ＝2π| ω |；⑤对称轴x ＝(2k ＋1)π－2ϕ2ω，对称中心为(k π－ϕω，b )（k ∈Z ）. 平面向量 概念线性运算 基本定理 加、减、数乘几何意义坐标表示数量积几何意义模共线与垂直共线（平行）垂直 值域图象a →∥b →⇔b →＝λa → ⇔ x 1y 2－x 2y 1=0 a →⊥b →⇔b →·a →＝0 ⇔ x 1x 2＋y 1y 2=0解三角形余弦定理 面积 正弦定理 解的个数的讨论实际应用 S △＝12ah ＝12ab sin C ＝p (p －a )(p －b )(p －c )（其中p ＝a ＋b ＋c 2）投影b →在a →方向上的投影为|b →|cos θ＝a →·b→——|a →|设a →与b →夹角θ，则cos θ＝a →·b →——|a →|·|b →|对称性 |a →|＝(x 2－x 1)2＋(y 2－y 1)2夹角公式第三部分 数列与不等式概念 数列表示等差数列与等比数列的类比 解析法：a n ＝f (n )通项公式 图象法 列表法递推公式等差数列 通项公式 求和公式 性质 判断a n ＝a 1＋(n －1)d a n ＝a 1q n －1 a n ＋a m ＝a p ＋a r a n a m ＝a p a r 前n 项和 S n ＝n (a 1＋a n )2前n 项积(a n ＞0) T n ＝(a 1a n )n 常见递推类型及方法逐差累加法 逐商累积法 构造等比数列{a n ＋qp －1} 构造等差数列①a n ＋1－a n ＝f (n ) ②a n + 1a n＝f (n ) ③a n ＋1＝pa n ＋q ④pa n ＋1a n ＝a n －a n ＋1 化为a n ＋1q n =p q ·a nq n －1＋1转为③ ⑤a n + 1＝pa n ＋q n等比数列 a n ≠0，q ≠0 S n ＝⎩⎨⎧na 1，q ＝1a 1(1－q n)1－q ，q ≠1公式法：应用等差、等比数列的前n 项和公式 分组求和法 倒序相加法裂项求和法 错位相加法 常见求和方法不等式不等式的性质 一元二次不等式简单的线性规划 基本不等式：ab ≤a ＋b 2数列是特殊的函数借助二次函数的图象三个二次的关系可行域 目标函数一次函数：z ＝ax ＋by z ＝y －bx －a：构造斜率 z ＝(x －a )2＋(y －b )2：构造距离 应用题几何意义： z 是直线ax ＋by －z ＝0在x 轴截距的a 倍，y 轴上截距的b 倍.最值问题 变形 和定值，积最大；积定值，和最小 应用时注意：一正二定三相等 2aba ＋b≤ab ≤a ＋b 2≤a 2＋b 22倾斜角和斜率直线的方程位置关系直线方程的形式倾斜角的变化与斜率的变化重合平行相交垂直A1B2－A2B1＝0A1B2－A2B1≠0A1A2＋B1B2＝0点斜式：y－y0＝k(x－x0)斜截式：y＝kx＋b两点式：y－y1y2－y1＝x－x1x2－x1截距式：xa＋yb＝1一般式：Ax＋By＋C＝0注意各种形式的转化和运用范围.两直线的交点距离点到线的距离：d＝| Ax0＋By0＋C |A2＋B2，平行线间距离：d＝| C1－C2 |A2＋B2圆的方程圆的标准方程圆的一般方程直线与圆的位置关系两圆的位置关系相离相切相交∆＜0，或d＞r∆＝0，或d＝r∆＞0，或d＜r曲线与方程轨迹方程的求法：直接法、定义法、相关点法圆锥曲线椭圆双曲线抛物线定义及标准方程性质范围、对称性、顶点、焦点、长轴（实轴）、短轴（虚轴）、渐近线（双曲线）、准线（只要求抛物线）离心率对称性问题中心对称轴对称点(x1，y1) ───────→关于点(a，b)对称点(2a－x1，2b－y1)曲线f (x，y) ───────→关于点(a，b)对称曲线f (2a－x，2b－y)⎩⎪⎨⎪⎧A·x1＋x22＋B·y1＋y22＋C＝0y2－y1x2－x1·(－AB)＝－1特殊对称轴x±y＋C＝0 直接代入法截距注意：截距可正、可负，也可为0.点(x1，y1)与点(x2，y2)关于直线Ax＋By＋C＝0对称点与线空间点、 线、面的 位置关系点在直线上 点在直线外 点与面 点在面内 点在面外线与线共面直线异面直线相交平行没有公共点 只有一个公共点线与面平行相交有公共点没有公共点 直线在平面外直线在平面内面与面平行 相交平行关系的相互转化垂直关系的相互转化线线 平行线面 平行面面 平行线线 垂直线面 垂直面面 垂直空间的角异面直线所成的角 直线与平面所成的角 二面角 范围：(0︒，90︒] 范围：[0︒，90︒] 范围：[0︒，180︒]点到面的距离 直线与平面的距离 平行平面之间的距离相互之间的转化 cos θ＝|a →·b →|——|a →|·|b →|sin θ＝|a →·n →|——|a →|·|n →|cos θ＝n 1→·n 2→——|n 1→|·|n 2→|d ＝|a →·n →|——|n →|空间向量空间直角坐标系空间的距离 空间几何体柱体棱柱 圆柱 正棱柱、长方体、正方体台体 棱台 圆台 锥体 棱锥 圆锥球 三棱锥、四面体、正四面体直观图 侧面积、表面积 三视图体积长对正 高平齐 宽相等第六部分统计与概率统计随机抽样抽签法随机数表法简单随机抽样系统抽样分层抽样共同特点：抽样过程中每个个体被抽到的可能性（概率）相等用样本估计总体样本频率分布估计总体总体密度曲线频率分布表和频率分布直方图茎叶图样本数字特征估计总体众数、中位数、平均数方差、标准差变量间的相关关系两个变量的线性相关散点图回归直线正态分布列联表（2×2）独立性分析概率概率的基本性质互斥事件对立事件古典概型几何概型条件概率事件的独立性用随机模拟法求概率常用的分布及期望、方差随机变量两点分布X～B(1，p)E(X)＝p，D(X)＝p(1－p)二项分布X～B(n，p)E(X)＝np，D(X)＝np(1－p)定义概率的计算与分布列与二项分布的区别n次独立重复试验恰好发生k次的概率为P n(k)＝C k n p k(1－p)n－k超几何分布实际应用E（aX+b）=aE(X)+b2()()D aX b a D X+=P(A＋B)＝P(A)＋P(B)P(⎺A)＝1－P(A)P(A B)＝P(A)·P(B)P(B | A)＝P(A B)P(A)第七部分 其他部分内容合情推理演绎推理类比归纳 三段论 大前提，小前提，结论 两个原理分类加法计算原理和分步乘法计算原理 排列与组合 排列数：A m n ＝n !(n －m )!组合数：C m n ＝n !m !(n －m )!性质C m n ＝C n －mn C m n ＋1＝C m n ＋C m －1n计算原理二项式定理通项公式T r ＋1＝C r n a n －r b r首末两端“等距离”两项的二项式系数相等C 0n ＋C 2n ＋C 4n …＝C 1n ＋C 3n ＋C 5n …＝2n －1 C 0n ＋C 1n ＋…＋C n n ＝2n二项式系数性质 直接证明 综合法 分析法 由因导果 执果索因间接证明 反证法数学归纳法推理证明推理与证明充分非必要条件、必要非充分条件、充要条件关系条件复合命题 或：p ∨ q 且：p ∧ q 非：⌝ p应用原命题：若p 则q逆命题：若q 则p否命题：若⌝p 则⌝q逆命题：若⌝q 则⌝p互逆 互逆互否互否互为逆否 等价关系一真便真 一假则假全称量词与存在量词 简易逻辑概括性、逻辑性、有穷性、不唯一性、普遍性 顺序结构条件结构 循环结构命题算法语言算法的特征程序框图 基本算法语言算法案例 辗转相除法、更相减损术、秦九韶算法、进位制 复 数概念虚数、纯虚数、实部、虚部、实轴、虚轴、模、共轭复数 运算 加、减、乘、除、乘方几何意义与复平面内的点一一对应，其模表示到原点的距离。

C1h C1 h Cs
2n阶
H
Cl C C H
反式二氯己烯
Cl
C2h群
④ Dn群：
1个Cn轴加上n个垂直Cn的二重轴
（不存在任何对称面）
n1 (1) ( 2) ( n) Dn E, Cn ,Cn , C2 , C2 ,C2


2n阶
D3： [Co( NH 2CH 2CH 2 NH 2 )3 ]
(3)N2(直线形)
(4)CO
有σh、∞个σd(σv)
有∞ 个σv
⑤ 反轴In和旋转反演操作
如果分子图形绕轴旋转3600/n后，再按轴上的中 心点反演，可以产生分子的等价图形，则称该轴为反 轴，对应的对称操作为：I n iCn 例如CH4，其分子构型可用下图表示：
1 C4
i
CH4没有C4，但存在I4
一个有限分子的对称操作的集合构成群，称为分子点群。
2 分子点群的分类
分子的全部对称操作的集合构成群—分子点群， 采用Schonflies(熊夫利)记号。
① Cn群:
只有一个Cn轴。
2 n1 Cn E, Cn , Cn ,, Cn


n阶 C 1群 C 2群 C 3群
CHFClBr H2O2
1D=3.336×10-30c.m
偶极矩是分子本 身固有的性质，与是否有外加 电场无关。
-1-分子的偶极矩和分子的对称性
分子有无偶极矩与分子的对称性有密切关系。 对静态分子，可根据分子的对称性对分子有无 偶极矩作出简单明确的判据： 只有属于Cn和Cnv(n=1,2,3, …,∞) 点群的分子具 有偶极矩。C1v=C1h=Cs，Cs点群也包括在Cnv之 中。 具有对称中心的分子没有偶极矩；有两个对称 元素只相交于一点的分子偶极矩为零。