认识三角形1(1)
- 格式:ppt
- 大小:583.00 KB
- 文档页数:17

【学习目标】1.认识三角形,•能用符号语言表示三角形,并把三角形分类。
2.知道三角形任何两边的和大于第三边的性质。
3.懂得判断三条线段能否构成一个三角形的方法,并能用于解决有关的问题。
【学习重点、难点】三角形的三边关系及利用三边关系解决有关问题。
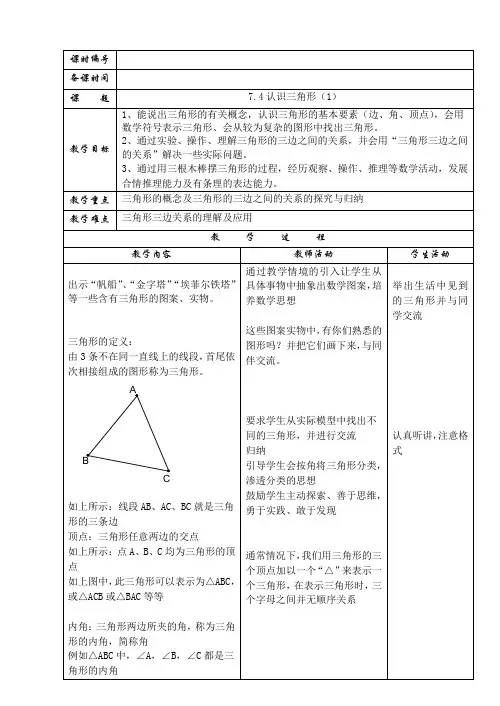
【学习过程】【课前自学,课中交流】阅读课本P4-5,完成下列内容知识点一:三角形概念及分类(1)三角形概念:由不在 直线上的三条 首尾顺次相接所组成的图形,叫做三角形。
如图1,线段BC 、___、___ 是三角形的边;三角形的三边也可以记为 , ,点A 、___、____是三角形的顶点;∠ABC 是____、_____相邻两边组成的角,叫做三角形的内角,简称三角形的角。
图中三角形的三个顶点为A 、B 、C,所以记作 ,读作 。
(2)小学我们学过,三角形的三个内角的和等于 。
(3)三角形按角分类可分为___ __ ____、___________、____________。
练习一:1.如图2.下列图形中是三角形的有______。
图22.图3中有 个三角形,用符号表示这些三角形为 。
3. 在△ABC 中,∠ABC =600,∠BCA =430,则∠C = 。
4.一个三角形最多有 个锐角,至少有 个锐角,最多有 个钝角,最多有 个直角。
知识点二:知道三角形三边的关系,并判断三条线段能否构成三角形?1.画一个△ABC ,分别量出AB ,BC ,AC 的长,并比较下列各式的大小: 图1主备人:潘群英 使用日期: 2013/9 审核人:______________AB=_______cm, BC=_________cm, CA=________cm;AB+BC_____AC AB+ AC _____ BC AC +BC _____ AB从中你可以得出结论: 三角形任意两边之和_________第三边问题:三角形任意两边之差与第三边长度比较大小?AB-AC____BC, AC-BC____AB, AB-BC____AC由上面得到结论:三角形任意两边之差_________第三边练习二:1.模仿书本例1的格式试完成下题:下列长度的三条线段能否组成三角形?为什么?(1)3,4,8; (2)5,6,11; (3)5,6,102.ΔABC 中,三边长分别为4,7,c,则 < c <3.如果三角形的两边长分别是3和5,那么第三边长可能是( )A 、1B 、9C 、3D 、104. 一个三角形有两条边相等,周长为20cm ,三角形的一边长6cm ,求其他两边长。






1.1 认识三角形(1)【教学目标】1、通过实践活动,理解三角形三个内角的和等于180o2、理解三角形的一个外角等于和它不相邻的两个内角的和3、合适用三角形的内角和外角的性质简单的几何问题4、了解三角形的分类【教学重点、难点】1.本节教学的重点是三角形三个内角和等于180o的性质是本节重点。
2.例3是立体图形,涉及的角之间的关系不易辨认,是本节难点。
【教学过程】1,合作学习:①请每个学生利用手中的三角形(已备),把三角形的三个角撕(或剪)下来,然后把这三个角拼起来,然后观察这三个角拼成了一个什么角?②请学生归纳这一结论,教师板书:三角形的三个内角的和等于180O2、三角形内角和性质的应用①口答:△ABC中,∠A=45O,∠B=60O,求∠C②△ABC中,∠A=57O18,,∠B=46O49,。
求∠C③△ABC中,∠A=∠B,∠C=110O,求∠A,∠B④△ABC中,∠A:∠B:∠C=1:2:3,求这个三角形的三个内角。
3、由上题得出图中三角形的形状①②得出的三角形的三个角都是锐角,这样的三角形称之为锐角三角形③得出的三角形有一个角是钝角,这样的三角形称之为钝角三角形④得出的三角形有一个角是直角,这样的三角形称之为直角的三角形若一个三角形为Rt△,那么它的其余两个锐角互余。
4、三角形的外角:①定义:三角形的一边和另一边相邻边组成的角,叫做三角形的外角。
由图得:∠BCE+∠ACB=180O而∠A+∠B+∠ACB=180O∴∠BCE=∠A+∠B从而得到定理:三角形的一个外角等于和它不相邻的两个内角的和②外角也并不一定绝对,要会看一个角之是内角还是外角。
5、练习:1)△ABC中,∠ACD=120O∠A=50O ,求∠B、∠ACD2)如书本例题3),已知,在△ABC 中, ∠C=Rt ∠,D 是BC 上一点,已知∠1=∠2,∠B=25O ,求∠BAD 数。
6:小结:角形的内角和性质②认识三角形的外角的概念,并能准确寻找外角和内角 7,布置作业1.1 认识三角形(2)【教学目标】1、使学生知道三角形的角平分线和中线的定义,并能熟练地画出这两种线段 2、能应用三角形的角平分线和中线的性质解决简单的数学问题 【教学重点、难点】教学重点、难点:三角形的角平分线、中线的定义及画图是本节课的重点,利用三角形的角平分线和中线的性质解决有关的计算问题是本节难点。


第1章三角形的初步知识1.1 认识三角形(一)(第1题)1.如图,图中共有__6__个三角形,以AD为边的三角形有△ABD,△ADE,△ADC,以E为顶点的三角形有△ABE,△ADE,△AEC,∠ADB是△ABD的内角,△ADE的三个内角分别是∠ADE,∠AED,∠DAE.2.三角形的两边长分别是2和3,若第三边的长是奇数,则第三边的长为__3__;若第三边的长是偶数,则三角形的周长为7或9.3.在现实生活中,有些人为抄近路而践踏了草坪,这是一种不文明的现象,我们应予以制止或劝解.请你用数学知识解释这一现象的原因:两点之间线段最短.4.(1)已知在△ABC中,AB=6,BC=4,则边AC的长可能是(B)A. 11B. 5C. 2D. 1(2)若等腰三角形中有两边长分别为2和5,则这个三角形的周长为(B)A. 9B. 12C. 7或9D. 9或125.在三个内角互不相等的△ABC中,最小的内角为∠A,则在下列四个度数中,∠A最大可取(B)A. 30°B. 59°C. 60°D. 89°6.若一个三角形三个内角的度数之比是2∶3∶7,则这个三角形一定是(C)A. 直角三角形B. 锐角三角形C. 钝角三角形D. 不能确定(第7题)7.如图,在△BCD中,BC=4,BD=5.(1)求CD的取值范围.(2)若AE∥BD,∠A=55°,∠BDE=125°,求∠C的度数.【解】(1)∵在△BCD中,BC=4,BD=5,∴1<CD<9.(2)∵AE∥BD,∠BDE=125°,∴∠AEC=55°.又∵∠A=55°,∴∠C=180°-∠AEC-∠A=70°.8.若a,b,c是三角形的三边长,则化简|a-b-c|+|a+c-b|-|c-a-b|=(B)A. 3a-b-cB. -a-b+3cC. a+b+cD. a-3b+c【解】∵a+b>c,b+c>a,a+c>b,∴原式=b+c-a+a+c-b-a-b+c=-a -b+3c.9.三角形纸片上有100个点,连同三角形的顶点共103个点,其中任意三点都不共线.现以这些点为顶点作三角形,并把纸片剪成小三角形,则这样的三角形共有201个.【解】从最大的三角形纸片计数,任意选中纸片内一点,沿顶点与该点连线剪开,可以得到3个小三角形,即增加了2个小三角形.同理,再从中任取一点,剪开,也是增加了2个三角形,因此每多取一个点,三角形就增加2个,所以共有100×2+1=201(个)三角形.10.各边长都是整数,且最大边长为8的三角形共有多少个?【解】∵各边长度都是整数、最大边长为8,∴三边长可以为:1,8,8;2,7,8;2,8,8;3,6,8;3,7,8;3,8,8;4,5,8;4,6,8;4,7,8;4,8,8;5,5,8;5,6,8;5,7,8;5,8,8;6,6,8;6,7,8;6,8,8;7,7,8;7,8,8;8,8,8.故各边长都是整数,且最大边长为8的三角形共有20个.(第11题)11.在农村电网改造中,四个自然村分别位于如图所示的A,B,C,D处,现计划安装一台变压器,使到四个自然村的输电线路的总长最短,那么这个变压器应安装在AC,BD 的交点E处,你知道这是为什么吗?【解】如图,另任取一点E′(异于点E),分别连结AE′,BE′,CE′,DE′.在△BDE′中,DE′+BE′>D B.在△ACE′中,AE′+CE′>A C.∴AE′+BE′+CE′+DE′>AC+BD,即AE+BE+CE+DE最短.12.观察并探求下列各问题:(1)如图①,在△ABC中,P为边BC上一点,则BP+PC__<__AB+AC(填“>”“<”或“=”).(2)将(1)中的点P移到△ABC内,得图②,试观察比较△BPC的周长与△ABC的周长的大小,并说明理由.(3)将(2)中的点P变为两个点P1,P2,得图③,试观察比较四边形BP1P2C的周长与△ABC 的周长的大小,并说明理由.(第12题)【解】(1)BP+PC<AB+A C.理由:三角形两边的和大于第三边.(2)△BPC的周长<△ABC的周长.理由如下:如解图①,延长BP交AC于点M.在△ABM中,BP+PM<AB+AM,在△PMC中,PC<PM+MC,两式相加,得BP+PC<AB+AC,∴BP+PC+BC<AB+AC+BC,即△BPC的周长<△ABC的周长.(第12题解)(3)四边形BP1P2C的周长<△ABC的周长.理由如下:如解图②,分别延长BP1,CP2交于点M.由(2)知,BM+CM<AB+A C.又∵P1P2<P1M+P2M,∴BP1+P1P2+P2C<BM+CM<AB+AC,∴BP1+P1P2+P2C+BC<AB+AC+BC,即四边形BP1P2C的周长<△ABC的周长.。
1课题:7.4认识三角形(1)(总第6课时) 课型:新授学习目标:1.认识三角形的概念及其基本要素,并能用符号语言表示三角形及其基本要素.2.能正确区分锐角三角形、直角三角形、钝角三角形,体悟分类的数学思想.3.理解三角形三边之间的关系,并能用于解决相关的问题;提高自主探究的能力,增强学好数学的信心.学习重点:三角形的概念及三角形的三边之间的关系的探究与归纳,发展推理能力及表达能力. 学习难点:三角形三边关系的应用.导学过程:【预习交流】1.预习课本P20到P21,记下你的疑惑.2.△ABC 是△DEF 经过平移得到的,若AD =4cm ,则BE = __ cm ,=__ cm ,若M 为AB 的中点,N 为DE 的中点,则MN = cm 3.下列各组长度的3条线段,不能构成三角形的是( )A.3cm 8cm. 10cmB.5cm 4cm 9cmC.4cm 6cm 9cmD.2cm 3cm 4cm4.一个等腰三角形的两边长分别是6cm 和9cm ,则它的周长是 .【点评释疑】1.课本P20节头图,举出生活中见到的三角形.由3条不在同一直线上的线段,首尾依次相接组成的图形称为三角形.三角形的基本元素:顶点 用大写字母表示.例如:A B C归纳: (内)角 用一个大写字母或三个大写字母表示. 例如:∠A,∠ABC边 用两个大写字母或一个小写字母表示. 例如:BC a注意:在表示的时候要注意角与边的对应.∠A ←→a 边(BC ) ∠B ←→b 边(AC ) ∠C ←→c 边(AB )以A 、B 、C 为顶点的三角形可以表示为△ABC ,或△ACB 或△BAC.2.课本P20议一议.三角形的分类(1)按角分:三角形(2)按边分:三角形3.课本P21数学实验室.结论:三角形的任意两边之和大于第三边;4.应用探究(1)小丽在纸上画了四点,如果把这些点彼此用线段连结,连成一个图形,则图形中有几个三角形?并把它们一一表示出来. (2)一个等腰三角形的两边分别为3和6,求这个三角形的周长.(3)做一做:分别量出如图锐角三角形的三边的长度,并填到横线上. ①a = b = c =②计算三角形的任意两边之差,并与第三边比较 B C E a b c A B C2a-b c , c-b a , c-a b ,③你有什么发现吗?④对于直角三角形和钝角三角形,按照上面的研究方法,继续探究,你有什么发现?(4)有两根长度分别为4cm 和7cm 的木棒,①用长度为2cm 的木棒与它们能摆成三角形吗?为什么?②长度为11cm 的木棒呢?③长度为4cm 的木棒呢?④什么长度范围的木棒, 能与原来的两根木棒摆成三角形?(5)△ABC 三边的长a ,b ,c 都是整数,且a >b >c ,a =8,问:满足条件的三角形共有多少个?(6)有3条线段,其长度分别为a 、a +4、a +6(a >0),请问这3条线段能否组成三角形? 5巩固练习:课本P21练习1、2.【达标检测】1.小晶有两根长度为5cm 、8cm 的木条,她想钉一个三角形的木框,现在有长度分别为2cm 、3cm 、 8cm 、15cm 的木条供她选择,那她第三根应选择( )A.2cmB.3cmC.8cmD.15cm 2.等腰三角形的一边长为3㎝,另一边长是5㎝,则它的第三边长为 .3.等腰三角形的一边长为2㎝,另一边长是5㎝,则它的第三边长为 .4.如图,以∠C 为内角的三角形有 和在这两个三角形中,∠C 的对边分别为 和5.下图中有几个三角形,分别用字母把它们表示出来,说明是什么三角形,6.如图:有A 、B 、C 、D 四个村庄,打算公用一个水厂,若要使用的水管最节约,水厂应建在村庄的什么地方?7.已知△ABC 中,a =2,b =4,第三边c 为偶数,求c 的值.8.有长度分别为2cm,3cm,4cm 和5cm 的小木棒各两根..,任取其中3根,你可以搭出几种不同..的三角形?【总结评价】1.三角形的概念及三角形的基本要素,三角形的分类.2.三角形的三边互相制约——三角形的任意两边之和大于第三边.【课后作业】课本P23习题7.4 1、2、3.A B C D · · · · D C。