初中数学精品说题稿：抛物线解题

中考数学压轴题专题一：利用抛物线中的角度求点的坐标（原创）二次函数中的角度问题通常要构造直角、相似、全等三角形把角度问题转化为边的问题，求抛物线中的点坐标方法一般采用两种方法，第一种是求线与线的交点，这时需要联立方程；第二种是几何法，过点做坐标轴的垂线，再利用三角函数或者是相似三角形去求解！例1.抛物线y＝﹣x2+x+4与坐标轴分别交于A，B，C三点，P是第一象限内抛物线上的一点且横坐标为m．连接CP，是否存在点P，使得∠BCO+2∠PCB＝90°，若存在，求m 的值，若不存在，请说明理由．解题思路：1.利用∠BCO+2∠PCB＝90°和∠BCO+∠CBO＝90°推出∠CBO=2∠PCB2.得出∠CMB=∠MCB得到BC=BM3.求出M的坐标，进而求出直线CM的直线解析式4.联立直线CM方程和抛物线方程，求交点坐标例2.已知抛物线y＝x2+x﹣3与x轴交于点A（1，0）和点B两点，与y轴交于点C，点P是抛物线点第三象限上一动点（不与点A，B，C重合），作PD⊥x轴，垂足为D，连接PC．且∠CPD＝45°，求点P的坐标；解题思路：45度可以联想到等腰直角三角形1.延长PC交x轴于点E，得出等腰直角三角形2.求出E点坐标，进而求出直线CE的解析式3.联立直线CE方程和抛物线方程，求交点坐标例3.抛物线y＝x2﹣4x与直线y＝x交于原点O和点B，与x轴交于另一点A，顶点为D．连接OD，P为x轴上的动点，当tan∠PDO＝时，求点P的坐标；解题思路1.分情况讨论，分P在原点的左右侧进行讨论2.P在原点右侧比较简单3.P在原点左侧要结合P在原点右侧的情况，可以得出等腰△OGD，求出G点坐标4.利用GD的直线直线方程或相似三角形求出P点坐标例4.已知抛物线y＝﹣x2﹣6x﹣5与x轴交于点A（﹣1，0）和B（﹣5，0），与y轴交于点C，顶点为P，点N在抛物线对称轴上且位于x轴下方，连AN交抛物线于M，连AC、CM．tan ∠ACM＝2时，求M点的横坐标；解题思路：1.构造一线三垂直利用相似求出点F坐标2.求出直线CF的解析式3.联立直线CF方程和抛物线方程，求交点坐标（求交点可以利用韦达定理）例5.在平面直角坐标系中，抛物线y＝x2﹣2x﹣3与x轴交于点A（﹣1，0）和点B，与y轴交于点C，顶点D的坐标为（1，﹣4）．点P在抛物线上且满足∠PCB＝∠CBD，求点P 的坐标；解题思路：1.分情况讨论，P在直线BC的上方和下方2.P在直线BC上方，利用∠PCB＝∠CBD得出PC平行BD，利用斜率相等求出直线PC解析式联立PC方程和抛物线方程，求交点坐标3.P在直线BC的下方，∠PCB＝∠CBD得出等腰三角形CFB，4.可以得出△BCD为直角三角形，，推出F为BD的中点5.求出直线CF的方程，再联立抛物线方程求出交点坐标例6.如图，在平面直角坐标系中，直线y＝﹣x+2与x轴交于点A，与y轴交于点B，抛物线经过A，B两点且与x轴的负半轴交于点C．点D为直线AB上方抛物线上的一个动点，当∠ABD＝2∠BAC时，求点D的坐标；解题思路：1.过点B做OA平行线2.∠ABD＝2∠BAC得出∠ABD=2∠EBA，得出∠FBD=∠BAC3.利用tan∠FBD=tan∠BAC求出D点做坐标例7.已知抛物线y＝（x﹣1）2，D为抛物线的顶点，直线y＝kx+4﹣k与抛物线交于P、Q两点．求证：∠PDQ＝90°；解题思路思路1.构造一线三垂直思路2.证明直线PD和直线DQ斜率之积为-1思路3.利用勾股定理逆定理证明例8.如图，抛物线y＝x2﹣2x﹣6与x轴交于A、B两点，与y轴交于点C，其对称轴交抛物线于点D，交x轴于点E，已知OB＝OC＝6．连接BD，F为抛物线上一动点，当∠F AB ＝∠EDB时，求点F的坐标；解题思路：1.分点F在x轴下方时和上方时进行分类讨论2.AB在x轴上，利用tan∠FAB＝tan∠EDB去求最简便例9.如图，已知抛物线C1：交x轴于点A，B，交y轴于点C．在抛物线上存在点D，使，求点D的坐标．解题思路：1.分D在BC上方和下方讨论2.找到特殊点发现tan∠OBC=3.利用角平分线的性质去求F坐标4.求联立直线BF和抛物线方程求D点坐标例10，平面直角坐标系中，已知抛物线y＝﹣x2+5x﹣4与x轴交于点A，B两点（点A在点B左边），与y轴交于点C．D为抛物线x轴上方一点，连接BD，若∠DBA+∠ACB＝90°，求点D的坐标；解题思路：利用tan∠ACB=tan∠FDB去求解例11.已知抛物线y＝﹣x2﹣x+2，BC平分∠PCO时，求点P的横坐标．解题思路：1.角平分线联想到角平分线＋平行线得到等腰三角形2.利用PE=PC去求解（两点之间的距离公式）例12.抛物线y＝x2﹣1，M（﹣4，3），N是抛物线上两点，N在对称轴右侧，且tan∠OMN ＝，求N点坐标；解题思路：构造一线三垂直课后练习1.在平面直角坐标系中，已知抛物线y＝ax2+4ax+4a﹣6（a＞0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．直线DC交x轴于点E，tan∠AED＝，求a的值和CE的长；2.已知抛物线y＝（x+1）2+1，点A（﹣1，2）在抛物线的对称轴上。

变一变，更精彩——一道习题的说题稿新课程标准倡导“以学生为主体，教师为主导”，数学教学离不开例题习题，而教学中如何选择例题习题，从而挖掘教材潜在的智能价值，充分展示教学功能，并使课本知识有效地浓缩。

通过不同角度、不同层次、不同情形、不同背景的变式，使一题多变，从而揭示不同知识点的联系，使学生加深知识的理解与内化，使知识系统化，克服某些思维定势，发散学生思维，培养学生思维的灵活性、全面性和创新性，提高学生解决实际问题和应变的能力。

我们今天要讲的这个题目是：如图，抛物线2y x=与直线12y x=相交于O，A两点，点P沿着抛物线从点A出发，按横坐标大于点A的横坐标方向运动，PS∥x轴，交直线OA于点S，PQ⊥x轴，SR⊥x轴，垂足为Q，R．（1）当点P的横坐标为2时，回答下面问题：①求S点的坐标．②求通过原点，且平分矩形PQRS面积的直线解析式．（2）当矩形PQRS为正方形时，求点P的坐标．一、题目总体分析这是一个难度系数中等的一个综合题，它的重点是动态几何与二次函数、一次函数相结合的综合训练，具体内容是几何图形在运动状态下函数性质的运用。

难点是在解动点问题时，如何做到明确运动状态下各个变量、各个点之间的内在联系，如P点在抛物线上运动时，P、S的坐标之间的联系。

随着点P的位置变化，矩形PQRS的形状也在变化，在矩形PQRS的形状变化过程中，如何用一条直线将它平分等。

讲解之前不仅要明确解题思路，解题过程中要用到的数学定理、性质，相关知识点，更要了解学生对这块内容的掌握程度，审题要点。

尤其要做到循序渐进，层层深入，知识之间的自然过渡。

二、温故引新，实现知识的铺垫1．你能用一条直线将矩形分成面积相等的两部分吗？能画多少条？这些直线有什么特征？答：有无数条，并且它们都经过矩形的对称中心。

[设计意图]通过本题复习矩形对称中心的有关性质。

2．（1） 如图1中，已知矩形ABCO ，B(4,6),求点D 的坐标。

（2） 如图2中，已知矩形ABCE,E(a ，0),B(4+a,6),求点D 的坐标。

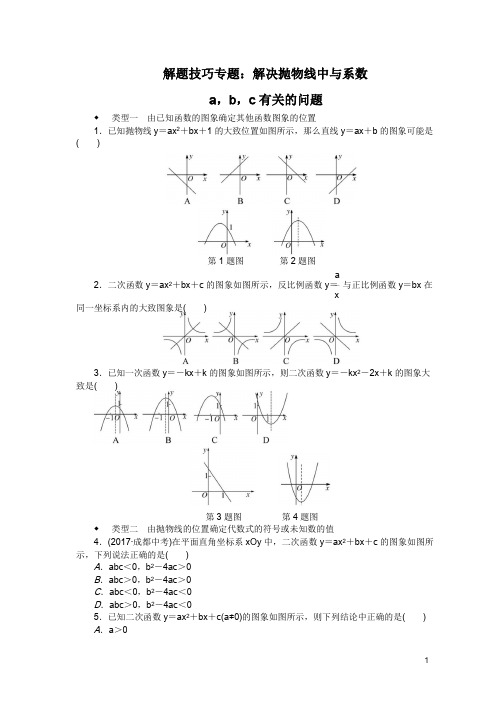
解题技巧专题：解决抛物线中与系数a ，b ，c 有关的问题◆ 类型一 由已知函数的图象确定其他函数图象的位置1．已知抛物线 y ＝ax 2＋bx ＋1 的大致位置如图所示，那么直线 y ＝ax ＋b 的图象可能是( )第 1 题图 第 2 题图a2．二次函数 y ＝ax 2＋bx ＋c 的图象如图所示，反比例函数 y ＝与正比例函数 y ＝bx 在 x同一坐标系内的大致图象是( )3．已知一次函数 y ＝－kx ＋k 的图象如图所示，则二次函数 y ＝－kx 2－2x ＋k 的图象大 致是( )第 3 题图 第 4 题图◆ 类型二 由抛物线的位置确定代数式的符号或未知数的值4．(2017·成都中考)在平面直角坐标系 xOy 中，二次函数 y ＝ax 2＋bx ＋c 的图象如图所 示，下列说法正确的是( )A ．abc ＜0，b 2－4ac ＞0B ．abc ＞0，b 2－4ac ＞0C ．abc ＜0，b 2－4ac ＜0D ．abc ＞0，b 2－4ac ＜05．已知二次函数 y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，则下列结论中正确的是( ) A ．a ＞01B．c＜0C．3 是方程ax2＋bx＋c＝0 的一个根D．当x＜1 时，y 随x 的增大而减小第5 题图第6 题图6．(2017·烟台中考)二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，对称轴是直线x＝1，下列结论：①ab＜0；②b2＞4ac；③a＋b＋2c＜0；④3a＋c＜0.其中正确的是() A．①④B．②④C．①②③D．①②③④7．(2017·营口一模)函数y＝x2＋bx＋c 与y＝x 的图象如图所示，有以下结论：①b2－4c ＞0；②b＋c＋1＝0；③3b＋c＋6＝0；④当1＜x＜3 时，x2＋(b－1)x＋c＜0.其中正确的是________(填序号)．8．二次函数y＝ax2＋bx＋c 的图象如图所示，且P＝|2a＋b|＋|3b－2c|，Q＝|2a－b|－|3b ＋2c|，比较P，Q 的大小关系．参考答案与解析1．A2b 2．C解析：由y＝ax2＋bx＋c的图象开口向下，对称轴在y轴右侧，得a＜0，－＞2aa0，∴b＞0，∴反比例函数y＝的图象位于第二、四象限，正比例函数y＝bx的图象位于第x一、三象限．故选C.13．B解析：由一次函数的图象可知k＞1，∴－k＜0，－1<－<0，∴抛物线开口向下，k对称轴在直线x＝－1 与y轴之间，与y轴的交点在(0，1)的上方．故选B.4．B 5.C 6.C7．③④解析：∵二次函数y＝x2＋bx＋c与x轴无交点，∴b2－4ac＜0，故①错误；当x＝1 时，y＝1＋b＋c＝1，故②错误；∵当x＝3 时，y＝9＋3b＋c＝3，∴3b＋c＋6＝0，故③正确；∵当1＜x＜3 时，二次函数值小于一次函数值，∴x2＋bx＋c＜x，∴x2＋(b－1)x＋c＜0，故④正确．故正确的为③④.b8．解：∵抛物线的开口向下，对称轴在y轴右侧，∴a＜0，－＞0，∴b＞0，∴2a－2ab 1 1b＜0.∵－＝1，∴2a＋b＝0，a＝－b.当x＝－1 时，y＝a－b＋c＜0，∴－b－b＋c＜0，2a 2 2∴3b－2c＞0.∵抛物线与y轴的正半轴相交，∴c＞0，∴3b＋2c＞0，∴P＝|2a＋b|＋|3b－2c|＝3b－2c，Q＝|2a－b|－|3b＋2c|＝b－2a－3b－2c＝－2a－2b－2c，∴Q－P＝－2a－2b－2c－3b＋2c＝－2a－5b＝－4b＜0，∴P＞Q.3。

初中数学抛物线中必知的六大结论由二次函数y=ax2+bx+c(a≠0）的图象确定系数a、b、c以及相应的关系式，一般是给出3-6个结论，然后判断正确结论的个数或选出正确的结论，要解决此类问题，需要祭出一件制胜法宝——数形结合思想！下面就带你见识一下数形结合思想在解题时如何大显神威：1.由抛物线开口方向确定a2.由对称轴的位置确定b、ab3.由抛物线与y轴的交点位置确定c4.由抛物线与x轴的交点个数确定b2-4ac5.由对称轴为x=±1时确定2a±b6.特殊式子集锦真题反馈:1.（2018•遂宁）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则以下结论同时成立的是（）A．B．C．D．2.（2018•白银）如图是二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的一部分，与x轴的交点A在点（2，0）和（3，0）之间，对称轴是x=1．对于下列说法：①ab＜0；②2a+b=0；③3a+c＞0；④a+b≥m（am+b）（m为实数）；⑤当﹣1＜x＜3时，y＞0，其中正确的是（）A．①②④B．①②⑤C．②③④D．③④⑤3.（2018•达州）如图，二次函数y=ax2+bx+c的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，2）与（0，3）之间（不包括这两点），对称轴为直线x=2．下列结论：①abc＜0；②9a+3b+c＞0；③若点M（，y1），点N（，y2）是函数图象上的两点，则y1＜y2；④﹣＜a＜﹣．其中正确结论有（）A．1个 B．2个 C．3个 D．4个4.（2018•衡阳）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标（1，n）与y轴的交点在（0，2），（0，3）之间（包含端点），则下列结论：①3a+b＜0；②﹣1≤a≤﹣；③对于任意实数m，a+b≥am2+bm总成立；④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根．其中结论正确的个数为（）A．1个 B．2个 C．3个 D．4个5.（2018•枣庄）如图是二次函数y=ax2+bx+c图象的一部分，且过点A（3，0），二次函数图象的对称轴是直线x=1，下列结论正确的是（）A．b2＜4ac B．ac＞0 C．2a﹣b=0 D．a﹣b+c=06.（2018•大庆）如图，二次函数y=ax2+bx+c的图象经过点A（﹣1，0）、点B （3，0）、点C（4，y1），若点D（x2，y2）是抛物线上任意一点，有下列结论：①二次函数y=ax2+bx+c的最小值为﹣4a；②若﹣1≤x2≤4，则0≤y2≤5a；③若y2＞y1，则x2＞4；④一元二次方程cx2+bx+a=0的两个根为﹣1和其中正确结论的个数是（）A．1 B．2 C．3 D．47.（2018•随州）如图所示，已知二次函数y=ax2+bx+c的图象与x轴交于A、B 两点，与y轴交于点C对称轴为直线x=1．直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1．其中正确的有（）8. 二次函数2y ax bx c =++（0a ≠）的图象如图所示，下列结论：①20a b +>；②0abc <；③240b ac ->；④0a b c ++<；⑤420a b c -+<，其中正确的个数是（ ）A ．2B ．3C ．4D ．59. 二次函数2y ax bx c =++（0a ≠）的图象如图所示，下列说法：①20a b +=， ②当13x -≤≤时，0y <，③若（1x ，1y ）、（2x ，2y ）在函数图象上，当12x x <时，12y y <，④930a b c ++=，其中正确的是（ ）A ．①②④B ．①④C ．①②③D ．③④10. 如图，抛物线2y ax bx c =++（0a ≠）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，设P =a b c ++，则P 的取值范围是（ ）A ．﹣3＜P ＜﹣1B ．﹣6＜P ＜0C ．﹣3＜P ＜0D ．﹣6＜P ＜﹣3 11. 已知二次函数2y ax bx c =++的图象如图所示，记2m a b c a b c =-++++， 2n a b c a b c =+++--．则下列选项正确的是（ ）A ．m n <B ．m n >C ．m n =D ．m 、n 的大小关系不能确定 12. 已知二次函数2y ax bx c =++（0a ≠）的图象如图所示，① abc >0，②a 3>b 2，③()m am b a b +≤-（m 为任意实数），④c b a +-24<0，以下结论中正确的个数是（ ） A ．1 B ．2 C ．3 D ．4。

中考数学抛物线动点题秒杀技巧全文共四篇示例，供读者参考第一篇示例：抛物线是数学中一个非常重要的概念，也是中考数学考试中常常会出现的题型之一。

抛物线的性质不仅仅是个别的知识点，更是一个整体的系统性知识。

在解题过程中，我们需要灵活运用抛物线的相关知识，抓住关键点，掌握一些技巧，才能在考试中取得更好的成绩。

本文将为大家介绍一些中考数学抛物线动点题的秒杀技巧，希望能够帮助大家顺利解答相关题目。

我们需要了解抛物线的基本性质。

抛物线是一种特殊的二次曲线，其一般方程为y=ax^2+bx+c，其中a、b、c为常数，a≠0。

抛物线开口的方向取决于a的正负性：当a>0时，抛物线开口向上；当a<0时，抛物线开口向下。

在抛物线上，我们常常遇到顶点、焦点、准线等概念，这些都是解题过程中需要重点关注的内容。

在解决抛物线动点题时，我们首先要确定动点的位置。

动点通常是抛物线上的一个点，在运动过程中其坐标会发生变化。

设抛物线的方程为y=ax^2+bx+c，动点的坐标为(x,y)，我们需要根据题目中的条件，确定动点的位置。

我们需要利用抛物线的性质，建立动点坐标变化的关系式。

在解题过程中，我们常常需要根据已知条件列方程，利用抛物线的性质建立动点坐标变化的关系式，从而求解动点的轨迹、移动方向等。

如果动点在抛物线上以匀速运动，我们可以利用速度的定义建立关于动点坐标的变化式。

我们需要灵活运用数学知识，解题过程中要注意化繁为简。

在解决抛物线动点题时，我们可能会遇到复杂的条件和问题，这时我们需要善于化繁为简，抓住关键点，简化问题。

可以通过几何、代数等不同的方法，灵活运用数学知识，解题过程中要注意逻辑性，不要陷入死胡同。

中考数学抛物线动点题并不是难题，关键在于掌握抛物线的基本性质，灵活运用数学知识，化繁为简，善于建立关系式，抓住关键点。

通过不断练习，积累经验，相信大家能够在考试中轻松应对抛物线动点题，取得好成绩。

希望以上的技巧能够帮助大家更好地掌握抛物线动点题的解题方法，祝大家在中考数学考试中取得优异成绩！第二篇示例：中考数学中，抛物线动点题是考生普遍认为比较难的题型之一。

中考数学抛物线动点题秒杀技巧
中考数学中关于抛物线动点题目的解题关键在于，首先要理解抛物线的性质，包括其方程、顶点、对称轴等。

然后，根据题目给出的条件，选择适当的公式或方法来求解。

对于抛物线上的动点问题，通常需要找到与动点相关的量，如距离、角度等，并使用这些量建立方程或不等式。

在解题过程中，可能还需要使用一些基本的数学技能，如代数运算、几何作图和推理等。

以一道题目为例：在平面直角坐标系中，点A的坐标为(1,0)，点B的坐标为(0,2)，点C的坐标为(4,0)，动点P在x轴上运动，当∠APB最大时，求点P的坐标。

首先，需要确定∠APB的最大值。

根据三角形内角和为180°的性质，∠APB=180°-∠APO-∠BPO。

因为∠APO和∠BPO的大小与点P的位置有关，所以当∠APB 最大时，必然有∠APO和∠BPO尽可能小。

根据题目条件，可以找到当OA=PB 时，∠APB最大。

接下来，设点P的坐标为(x,0)，根据OA=PB，可以得到方程x^2+1=x-4+2，
解得x=-1或x=3。

由于题目要求∠APB最大，所以点P的坐标应为(3,0)。

解决抛物线上的动点问题需要综合运用抛物线的性质、三角形的性质、代数运算和几何作图等技能。

在解题过程中，要善于根据题目条件建立方程或不等式，并灵活运用各种数学技能来求解。

解题技巧专题：解决抛物线中 与系数a ，b ，c 有关的问题◆类型一 由某一函数的图象确定其他函数图象的位置【方法5】1．一次函数y ＝ax ＋b (a ≠0)与二次函数y ＝ax 2＋bx ＋c (a ≠0)在同一平面直角坐标系中的图象可能是( )2．若二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则直线y ＝abx ＋c 的图象不经过( ) A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限第2题图 第3题图 第4题图3．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，则一次函数y ＝ax ＋b 与反比例函数y ＝cx 在同一平面直角坐标系内的图象大致为( )4．★如图，一次函数y 1＝x 与二次函数y 2＝ax 2＋bx ＋c 的图象相交于P ，Q 两点，则函数y ＝ax 2＋(b －1)x ＋c 的图象可能是( )◆类型二 由抛物线的位置确定代数式的符号或未知数的值5．二次函数y ＝ax 2＋bx ＋c 的图象如图所示，下列结论：①4ac <b 2；②a ＋c >b ；③2a ＋b >0.其中正确的有( )A ．①②B ．①③C ．②③D ．①②③6．(2017·成都中考)在平面直角坐标系xOy 中，二次函数y ＝ax 2＋bx ＋c 的图象如图所示，下列说法正确的是( )A ．abc ＜0，b 2－4ac ＞0B ．abc ＞0，b 2－4ac ＞0C ．abc ＜0，b 2－4ac ＜0D ．abc ＞0，b 2－4ac ＜07．如图是二次函数y ＝ax 2＋bx ＋c 图象的一部分，图象过点A (－3，0)，对称轴为直线x ＝－1，给出下列4个结论：①c >0；②若点B ⎝⎛⎭⎫－32，y 1，C ⎝⎛⎭⎫－52，y 2为函数图象上的两点，则y 1<y 2；③2a －b ＝0；④4ac －b 24a<0.其中正确结论的个数是( ) A ．1个 B ．2个 C ．3个 D ．4个第7题图 第8题图8．(2017·安顺中考)二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图所示，给出下列4个结论：①4ac －b 2＜0；②3b ＋2c ＜0；③4a ＋c ＜2b ；④m (am ＋b )＋b ＜a (m ≠－1)．其中正确结论的个数是( )A ．1个B ．2个C ．3个D ．4个9．★二次函数y ＝ax 2＋bx ＋c 的图象如图所示，且P ＝|2a ＋b |＋|3b －2c |，Q ＝|2a －b |－|3b ＋2c |，试判断P ，Q 的大小关系．参考答案与解析1．C 2.D 3.B4．A 解析：∵一次函数y 1＝x 与二次函数y 2＝ax 2＋bx ＋c 的图象相交于P ，Q 两点，∴方程ax 2＋(b －1)x ＋c ＝0有两个不相等的根，分别为点P ，Q 的横坐标x P ，x Q .∴函数y ＝ax 2＋(b －1)x ＋c 的图象与x 轴有两个交点，分别为(x P ，0)，(x Q ，0)．∵x P ＞0，x Q ＞0，∴选项A 符合条件．故选A.5．B 6.B 7．B 解析：由抛物线交y 轴于正半轴，可知c >0，故①正确；∵对称轴为直线x ＝－1，抛物线开口向下，－52<－32<－1，∴y 1>y 2，故②错误；∵对称轴为直线x ＝－1，∴－b2a ＝－1，即2a －b ＝0，故③正确；由函数图象可知抛物线最高点的纵坐标大于0，∴4ac －b 24a >0，故④错误．综上所述，正确的结论有2个．故选B.8．C 解析：∵图象与x 轴有两个交点，∴方程ax 2＋bx ＋c ＝0有两个不相等的实数根，∴b 2－4ac ＞0，∴4ac －b 2＜0，∴①正确；∵－b2a ＝－1，∴b ＝2a .∵当x ＝1时，y ＜0，即a＋b ＋c ＜0，∴12b ＋b ＋c ＜0，∴3b ＋2c ＜0，∴②是正确；∵当x ＝－2时，y ＞0，∴4a －2b＋c ＞0，∴4a ＋c ＞2b ，∴③错误；∵由图象可知当x ＝－1时该二次函数取得最大值，∴a －b ＋c ＞am 2＋bm ＋c (m ≠－1)，∴m (am ＋b )＋b ＜a (m ≠－1)，∴④正确．∴正确的结论有①②④.故选C.9．思路点拨：先根据图象判断出2a ＋b ，3b －2c ，2a －b ，3b ＋2c 的正负，然后将P ，Q 去绝对值，再用作差法来比较两数的大小．解：∵抛物线的开口向下，∴a ＜0.∵－b 2a ＞0，∴b ＞0，∴2a －b ＜0.∵－b2a＝1，∴b ＋2a ＝0.当x ＝－1时，y ＝a －b ＋c ＜0，∴－12b －b ＋c ＜0，∴3b －2c ＞0.∵抛物线与y 轴的正半轴相交，∴c ＞0，∴3b ＋2c ＞0，∴P ＝3b －2c ，Q ＝b －2a －3b －2c ＝－2a －2b －2c ，∴Q －P ＝－2a －2b －2c －3b ＋2c ＝－2a －5b ＝－4b ＜0.∴P ＞Q .。

抛物线习题精选精讲（1）抛物线——二次曲线的和谐线椭圆与双曲线都有两种定义方法，可抛物线只有一种：到一个定点和一条定直线的距离相等的所有点的集合.其离心率e=1，这使它既与椭圆、双曲线相依相伴，又鼎立在圆锥曲线之中.由于这个美好的1，既使它享尽和谐之美，又生出多少华丽的篇章.【例1】P 为抛物线px y 22=上任一点，F 为焦点，则以PF 为直径的圆与y 轴（ ）.A 相交 .B 相切 .C 相离 .D 位置由P 确定【解析】如图，抛物线的焦点为,02p F ⎛⎫⎪⎝⎭，准线是 :2pl x =-.作PH ⊥l 于H ，交y 轴于Q ，那么PF PH =， 且2pQH OF ==.作MN ⊥y 轴于N 则MN 是梯形PQOF 的中位线，()111222MN OF PQ PH PF =+==.故以PF 为直径的圆与y 轴相切，选B.【评注】相似的问题对于椭圆和双曲线来说，其结论则 分别是相离或相交的.（2）焦点弦——常考常新的亮点弦有关抛物线的试题，许多都与它的焦点弦有关.理解并掌握这个焦点弦的性质，对破解这些试题是大有帮助的.【例2】 过抛物线()022 p px y =的焦点F 作直线交抛物线于()()1122,,,A x y B x y 两点，求证： （1）12AB x x p =++ （2）pBF AF 211=+ 【证明】（1）如图设抛物线的准线为l ，作1AA l ⊥11111,2pA BB l B AA x ⊥==+于，则AF ， 122pBF BB x ==+.两式相加即得：12AB x x p =++（2）当AB ⊥x 轴时，有AF BF p ==，112AF BF p∴+=成立； 当AB 与x 轴不垂直时，设焦点弦AB 的方程为：2p y k x ⎛⎫=- ⎪⎝⎭.代入抛物线方程：l XY FA(x,y)11B(x,y)22A 1B 1l2222p k x px ⎛⎫-= ⎪⎝⎭.化简得：()()222222014p k x p k x k -++=∵方程（1）之二根为x 1，x 2，∴1224k x x ⋅=.()122111212121111112224x x p p pp p AF BF AA BB x x x x x x +++=+=+=+++++ ()()121222121222424x x p x x p p p p pp x x p x x ++++===+++++. 故不论弦AB 与x 轴是否垂直，恒有pBF AF 211=+成立.（3）切线——抛物线与函数有缘有关抛物线的许多试题，又与它的切线有关.理解并掌握抛物线的切线方程，是解题者不可或缺的基本功.【例3】证明：过抛物线22y px =上一点M （x 0，y 0）的切线方程是：y 0y=p （x+x 0）【证明】对方程22y px =两边取导数：22.py y p y y''⋅=∴=，切线的斜率 00x x p k y y ='==.由点斜式方程：()()20000001p y y x x y y px px y y -=-⇒=-+20021y px =，代入（）即得： y 0y=p （x+x 0）（4）定点与定值——抛物线埋在深处的宝藏抛物线中存在许多不不易发现，却容易为人疏忽的定点和定值.掌握它们，在解题中常会有意想不到的收获.例如：1.一动圆的圆心在抛物线x y 82=上，且动圆恒与直线02=+x 相切，则此动圆必过定点（ ）()()()().4,0.2,0.0,2.0,2A B C D -显然.本题是例1的翻版，该圆必过抛物线的焦点，选B. 2.抛物线22y px =的通径长为2p ；3.设抛物线22y px =过焦点的弦两端分别为()()1122,,,A x y B x y ，那么：212y y p =-以下再举一例【例4】设抛物线22y px =的焦点弦AB 在其准线上的射影是A 1B 1，证明：以A 1B 1为直径的圆必过一定点【分析】假定这条焦点弦就是抛物线的通径，那么A 1B 1=AB=2p ，而A 1B 1与AB 的距离为p ，可知该圆必过抛物线的焦点.由此我们猜想：一切这样的圆都过抛物线的焦点.以下我们对AB 的一般情形给于证明.【证明】如图设焦点两端分别为()()1122,,,A x y B x y ，那么：22121112.y y p CA CB y y p =-⇒⋅==设抛物线的准线交x 轴于C ，那么.CF p =2111111.90A FB CF CA CB A FB ∴∆=⋅∠=︒中故.这就说明：以A 1B 1为直径的圆必过该抛物线的焦点.● 通法 特法 妙法（1）解析法——为对称问题解困排难 解析几何是用代数的方法去研究几何，所以它能解决纯几何方法不易解决的几何问题（如对称问题等）. 【例5】（07.四川文科卷.10题）已知抛物线y=-x 2+3上存在关于直线x+y=0对称的相异两点A 、B ，则|AB|等于（ ）A.3B.4C.32D.42【分析】直线AB 必与直线x+y=0垂直，且线段 AB 的中点必在直线x+y=0上，因得解法如下.【解析】∵点A 、B 关于直线x+y=0对称，∴设直线AB的方程为：y x m =+. 由()223013y x mx x m y x =+⎧⇒++-=⎨=-+⎩设方程（1）之两根为x 1，x 2，则121x x +=-. 设AB 的中点为M （x 0，y 0），则120122x x x +==-.代入x+y=0：y 0=12.故有11,22M ⎛⎫- ⎪⎝⎭. 从而1m y x =-=.直线AB 的方程为：1y x =+.方程（1）成为：220x x +-=.解得：2,1x =-，从而1,2y =-，故得：A （-2，-1），B （1，2）.AB ∴=，选C.（2）几何法——为解析法添彩扬威虽然解析法使几何学得到长足的发展，但伴之而来的却是难以避免的繁杂计算，这又使得许多考生对解析几何习题望而生畏.针对这种现状，人们研究出多种使计算量大幅度减少的优秀方法，其中最有成效的就是几何法.【例6】（07.全国1卷.11题）抛物线24y x =的焦点为F ，准线为l ，经过FXYAB FA 1B 11M C XOY ABMl x y +=ÿ物线在x 轴上方的部分相交于点A ，AK l ⊥，垂足为K ，则AKF △的面积（ ）A ．4 B． C． D ．8 【解析】如图直线AFAFX=60°. △AFK 为正三角形.设准线l 交x 轴于M ，则2,FM p ==且∠KFM=60°，∴24,44AKFKF S ∆===选C. 【评注】（1）平面几何知识：边长为a 的正三角形的面积用公式2S ∆=计算. （2）本题如果用解析法，需先列方程组求点A 的坐标，，再计算正三角形的边长和面积.虽不是很难，但决没有如上的几何法简单.（3）定义法——追本求真的简单一着许多解析几何习题咋看起来很难.但如果返朴归真，用最原始的定义去做，反而特别简单. 【例7】（07.湖北卷.7题）双曲线22122:1(00)x y C a b a b-=>>，的左准线为l ，左焦点和右焦点分别为1F 和2F ；抛物线2C 的线为l ，焦点为21F C ；与2C 的一个交点为M ，则12112F F MF MF MF -等于（ ）A ．1-B ．1C ．12-D ．12【分析】 这道题如果用解析法去做，计算会特别繁杂，而平面几何知识又一时用不上，那么就从最原始的定义方面去寻找出路吧.如图，我们先做必要的准备工作：设双曲线的半 焦距c ，离心率为e ，作 MH l H ⊥于，令1122,MF r MF r ==.∵点M 在抛物线上，1112222,MF MF rMH MF r e MH MF r ∴=====故，这就是说：12||||MF MF 的实质是离心率e.其次，121||||F F MF 与离心率e 有什么关系？注意到： ()1212111122111F F e r r c e a e e MF r r r e +⋅⎛⎫====-=- ⎪⎝⎭. XY O F(1,0)AK60°Y2=2px L:x=-1M这样，最后的答案就自然浮出水面了：由于()12112||||11||||F F MF e e MF MF -=-+=-.∴选 A..（4）三角法——本身也是一种解析三角学蕴藏着丰富的解题资源.利用三角手段，可以比较容易地将异名异角的三角函数转化为同名同角的三角函数，然后根据各种三角关系实施“九九归一”——达到解题目的.因此，在解析几何解题中，恰当地引入三角资源，常可以摆脱困境，简化计算.【例8】（07.重庆文科.21题）如图，倾斜角为a 的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点。