专题:力的正交分解法讲解 训练
- 格式:doc
- 大小:1.34 MB
- 文档页数:4

力的正交分解限时训练 1.如图所示,甲、乙、丙三个物体质量相同,与地面的动摩擦因数相同,受到三个大小相同的作用力F ,当它们滑动时,受到的摩擦力大小是( )A .甲、乙、丙所受摩擦力相同B .甲受到的摩擦力最小C .乙受到的摩擦力最小D .丙受到的摩擦力最大【答案】B 【详解】甲、乙、丙三个物体中,甲对地面的正压力最小,乙对地面的正压力最大,所以甲受到的摩擦力最小,乙受到的摩擦力最大,故B 正确。
故选B 。
2.如图所示,质量为m 的物体,在恒力F 作用下沿天花板匀速直线运动,物体与顶板间的动摩擦因数为μ,则物体受到的摩擦力大小为( ) A .cos F θ B .sin F θB .C .()sin mg F μθ+D .()sin mg F μθ-【答案】A【详解】以物体为对象,水平方向根据受力平衡可得cos f F θ=竖直方向根据受力平衡可得sin N F mg θ=-由于摩擦力为滑动摩擦力,则有(sin )f N F mg μμθ==-故选A 。
3.质量为5kg 的物块放在水平地面上,在大小为10N 水平向右拉力1F 作用下恰好可以拉动物块。
若改用与水平方向成37角斜向右上方的拉力2F 作用,该物块可以在水平地面上匀速滑动。
(设最大静摩擦力等于滑动摩擦力,g 取210m /s ,sin370.6,cos370.8==)求:(1)物块与地面间的动摩擦因数μ;(2)拉力2F 的大小;(3)物块匀速滑动时对地面的压力。
(结果小数点后保留一位数字)【答案】(1)0.2;(2)10.9N ;(3)43.4N ,方向竖直向下【详解】(1)大小为10N 水平向右拉力1F 作用下恰好可以拉动物块,根据平衡条件有1f N F F F mg μμ===物块与地面间的动摩擦因数0.2μ=(2)若改用拉力2F 作用,根据平衡条件有2cos37F f =物块与地面间摩擦力为2(sin 37)f mg F μ=-解得2250N 10.9N 23F ≈= (3)物块匀速滑动时,地面对物块的支持力为2sin 3743.4N N mg F =-≈根据牛顿第三定律物块匀速滑动时对地面的压力为43.4N N N '==方向竖直向下。

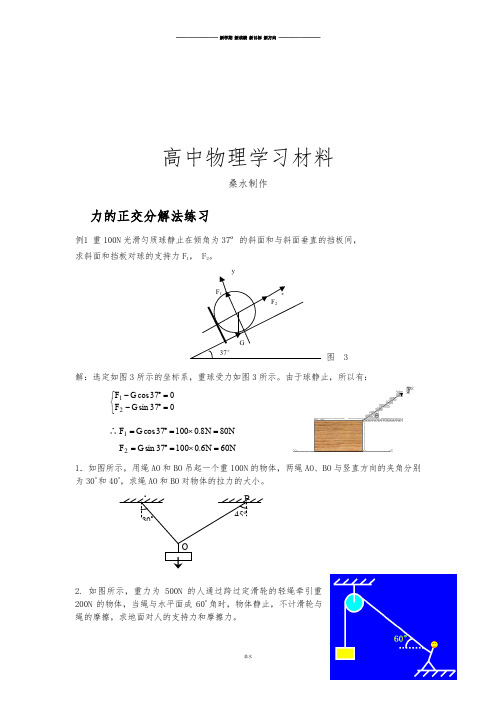
30o 45o A B O高中物理学习材料桑水制作力的正交分解法练习例1 重100N 光滑匀质球静止在倾角为37º的斜面和与斜面垂直的挡板间,求斜面和挡板对球的支持力F 1, F 2。
yF 1 xF 2G 37° 图 3解:选定如图3所示的坐标系,重球受力如图3所示。
由于球静止,所以有:⎩⎨⎧=︒-=︒-037sin 037cos 21G F G F ∴N N G F 808.010037cos 1=⨯=︒=N N G F 606.010037sin 2=⨯=︒=1.如图所示,用绳AO 和BO 吊起一个重100N 的物体,两绳AO 、BO 与竖直方向的夹角分别为30o 和40o ,求绳AO 和BO 对物体的拉力的大小。
2. 如图所示,重力为500N 的人通过跨过定滑轮的轻绳牵引重200N 的物体,当绳与水平面成60o 角时,物体静止,不计滑轮与绳的摩擦,求地面对人的支持力和摩擦力。
3. (8分)如图6所示,θ=370,sin370=0.6,cos370=0.8。
箱子重G =200N ,箱子与地面的动摩擦因数μ=0.30。
要匀速拉动箱子,拉力F 为多大?4.(8分)如图,位于水平地面上的质量为M 的小木块,在大小为F 、方向与水平方向成a 角的拉力作用下沿地面作匀速直线运动。
求:(1) 地面对物体的支持力?(2)木块与地面之间的动摩擦因数?5.(6分)如图10所示,在倾角为α=37°的斜面上有一块竖直放置的档板,在档板和斜面之间放一个重力G=20N 的光滑球,把球的重力沿垂直于斜面和垂直于档板的方向分解为力F 1和F 2,求这两个分力F 1和F 2的大小。
6..如图所示,在倾角为θ的粗糙斜面上,有一个质量为m 的物体被水平力F 推着静止于斜面上,已知物体与斜面间的动摩擦因数为μ,且μ<tan θ,若物体恰好不下滑,则推力F 为多少?若物体恰好不上滑,则推力F 为多少? (最大静摩擦力等于滑动摩擦力)7..(2010·齐河月考)所受重力G 1=8 N 的砝码悬挂在绳PA 和PB 的结点上.PA 偏离竖直方向37°角,PB 在水平方向,且连在所受重力为G 2=100 N 的木块上,木块静止于倾角为37°的斜面上,如图所示,试求:(1)木块与斜面间的摩擦力;(2)木块所受斜面的弹力.8.如图所示,板A的质量为m,滑块B的质量为2m,板A用绳拴住,绳与斜面平行,滑块B沿倾角为α的斜面在A板的中间一段匀速下滑,若A、B之间以及B与斜面间的动摩擦因数相同,求动摩擦因数μ。

专题:力的正交分解法1、定义:把力沿着两个选定的互相垂直的方向分解,叫做力的正交分解法。
说明:正交分解法是一种很有用的方法,尤其适于物体受三个或三个以上的共点力作用的情怳。
2、正交分解的原理一条直线上的两个或两个以上的力,其合力可由代数运算求得。
当物体受到多个力的作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便。
为此,我们建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴上,求x 、y 轴上的合力Fx, FyFx=F X1+F X2+F X3+、、、 F Y =F Y1+F Y2+F Y3+、、、④最后求Fx 和Fy 的合力F 大小 :方向(与Y 方向的夹角):分别求出两个不同方向上的合力F x 和F y ,然后就可以由F 合=22y x F F +,求合力了。
说明:“分”的目的是为了更方便的“合”正交分解与常规力的分解的区别:正交分解与力的分解不同的是不是按照力的作用效果分解,而是把力分解成相互垂直的两个分力,任然按照平行四边形定则分解。
基本思想:等效替代。
正交分解法的步骤:(1)以力的作用点为原点作直角坐标系,标出x 轴和y 轴,如果这时物体处于平衡状态,则两轴的方向可根据方便自己选择。
(2)将与坐标轴不重合的力分解成x 轴方向和y 轴方向的两个分力,并在图上标明,用符号F x 和F y 表示。
(3)在图上标出力与x 轴或力与y 轴的夹角,然后列出F x 、F y 的数学表达式。
如:F 与x 轴夹角为θ,则F x =Fcos θ,F y =Fsin θ。
与两轴重合的力就不需要分解了。
(4)列出x 轴方向上的各分力的合力和y 轴方向上的各分力的合力的两个方程,然后再求解。
例1 三个力共同作用在O 点,如图6所示,F 1、F 2与F 3之间的夹角均为600,求合力。
解析:此题用正交分解法既准确又简便,以O 点为原点,F 1为x轴建立直角坐标; (1)分别把各个力分解到两个坐标轴上,如图7所示:0;111==y x F F F0222260sin ;60cos F F F F y o x ==图6F 1F 2F 303303360sin ;60cos F F F F y x =-=(2)然后分别求出 x 轴和y 轴上的合力cos60F -cos60F F F F F 030213X 2X 1X +=++=合XF sin60F sin60F 0F F F 03023y 2y 1y =++=++=合y F (3)求出F x 和F y 如图8所示。


专题:力的正交分解法
1、定义:把力沿着两个选定的互相垂直的方向分解,叫做力的正交分解法。
说明:正交分解法是一种很有用的方法,尤其适于物体受三个或三个以上的共点力作用的情怳。
2、正交分解的原理
一条直线上的两个或两个以上的力,其合力可由代数运算求得。
当物体受到多个力的作用,并且这几个力只共面不共线时,其合力用平行四边形定则求解很不方便。
为此,我们建立一个直角坐标系,先将各力正交分解在两条互相垂直的坐标轴上,求x 、y 轴上的合力Fx, Fy
Fx=F X1+F X2+F X3+、、、 F Y =F Y1+F Y2+F Y3+、、、
④最后求Fx 和Fy 的合力F 大小 :
方向(与Y 方向的夹角):
分别求出两个不同方向上的合力F x 和F y ,然后就可以由F 合=2
2y x F F +,求合力了。
说明:“分”的目的是为了更方便的“合”
正交分解与常规力的分解的区别:正交分解与力的分解不同的是不是按照力的作用效果分解,而是把力分解成相互垂直的两个分力,任然按照平行四边形定则分解。
基本思想:等效替代。
正交分解法的步骤:
(1)以力的作用点为原点作直角坐标系,标出x 轴和y 轴,如果这时物体处于平衡状态,则两轴的方向可根据方便自己选择。
(2)将与坐标轴不重合的力分解成x 轴方向和y 轴方向的两个分力,并在图上标明,用符号F x 和F y 表示。
(3)在图上标出力与x 轴或力与y 轴的夹角,然后列出F x 、F y 的数学表达式。
如:F 与x 轴夹角为θ,则F x =Fcos θ,F y =Fsin θ。
与两轴重合的力就不需要分解了。
(4)列出x 轴方向上的各分力的合力和y 轴方向上的各分力的合力的两个方程,然后再求解。
例1 三个力共同作用在O 点,如图6所示,F 1、F 2与F 3之间的夹角均为600,求合力。
解析:此题用正交分解法既准确又简便,以O 点为原点,F 1
为
x
轴建立直角坐标; (1)分别把各个力分解到两个坐标轴上,如图7所示:
0;111==y x F F F
0222260sin ;60cos F F F F y o x ==
图6
F 1
F 2
F 3
03303360sin ;60cos F F F F y x =-=
(2)然后分别求出 x 轴和y 轴上的合力
cos60F -cos60F F F F F 030213X 2X 1X +=++=合X
F sin60F sin60F 0F F F 03023y 2y 1y =++=++=合y F (3)求出F x 和F y 如图8所示。
F F F 2F 2
y 2x =+=合合合
0Y 603F ===θθ;既合
合X F
tg ,则合力与F 1的夹角为600
运用正交分解法解题时,x 轴和y 轴方向的选取要根据题目给出的条件合理选取,即让受力物体受到的各外力尽可能的与坐标轴重合,这样方便解题 。
运用正交分解法解平衡问题时,根据平衡条件F 合=0,应有ΣF x =0,ΣF y =0,这是解平衡问题的必要和充分条件,由此方程组可求出两个未知数。
例2 重100N 光滑匀质球静止在倾角为37º的斜面和与斜面垂直的挡板间, 求斜面和挡板对球的支持力F 1, F 2。
解:选定如图3所示的坐标系,重球受力如图3所示。
由于球静止,所
以有:
⎩⎨
⎧=︒-=︒-037sin 0
37cos 2
1G F G F ∴N N G F 808.010037cos 1=⨯=︒=
N N G F 606.010037sin 2=⨯=︒= 图3
例3、如图所示,用绳AC 和BC 吊起一个重100N 的物体,两绳AC 、BC 与竖直方向的夹角分别为30°和45°。
求:绳AC 和BC 对物体的拉力的大小。
解:此题可以用平行四边形定则求解,但因其夹角不是特殊角,计算麻烦,如果改用正交分解法计算简便得多。
先以C 为原点作直角坐标系,设x 轴水平,y 轴竖直,在图上标出F AC 和在x 轴和y 轴上的分力。
即:
F ACx =________________; F ACy =________________
F BCx =________________;F BCy =________________
在x 轴上,F ACx F BCx 大小相等,即________________(1)
F 图8
在y轴上,F ACy与F BCy的合力与重力相等
即________________(2)
解(1)(2)得绳BC的拉力
F BC=________________
绳AC的拉力F AC=________________
巩固练习
1.如图5所示:三个共点力,F1=5N,F2=10N,F3=15N,θ=60°,它们
的合力的x轴方向的分量F x为________N,y轴方
向的分量F y为N,合力的大小为N,合力方
向与x轴正方向夹角为。
2. (8分)如图6所示,θ=370,sin370=0.6,cos370=0.8。
箱子重G=200N,箱子与地面的
动摩擦因数μ=0.30。
要匀速拉动箱子,拉力F为多大?
3.(8分)如图,位于水平地面上的质量为M的小木块,在大小为F、方向与水平方向成a 角的拉力作用下沿地面作匀速直线运动。
求:
(1)地面对物体的支持力?
(2)木块与地面之间的动摩擦因数?
4.(6分)如图10所示,在倾角为α=37°的斜面上有一块竖直放置的档板,在档板和斜面之间放一个重力G=20N的光滑球,把球的重力沿垂直于斜面和垂直于档板的方向分解为力
F1和F2,求这两个分力F1和F2的大小。
5.(6分)长为20cm 的轻绳BC 两端固定在天花板上,在中点系上一重60N 的重物,如图10所示:
(1)当BC 的距离为10cm 时,AB 段绳上的拉力为多少?
(2)当BC 的距离为102cm 时.AB 段绳上的拉力为多少?
6.如图所示重20N 的物体在斜面上匀速下滑,斜面的倾角为37°,求: (1)物体与斜面间的动摩擦因数。
(2)要使物体沿斜面向上匀速运动,应沿斜面向上施加一个多大的推力?
(sin37°=0.6, cos37°=0.8 )
7.如图所示,物体A 质量为2kg ,与斜面间摩擦因数为0.4若要使A 在斜面上静止,物体B 质量的最大值和最小值是多少?。