2019年福建省永春县初一数学竞赛试题

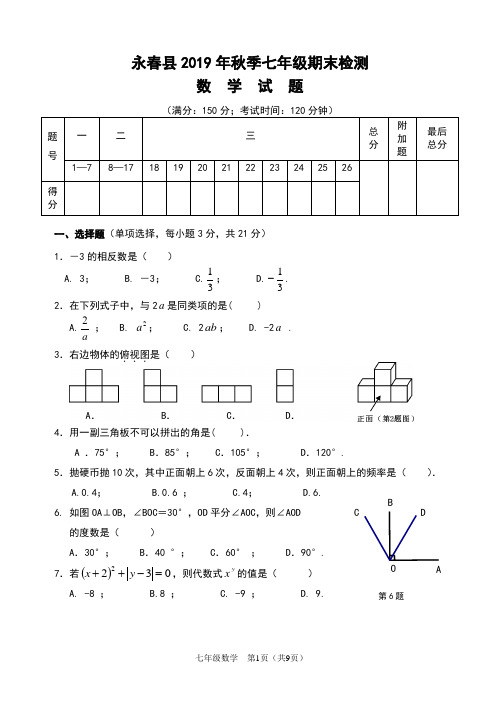
永春县2019年秋季七年级期末检测数 学 试 题一、选择题（单项选择，每小题3分，共21分） 1．－3的相反数是（ ） A. 3； B. －3； C.31； D.31-. 2．在下列式子中，与2a 是同类项的是( ) A.a2 ； B. 2a ； C. 2ab ； D. -2a . 3．右边物体的俯视图．．．是（ ）4．用一副三角板不可以拼出的角是( )．A ．75°；B ．85°；C ．105°；D ．120°.5．抛硬币抛10次，其中正面朝上6次，反面朝上4次，则正面朝上的频率是（ ）．A.0.4；B.0.6 ；C.4；D.6. 6. 如图OA ⊥OB ，∠BOC ＝30°，OD 平分∠AOC ，则∠AOD 的度数是（ ）A ．30°；B ．40 °；C ．60° ；D ．90°. 7．若()0322=-++y x ，则代数式yx 的值是（ ）A. -8 ；B.8 ；C. -9 ；D. 9.A ．B ．C ．D ．第6题CDBOA二、填空题（每小题4分，共40分） 8．-2的绝对值是 ．9．地球离太阳约为150 000 000千米，用科学记数法表示为 千米． 10．用代数式表示“a 的3倍与4的和 ”为 . 11．用“＜”号或“＞”号填空： -3 4.12．把多项式32432x x x ++-按x 的降幂排列 ． 13．若∠1和∠2互为余角，且∠1＝50°,则∠2＝ °．14．下面是一个简单的数值运算程序框图，当输入x 的值为3时，输出的数值是 .15．一副没有大小王的扑克牌，共有52张，任抽一张恰为黑桃的机会是 .16．一楼梯共有n 级台阶，规定每步可以迈1级台阶或2级台阶或3级台阶，设从地面到第n 级台阶所有不同的走法为M 种. （1）当n =2时，M= 种； （2）当n =7时，M= 种.17．图1是一个边长为2的等边三角形和一个四边均长为1的四边形的组合图形，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼 下去（如图3），…，则第1个图形的周长是 ；第4个图形的周长是 .图1图2图3……输入x输出+4三、解答题（共89分） 18．（12分）计算241214161⨯--）（2243435-÷+-）（19．（第小题6分，共12分）（1）化简：()()x x x x 72315322+-+--（2）先化简，再求值： )23(2)2(322xy x xy x ---，其中2-=x ，3-=y ．20．（8分）已知线段AB,在方格纸上画出以下图形．(1) 画∠ABC=45º；(2) 在（1）的条件下，过点A 画AD ⊥BC,垂足为D ．21．（8分）某校为了解该校学生的课余活动情况，从阅读、运动、娱乐、其它四个方面调查了若干名学生的爱好，经统计整理，绘制成不完整的扇形统计图与条形统计图 如下，请回答如下问题： (1)本次共调查了多少人？ (2)把条形统计图补充完整； (3)求其它所在扇形的圆心角的度数.22．（8分）如图，∠B=55°，∠EAC=110°，AD 平分∠EAC ，AD 与BC 平行吗？为什么？根据下面的解答过程，在括号内填空或填写理由. 解：∵AD 平分∠EAC ，∠EAC=110°（已知） ∴∠EAD ＝21∠ EAC ＝ ° ∵∠B ＝55°（已知）∴∠B ＝∠（ ） （ ） ∴AD ∥BC （ ）其它娱乐 35% 运动 20%阅读CDE B A动学生课余活动情况条形统计图乐它读23．（8分）政府引导农民对生产的土特产进行加工后，分为甲、乙、丙三种不同包装这三种不同的包装的土特产都销售了120千克，那么本次销售中，那一种包装的 土特产获得的利润最大，最大利润是多少？24．（9分）直线AB 、CD 被直线EF 所截，EF 分别交AB 、CD 于M ，N,∠EMB=50°,MG 平分∠BMF,MG 交CD 于G ．（1）如图1，若AB ∥CD ，求∠1的度数． （2）如图2，若∠MNC=140°，求∠1的度数．1图150°GBCDEFMNA1ANM FEDCBG50°图225．（12分）如图，一个用铝合金材料加工的长方形窗框，它的宽和高分别为a厘米，b厘米，解答下列问题（结果可用含a，b的代数式表示）．（1）长方形窗框的面积是厘米2；（2）铝合金窗分为上、下两栏，四周框架和中间隔栏的材料均为宽度6厘米的铝合金材料，上栏和下栏的框内高度（不含铝合金部分）的比为1：2（接口用料忽略不计）.①求制作一个该种窗框所需铝合金材料的总长度；②求该种窗框的透光部分的面积.26．（12分）如图，数轴上有三个点A 、B 、C ，它们可以沿着数轴左右移动，请回答：（1）将点B 向右移动三个单位长度后到达点D ，点D 表示的数是 ; （2）移动点A 到达点E ，使B 、C 、E 三点的其中任意一点为连接另外两点之间线段的中点，请你直接写出所有点A 移动的距离和方向；（3）若A 、B 、C 三个点移动后得到三个互不相等的有理数，它们既可以表示为1，a ，b a 的形式，又可以表示为0，b ，ba的形式，试求a ，b 的值.A四、附加题（共10分）友情提示：请同学们做完上面考题后，再认真检查一遍，估计一下你的得分情况．如果你全卷得分低于90分(及格线)，则本题的得分将计入全卷总分，但计入后全卷总分最多不超过90分；如果你全卷得分已经达到或超过90分，则本题的得分不计入全卷总分． 填空：1．计算：（－2）×3＝ .2．已知1=x ，求代数式23+x 的值．永春县2019年秋季七年级期末检测数学科参考答案一．选择题（单项选择，每小题3分，共21分）1.A ；2. D ；3. C ；4.B ；5.B ；6.C ；7.A.二．填空题（每小题4分，共40分）8. 2； 9.1.5×108 ；10.43+a . 11.<； 12. 32423-++x x x ；13. 40；14. -2； 15.41； 16. 2；44； 17. 8, 64. 三、解答题（共89分）18．计算（每小题6分，共12分） (1) -4 (2) -1319．计算（每小题6分，共12分）(1) 222++x x （2） xy 4分 6 6分 20．每小题4分，共8分21．200人 2分 补充条形图 6分 54° 8分 22．每空格2分，共8分23．120千克可包装甲产品300袋，获得的利润300元； 2分 120千克可包装乙产品400袋，获得的利润280元； 4分 120千克可包装丙产品600袋，获得的利润360元； 6分∴丙包装的土特产获得的利润最大，7分 最大利润是360元 8分 24．（1）∵∠EMB=50° ∴∠BMF=180°-50°=130° 1分∵MG 平分∠BMF ∴∠BMG=∠GMN =65° 3分∵AB ∥CD ∴∠1=∠BMG=65° 5分 （2）∵∠MNC=140° ∴∠MNG=40° 7分∠GMN =65° ∴∠1=75° 9分25．（1）ab 3分 （2）上栏框内高度318-b 厘米 下栏框内高度3)18(2-b 厘米 5分 总长度)12(32-+a b +3)18(2-b 8分=（48383-+b a ）厘米 9分（3）透光部分的面积=ab -6（48383-+b a ） 11分 =（2881618+--b a ab ）厘米212分26．（1） 1 2分（2）① 向左移动3个单位长度 4分② 向右移动4.5 单位长度 6分 ③ 向右移动12个单位长度； 8分（3）依题意得：a ≠0，a ≠b ，显然有b =1 9分a +b =0， 10分 a =ba， 11分 解得a =－1，b =1的值. 12分草 稿。

2019年泉州永春初一下第一次抽考数学试卷含解析解析2018-2016学年福建省泉州市永春七年级〔下〕第一次月考数学试卷一、选择题〔每题3分，10小题，共30分〕1、以下各组角中，∠1与∠2是对顶角的为〔〕A、 B、C、D、2、国家提倡“低碳减排”，湛江某公司计划在海边建风能发电站，电站年均发电量约为213000000度，假设将数据213000000用科学记数法表示为〔〕A、213×106B、21、3×107C、2、13×108D、2、13×1093、在实数0，1，，0、1235中，无理数的个数为〔〕A、0个B、1个C、2个D、3个4、如图，∠1=70°，如果CD∥BE，那么∠B的度数为〔〕A、70°B、100°C、110°D、120°5、如图，假设△DEF是由△ABC经过平移后得到的，那么平移的距离是〔〕A、线段BC的长度B、线段BE的长度C、线段EC的长度D、线段EF的长度6、在下述的四个说法中：〔1〕﹣27的立方根是3；〔2〕49的算术平方根为±7；〔3〕的立方根为；〔4〕的平方根为、正确的说法的个数是〔〕A、1B、2C、3D、47、如图，在数轴上表示实数的点可能是〔〕A、点PB、点QC、点MD、点NA、垂线最短B、两直线相交，邻补角相等C、相等的角一定是对顶角D、在同一平面内，过一点有且只有一条直线与直线垂直9、两个角的两边分别平行，其中一个角是60°，那么另一个角是〔〕A、60°B、120°C、60°或120°D、无法确定10、如图，以下条件①∠1=∠2；②∠3=∠4；③∠3+∠4=180°；④∠1+∠2=180°；⑤∠1+∠2=90°；⑥∠3+∠4=90°；⑦∠1=∠4中，能判断直线l1∥l2的条件有〔〕A、②④B、①②⑦C、③④D、②③⑥二、填空题〔每题2分，8小题，共16分〕11、4的平方根是、12、假设ax+1b与ba2的和是一个单项式，那么x= 、13、假设+〔n+1〕2=0，那么m+n的值为、14、= 、15、如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是、16、如图，直线l与a，b相交，请添加一个条件，使a∥b〔填一个你认为正确的条件即可〕17、将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，那么∠1的度数为度、18、如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°、甲、乙两地间同时开工，假设干天后，公路准确接通，那么乙地所修公路的走向是南偏西度、三、计算题〔每题6分，3小题，共18分〕19、计算：〔﹣1〕2+〔﹣2〕3×﹣×〔〕20、先化简，再求值：2x2﹣[7x﹣〔4x﹣3〕+2x2]；其中x=2、21、解方程：﹣=2、四、作图题〔6分〕22、在正方形网格中，每个小正方形的边长均为1个单位长度，三角形ABC的三个顶点的位置如下图，现将三角形ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点、〔1〕请画出平移后的三角形A′B′C′；〔2〕连接AA′，CC′；〔3〕AA′与CC′的位置关系是，数量关系是、五、解答题〔共30分〕23、阅读下面解答过程，并填空或填理由、如下图，点E、F分别是AB和CD上的点，DE、AF分别交BC于点G、H，∠A=∠D，∠1=∠2、试说明：∠B=∠C、解：∵∠1=∠2〔〕∠2=∠3〔〕∴∠3=∠1〔等量代换〕∴AF∥DE〔〕∴∠4=∠D〔〕又∵∠A=∠D〔〕∴∠A=∠4〔等量代换〕∴AB∥CD〔〕∴∠B=∠C〔〕、24、如图，直线AB和CD相交于O点，OE⊥CD，∠EOF=122°，OD平分∠BOF，求∠AOF的度数、25、如图，AB∥CD，∠B=50°，CM是∠BCD的平分线，CM⊥CN，求∠ECN的度数、26、〔1〕如图〔1〕，AB∥CD，点P在AB、CD外部，假设∠B=40°，∠D=15°，那么∠BPD= 、〔2〕如图〔2〕，AB∥CD，点P在AB、CD内部，那么∠B，∠BPD，∠D之间有何数量关系？证明你的结论；〔3〕在图〔2〕中，将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M，如图〔3〕，假设∠BPD=90°，∠BMD=40°，求∠B+∠D的度数、2018-2016学年福建省泉州市永春七中七年级〔下〕第一次月考数学试卷参考答案与试题解析一、选择题〔每题3分，10小题，共30分〕1、以下各组角中，∠1与∠2是对顶角的为〔〕A、 B、C、D、【考点】对顶角、邻补角、【分析】根据对顶角的定义进行判断：两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做对顶角、【解答】解：根据两条直线相交，才能构成对顶角进行判断，A、B、C都不是由两条直线相交构成的图形，错误；D是由两条直线相交构成的图形，正确、应选D、【点评】此题考查对顶角的概念，一定要紧扣概念中的关键词语，如：两条直线相交，有一个公共顶点、反向延长线等、2、国家提倡“低碳减排”，湛江某公司计划在海边建风能发电站，电站年均发电量约为213000000度，假设将数据213000000用科学记数法表示为〔〕A、213×106B、21、3×107C、2、13×108D、2、13×109【考点】科学记数法—表示较大的数、【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数、确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同、当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数、【解答】解：将213000000用科学记数法表示为2、13×108、应选C、【点评】此题考查科学记数法的表示方法、科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值、3、在实数0，1，，0、1235中，无理数的个数为〔〕A、0个B、1个C、2个D、3个【考点】无理数、【分析】无理数就是无限不循环小数、初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0、1010010001…，等有这样规律的数，由此即可判定选择项、【解答】解：在实数0，1，，0、1235中，无理数的是：、应选B、【点评】此题主要考查了无理数的定义、无限不循环小数是无理数、4、如图，∠1=70°，如果CD∥BE，那么∠B的度数为〔〕A、70°B、100°C、110°D、120°【考点】平行线的性质；对顶角、邻补角、【专题】计算题、【分析】先求出∠1的对顶角，再根据两直线平行，同旁内角互补即可求出、【解答】解：如图，∵∠1=70°，∴∠2=∠1=70°，∵CD∥BE，∴∠B=180°﹣∠1=180°﹣70°=110°、应选：C、【点评】此题利用对顶角相等和平行线的性质，需要熟练掌握、5、如图，假设△DEF是由△ABC经过平移后得到的，那么平移的距离是〔〕A、线段BC的长度B、线段BE的长度C、线段EC的长度D、线段EF的长度【考点】平移的性质、【分析】根据平移的性质，结合图形可直接求解、【解答】解：观察图形可知：△DEF是由△ABC沿BC向右移动BE的长度后得到的，∴平移距离就是线段BE的长度、应选B、【点评】此题利用了平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等、6、在下述的四个说法中：〔1〕﹣27的立方根是3；〔2〕49的算术平方根为±7；〔3〕的立方根为；〔4〕的平方根为、正确的说法的个数是〔〕A、1B、2C、3D、4【考点】立方根；平方根；算术平方根、【专题】推理填空题、【分析】分别求出﹣27的立方根是﹣3，49的算术平方根为+7，的立方根为，的平方根为±，根据求出的结果判断即可、【解答】解：∵﹣27的立方根是﹣3，∴〔1〕错误；∵49的算术平方根为+7，∴〔2〕错误；∵的立方根为，∴〔3〕正确；∵的平方根为±，∴〔4〕错误；∴正确的说法的个数是1个，应选A、【点评】此题考查了平方根、立方根、算术平方根的应用，题目具有一定的代表性，但是一道比较容易出错的题目、7、如图，在数轴上表示实数的点可能是〔〕A、点PB、点QC、点MD、点N【考点】估算无理数的大小；实数与数轴、【分析】先对进行估算，再确定是在哪两个相邻的整数之间，然后确定对应的点即可解决问题、【解答】解：∵≈3、87，∴3＜＜4，∴对应的点是M、应选C【点评】此题考查实数与数轴上的点的对应关系，应先看这个无理数在哪两个有理数之间，进而求解、A、垂线最短B、两直线相交，邻补角相等C、相等的角一定是对顶角D、在同一平面内，过一点有且只有一条直线与直线垂直C、∵对顶角一定相等，但相等的角不一定都是对顶角，∴相等的角一定是对顶角不正确，应选D、各知识点段选项进行判定即可、9、两个角的两边分别平行，其中一个角是60°，那么另一个角是〔〕A、60°B、120°C、60°或120°D、无法确定【考点】平行线的性质、【专题】分类讨论、【分析】根据题意分两种情况画出图形，再根据平行线的性质解答、【解答】解：如图〔1〕，∵AB∥DE，∴∠A=∠1=60°，∵AC∥EF，∴∠E=∠1，∴∠A=∠E=60°、如图〔2〕，∵AC∥EF，∴∠A=∠1=60°，∵DE∥AB，∴∠E+∠1=180°，∴∠A+∠E=180°，∴∠E=180°﹣∠A=180°﹣60°=120°、故一个角是60°，那么另一个角是60°或120°、应选C、【点评】此题考查的是平行线的性质，解答此题的关键是要分两种情况讨论，不要漏解、10、如图，以下条件①∠1=∠2；②∠3=∠4；③∠3+∠4=180°；④∠1+∠2=180°；⑤∠1+∠2=90°；⑥∠3+∠4=90°；⑦∠1=∠4中，能判断直线l1∥l2的条件有〔〕A、②④B、①②⑦C、③④D、②③⑥【考点】平行线的判定、【分析】欲判定l1∥l2，需考虑内错角、同旁内角、同位角，从图中可以看出：∠1的补角〔180°﹣∠1〕和∠2且∠3的补角〔180°﹣∠3〕和∠4对于直线l1和l2来说是两对同位角，根据同为角相等，两直线平行可以证明l1∥l2、【解答】解：由图可以看出：∠1的补角〔180°﹣∠1〕和∠2且∠3的补角〔180°﹣∠3〕和∠4对于直线l1和l2来说是两对内错角、假设使180°﹣∠1=∠2，即：∠1+∠2=180°；180°﹣∠3=∠4，即：∠3+∠4=180°；所以，l1∥l2〔同位角相等，两直线平行〕、应选：C、【点评】解答此类要判定两直线平行的题，可围绕截线找同位角、内错角和同旁内角、此题是一道探索性条件开放性题目，能有效地培养“执果索因”的思维方式与能力、二、填空题〔每题2分，8小题，共16分〕11、4的平方根是±2、【考点】平方根、【专题】计算题、【分析】根据平方根的定义，求数a的平方根，也就是求一个数x，使得x2=a，那么x就是a的平方根，由此即可解决问题、【解答】解：∵〔±2〕2=4，∴4的平方根是±2、故答案为：±2、【点评】此题考查了平方根的定义、注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根、12、假设ax+1b与ba2的和是一个单项式，那么x=1、【考点】同类项、【分析】ax+1b与ba2的和是一个单项式，那么它们是同类项，由同类项的定义可求得x的值、【解答】解：由同类项的定义可知x+1=2，得x=1、【点评】同类项定义中的两个“相同”：所含字母相同，相同字母的指数相同，是易混点，因此成了中考的常考点、13、假设+〔n+1〕2=0，那么m+n的值为2、【考点】非负数的性质：算术平方根；非负数的性质：偶次方、【分析】首先根据非负数的性质列出关于m、n方程组，解方程组即可求出n、m的值，代入m+n进行计算即可、【解答】解：∵+〔n+1〕2=0，∴，解得m=3，n=﹣1，∴m+n=3+〔﹣1〕=2、故答案为：2、【点评】此题考查了非负数的性质、初中阶段有三种类型的非负数：〔1〕绝对值；〔2〕偶次方；〔3〕二次根式〔算术平方根〕、当它们相加和为0时，必须满足其中的每一项都等于0、根据这个结论可以求解这类题目、14、=3﹣、【考点】实数的性质、【分析】根据负数的绝对值等于它的相反数解答、【解答】解：|﹣3|=3﹣、故答案为：3﹣、【点评】此题考查了实数的性质，主要利用了绝对值的性质、15、如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是连接直线外一点与直线上所有点的连线中，垂线段最短、【考点】垂线段最短、【专题】应用题、【分析】过直线外一点作直线的垂线，这一点与垂足之间的线段就是垂线段，且垂线段最短、【解答】解：根据垂线段定理，连接直线外一点与直线上所有点的连线中，垂线段最短，∴沿AB开渠，能使所开的渠道最短、故答案为：连接直线外一点与直线上所有点的连线中，垂线段最短、【点评】此题是垂线段最短在实际生活中的应用，表达了数学的实际运用价值、16、如图，直线l与a，b相交，请添加一个条件∠2=∠3，使a∥b〔填一个你认为正确的条件即可〕【考点】平行线的判定、【专题】开放型、【分析】由根据平行线的判定，内错角相等，两直线平行，∠2和∠3是内错角，假设相等，那么a∥B、【解答】解：∵∠2=∠3〔内错角〕∴a∥b〔内错角相等，两直线平行〕、故答案为：∠2=∠3、【点评】此题考查了学生对平行线的判定的理解与掌握、关键是找出内错角或同位角，使它们相等、17、将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，那么∠1的度数为75度、【考点】三角形内角和定理；平行线的性质、【专题】计算题、【分析】根据三角形三内角之和等于180°求解、【解答】解：如图、∵∠3=60°，∠4=45°，∴∠1=∠5=180°﹣∠3﹣∠4=75°、故答案为：75、【点评】考查三角形内角之和等于180°、18、如图，在甲、乙两地之间修一条笔直的公路，从甲地测得公路的走向是北偏东48°、甲、乙两地间同时开工，假设干天后，公路准确接通，那么乙地所修公路的走向是南偏西48度、【考点】方向角；平行线的性质、【专题】应用题、【分析】先根据题意画出图形，利用平行线的性质解答即可、【解答】解：如图，∵AC∥BD，∠1=48°，∴∠2=∠1=48°，根据方向角的概念可知，乙地所修公路的走向是南偏西48°、故答案为：48、【点评】解答此类题需要从运动的角度，正确画出方位角，再结合平行线的性质求解、三、计算题〔每题6分，3小题，共18分〕19、计算：〔﹣1〕2+〔﹣2〕3×﹣×〔〕【考点】实数的运算；有理数的乘方；立方根；二次根式的性质与化简、【分析】此题涉及数的乘方、立方根、二次根式化简3个考点、在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法那么求得计算结果、【解答】解：原式=1﹣8×﹣3×=1﹣1﹣1=﹣1、【点评】此题考查实数的综合运算能力，是各地中考题中常见的计算题型、解决此类题目的关键是熟练掌握数的乘方、立方根、二次根式等考点的运算、20、先化简，再求值：2x2﹣[7x﹣〔4x﹣3〕+2x2]；其中x=2、【考点】整式的加减—化简求值、【专题】计算题；整式、【分析】原式去括号合并得到最简结果，把x的值代入计算即可求出值、【解答】解：原式=2x2﹣7x+4x﹣3﹣2x2=﹣3x﹣3，当x=2时，原式=﹣6﹣3=﹣9、【点评】此题考查了整式的加减﹣化简求值，熟练掌握运算法那么是解此题的关键、21、解方程：﹣=2、【考点】解一元一次方程、【分析】先去分母，然后移项、合并同类项；最后化未知数的系数为1、【解答】解：去分母得：2〔x+2〕﹣〔1﹣x〕=12去括号得：2x+4﹣1+x=12，移项、合并同类项，得3x=9，化未知数x系数为1得：x=3、【点评】此题考查解一元一次方程的解法；解一元一次方程常见的过程有去括号、移项、系数化为1等、四、作图题〔6分〕22、在正方形网格中，每个小正方形的边长均为1个单位长度，三角形ABC的三个顶点的位置如下图，现将三角形ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点、〔1〕请画出平移后的三角形A′B′C′；〔2〕连接AA′，CC′；〔3〕AA′与CC′的位置关系是平行，数量关系是相等、【考点】作图-平移变换、【专题】作图题、【分析】〔1〕由于点向左平移5个单位，再向下2个单位得到点A′，即△ABC向左平移5个单位，再向下2个单位得到△A′B′C′，然后利用此平移规律画出点B′和C′；〔2〕连结AA′，CC′；〔3〕利用平移的性质求解、【解答】解：〔1〕如图，△A′B′C′为所作；〔2〕如图，′′〔3〕AA′与CC′的位置关系是平行，数量关系是相等、故答案为平行，相等、【点评】此题考查了作图﹣平移变换：确定平移后图形的基本要素有两个：平移方向、平移距离、作图时要先找到图形的关键点，分别把这几个关键点按照平移的方向和距离确定对应点后，再顺次连接对应点即可得到平移后的图形、五、解答题〔共30分〕23、阅读下面解答过程，并填空或填理由、如下图，点E、F分别是AB和CD上的点，DE、AF分别交BC于点G、H，∠A=∠D，∠1=∠2、试说明：∠B=∠C、解：∵∠1=∠2〔〕∠2=∠3〔对顶角相等〕∴∠3=∠1〔等量代换〕∴AF∥DE〔同位角相等，两直线平行〕∴∠4=∠D〔两直线平行，同位角相等〕又∵∠A=∠D〔〕∴∠A=∠4〔等量代换〕∴AB∥CD〔内错角相等，两直线平行〕∴∠B=∠C〔两直线平行，内错角相等〕、【考点】平行线的判定与性质、【专题】推理填空题、【分析】根据对顶角的性质填第一个空，根据平行线的判定填第二和第四个空，根据平行线的性质填第三和第五个空、【解答】解：∵∠1=∠2〔〕∠2=∠3〔对顶角相等〕∴∠3=∠1〔等量代换〕∴AF∥DE〔同位角相等，两直线平行〕∴∠4=∠D〔两直线平行，同位角相等〕又∵∠A=∠D〔〕∴∠A=∠4〔等量代换〕∴AB∥CD〔内错角相等，两直线平行〕∴∠B=∠C〔两直线平行，内错角相等〕、【点评】此题只需要根据对顶角的性质和两直线平行的判定方法及性质填写对应的空即可、24、如图，直线AB和CD相交于O点，OE⊥CD，∠EOF=122°，OD平分∠BOF，求∠AOF 的度数、【考点】垂线；对顶角、邻补角、【分析】根据垂直，可得∠DOE的度数，根据角的和差，可得∠FOD的度数，根据角平分线，可得∠BOF的度数，根据∠BOF与∠AOF是邻补角，可得答案、【解答】解：OE⊥CD，∴∠EOD=90°，、∵∠EOF=122°，∴∠DOF=122°﹣90°=32°、∵OD平分∠BOF，∴∠BOF=2∠DOF=64°，∵∠AOF+∠∠BOF=180°，∴∠AOF=180°﹣∠BOF=180°﹣64°=116°、【点评】此题考查了垂线，先求出∠DOF，再求出∠BOF，最后求出答案、25、如图，AB∥CD，∠B=50°，CM是∠BCD的平分线，CM⊥CN，求∠ECN的度数、【考点】平行线的性质、【分析】根据平行线性质求出∠BCD，根据角平分线定义求出∠DCM，求出∠NCM，根据邻补角即可求出答案、【解答】解：∵AB∥CD，∠B=50°，∴∠BCD=∠B=50°，∵CM平分∠BCD，∴∠MCD=∠BCD=25°，∵CM⊥CN，∴∠MCN=90°，∴∠ECN=180°﹣90°﹣25°=65°、【点评】此题考查了对平行线性质和角平分线定义的应用，注意：两直线平行，内错角相等、26、〔1〕如图〔1〕，AB∥CD，点P在AB、CD外部，假设∠B=40°，∠D=15°，那么∠BPD=25°、〔2〕如图〔2〕，AB∥CD，点P在AB、CD内部，那么∠B，∠BPD，∠D之间有何数量关系？证明你的结论；〔3〕在图〔2〕中，将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M，如图〔3〕，假设∠BPD=90°，∠BMD=40°，求∠B+∠D的度数、【考点】平行线的性质；三角形内角和定理、【分析】〔1〕由AB∥CD，∠B=40°，根据两直线平行，内错角相等，即可求得∠BOD 的度数，又由三角形外角的性质，可求得∠BPD的度数；〔2〕首先过点P作PE∥AB，由AB∥CD，可得AB∥PE∥CD，然后由两直线平行，内错角相等，即可证得∠BPD=∠1+∠2=∠B+∠D；〔3〕首先延长BP交CD于点E，利用三角形外角的性质，即可求得∠B+∠D的度数、【解答】解：〔1〕∵AB∥CD，∠B=40°，∴∠BOD=∠B=40°，∴∠P=∠BOD﹣∠D=40°﹣15°=25°、故答案为：25°；〔2〕∠BPD=∠B+∠D、证明：过点P作PE∥AB，∵AB∥CD，∴AB∥PE∥CD，∴∠1=∠B，∠2=∠D，∴∠BPD=∠1+∠2=∠B+∠D；〔3〕延长BP交CD于点E，∵∠1=∠BMD+∠B，∠BPD=∠1+∠D，∴∠BPD=∠BMD+∠B+∠D，∵∠BPD=90°，∠BMD=40°，∴∠B+∠D=∠BPD﹣∠BMD=90°﹣40°=50°、【点评】此题考查了平行线的性质与三角形外角的性质、此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用、X；星期八；py168；zhehe；。

永春一中初一年期末考试数学科参考答案（2019.07）一、选择题（40分）:1.D2.C3.C4. D5.A6.C7. A8.A9.B 10.D二、填空题（24分）：11. 4-3x； 12.47°； 13.x=2,y=1 ； 14. a＜2 ； 15.8/5 16.(1)50°（2）70°三、解答题(86分)：17.（8分）解：移项 .....................3分合并得：， ......................6分解得：； ......................8分18．（8分）解：32255x yx y-=⎧⎨-=⎩①②（如用代入法解可参照本评分标准，直接写答案2分）①×2，得264x y-=③…………………………………………2分③－②，得1y-=-…………………………………………………3分即1y=………………………………………………………4分将1y=代入①，得：32x-=……………………………………5分解得5x=………………………………………………………6分∴51xy=⎧⎨=⎩．……………………………………………………………8分19．（本题8分）解：解不等式①，得x＞3-，………………………………………………………… 2分解不等式②，得x≤1，………………………….……………………………… 4分解不等式①②的解集在数轴上表示如下：…………………… 6分∴不等式组的解集为3-＜x≤1. …………………………………8分20．（本题8分）解：（1）40；………………………………………… 3分（2）∵△AED是由△ABD折叠得到的∴∠AED=∠B=50°，……………… 4分∵∠AED是△AEC的外角，∴∠AED=∠CAE+∠C，………… 6分∴∠CAE=∠AED－∠C=50°－30°=20°. … 8分21．（本题8分）证明：如图BC∥DF∴∠ABC=∠FDE，…………2分在△ABC和△FDE中，，…………6分∴△ABC≌△FDE，…………7分∴AC=EF．…………8分22. （本小题10分）解：如图所示：（1）即为所求．………………2分（2）连接与直线DE的交点P即为所求．………………6分（3）作点C关于直线DE的对称点，连接，交直线DE于点Q，点Q即为所求．…10分23．（本题10分）解：（1）解方程组得：，…………2分解不等式组，解得：﹣4≤x＜11，∵满足﹣4≤x＜11的最大正整数为10，……………………4分∴c=10，∴a=8，b=6，c=10；………………………………5分（2）∵AE平分△ABC的周长，△ABC的周长为24，∴AB+BE=×24=12，∴EC=6，BE=2，∴AC=CE=6，∴△AEC 为等腰直角三角形，∴∠AEC=45°，∠BEA=135°； ……………………10分24.(12分)解：（1）设甲型车每辆装满时可装x 箱药品．则乙型车每辆装满时可装(x+10)箱药品，依题意得x 20320-＝1030320++x解得x ＝60．∴x+10=70(箱)．故甲、乙两型车每辆装满时，各能装60箱，70箱药品．……………………6分(2) 由题意，有W=320a+350b ，且60a+70b ≥320，其中“a ，b ”为非负整数，且0≤a ≤6，经比较发现，当且仅当a ＝3，b ＝2时，药品刚好装完且运输总成本最低，其值为W ＝320×3+350×2＝1 660(元)．……………………12分25.（本题14分）（1）∵∠BA C ＝90°∴AB 2＋AC 2＝BC 2AB ＝8 BC ＝10∴AC ＝6……………………3分(2)如图将△AEC 绕点A 顺时针旋转90°得到△ABM∴△AE C ≌△AMB∴BM ＝EC AM ＝AE ∠C ＝∠ABM ∠EA C ＝∠MAB在RT △ABC 中 AB=AC∠ABC ＝∠ACB ＝45°∴∠AB C ＋∠ABM ＝90°即∠MBD ＝90°∴MB 2＋BD 2＝M D 2又∠DAE ＝45°∴∠BAD ＋∠EAC ＝45°∴∠MAB ＋∠BAD ＝45°即△AM D ≌△AED∴DE ＝DMDE 2 ＝BD 2＋EC 2………………7分(3) 关系式DE 2 ＝BD 2＋EC 2仍然成立证明：将△ADB 沿直线AD 对折，得△AFD ，连接FE ，∴AF=AB，FD=DB，∠FAD=∠BAD，∠AFD=∠ABD，又∵AB=AC，∴AF=AC，∵∠FAE=∠FAD+∠DAE=∠FAD+45°，∠EAC=∠BAC-∠BAE=90°-（∠DAE-∠DAB）=45°+∠DAB，∴∠FAE=∠EAC，又∵AE=AE，∴△AFE≌△ACE，∴FE=EC，∠AFE=∠ACE=45°，∠AFD=∠ABD=180°-∠ABC=135°，∴∠DFE=∠AFD-∠AFE=135°-45°=90°，∴在Rt△DFE中，DF2 +FE2 =DE2，即DE2=BD2 +EC2……………………12分．又如图当动点D在线段BC上，动点E运动到BC的延长线上仍有DE2=BD2 +EC2……………………14分．B。

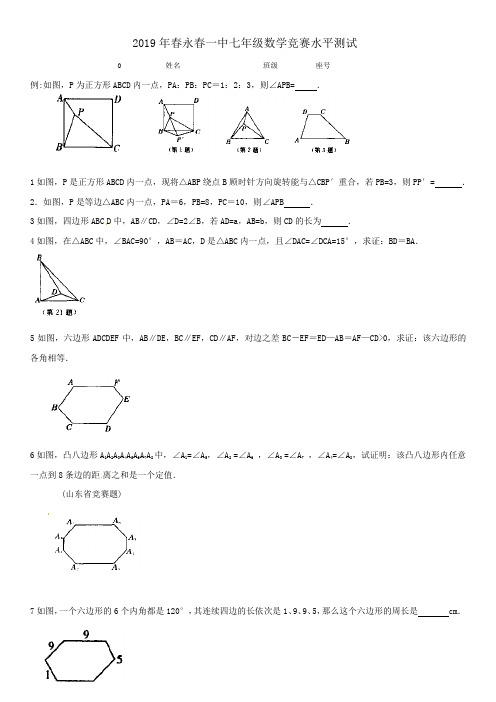
2019年春永春一中七年级数学竞赛水平测试0姓名班级座号例:如图，P为正方形ABCD内一点，PA：PB：PC＝1：2：3，则∠APB= ．1如图，P是正方形ABCD内一点，现将△ABP绕点B顾时针方向旋转能与△CBP′重合，若PB=3，则PP′= ．2．如图，P是等边△ABC内一点，PA＝6，PB=8，PC＝10，则∠APB ．3如图，四边形ABC D中，AB∥CD，∠D=2∠B，若AD=a，AB=b，则CD的长为．4如图，在△ABC中，∠BAC=90°，AB＝AC，D是△ABC内一点，且∠DAC=∠DCA=15°，求证：BD＝BA．5如图，六边形ADCDEF中，AB∥DE，BC∥EF，CD∥AF，对边之差BC－EF＝ED—AB＝AF—CD>0，求证：该六边形的各角相等．6如图，凸八边形A l A2A3A4A5A6A7A8中，∠A l=∠A5，∠A2=∠A6，∠A3=∠A7，∠A4=∠A8，试证明：该凸八边形内任意一点到8条边的距离之和是一个定值．(山东省竞赛题)7如图，一个六边形的6个内角都是120°，其连续四边的长依次是1、9、9、5，那么这个六边形的周长是 cm．8如图，在五边形ABCDE中，∠B＝∠E，∠C=∠D，BC=DE，M为CD中点，求证：AM⊥CD． (武汉市选拔赛试题)9如图，在等腰△ABC的两腰AB、AC上分别取点E和F，使AE=CF．已知BC=2，求证：EF≥1． (西安市竞赛题)10．如图，已知△ABC中，AB=AC，D为AB上一点，E为AC 延长线上一点，BD=CE，连DE，求证：DE>DC．11（1）如图，四边形ABCD中，AB=AD，∠ABD=60°，∠BCD=120°，证明：BC+DC=AC．(1)如图，四边形ABCD中，AB=BC，∠ABC=60°，P为四边形ABCD内一点，且∠APD=120°，证明：PA+PD+PC≥BD． (江苏省竞赛题)。

七年级数学竞赛试题精选1. 计算(-1-2-3-4-5-6-7-8-9-10)×(1-2+3-4+5-6+7-8+9-10)=___________。

2. 计算:3. 已知：4. 若5. 三个连续自然数的最小公倍数为660，则这三个数分别是_______。

6. 关于x的不等式 (2a-b)x+a-5b＞0的解为,那么关于x的不等式ax＞b的解为____。

7. 满足不等式的所有整数解的和为______。

8. 若-1＜a＜0,则在下列的(A)、（B）、（C）、（D）四个不等式中，有___个不等式是正确的,它们是_____。

9. 已知a＞b＞0,m＜0,用不等号或等号连接下式:。

10. 有两组数, 第一组的平均数为12.8, 第二组数的平均数为10.2, 这两组数的总平均数为12.02,那么,第一组数的个数与第二组数的个数的比值为______。

11. 如图1,BMDF和ADEN都是正方形,已知△CDE的面积为6,则△ABC的面积为____。

12. 一个三位数,个位数字是十位数字的平方,百位数字是十位数的4倍还多1,那么符合条件的三位数中最大为_____,最小为______。

13. 如图2,长方形ABCD中,E是CD中点,则图中形状和大小都相同的三角形共有____对。

14. 甲、乙、丙、丁四位老师分别教数学、物理、化学、英语，甲老师可以教物理、化学；乙老师可以教数学、英语；丙老师可以教数学、物理、化学；丁老师只能教化学，为了使每人都能胜任工作，那么教数学的是_______老师。

15. 规定"*"为一种运算,它满足a*b=那么,1992*(1992*1992)=____。

16. 图中的□、△、○各代表一个数字，且满足以下三个等式：□+□+△+○=17□+△+△+○=14□+△+○+○=13则□代表的数字是______。

17. 若a、b、c是自然数，且a＜b，a+b=719，c-a=915，则a+b+c的所有可能值中最大的一个是______。

福建省七年级下学期数学竞赛试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分）如图，若点A是实数a在数轴上对应的点，则关于a，－a，1的大小关系表示正确的是（）．A . a＜1＜－aB . a＜－a＜1C . 1＜－a＜aD . －a＜a＜12. （2分） (2020七上·醴陵期末) 下列运用等式性质进行的变形，正确的是（）A . 如果a＝b，那么a+c＝b﹣cB . 如果a2＝3a，那么a＝3C . 如果a＝b，那么D . 如果，那么a＝b3. （2分） (2020七上·宣城月考) 数轴上与表示的点的距离为5个单位的点，表示的有理数是（）A . 7或-3B . -7C . +3D . -7或34. （2分） (2019七上·杭州期末) 一个代数式减去-2x得-2x2-2x+1，则这个代数式为（）A .B .C .D .5. （2分） (2018七上·新洲期中) 设实数a,b,c满足a＞b＞c(ac＜0)，且|c|＜|b|＜|a|，则|x-a|+|x+b|+|x-c|的最小值为（）A .B . |b|C . a+bD . －c－a6. （2分）根据下图中的程序，当输入x=-4时，输出结果y为（）A . －1B . －3C . 3D . 57. （2分） (2020七下·江阴月考) 若△ABC内有一个点P1 ，当P1、A、B、C没有任何三点在同一直线上时，如图1，可构成3个互不重叠的小三角形；若△ABC内有两个点P1、P2 ，其它条件不变，如图2，可构成5个互不重叠的小三角形：……若△ABC内有n个点，其它条件不变，则构成若干个互不重叠的小三角形，这些小三角形的内角和为（）A . n·180°B . （n+2）·180°C . （2n-1）·180°D . （2n+1）·180°8. （2分） (2019七上·江阴期末) 已知a + b =3，b − c = 12，则a + 2b − c的值为（）A . 15B . 9C . −15D . −99. （2分） (2020七上·景县期中) 程序框图的算法思路源于我国古代数学名著《九章算术》，如图所示的程序框图，当输入的值是20时，根据程序计算，第一次输出的结果为10，第二次输出的结果为5……这样下去第2020次输出的结果为（）A . -2B . -1C . -8D . -410. （2分） (2019七上·兴化月考) 将、、、按如下方式排列，若规定表示第排从左向右第个数，表示的数是（）A .B .C . cD .二、填空题 (共9题；共17分)11. （1分） (2018七下·宝安月考) 若实数a满足a3+a2﹣3a+2= ﹣﹣，则a+ =________12. （1分） (2020七上·娄星期末) 如果方程是一个关于x的一元一次方程，那么k的值是________．13. （2分） (2019八上·金平期末) 如图，∠MON＝30°，点A1、A2、A3…在射线ON上，点B1、B2 ，B3…在射线OM上，△A1B1A2 ，△A2B2A3 ，△A3B3A4…均为等边三角形，从左起第1个等边三角形的边长记a1 ，第2个等边三角形的边长记为a2 ，以此类推，若OA1＝3，则a2=________，a2019=________.14. （1分）如图是一个正方体的展开图，在a、b、c处填上一个适当的数，使得正方体相对的面上的两数互为相反数，则的值为________15. （1分）正方形A1B1C1O，A2B2C2C1 ， A3B3C3C2 ，…按如图的方式放置．点A1 ， A2 ， A3 ，…和点C1 ， C2 ， C3 ，…分别在直线y=x+1和x轴上，则点B6的坐标是________．16. （3分）根据题意，列出关于x的方程（不必解方程）：（1）要锻造一个直径为10cm，高为8cm的圆柱体毛坯，应截取直径为8cm的圆钢多长？设应截取直径为8cm 的圆钢x cm，则可列出方程________ ；（2）某人存了一笔三年定期存款，年利率为4.25%，今年到期后，连本带息取出11275元，他三年前存了多少元？设他三年前存了x元，则可列出方程________ ．（3）把2005个正整数1，2，3，4，…，2005按如图方式排列成一个表，用一正方形框在表中任意框住4个数，被框住的4个数之和能否等于416？设正方形框中左上角的一个数为x，则可列出方程________ ．17. （1分） (2021八下·瑶海期中) 如图，一系列等腰直角三角形（编号分别为①，②，③，④，…）组成了一个螺旋形，其中第 1 个三角形的直角边长为 1，则第 n 个等腰直角三角形的面积为________18. （2分） (2017七下·延庆期末) 如图，由等圆组成的一组图中，第1个图由1个圆组成，第2个图由5个圆组成，第3个图由11个圆组成，…，按照这样的规律排列下去，则第9个图形由________个圆组成，第n个图形由________个圆组成．19. （5分）观察下列等式：①；②；③；④；……（1）猜想并写出第个算式：（2）请说明你写出的算式的正确性（3）计算下列式子的值（写出过程）+++…+三、解答题 (共8题；共68分)20. （25分） (2020七上·武进月考) 计算：（1）（﹣6）﹣（+15）+4﹣（﹣15）（2）﹣2×3﹣（﹣4）×2+3（3）（﹣）×（﹣24）（4）﹣14﹣2×（﹣3）2÷（﹣）（5）﹣18÷（﹣3）2+5×（﹣2）3﹣（﹣15）÷521. （5分） (2019七上·开州月考) 用简单方法计算下列各题。

七年级数学竞赛试题精选全卷三大题，19小题。

时间120分钟满分120分题号一二15 16 17 18 19 总分得分一、选择题（每小题后面代号为A，B，C，D的四个选项中，只有一个正确，将他的代号字母填在题后的括号里，选对一题4分，不选和选错0分，本题满分为32分）1、在邮局投寄平信，质量不超过20克，需贴0.8元钱的邮票；超过20克但不超过40克，需贴1.6元钱的邮票；超过40克但不超过60克，需贴2.4元钱的邮票……某顾客的平信重91.2克，他需贴邮票（）A、3.2元B、3.5元C、3.8元D、4元2、在售价不变的情况下，如果把某种商品的进价降低5%，利润可由目前的a%提高到（a+5）%。

（提高15个百分点）那么a是（）A、185B、175C、155D、1453、“保护野生鸟类行动”实施以来，在危水开发区过冬的鸟逐年增多，2001年为x只，2002年比2001年增加了50%，2003年又比2002年增加了一倍。

2003年在危水开发区过冬的鸟的只数为（）A、2xB、3xC、4xD、1.5x4、如图是一个由16个小正方形拼成的大正方形，则∠1+∠2+∠3+…∠16的度数是（）A、8400B、7200C、6750D、63005、已知a= ,b= ,c= 则a、b、c之间的大小关系是（）A、a>b>cB、a>c>bC、b>c>aD、c>b>a6、金海岸船务公司同时每间隔1小时在大连与上海之间发一班船，每班船行经6小时到达对方港。

某人乘坐此船从大连到上海，遇到该公司的船迎面开来的次数是（）（在港口遇到的也算）Ａ、６次Ｂ、７次Ｃ、１２次Ｄ、１３次７、我国股票交易中，每买卖一次需付交易款的7.5‰的交易费，某投资者以每股ｘ元买进“东升毛纺”1000股，每股上涨２元后全部卖出，则以下说法正确的是（）A、盈利2000元B、盈利 1985元C、时可以盈利D、时可以盈利8、一个水池装有5只水管，有些是进水管，有些是出水管，依次编号为①②③④⑤，分别打开两管，注满水池的时间记录如下表：打开水管号①②②③①③②④③⑤注满水池（分钟） 6 8 12 13 15要想单独打开一只水管，用最短的时间注满水池，应打开（）A、①号水管B、②号水管C、③号水管D、④号或⑤号水管二、填空题（每小题5分，共30分）9、猴年贺岁，一群猴了骑着m辆自行车，把一些鲜花抛向空中，有n辆车上有3只猴子，另一些车每辆车上有5只猴子，猴子一共的只数是。

2019永春二中新初一入学数学试卷（满分100分，考试时间：70分钟）一、填空题。

（每小题2分，共18分）1.538 的分数单位是______，再添上_______个这样的分数单位就是10以内最大质数。

2.a ×112 = b ×113 = c ×114 （a 、b 、c 都不为零），那么a 、b 、c 从大到小排列__________。

3.一条公路，已修的长度比未修的长度少21，这时修了这条公路长度的__________%。

4.2019年五月份，阴天比晴天少13 ，雨天比晴天少35 ，这个月有_________天是晴天。

5. 今年小华和小玲的年龄和是22岁，4年前小华8岁，小玲___________岁。

6. 把一根木料锯成4段要6分钟，锯成7段要___________分钟。

7.桌子上并排放着三张扑克牌，A 右边的两张中至少有一张K ，而K 左边的两张中也有一张K ；黑桃左边的两张中至少有一张红桃，而红桃右边的两张中也有一张红桃，中间的那张牌是___________。

8. 一个三角形的三个内角度数的比是1:1:2，这个三角形是___________三角形。

9. 等底等高的圆柱和圆锥的体积之差是40立方米，圆柱的体积是_________立方米。

二、选择题。

（每小题2分，共10分）1.A 、B 、C 、D 、E 五名同学进行象棋比赛，每2人都要赛一场，到现在为止，A 赛了4场，B 赛了3场，C 赛了2场，D 赛了1场，那么E 赛了（ ）场。

A ．2B ．3C ．4D ．52. 今年高考的科目有语文、数学、外语、物理、化学、生物、历史、地理、政治，其中语文、数学、外语三科必考，其余6门中只要选考两科。

一位学生今年参加高考，他将有（ ）种不同的选择。

A ． 6B ． 15C ． 36D ． 72………………………………………………………………………………密封线……………………………………………………………考室考号姓名3. 电影门票30元一张，降价后观众增加1倍，收入增加，则一张门票降价（ ） A ．25元 B ．20元 C ．15元 D ．10元4.某班的男生人数比全班学生人数的59 少4人，女生人数比全班学生人数的40%多6人。