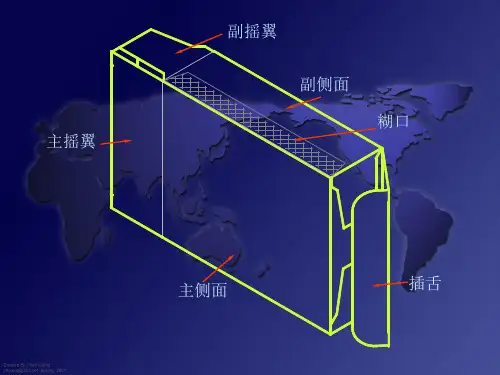
折叠纸盒结构
- 格式:ppt
- 大小:3.43 MB
- 文档页数:14




折叠纸盒的面积计算公式在日常生活中,我们经常会用到纸盒来装载物品,比如礼物、食品、文件等。
而在制作纸盒的过程中,我们需要计算纸盒的面积,以确保纸盒可以容纳所需的物品。
本文将介绍折叠纸盒的面积计算公式,并通过实例演示如何应用这个公式。
首先,我们需要了解折叠纸盒的基本结构。
一般来说,折叠纸盒由六个面构成,分别是底面、顶面和四个侧面。
在计算纸盒的面积时,我们需要分别计算这六个面的面积,然后将它们相加得到总的面积。
底面和顶面的面积计算比较简单,它们通常是一个矩形或正方形的面积。
如果底面和顶面的形状相同,那么它们的面积可以用同一个公式来计算。
假设底面和顶面的长分别为L,宽分别为W,则它们的面积S1可以用以下公式计算:S1 = L W。
接下来,我们需要计算四个侧面的面积。
侧面通常是一个长方形或矩形,其面积可以用长和高来计算。
假设侧面的长为L,高为H,则侧面的面积S2可以用以下公式计算:S2 = 2 L H。
在这里,我们乘以2是因为纸盒有四个侧面,所以我们需要将每个侧面的面积都计算进去。
最后,我们将底面、顶面和侧面的面积相加,就可以得到折叠纸盒的总面积:总面积 = S1 + S1 + 4 S2。
现在,让我们通过一个实例来演示如何应用这个公式。
假设我们要制作一个底面长为10厘米,宽为8厘米,高为5厘米的纸盒。
首先,我们可以计算底面和顶面的面积:底面和顶面的面积 = 10 8 = 80平方厘米。
接下来,我们计算侧面的面积。
侧面的长为10厘米,高为5厘米,所以侧面的面积为:侧面的面积 = 2 10 5 = 100平方厘米。
最后,我们将底面、顶面和侧面的面积相加,就可以得到纸盒的总面积:总面积 = 80 + 80 + 4 100 = 480平方厘米。
通过这个实例,我们可以看到如何应用折叠纸盒的面积计算公式来计算纸盒的总面积。
这个公式可以帮助我们在制作纸盒时准确地计算纸盒的面积,以确保纸盒可以容纳所需的物品。
除了上面介绍的基本情况外,折叠纸盒的面积计算公式还可以根据纸盒的形状和结构进行调整。
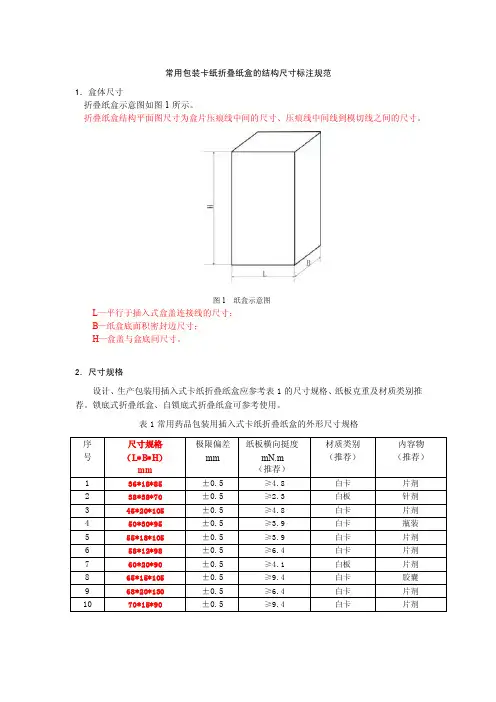
常用包装卡纸折叠纸盒的结构尺寸标注规范
1.盒体尺寸
折叠纸盒示意图如图1所示。
折叠纸盒结构平面图尺寸为盒片压痕线中间的尺寸、压痕线中间线到模切线之间的尺寸。
图1 纸盒示意图
L—平行于插入式盒盖连接线的尺寸;
B—纸盒底面积密封边尺寸;
H—盒盖与盒底间尺寸。
2.尺寸规格
设计、生产包装用插入式卡纸折叠纸盒应参考表1的尺寸规格、纸板克重及材质类别推荐。
锁底式折叠纸盒、自锁底式折叠纸盒可参考使用。
表1常用药品包装用插入式卡纸折叠纸盒的外形尺寸规格。




折叠纸盒结构实验报告1. 实验介绍本实验旨在探究折叠纸盒的结构特点和折叠技巧,并研究不同折叠纸盒结构的稳定性和承重能力。
通过实际操作和测试,通过量化分析折叠纸盒结构的性能,为设计和应用折叠纸盒提供参考。
2. 实验步骤2.1 准备工作准备材料包括:- 彩色卡纸(厚度为0.2mm);- 剪刀和胶水;- 测量尺和直尺。
2.2 设计与制作根据折叠纸盒的结构要求,设计并制作三个不同结构的纸盒样品。
2.2.1 直角折叠纸盒首先,以直角折叠为基础,按照以下步骤制作:1. 按照尺寸要求剪切卡纸为正方形;2. 将卡纸对角线对折,形成两个三角形;3. 将两个三角形的较长边折叠,使其与对角线共线;4. 斜边折叠后,再次对折与对边重合;5. 用胶水粘合纸盒固定。
2.2.2 六面折叠纸盒在直角折叠纸盒的基础上,添加两个边的折叠设计,制作以下结构:1. 按照尺寸要求剪切卡纸为矩形;2. 将矩形折叠成长方体,固定两端;3. 将两个边对折并粘合固定。
2.2.3 双拉链折叠纸盒在六面折叠纸盒的基础上,添加拉链结构设计,制作以下结构:1. 按照尺寸要求剪切卡纸为长方形;2. 将卡纸对折,形成一个矩形;3. 在矩形两边分别绘制拉链结构;4. 将拉链部分逐渐折叠并粘合固定。
3. 实验结果与分析3.1 结构稳定性测试通过在水平面上放置纸盒,观察不同结构纸盒在不同位置的稳定性。
结果显示:双拉链折叠纸盒最稳定,六面折叠纸盒次之,直角折叠纸盒最不稳定。
直角折叠纸盒容易倒塌,受力单一,而双拉链折叠纸盒能够更好地承受压力,结构稳定性较高。
3.2 承重能力测试在水平面上放置纸盒,并逐渐加重,测试纸盒的承重能力。
结果显示:双拉链折叠纸盒的承重能力最高,六面折叠纸盒次之,直角折叠纸盒最低。
直角折叠纸盒的稳定性较差,往往在受到较小的压力时就会塌陷,承重能力有限。
4. 结论折叠纸盒的结构和稳定性密切相关,不同结构纸盒的稳定性和承重能力有所差异。
双拉链折叠纸盒结构稳定性较高,承重能力较强;六面折叠纸盒次之;直角折叠纸盒结构较为简单,稳定性和承重能力较低。

第三节盘式折叠纸盒一、盘式折叠纸盒1、盘式折叠纸盒根据成型特点,盘式折叠纸盒是由一页纸板四周以直角或斜角折叠成主要盒型,有时在角隅处进行锁合或粘合,盒底上几乎无结构变化,主要的结构变化在盒体位置。
适合于包装鞋帽、服装、食品和礼品。
2、盘式折叠纸盒的旋转性成型时角隅相邻的各个盒板围绕一个点进行旋转,这个点就是盒底平面的各个顶点。
A成型角:盘式折叠纸盒盒底相邻两边所构成的角度为A成型角,用α表示。
B成型角:盘式折叠纸盒盒体体板的交线与盒底边线所构成的角度为B成型角,用1γ、2γ……表示。
旋转角:盘式折叠纸盒在平面展开图上,相邻两体板(边板和端板)所构成的角度为旋转角,用β表示。
托盘式瓦楞纸盒,主要用于果蔬包装,其特点是上下层堆码时互相锁口,因而稳定性好。
二、盘式折叠纸盒的成型方式1、组装①盒端对折组装②非粘合式简单盒角与盒端对折组装2、锁合①锁合方式②锁口结构3、粘合式简单盒角三、盘式折叠纸盒的盒盖结构1、罩盖式罩盖式的盒体盒盖是两个独立的盘型结构,盒盖的长度与宽度尺寸比盒体略大一些。
①天罩地式:HH+≥②帽盖式:HH+<③对口盖式:1HHH+=+(其中1H为纸盒全高)2、摇盖式3、插别式4、正揿封口式5、抽屉盖式6、锁口式四、盘式折叠纸盒的平分角设计1、粘合式或非粘合式简单盒角都是在盘式盒的角隅处进行平分角处理。
2、方向转变折叠纸盒的某一部分需要通过对折的角平分线,实现该部分结构方向的转变。
3、盘式自动折叠纸盒成型后可以折叠成平板状,使用时只要张开盒体,纸盒自动恢复成型。
①毕尔斯(Beers)式折叠纸盒分为内折式与外折式两种,不论是肉折式还是外折式,折叠线都将B成型角平分。
②布莱特伍兹(Brightwoods)式折叠纸盒③前向自动折叠纸盒不论向内还是向外平折,如果角隅处的α、1γ、2γ均为90°,则对折线与盒底的角度为45°,即该角为B成型角1γ的平分角。
④TLIC。
第三公式——内折叠角求解公式⑤TLIC第四公式——外折叠角求解公式五、叠纸包装盒第四节管盘式折叠纸盒一、管盘式折叠纸盒传统异型盒,不论是管式或盘式,在其角隅处的任一个旋转点上。
截面形状变化异型管异型结构设计盒体形状变化 封闭端形状变化异型管形结构横截面形状变化三角形管式纸盒需要一个额外的工作线需要一个额外的工作线((伪工作线伪工作线))以使三角形的纸盒坯在送下胶粘机时可以折叠成平板状在送下胶粘机时可以折叠成平板状。
伪工作线在纸盒成型后没有作用后没有作用。
三角形纸盒的第二种选择结构包括第四块面板和一条伪工作线,二者在纸盒成型后都被隐藏。
这种结构比上面所示的要使用更多的纸板,但在美学上更令人感到愉悦。
钻石形管式纸盒是对传统的长方形纸盒作了较小的改动,这里所示的是用简单的折叠插口封闭的这里所示的是用简单的折叠插口封闭的,,也可以使用自动成型方式进行封盒自动成型方式进行封盒。
钻石形管式纸盒这种特定的不对称四边形不需要伪工作线这种特定的不对称四边形不需要伪工作线,,因为一组主体面板体面板((1和2)的长度之和等于另一组的长度之和等于另一组((2和3)的长度之和之和。
不对称四边形形管式纸盒传统的五边形管式纸盒需要一条伪工作线以使纸盒从胶粘机上成型后可以被折成平板状粘机上成型后可以被折成平板状。
五边形形管式纸盒可以制成不带伪工作刻痕的不对称五边形可以制成不带伪工作刻痕的不对称五边形,,只需要三块面板面板((例中的1、2、5)的长度之和等于其余两块面板(3和4)的长度之和的长度之和。
不对称五边形形管式纸盒制作传统的五边形管式纸盒而隐藏所需的伪工作刻痕的方法是加上第六块面板方法是加上第六块面板,,在成型后该面板被折入并藏在其余主体面板中的一块后面其余主体面板中的一块后面。
第六块面板被反向折叠分为面板6a 和6b 。
六块面板的五边形形管式纸盒如图所示如图所示,,六边为相同尺寸六边为相同尺寸,,但六边形常被制作为前后面板的长度比左右侧面板明显增长的形式面板的长度比左右侧面板明显增长的形式((图3),这两种情况下都可以沿传统的拐角刻痕折成平板状种情况下都可以沿传统的拐角刻痕折成平板状。
六边形形管式纸盒图示的七边形管式纸盒不需要伪工作刻痕图示的七边形管式纸盒不需要伪工作刻痕,,因为面板1、5、6、7的组合长度与2、3、4的组合长度相等的组合长度相等。