中考数学题目之三角形分类训练一三角形三边关系鲁教版

鲁教版九年级数学上册《第二章直角三角形的边角关系》单元检测题-附答案学校:___________班级：___________姓名：___________考号：___________一、单选题(共10小题，满分40分)1．如图，某游乐场一滑梯长为l ，滑梯的坡角为α，那么滑梯的高h 的长为（ ）A ．1sin αB ．tan l α⋅C ．cos l α⋅D ．sin l α⋅2．如图，在44⨯的正方形网格中，tan a 的值为（ ）A ．12 B ．2 C 25 D 53．在Rt ABC △中90,12,5C AC BC ∠=︒==，则tan A 的值为（ ）A ．512B ．125C ．1213D ．5134．如图，在RtΔABC 中∠C=90°，AC=6，BC=8，则sin∠A 的值（ ）A ．35B ．45C ．34D ．535．如图，在ABC 中90ACB ∠=︒，26ABC ∠=︒ 6BC =若用科学计算器求边AC 的长，则下列按键顺序正确的是（ ）A ．B ．C ．D ．6．等边ABC 放置在如图所示的平面直角坐标系中，将ABC 绕着点A 逆时针转旋60°到ACD 处，若点B 的坐标为(1,0)-，则点D 的坐标为（ ）A ．(2,2)B ．(3,2)C ．3)D ．3)7．如图所示的衣架可以近似看成一个等腰三角形ABC ，其中AB AC = 37?ABC ∠= 40cm BC =，则高AD 约为（ ）（结果取整数，参考数据：sin370.60︒= cos370.80︒≈ tan370.75︒≈）A ．15cmB ．16cmC ．18cmD ．20cm8．如图，由四个全等的直角三角形围成的大正方形的面积是169，小正方形的面积为49，则cosα＝( )A ．1213B ．512C ．513D ．7129．在综合实践课上，某班同学测量校园内一棵树的高度．如图，测量仪在A 处测得树顶D 的仰角为45°，在C 处测得树顶D 的仰角为37°（点A 、B 、C 在同一条水平主线上），已知测量仪的高度 1.65AE CF ==米，28AC =米，则树BD 的高度是（ ）【参考数据：sin370.60︒≈ cos370.80︒≈ tan370.75︒≈】A ．12米B ．12.65米C ．13米D ．13.65米10．如图，已知点A 是第一象限内横坐标为23AC x ⊥轴于点M ，交直线12y x =-于点N ．若点P 是线段ON 上的一个动点60APB ∠=︒，BA PA ⊥则点P 在线段ON 上运动时，A 点不变，B 点随之运动，求当点P 从点O 运动到点N 时，点B 运动的路径长是（ ）A ．43B ．10C ．210D ．35二、填空题（共8小题，满分32分）11．计算：332(4)(0.25)(sin 601)-⨯-︒-＝ ．12．如图所示，自动扶梯AB 段的长度为20米，倾斜角A 为α，高度BC 为 米．（结果用含α的三角函数表示）13．在如图所示的网格中，小正方形的边长为1，点、、A B C 都在格点上，则tan A 的值是 ．14．如图，Rt ∠ABC 中，∠A =90°，∠B =30°，BC =2，AB = ．15．如图，在四边形 ABCD 中，CA 平分BCD ∠ AB AC ⊥ 60B ∠=︒ AE BC ⊥于点E ．若 10BC =，则点A 到 CD 的距离为 ．16．如图，在平面直角坐标系xOy 中，点A 、D 在第一象限内且点()1,3A a a -，点()1,0C -点()2,0B 45ACD ∠=︒ 点B 到射线CD 的最小值是 ．17．中国古代数学家赵爽在为《周髀算经》作注解时，用4个全等的直角三角形拼成正方形（如图），并用它证明了勾股定理，这个图被称为“赵爽弦图”．作EM NG AD ∥∥，若2GF FM =，则MN FD的值为 ．18．如图，在正方形ABCD 中，边长为2的等边三角形AEF 的顶点E ，F 分别在BC 和CD 上，下列结论：∠CE=CF ；3∠BE+DF=EF ；∠∠AEB=75°．其中正确的序号是 ．三、解答题（共6小题，每题8分，满分48分）19．（1）计算：cos30°－1227－1)0（2）如图，在Rt △ABC 中，∠A=30° ，BC=1，点D ，E 分别是直角边BC ，AC 的中点，求DE 的长．20．（1)2011122tan 603π22-⎛⎫-︒-+- ⎪⎝⎭； （2）先化简，再求值：352242x x x x -⎛⎫÷-- ⎪--⎝⎭，其中33x =． 21．2023年5月30日9点31分，“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射，成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站．如图，在发射的过程中，飞船从地面O 处发射，当飞船到达A 点时，从位于地面C 处的雷达站测得AC 的距离是8km ，仰角为30︒；10s 后飞船到达B 处，此时测得仰角为45︒．求飞船从A 处到B 处的平均速度．（结果精确到0.1km/s 3 1.73≈）22．如图∠、∠分别是某款高压电塔的实物图和示意图．电塔的底座AB 与地面平齐，DF 表示电塔顶端D 到地面的距离，已知AF 长5m ，支架AC 与地面夹角86BAC ∠=︒，顶端支架DC 长10m ，DC 与水平线CE 之间的夹角 45DCE ∠=︒，求电塔的高度DF ． （结果保留整数，参考数据：sin 860.998,cos860.070,tan 862 1.4︒≈︒≈︒≈）23．如图，OABC 的顶点O 与坐标原点重合，边OA 在x 轴正半轴上60AOC ∠=︒，2OC =反比例函数()0k y x x=>的图像经过顶点C ，与边AB 交于点D ．(1)求反比例函数的表达式．(2)尺规作图：作OCB ∠的平分线交x 轴于点E ．（保留作图痕迹，不写作法）(3)在（2）的条件下，连接DE ，若DE CE ⊥，求证：AD AE =． 24．如图，在ABC 中90BAC ∠=︒，AB=3，BC=5，点P 从点B 出发，沿线段BC 以每秒3个单位长度的速度向点C 运动．当点P 不与点B 重合时，作PQ BC ⊥交边AB 于点Q ，当点Q 和点A 重合时，点P 停止运动，以PQ 为直角边向右作等腰Rt PQH △，使90PQH ∠=︒，设点P 的运动时间为t 秒．(1)线段PQ的长为________（用含t的代数式表示）；(2)当点H落在边AC上时，求线段PQ的长；(3)连接CH，当PQH与PHC相似时，求t的值．参考答案1．D2．B3．A4．B5．D6．D7．A8．A9．D10．D11312．20sinα13．3 4143 1553163535 517515 218．∠∠∠19．（13；（2）DE=120．（1）5；（2）126x+321．()0.3km /s 22．36m 23．(1))30y x >(2)(3)略 24．(1)4t ；(2)6037；(3)511．。

2021-2022学年鲁教版九年级数学上册《第2章直角三角形的边角关系》期末综合复习训练1（附答案）1．如图，△ABC的顶点都在正方形网格的格点上，则cos C的值为（）A．B．C．D．2．若0°＜∠A＜45°，那么sin A﹣cos A的值（）A．大于0B．小于0C．等于0D．不能确定3．α为锐角，若sinα+cosα＝，则sinα﹣cosα的值为（）A．B．±C．D．04．若角α，β都是锐角，以下结论：①若α＜β，则sinα＜sinβ；②若α＜β，则cosα＜cosβ；③若α＜β，则tanα＜tanβ；④若α+β＝90°，则sinα＝cosβ．其中正确的是（）A．①②B．①②③C．①③④D．①②③④5．如图，把一块直尺与一块三角板如图放置，若∠2＝135°，则tan∠1的值为（）A．B．C．1D．6．用科学计算器计算锐角α的三角函数值时，不能直接计算出来的三角函数值是（）A．cotαB．tanαC．cosαD．sinα7．如果等腰三角形的周长是底边长的5倍，那么它的顶角的正弦值为（）A．B．C．D．8．如图，为了测量河对岸l1上两棵古树A、B之间的距离，某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点，测得∠ACB＝15°，∠ACD＝45°，若l1、l2之间的距离为50m，则A、B之间的距离为（）A．50m B．25m C．（50﹣）m D．（50﹣25）m9．如图，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为（）A．2m B．2m C．（2﹣2）m D．（2﹣2）m 10．如图，两建筑物的水平距离为a米，从A点测得D点的俯角为α，测得C点的俯角为β，则较低建筑物的高为（）A．a米B．a cotα米C．a cotβ米D．a（tanβ﹣tanα）米11．如图，若点A的坐标为，则sin∠1＝．12．比较大小：cos36°cos37°．13．△ABC中，∠C＝90°，tan A＝，则sin A+cos A＝．14．如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为D．给出下列四个结论：①sinα＝sin B；②sinβ＝sin C；③sin B＝cos C；④sinα＝cosβ．其中正确的结论有．15．在直角△ABC中，AC＝BC，AB＝4，则BC＝．16．如图，在Rt△ABC中，∠C＝90°，M是直角边AC上一点，MN⊥AB于点N，AN＝3，AM＝4，求cos B的值．17．附加题：如图，在Rt△ABC中，BC、AC、AB三边的长分别为a、b、c，则sin A＝，cos A＝，tan A＝．我们不难发现：sin260°+cos260°＝1，…试探求sin A、cos A、tan A 之间存在的一般关系，并说明理由．18．计算：（1）sin260°﹣tan30°•cos30°+tan45°；（2）．19．已知：如图，在Rt△ABC中，∠ACB＝90°，BC＝，cot∠ABC＝，点D是AC 的中点．（1）求线段BD的长；（2）点E在边AB上，且CE＝CB，求△ACE的面积．20．每年的6至8月份是台风多发季节，某次台风来袭时，一棵大树树干AB（假定树干AB 垂直于地面）被刮倾斜15°后折断倒在地上，树的顶部恰好接触到地面D（如图所示），量得树干的倾斜角为∠BAC＝15°，大树被折断部分和地面所成的角∠ADC＝60°，AD ＝4米，求这棵大树AB原来的高度是多少米？（结果精确到个位，参考数据：≈1.4，≈1.7，≈2.4）21．9月23日强台风“天兔”登录深圳，伴随着就是狂风暴雨．梧桐山山坡上有一棵与水平面垂直的大树，台风过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面（如图所示）．已知山坡的坡角∠AEF＝23°，量得树干的倾斜角为∠BAC＝38°，大树被折断部分和坡面所成的角∠ADC＝60°，AD＝3m．（1）求∠DAC的度数；（2）求这棵大树折断前的高度．（结果保留根号）22．我市在城市建设中，要拆除旧烟囱AB（如图所示），在烟囱正西方向的楼CD的顶端C，测得烟囱的顶端A的仰角为45°，底端B的俯角为30°，已量得DB＝21m．（1）在原图上画出点C望点A的仰角和点C望点B的俯角，并分别标出仰角和俯角的大小；（2）拆除时若让烟囱向正东倒下，试问：距离烟囱正东35m远的一棵大树是否被歪倒的烟囱砸着？请说明理由．（≈1.732）23．如图，海中有一小岛P，在距小岛P的海里范围内有暗礁，一轮船自西向东航行，它在A处时测得小岛P位于北偏东60°，且A、P之间的距离为32海里，若轮船继续向正东方向航行，轮船有无触礁危险？请通过计算加以说明．如果有危险，轮船自A处开始至少沿东偏南多少度方向航行，才能安全通过这一海域？参考答案1．解：在格点三角形ADC中，AD＝2，CD＝4，∴AC＝＝＝2，∴cos C＝＝＝．故选：B．2．解：∵cos A＝sin（90°﹣A），余弦函数随角增大而减小，∴当0°＜∠A＜45°时，sin A＜cos A，即sin A﹣cos A＜0．故选：B．3．解：∵sinα+cosα＝，∴（sinα+cosα）2＝2，即sin2α+cos2α+2sinαcosα＝2．又∵sin2α+cos2α＝1，∴2sinαcosα＝1．∴（sinα﹣cosα）2＝sin2α+cos2α﹣2sinαcosα＝1﹣2sinαcosα＝1﹣1＝0．∴sinα﹣cosα＝0．故选：D．4．解：①∵sinα随α的增大而增大，∴若α＜β，则sinα＜sinβ，此结论正确；②∵cosα随α的增大而减小，∴若α＜β，则cosα＞cosβ，此结论错误；③∵tanα随α的增大而增大，∴若α＜β，则tanα＜tanβ，此结论正确；④若α+β＝90°，则sinα＝cosβ，此结论正确；综上，正确的结论为①③④，故选：C．5．解：∵2＝135°，∴∠2的补角＝180°﹣135°＝45°，∴∠1＝90°﹣45°＝45°，则tan∠1＝tan45°＝1．故选：C．6．解：用科学计算器计算锐角α的三角函数值时，只能计算正弦、余弦、正切的值，要计算余切的值，需先计算正切值，在借助倒数进行计算得出答案，故选：A．7．解：∵等腰三角形的周长是底边长的5倍，设底边为a，则腰长为2a．作AD⊥BC于D点，CE⊥AB于E点．∴AB＝AC＝2a，BD＝a，在Rt△ABD中，AD＝＝，∵S△ABC＝BC•AD＝AB•CE，∴CE＝．∴sin∠BAC＝＝．故选：A．8．解：如图，过点A作AM⊥DC于点M，过点B作BN⊥DC于点N．则AB＝MN，AM＝BN．在直角△ACM，∵∠ACM＝45°，AM＝50m，∴CM＝AM＝50m．∵在直角△BCN中，∠BCN＝∠ACB+∠ACD＝60°，BN＝50m，∴CN＝（m），∴MN＝CM﹣CN＝50﹣（m）．则AB＝MN＝（50﹣）m．故选：C．9．解：在Rt△ABD中，∵sin∠ABD＝，∴AD＝4sin60°＝2（m），在Rt△ACD中，∵sin∠ACD＝，∴AC＝＝2（m）．故选：B．10．解：作DE⊥AB于点E．在直角△AED中，ED＝BC＝a，∠ADE＝α∵tan∠ADE＝，∴AE＝DE•tan∠ADE＝a•tanα．同理AB＝a•tanβ．∴DC＝BE＝AB﹣AE＝a•tanβ﹣a•tanα＝a（tanβ﹣tanα）．故选：D．11．解：如图，，由勾股定理，得OA＝＝2．sin∠1＝＝，故答案为：．12．解：cos36°＞cos37°．故答案为＞．13．解：如图，∵tan A＝＝，∴设AB＝5x，则BC＝4x，AC＝3x，则有：sin A+cos A＝+＝+＝，故答案为：．14．解：∵∠BAC＝90°，AD⊥BC，∴∠α+∠β＝90°，∠B+∠β＝90°，∠B+∠C＝90°，∴∠α＝∠B，∠β＝∠C，∴sinα＝sin B，故①正确；sinβ＝sin C，故②正确；∵在Rt△ABC中sin B＝，cos C＝，∴sin B＝cos C，故③正确；∵sinα＝sin B，cos∠β＝cos C，∴sinα＝cos∠β，故④正确；故答案为①②③④．15．解：在直角△ABC中，AC＝BC，则∠C＝90°，∵AB＝BC，∴∠CAB＝45°，∴sin∠CAB＝，∴BC＝×AB＝2．故答案为2．16．解：∵∠C＝90°，MN⊥AB，∴∠C＝∠ANM＝90°，又∵∠A＝∠A，∴△AMN∽△ABC，∴＝＝，设AC＝3x，AB＝4x，由勾股定理得：BC＝＝x，在Rt△ABC中，cos B＝＝＝．17．解：存在的一般关系有：（1）sin2A+cos2A＝1；（2）tan A＝．证明：（1）∵sin A＝，cos A＝，a2+b2＝c2，∴sin2A+cos2A＝＝1．（2）∵sin A＝，cos A＝，∴tan A＝＝，＝．18．解：（1）原式＝＝＝．（2）原式＝＝＝﹣＝﹣19．解：（1）Rt△ABC中，∠ACB＝90°，BC＝，cot∠ABC＝，∴AC＝，∵点D是AC的中点，∴CD＝AC＝，∴Rt△BCD中，BD＝＝；（2）如图，过C作CH⊥AB于H，∵BC＝，cot∠ABC＝，∴CH＝，BH＝1，∵CE＝CB，∴EH＝BH＝1，∵∠ACB＝90°，BC＝，AC＝，∴AB＝3，∴AE＝3﹣2＝1，∴△ACE的面积＝×AE×CH＝×1×＝．20．解：过点A作AE⊥CD于点E，∵∠BAC＝15°，∴∠DAC＝90°﹣15°＝75°，∵∠ADC＝60°，∴在Rt△AED中，∵cos60°＝＝＝，∴DE＝2，∵sin60°＝＝＝，∴AE＝2，∴∠EAD＝90°﹣∠ADE＝90°﹣60°＝30°，在Rt△AEC中，∵∠CAE＝∠CAD﹣∠DAE＝75°﹣30°＝45°，∴∠C＝90°﹣∠CAE＝90°﹣45°＝45°，∴AE＝CE＝2，∴sin45°＝＝＝，∴AC＝2，∴AB＝2+2+2≈2×2.4+2×1.7+2＝10.2≈10米．答：这棵大树AB原来的高度是10米．21．解：（1）延长BA交EF于一点G，如图所示，则∠DAC＝180°﹣∠BAC﹣∠GAE＝180°﹣38°﹣（90°﹣23°）＝75°；（2）过点A作CD的垂线，设垂足为H，在Rt△ADH中，∠ADC＝60°，∠AHD＝90°，∴∠DAH＝30°，∵AD＝3，∴DH＝，AH＝，在Rt△ACH中，∠CAH＝∠CAD﹣∠DAH＝75°﹣30°＝45°，∴∠C＝45°，∴CH＝AH＝，AC＝，则树高++（米）．22．解：（1）如图所示．（2）这棵大树不会被歪倒的烟囱砸着．∵在RT△AGC中，∠ACG＝45°．∴AG＝CG＝DB＝21（m）．在Rt△BCG中，BG＝CG×tan30°＝DB×tan30°＝21×＝7．（m）∴烟囱的高度AB＝21+7≈33.124（m）．∵33.124m＜35m．∴这棵大树不会被歪倒的烟囱砸着．23．解：过P作PB⊥AM于B，在Rt△APB中，∵∠P AB＝30°，∴PB＝AP＝×32＝16海里，∵16＜16，故轮船有触礁危险．为了安全，应改变航行方向，并且保证点P到航线的距离不小于暗礁的半径16海里，即这个距离至少为16海里，设安全航向为AC，作PD⊥AC于点D，由题意得，AP＝32海里，PD＝16海里，∵sin∠P AC＝＝＝，∴在Rt△P AD中，∠P AC＝45°，∴∠BAC＝∠P AC﹣∠P AB＝45°﹣30°＝15°．答：若轮船继续向正东方向航行，轮船有触礁危险．轮船自A处开始至少沿东偏南15°度方向航行，才能安全通过这一海域．。

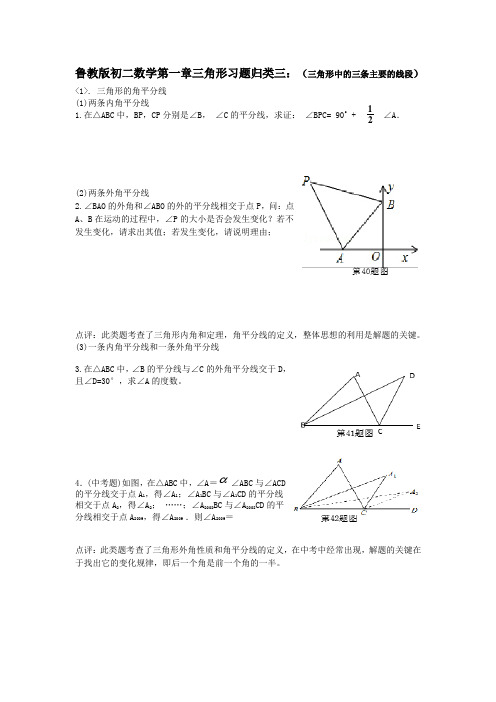
1鲁教版初二数学第一章三角形习题归类三：（三角形中的三条主要的线段）<1>. 三角形的角平分线(1)两条内角平分线 1.在△ABC 中，BP ，CP 分别是∠B ， ∠C 的平分线，求证： ∠BPC= 90˚ + ∠A ．(2)两条外角平分线2.∠BAO 的外角和∠ABO 的外的平分线相交于点P ，问：点A 、B 在运动的过程中，∠P 的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由；点评：此类题考查了三角形内角和定理，角平分线的定义，整体思想的利用是解题的关键。

(3)一条内角平分线和一条外角平分线3.在△ABC 中，∠B 的平分线与∠C 的外角平分线交于D ，且∠D=30°，求∠A 的度数。

4．(中考题)如图，在△ABC 中，∠A ＝ ∠ABC 与∠ACD的平分线交于点A 1，得∠A 1；∠A 1BC 与∠A 1CD 的平分线相交于点A 2，得∠A 2； ……；∠A 2008BC 与∠A 2008CD 的平分线相交于点A 2009，得∠A 2009 ．则∠A 2009＝点评：此类题考查了三角形外角性质和角平分线的定义，在中考中经常出现，解题的关键在于找出它的变化规律，即后一个角是前一个角的一半。

5.(2016内江）（1）如图1，O 是∠ABC 和∠ACB 的平分线的交点,∠A=∠α则∠BOC=___ 如图2 ，∠CBO= ∠ABC ,∠BCO= ∠ACB, ∠A=∠α则∠BOC=___ （2）如图3， ∠CBO=∠DBC ,∠BCO= ∠ECB, ∠A=∠α则∠BOC=___ 如图3 ，∠CBO= ∠DBC ,∠BCO= ∠ECB, ∠A=∠α则∠BOC=___<2>. 三角形的高线6.△ABC 中，∠A=60°,高BD 、CE 交于F ，则∠BFC ＝___7.已知BD 、CE 是△ABC 的高，直线BD 、CE 相交所成的角中有一个角为500，则∠BAC 等于 度．<3>. 三角形的中线8.在△ABC 中，S △ABC =60, AC=10，D 是AB 的中点，过点D 作DE AC 于点E ，则DE 的长是 。

鲁教版数学-九年级上册-第二章-直角三角形的边角关系-巩固练习一、单选题1.2sin60°的值等于（）A. 1B.C.D.2.如图，C岛在A岛的北偏东45°方向，C岛在B岛的北偏西25°方向，则从C岛看A、B两岛的视角∠ACB的度数是（）A. 70°B. 20°C. 35°D. 110°3.如图，市政府准备修建一座高AB为6m的过街天桥，已知∠ACB为天桥的坡面AC与地面BC的夹角，且sin∠ACB=，则坡面AC的长度为（）A. 6mB. 8mC. 10mD. 12m4.已知α、β都是锐角，如果sinα=cosβ，那么α与β之间满足的关系是（）A. α=βB. α+β=90°C. α﹣β=90°D. β﹣α=90°5.如图，四边形BDCE内接于以BC为直径的⊙A，已知：BC=10，cos∠BCD=，∠BCE=30°，则线段DE的长是（）A. B. 7 C. 4+3 D. 3+46.如果∠a是等腰直角三角形的一个锐角，则tana的值是（）A. B. C. 1 D.7.如图，为测量河两岸相对两电线杆A、B间的距离，在距A点16m的C处（AC⊥AB），测得∠ACB=52°，则A、B之间的距离应为（）A. 16sin52°mB. 16cos52°mC. 16tan52°mD. m8.如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tan∠ABC 的值为（）A. B. C. D. 19.如图，马航370失联后，“海巡31”船匀速在印度洋搜救，当它行驶到A处时，发现它的北偏东30°方向有一灯塔B，海巡船继续向北航行4小时后到达C处，发现灯塔B在它的北偏东60°方向．若海巡船继续向北航行，那么要再过多少时间海巡船离灯塔B最近？（）A. 1小时B. 2小时C. 小时D. 2小时二、填空题10.已知Rt△ABC中，∠C=90°，AC=3，∠B=37°，则BC的长为________（注：tan∠B=0.75，sin∠B=0.6，cos∠B=0.8）11.在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)12.将半径为12cm，弧长为12π的扇形围成圆锥（接缝忽略不计），那么圆锥的母线与圆锥高的夹角为________．13.若某斜面的坡度为，则该坡面的坡角为________度．14.一般地，当α，β为任意角时，cos（α+β）与cos（α﹣β）的值可以用下面的公式求得cos （α+β）=cosα•cosβ﹣sinα•sinβ；cos（α﹣β）=cosα•cosβ+sinα•sinβ．例如：cos90°=cos（30°+60°）=cos30°•cos60°﹣sin30°•sin60°= × ﹣× =0，类似地，可以求得cos15°的值是________（结果保留根号）．15.如图，P是∠α的边OA上一点，且P点的坐标为（3，4），则sin（90°﹣α）=________．16.求值：sin60°﹣tan30°=17.因为sin 30°= 210°=- ,所以sin 210°=sin(180°+30°)=-sin 30°;因为sin 60°= ,sin240°=- ,所以sin 240°=sin(180°+60°)=-sin 60°;由此猜想、推理知:一般地,当α为锐角时,有sin(180°+α)=-sin α;由此可知sin 225°=________.三、解答题18.如图，射线OA放置在由小正方形组成的网络中，现请你分别在图①、图②中添画（工具只能用直尺）射线OB，使tan∠AOB的值分别为1、．19.如图，直立于地面上的电线杆AB，在阳光下落在水平地面和坡面上的影子分别是BC、CD，测得BC=6米，CD=4米，∠BCD=150°，在D处测得电线杆顶端A的仰角为30°，试求电线杆的高度（结果保留根号）四、综合题20.如图，在△ABC中，AD是BC边上的高，AB=5，AD=4，BC=3+4 。

鲁教版（五四制）初三数学上册 直角三角形边与角的关系精选习题（有解析)1．如图，菱形ABCD 中，点E 、F 在对角线BD 上，BE=DF=14BD ，若四边形AECF 为正方形，则tan ∠ABE=_________．2．运算2sin30°+2cos60°+3tan45°=_______．3．在Rt △ABC 中，∠C=90°，下列式子不一定成立的是（ ） A ．sinA=sinB B ．cosA=sinB C ．sinA=cosB D ．∠A+∠B=90°4．已知△ABC 中，∠C=90°，AB=13，AC=5，则tanA=______． 5．已知等腰△ABC 中，AB=AC=13，BC=10，求底角∠B 的三种三角函数值．6．假如∠α是等边三角形的一个内角，那么cos α的值等于（ ） A ．12BCD ．17. 如图，已知⊙O 的半径为1，AB 与⊙O 相切于点A ，OB 与⊙O 交于点C ，CD ⊥OA ，垂足为D ，则c os ∠AOB 的值等于（ ）A.ODB.OAC.CDD.AB8．在△ABC 中，若│sinA-1│+）=0，则∠C=_______度． 9．△ABC 中，若，，则∠C=_______． 10．运算下列各题．（1）sin230°+cos245°sin60°·tan45°；（2）221cos 30cos 60tan 60tan 30-︒+︒︒⋅︒+tan60°11．在△ABC 中，若∠A ，∠B 满足│sinA +（cosB －12）2=0，则△ABC 是（ ）A ．等腰非等边三角形B ．等边三角形C ．直角三角形D ．钝角三角形12．求下列各式的值：OD CBA（1）2sin30°－3cos60°+tan45°； （2）cos270°+cos45°·si n45°+sin270°；（3）3tan30°－2tan45°+2cos30°； （4）2cos30°+5tan60°－2sin30°。

鲁教版七年级数学上1.1.3三角形的三边关系练习题【基础练习】1.(2019台州)下列长度的三条线段,能组成三角形的是( )(A)3,4,8 (B)5,6,10 (C)5,5,11 (D)5,6,112.(2020任城区期中)小红已有两根长度分别是10 cm、20 cm的木条,现要钉一个三角形木架,则她还需要第三根木条的长度可以是( )(A)5 cm (B)10 cm (C)20 cm (D)40 cm3.若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )(A)6 (B)7 (C)11 (D)124.(2020河口期中)一个等腰三角形的两边长分别是3 cm和7 cm,则它的周长是 cm.5.已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为6.已知一个三角形的三边长分别为2,8,x,若其周长是偶数,则x的值是;若x是奇数,则x的值是.7.一个三角形的两边长为3和5,(1)求它的第三边a的取值范围;(2)求它的周长L的取值范围;(3)若周长为偶数,求三角形的第三边长.8.已知等腰三角形的两边长a,b满足|a-4|+(b-9)2=0,求这个等腰三角形的周长.【综合训练】9.已知四根长度分别为3 cm,6 cm,8 cm,10 cm的木棒,任意选取三根木棒组成一个三角形,那么可以组成三角形的个数为( )(A)1个(B)2个 (C)3个(D)4个10.已知a,b,c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )(A)2a+2b-2c (B)2a+2b (C)2c (D)011.已知△A B C的周长为13,且各边长均为整数,那么这样的等腰△ABC有个.12.一个等腰三角形的周长为28 cm.(1)如果底边长是腰长的1.5倍,求这个等腰三角形的三边长;(2)如果一边长为10 cm,求这个等腰三角形的另两边长.【提高训练】13.(分论讨论题)某等腰三角形的三边长分别为x,3,2x-1,则该三角形的周长为( )(A)11 (B)11或8 (C)11或8或5 (D)与x的取值有关14.小明同学在研究了课本上的一道问题“四根小木棍的长度分别为2 cm,3 cm,4 cm和5 cm,任取其中3根,可以搭成几个不同的三角形?”后,提出下列问题:长度分别为a,b,c(单位: cm)的三根小木棍搭成三角形,已知a,b,c都是整数,且a≤b<c,如果b=5 cm,用满足上述条件的三根小木棍能够搭出几个不同的三角形?请你参与研究,并写出探究过程.。