鲁教版中考数学一轮复习 圆 专题2 与圆有关的位置关系(含答案)

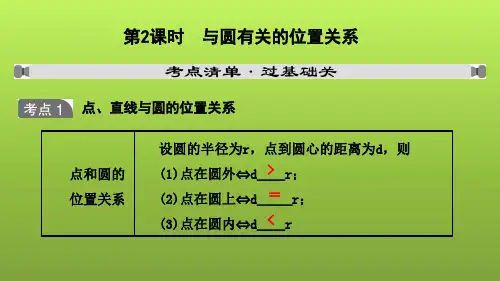
2024中考数学一轮复习核心知识点精讲—圆的基本性质与圆有关的位置关系1.探索并了解点和圆、直线和圆以及圆和圆的位置关系．2．知道三角形的内心和外心．3．了解切线的概念，并掌握切线的判定和性质，会过圆上一点画圆的切线.考点1：点与圆的位置关系设⊙O的半径是r，点P到圆心O的距离为d，则有：d<r⇔点P在⊙O内；d=r⇔点P在⊙O上；d>r⇔点P在⊙O外。

考点2：直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点；2、直线与圆相切⇒d r=⇒有一个交点；3、直线与圆相交⇒d r<⇒有两个交点；r d=r r dd考点3：切线的性质与判定定理1、切线的判定定理：过半径外端且垂直于半径的直线是切线；两个条件：过半径外端且垂直半径，二者缺一不可即：∵MN OA ⊥且MN 过半径OA 外端∴MN 是⊙O 的切线2、性质定理：切线垂直于过切点的半径（如上图）推论1：过圆心垂直于切线的直线必过切点。

推论2：过切点垂直于切线的直线必过圆心。

以上三个定理及推论也称二推一定理：即：①过圆心；②过切点；③垂直切线，三个条件中知道其中两个条件就能推出最后一个。

考点4：切线长定理切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，这点和圆心的连线平分两条切线的夹角。

即：∵PA 、PB 是的两条切线∴PA PB =；PO 平分BPA∠考点5：三角形的内切圆和内心（1）三角形的内切圆与三角形的各边都相切的圆叫做三角形的内切圆。

（2）三角形的内心三角形的内切圆的圆心是三角形的三条内角平分线的交点，它叫做三角形的内心。

注意：内切圆及有关计算。

（1）三角形内切圆的圆心是三个内角平分线的交点，它到三边的距离相等。

（2）△ABC 中，∠C=90°，AC=b ，BC=a ，AB=c ，则内切圆的半径r=2cb a -+。

（3）S △ABC =)(21c b a r ++，其中a ，b ，c 是边长，r 是内切圆的半径。

2019备战中考数学（鲁教版五四制）巩固复习-圆（含解析）一、单选题1.已知圆O的半径为3，圆心O到直线l的距离为5，则直线l和圆O的位置关系是（）A. 相离B. 相切C. 相交D. 以上均有可能2.已知：A，B，C，D，E五个点中无任何三点共线，无任何四点共圆，那么过其中的三点作圆，最多能作出（）A. 5个圆B. 8个圆C. 10个圆D. 12个圆3.下列命题中，假命题是（）A. 如果一条直线平分弦和弦所对的一条弧，那么这条直线经过圆心，并且垂直于这条弦； B. 如果一条直线平分弦所对的两条弧，那么这条直线经过圆心，并且垂直于这条弦；C. 如果一条直线经过圆心，并且平分弦，那么该直线平分这条弦所对的弧，并且垂直于这条弦；D. 如果一条直线经过圆心，并且垂直弦，那么该直线平分这条弦和弦所对的弧．4.已知OA=5cm，以O为圆心，r为半径作⊙O．若点A在⊙O内，则r的值可以是（）A. 3cmB. 4cmC. 5cmD. 6cm5.已知⊙O的半径为15，弦AB的长为18，点P在弦AB上且OP=13，则AP的长为（）A. 4B. 14C. 4或14D. 6或146.如图，AB为⊙O的直径，点C在⊙O上，∠A=40°，则∠B的度数为（）A. 20°B. 40°C. 50°D. 60°7.如图，已知，AB是⊙的直径，点C，D在⊙上，∠ABC=50°，则∠D为（）A. 50°B. 45°C. 40°D. 30°8.如图，AB为⊙O的直径，点C在⊙O上，若∠ACO=50°，则∠B的度数为（）A. 60°B. 50°C. 40°D. 30°9.如图O是圆心，半径OC垂直弦AB于点D，AB=8，OB=5，则OD等于（）A. 2B. 3C. 4D. 510.下列判断结论正确的有（）（1）直径是圆中最大的弦．（2）长度相等的两条弧一定是等弧．（3）面积相等的两个圆是等圆．（4）同一条弦所对的两条弧一定是等弧．（5）圆上任意两点间的部分是圆的弦．A.1个B.2个C.3个D.4个二、填空题11.如图，8×8的正方形网格纸上有扇形OAB和扇形OCD，点O，A，B，C，D均在格点上．若用扇形OAB围成一个圆锥的侧面，记这个圆锥的底面半径为r1；若用扇形OCD围成另个圆锥的侧面，记这个圆锥的底面半径为r2，则的值为________．12.如图，点A、D、G、M在半圆上，四边形ABOC、DEOF、HMNO均为矩形，设BC=a，EF=b，HN=c，则a、b、c三者间的大小关系为 ________13.如图，在Rt△ABC中，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E，∠BCD=40°，则∠A= ________14.如图，正六边形ABCDEF内接于⊙O，⊙O的半径为1，则弧AB的长为 ________.15.已知直线与⊙O相切，若圆心O到直线的距离是5，则⊙O的半径是________．16.如图是由两个长方形组成的工件平面图（单位：mm），直线l是它的对称轴，能完全覆盖这个平面图形的圆面的最小半径是________ mm．17.一个正八边形要绕它的中心至少转________ 度，才能和原来的图形重合，它有________ 条对称轴．18.在综合实践活动课上，小明用纸板制作了一个圆锥形漏斗模型．如图所示，它的底面半径OA=6cm，高SO=8cm，则这个圆锥漏斗的侧面积是________ cm2.(结果保留π)19.将一个圆心角为120°，半径为6cm的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为________．20.如果圆心O到直线l的距离等于⊙O的半径，那么直线l和⊙O的公共点有________个．三、解答题21.如图，已知AB是⊙O的弦，C是的中点，AB=8，AC= ，求⊙O半径的长．22.一堆圆锥形沙子，底面直径是8米，高是1.5米，如果每立方米沙子重1.5吨，那么这堆沙子重多少吨？23.如图所示，线段AD过圆心O交⊙O于D，C两点，∠EOD=78°，AE交⊙O于B，且AB=OC，求∠A的度数．四、综合题24.如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E．（1）求证：DE=DB；（2）若∠BAC=90°，BD=4，求△ABC外接圆的半径．25.如图，已知AB、AD是⊙O的弦，点C是DO的延长线与弦AB的交点，∠ABO=30°，OB=2．（1）求弦AB的长；（2）若∠D=20°，求∠BOD的度数．26.在平面直角坐标系xOy中，定义点P（x，y）的变换点为P′（x+y，x﹣y）．（1）如图1，如果⊙O的半径为，①请你判断M（2，0），N（﹣2，﹣1）两个点的变换点与⊙O的位置关系；②若点P在直线y=x+2上，点P的变换点P′在⊙O的内，求点P横坐标的取值范围．（2）如图2，如果⊙O的半径为1，且P的变换点P′在直线y=﹣2x+6上，求点P与⊙O 上任意一点距离的最小值．27.已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．（1）如图①，当直线l与⊙O相切于点C时，求证：AC平分∠DAB；（2）如图②，当直线l与⊙O相交于点E，F时，求证：∠DAE=∠BAF．答案解析部分一、单选题1.【答案】A【考点】直线与圆的位置关系【解析】【分析】圆O的半径为3，圆心O到直线l的距离为5；∵5>3，∴直线l和圆O的位置关系是相离。

中考复习之圆与圆的位置关系一、选择题：1.如果两圆的半径长分别为 6 和2，圆心距为 3，那么这两个圆的位置关系是【】A.外离B．相切C．相交D．内含2.若两圆的半径分别为 2cm 和6cm，圆心距为 4cm，则这两圆的位置关系是【】A.内含 B．内切 C．外切 D．外离3.如图，用邻边分别为 a，b（a＜b）的矩形硬纸板裁出以 a 为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆．把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽（拼接处材料忽略不计），则 a 与b 满足的关系式是【】A．b= a B．b= 5+1a2C．b=5a2D．b= 2a4.已知⊙O1与⊙O2外切，O1O2=8cm，⊙O1的半径为5cm，则⊙O2的半径是【】A.13cm.B. 8cmC. 6cmD. 3cm5.已知两圆半径分别为7，3，圆心距为4，则这两圆的位置关系为【】A.外离B.内切C.相交D.内含6.若⊙O1，⊙O2的半径是r1=2, r2=4，圆心距d=5，则这两个圆的位置关系是【】A.内切B.相交C.外切D.外离7.已知⊙O1、⊙O2的半径分别为3cm、5cm，且它们的圆心距为8cm，则⊙O1与⊙O2的位置关系是【】A.外切B．相交C．内切D．内含8.⊙O1和⊙O2的半径分别是3cm 和4cm，如果O1O2＝7cm，则这两圆的位置关系是【】A.内含B．相交C．外切D．外离9.若两圆的半径分别为2 和4，且圆心距为7，则两圆的位置关系为【】A.外切B. 内切C. 外离D. 相交10.如图，平面直角坐标系中，⊙O半径长为 1.点⊙P（a,0），⊙P的半径长为 2，把⊙P向左平移，当⊙P与⊙O相切时，a 的值为【】（A）3 （B）1 （C）1，3 （D）±1，±311.已知两圆外切，圆心距为5cm，若其中一个圆的半径是3cm，则另一个圆的半径是【】A.8cm B．5cm C．3cm D．2cm12.⊙O1的半径为3 厘米，⊙O2的半径为2 厘米，圆心距O1O2=5 厘米，这两圆的位置关系是【】A.内含B．内切C．相交D．外切13.已知两圆的半径分别为1 和3，当这两圆内含时，圆心距d 的范围是【】A. 0<d<2B. 1<d<2C. 0<d<3D. 0≤d<214.圆心距为2 的两圆相切，其中一个圆的半径为1，则另一个圆的半径为【】(A)1 (B)3 (C)1 或2 (D)1 或315.第三十奥运会将于 2012 年7 月27 日在英国伦敦开幕，奥运会旗图案有五个圆环组成，下图也是一幅五环图案，在这个五个圆中，不存在的位置关系是【】 A 外离 B 内切 C 外切 D 相交16.已知两圆相外切，连心线长度是 10 厘米，其中一圆的半径为 6 厘米，则另一圆的半径是【】A．16 厘米B．10 厘米C．6 厘米D．4 厘米17.如果两圆的半径分别为4 和6，圆心距为10，那么这两圆的位置关系是【】A.内含B．外离C．相交D．外切18.已知⊙O1与⊙O2的半径分别为4 和6，O1O2＝2，则⊙O1与⊙O2的位置关系是【】A.内切B．相交C．外切D．外离19.如图，⊙O1，⊙O，⊙O2的半径均为2cm，⊙O3，⊙O4的半径均为1cm，⊙O与其他4个圆均相外切，图形既关于O1O2所在直线对称，又关于O3O4所在直线对称，则四边形O1O4O2O3的面积为【】A．12cm2B．24cm2C．36cm2D．48cm220.已知两圆的半径分别是3 和4，圆心距的长为1，则两圆的位置关系为：【】A.外离B．相交C．内切D．外切21.已知两圆半径为5cm 和3cm，圆心距为3cm，则两圆的位置关系是【】A.相交B．内含C．内切D．外切22.定圆O 的半径是4cm，动圆P 的半径是2cm，动圆在直线l 上移动，当两圆相切时，OP 的值是【】A.2cm 或6cm B．2cm C．4cmD．6cm23.若两圆的半径是方程x2﹣5x+6=0 的两个根，且圆心距是5，则这两圆的位置关系是【】A.内切B．相交C．外切D．外离24.已知两圆的直径分别为2cm 和4cm，圆心距为3cm，则这两个圆的位置关系是【】A.相交B．外切C．外离D．内含25.已知两圆的半径分别为3cm、4cm，圆心距为8cm，则两圆的位置关系是【】A.外离B．相切C．相交D．内含二、填空题：1.半径分别为3cm 和4cm 的两圆内切，这两圆的圆心距为cm．2.如图，⊙M与⊙N外切，MN＝10cm，若⊙M的半径为6cm，⊙N的半径为cm。

2021中考数学一轮复习：与圆有关的位置关系一、选择题1. 如图，△ABC内心为I，连接AI并延长交△ABC的外接圆于D，则线段DI与DB的关系是()A.DI=DBB.DI>DBC.DI<DBD.不确定2. 下列说法中，正确的是()A．垂直于半径的直线是圆的切线B．经过半径的外端且垂直于这条半径的直线是圆的切线C．经过半径的端点且垂直于这条半径的直线是圆的切线D．到圆心的距离等于直径的直线是圆的切线3. 下列直线中，一定是圆的切线的是()A．与圆有公共点的直线B．垂直于圆的半径的直线C．到圆心的距离等于半径的直线D．经过圆的直径一端的直线4. △△△AB△△O△△△△B△△AOB△60°△△△A△△△△()A. 15°B. 30°C. 45°D. 60°5. 已知△O的半径为2，点P到圆心O的距离为4，则点P在()A．⊙O内B．⊙O上C．⊙O外D．无法确定6. 2019·泰安如图，△ABC是⊙O的内接三角形，∠A＝119°，过点C的圆的切线交BO 的延长线于点P ，则∠P 的度数为( )A ．32°B ．31°C ．29° D．61°7. 《九章算术》是我国古代内容极为丰富的数学名著，书中有下列问题：“今有勾八步，股十五步，问勾中容圆径几何．”其意思是：“今有直角三角形(如图)，勾(短直角边)长为8步，股(长直角边)长为15步，问该直角三角形能容纳的圆形(内切圆)的直径是多少．”答案是 ( )A ．3步B ．5步C ．6步D ．8步8. (2019•仙桃)如图，AB 为的直径，BC 为的切线，弦AD ∥OC ，直线CD 交的BA 延长线于点E ，连接BD ．下列结论：①CD 是的切线；②；③；④．其中正确结论的个数有A ．4个B ．3个C ．2个D ．1个二、填空题9. 直角三角形的两条直角边分别是5和12，则它的内切圆半径为 .10. 如图，△O 分别切△BAC 的两边AB ，AC 于点E ，F ，点P 在优弧上.若△BAC=66°，则△EPF 等于 度.O O O CO DB ⊥EDA EBD △∽△ED BC BO BE ⋅=⋅11. 如图1，已知△ABC的外心为O，BC＝10，∠BAC＝60°，分别以AB，AC 为腰向三角形外作等腰直角三角形ABD与ACE，连接BE，CD交于点P，则OP长的最小值是________．12. 如图，已知△ABC的内切圆⊙O与BC边相切于点D，连接OB，OD.若∠ABC ＝40°，则∠BOD的度数是________．13. 已知点P到⊙O上的点的最短距离为3 cm，最长距离为5 cm，则⊙O的半径为__________．14. 如图，已知AB＝AC＝AD，∠CBD＝2∠BDC，∠BAC＝44°，则∠CAD的度数为________．三、解答题15. 如图，城市A的正北方向50千米的B处，有一无线电信号发射塔．已知该发射塔发射的无线电信号的有效半径为100千米，AC是一条直达C城的公路，从A城发往C城的班车速度为60千米/时．(1)当班车从A城出发开往C城时，某人立即打开无线电收音机，班车行驶了0.5小时的时候，接收信号最强．此时，班车到发射塔的距离是多少千米？(离发射塔越近，信号越强)(2)班车从A城到C城共行驶2小时，请你判断到C城后还能不能接收到信号，并说明理由．图16. 如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且∠D ＝2∠A.(1)求∠D的度数；(2)若CD＝2，求BD的长．17. 如图，在△ABC中，AB＝6，AC＝BC＝5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E.(1)求证：DF⊥AC；(2)求CG的长.18. 如图，在平面直角坐标系中，O为坐标原点，点A的坐标为(0,4)，点B的坐标为(4,0)，点C的坐标为(－4,0)，点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P、D、B三点作⊙Q，与y轴的另一个交点为E，延长DQ 交⊙Q于F，连结EF、BF．（1）求直线AB的函数解析式；（2）当点P在线段AB（不包括A、B两点）上时．①求证：∠BDE＝∠ADP；②设DE＝x，DF＝y，请求出y关于x的函数解析式；（3）请你探究：点P在运动过程中，是否存在以B、D、F为顶点的直角三角形，满足两条直角边之比为2∶1？如果存在，求出此时点P的坐标；如果不存在，请说明理由．2021中考数学一轮复习：与圆有关的位置关系-答案一、选择题1. 【答案】A[解析]连接BI，如图，∵△ABC内心为I，∴∠1=∠2，∠5=∠6.∵∠3=∠1，∴∠3=∠2.∵∠4=∠2+∠6=∠3+∠5，∴∠4=∠DBI，∴DI=DB.故选A.2. 【答案】B3. 【答案】C4.【答案】B△△△△△AB △△O △△△△B △△OB △AB △△△ABO △90°△△△AOB △60°△△△A △90°△△AOB △90°△60°△30°.5. 【答案】C6. 【答案】A7. 【答案】C8. 【答案】A【解析】如图，连接．∵为的直径，为的切线，∴， ∵，∴，． 又∵，∴，∴．在和中，，∴，∴．又∵点在上，∴是的切线，故①正确， ∵，∴，∵，∴垂直平分，即，故②正确； ∵为的直径，为的切线，∴， ∴，∴，DO AB O BC O 90CBO ∠=︒AD OC ∥DAO COB ∠=∠ADO COD ∠=∠OA OD =DAO ADO ∠=∠COD COB ∠=∠COD △COB △CO CO COD COB OD OB =⎧⎪∠=∠⎨⎪=⎩COD COB △≌△90CDO CBO ∠=∠=︒D O CD O COD COB △≌△CD CB =OD OB =CO DB CO DB ⊥AB O DC O 90EDO ADB ∠=∠=︒90EDA ADO BDO ADO ∠+∠=∠+∠=︒ADE BDO ∠=∠∵，∴，∴， ∵，∴，故③正确；∵，，∴，∴，∵， ∴，故④正确，故选A ．二、填空题9. 【答案】2[解析]直角三角形的斜边==13，所以它的内切圆半径==2.10. 【答案】57[解析]连接OE ，OF .∵☉O 分别切∠BAC 的两边AB ，AC 于点E ，F ，∴OF ⊥AC ，OE ⊥AB ，∴∠BAC +∠EOF=180°，∵∠BAC=66°， ∴∠EOF=114°.∵点P 在优弧上，∴∠EPF=∠EOF=57°.故填:57.11. 【答案】5－533 [解析] ∵∠BAD ＝∠CAE ＝90°，∴∠DAC ＝∠BAE .在△DAC 和△BAE 中，⎩⎨⎧AD ＝AB ，∠DAC ＝∠BAE ，AC ＝AE ，∴△DAC ≌△BAE (SAS)， ∴∠ADC ＝∠ABE ，OD OB =ODB OBD ∠=∠EDA DBE ∠=∠E E ∠=∠EDA EBD △∽△90EDO EBC ∠=∠=︒E E ∠=∠EOD ECB △∽△ED ODBE BC=OD OB =ED BC BO BE ⋅=⋅从而∠PDB＋∠PBD＝90°，即∠DPB＝90°，从而∠BPC＝90°，∴点P在以BC为直径的圆上．如图，过点O作OH⊥BC于点H，连接OB，OC.∵△ABC的外心为O，∠BAC＝60°，∴∠BOC＝120°.又∵BC＝10，∴OH＝533，∴OP长的最小值是5－53 3.12. 【答案】70°[解析] 由切线长定理可知∠OBD＝12∠ABC＝20°.∵BC是⊙O的切线，∴OD⊥BC，∴∠BOD＝90°－∠OBD＝70°.13. 【答案】1 cm或4 cm[解析] 若点P在⊙O内，如图①.∵AP＝3 cm，BP＝5 cm，∴AB＝8 cm，∴OA＝4 cm；若点P在⊙O外，如图②.∵AP＝3 cm，BP＝5 cm，∴AB＝2 cm，∴OA＝1 cm.14. 【答案】[解析] ∵AB＝AC＝AD，∴点A是△BCD的外心，∴∠BAC＝2∠BDC.∵∠CBD＝2∠BDC，∴∠CBD＝∠BAC＝44°，∴∠CAD＝2∠CBD＝88°.三、解答题15. 【答案】解：(1)如图，过点B作BM⊥AC于点M，则班车行驶了0.5小时的时候到达点M.∵AM＝60×0.5＝30(千米)，AB＝50千米，∴BM＝40千米．答：此时，班车到发射塔的距离是40千米．(2)能．理由如下：如图，连接BC.∵AC＝60×2＝120(千米)，AM＝30千米，∴CM＝AC－AM＝120－30＝90(千米)，∴BC＝CM2＋BM2＝902＋402＝10 97(千米)＜100千米，∴到C城后还能接收到信号．16. 【答案】解：(1)连接OC.∵OA＝OC，∴∠A＝∠OCA，∴∠COD＝∠A＋∠OCA＝2∠A.∵∠D＝2∠A，∴∠COD＝∠D.∵PD与⊙O相切于点C，∴OC⊥PD，即∠OCD＝90°，∴∠D＝12×(180°－90°)＝45°.(2)由(1)可知∠COD＝∠D，∴OC＝CD＝2.由勾股定理，得OD＝22＋22＝2 2，∴BD＝OD－OB＝2 2－2.17. 【答案】解：(1)证明：如图，连接OD.∵DF 是⊙O 的切线，∴OD ⊥DF. ∵AC ＝BC ， ∴∠DBC ＝∠A.∵OD ＝OB ，∴∠DBC ＝∠ODB ， ∴∠A ＝∠ODB ，∴OD ∥AC ，∴DF ⊥AC. (2)如图，连接CD ，BG. ∵BC 是⊙O 的直径， ∴∠BGC ＝∠BDC ＝90°.∵AC ＝BC ，AB ＝6，∴AD ＝BD ＝12AB ＝3. 在Rt△ACD 中，CD ＝AC2－AD2＝52－32＝4. ∵AB·CD ＝2S△ABC ＝AC·BG ， ∴BG ＝AB·CD AC ＝6×45＝245， ∴CG ＝BC2－BG2＝52－（245）2＝75.18. 【答案】（1）直线AB 的函数解析式为y ＝－x ＋4． （2）①如图2，∠BDE ＝∠CDE ＝∠ADP ；②如图3，∠ADP ＝∠DEP ＋∠DPE ，如图4，∠BDE ＝∠DBP ＋∠A ， 因为∠DEP ＝∠DBP ，所以∠DPE ＝∠A ＝45°．所以∠DFE ＝∠DPE ＝45°．因此△DEF 是等腰直角三角形．于是得到y ．图2 图3 图4 （3）①如图5，当BD ∶BF ＝2∶1时，P (2,2)．思路如下：由△DMB ∽△BNF ，知122BN DM ==．设OD ＝2m ，FN ＝m ，由DE ＝EF ，可得2m ＋2＝4－m ．解得23m =． 因此4(0,)3D ．再由直线CD 与直线AB 求得交点P (2,2)． ②如图6，当BD ∶BF ＝1∶2时，P (8,－4)．思路同上．图5图6。

∴DE是⊙O的切线．
෾
(2)若∠C＝30°，CD＝2 ，求的长．
(2)解：如图，连接AD．∵AB是直径，∴∠ADB＝90°.∵AB＝AC，
∠C＝30°，∴∠B＝∠C＝30°，BD＝CD．∴∠OAD＝60°.
∵OA＝OD，∴△AOD是等边三角形．
∴∠AOD＝60°.∴∠BOD＝180°—∠AOD＝120°.
cm，则点P的位置是（ C ）
A．在⊙O内
B．在⊙O上
C．在⊙O外
D．不能确定
2．(2023湖州二模)已知平面内有⊙O与直线AB，⊙O的半径为3 cm，
点O到直线AB的距离为3 cm，则直线AB与⊙O的位置关系是（ A ）
A．相切
B．相交
C．相离
D．不能判断
3．(2021青海)点P是非圆上一点，若点P到⊙O上的点的最小距离是4
第25节
与圆有关的位置关系
知识梳理
1.点与圆的位置关系：
若⊙O的半径为r，平面内一点到圆心O的距离为d，则：
点在圆外
d＝OA>r
点在圆上
d＝OB＝r
点在圆内
d＝OC<r
1.已知⊙O的半径r＝10 cm，点P到圆心O的距离为d.
(1)当d＝8 cm时，点P在⊙O 内 ；
(2)当d＝10 cm时，点P在⊙O 上 ；
个内角平分线的交点．
5.已知△ABC的内切圆⊙O与各边相切于点D，E，F，那么点O是
△DEF的（ D ）
A．三条中线的交点
B．三条高的交点
C．三条角平分线的交点
D．三条边的垂直平分线的交点
核心考点
点与圆、直线与圆的位置关系
1．(2023柳州模拟)若⊙O的半径为6 cm，点P到圆心O的距离PO＝8

解：如图所示．
【问题情境2——示例】 2．(2021·济宁节选)如图，点C在以AB为直径的⊙O上，点D是BC的中点， 连接OD并延长交⊙O于点E，作∠EBP＝∠EBC，BP交OE的延长线于点P. 求证：PB是⊙O的切线．
证明：如图，连接OC，易得∠COE＝2∠CBE. ∵∠CBE＝∠EBP，∴∠CBP＝2∠CBE.∵点D是BC的中点， ∴OP⊥BC，∠BOE＝∠COE，∴∠BOE＝∠CBP， ∠OBD＋∠BOD＝90°，∴∠CBP＋∠OBD＝90°， 即∠OBP＝90°. 又∵点B在圆上，OB为⊙OC．相切
D．相交或相切
2.(2021·青海)P是非圆上一点，若点P到⊙O上的点的最小距离是4 cm，
最大距离是9 cm，则⊙O的半径是 6.5 cm或2.5 cm .
三角形的内切圆
三角形 的内切
圆
与三角形三边都__相__切___的圆叫做三角形的内切圆，内切圆 的圆心叫做三角形的__内__心___
1.(2021·泰安)如图，在△ABC中，AB＝6，以点A为圆心，3为半径的圆与边 BC相切于点D，与AC，AB分别交于点E和点G，F是优弧GE上一点，∠CDE＝ 18°，则∠GFE的度数是( B ) A．50° B．48° C．45° D．36°
2．(2021·临沂)如图，PA，PB分别与⊙O相切于点A，B，∠P＝70°， C为⊙O上一点，则∠ACB的度数是( C ) A．110° B．120° C．125° D．130°
第2课时 与圆有关的位置关系
点、直线与圆的位置关系
点和圆的 位置关系
设圆的半径为r，点到圆心的距离为d，则 (1)点在圆外⇔d__>__r； (2)点在圆上⇔d__＝___r； (3)点在圆内⇔d__<__r

九年级数学中考第一轮（七）圆鲁教版知识精讲【本讲教育信息】一. 教学内容：中考第一轮（七）圆二. 知识学习：1. 圆的基础知识①圆的有关概念：弦，弧，半圆，弓形，弓形高，等弧（隐含同圆等圆），弦心距，直径等。

②圆的确定圆心决定位置，半径决定大小，不共线的三点确定一个圆。

注意：作图（两边中垂线找交点），三角形外心的位置，外心到三角形各顶点距离等③圆的对称性：轴对称，中心对称，旋转不变性2. 圆与其它图形<1>点与圆三种<2>直线与圆①一条直线与圆三种②两条直线与圆③三条直线与圆三角形内切圆与圆外切三角形三角形内心（角平分线交点）位置永远在三角形内部，到三角形各边距离相等④四条直线与圆圆外切四边形两组对边的和相等+=+AB DC AD BC<3>两圆与直线两圆外切时连心线过内公切线，切点与该切线垂直。

两圆内切时连心线过切点，垂直于过切点的切线。

两圆相交时，连心线垂直于公共弦，并且平分公共弦。

3. 定理<1>垂径定理及推论：过圆心；垂直弦；平分弦（非直径）；平分优弧；平分劣弧；2求3。

<2>圆心角，弦，弦心距，弧之间关系：同圆等圆中知1得3。

<3>与圆有关的角：圆心角，圆周角，弦切角，圆内角，圆外角，圆内接四边形外角，内对角，对角<4>切线的判定、性质：①判定：常见的证法连半径，证垂直，判断切线，“连垂切”或作垂直证d＝r②性质：若一条直线满足过圆心、过切点，垂直于切线中任意两条，可得另外一条。

常见“切连垂”<5>切线长定理 从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角 4. 和圆有关的计算 < 1 >求线段 ①直径、半径②垂径定理：求弦长、弦心距、拱高③切线长④直角三角形内切圆半径⑤任意三角形内切圆半径与面积、周长的关系 ⑥等边三角形内切圆半径：外接圆半径=1：2 ⑦与圆有关的比例线段、弦长、切线长等 < 2 >求角圆心角，圆周角，弦切角，两切线夹角，公切线夹角 < 3 >正多边形的有关计算正n 边形的半径和边心距把正n 边形分成2n 个全等的直角三角形。

第2节 与圆有关的位置关系(必考,6~9分)命题分析【知识清单】知识点1 与圆有关的位置关系图1点与圆的位置关系 (设圆的半径为r , 平面内任一点到圆心的距离为d ){点在圆外⇔d① r,如图1中点A 点在圆上⇔d② r,如图1中点B 点在圆内⇔d③ r,如图1中点C直线与圆的位置关系(设圆的半径为r ,圆心到直线的距离为d )知识点2 切线切线的性质:圆的切线⑦ 于过切点的半径(或直径)切线的判定{若直线与圆的公共点已知,则连接过这点的半径,证明这条半径与要证直线垂直即可可简述为有公共点,连半径,证垂直若直线与圆的公共点未知,则过圆心作要证直线的垂线,证明垂线段的长等于圆的半径即可可简述为无公共点,作垂直,证半径图2切线长定理:从圆外一点可以引圆的两条切线,它们的切线长⑧ ,这一点和圆心的连线⑨ 两条切线的夹角,如图2,过☉O 外一点P 可引两条切线PA ,PB ,则PA=⑩ ,PO 平分∠APB知识点3 三角形的内心{定义:⑪ 叫做三角形的内切圆,⑫ 叫做三角形的内心性质:三角形的内心到三角形⑬ 的距离相等.三角形的内心是⑭ 的交点【参考答案】①> ②= ③< ④> ⑤= ⑥< ⑦垂直 ⑧相等 ⑨平分 ⑩PB与三角形各边相切的圆三角形内切圆的圆心各边三条角平分线【自我诊断】1.已知☉O 的半径为3,OA=5,则点A 在 ( )A .在☉O 外B .在☉O 上C .在☉O 内 D.无法确定2.在平面直角坐标系中,以点(-3,4)为圆心,3为半径的圆 ( ) A .与x 轴相离,与y 轴相切 B .与x 轴相离,与y 轴相交 C .与x 轴相切,与y 轴相交 D.与x 轴相切,与y 轴相离3.如图,P为☉O外一点,PA为☉O的切线,A为切点,PO交☉O于点B,∠P=30°,OB=3,则线段OP的长为( )A.3B.3√3C.6D.94.如图,☉O与△ABC的边AB,AC,BC分别相切于点D,E,F,如果AB=4,AC=5,AD=1,那么BC 的长为.【参考答案】1.A2.A3.C4.7【真题精粹】考向切线的性质与判定(必考)1.(2023·江西)如图,在△ABC中,AB=4,∠C=64°,以AB为直径的☉O与AC相交于点D,E为⏜上一点,且∠ADE=40°.ABD⏜的长.(1)求BE(2)若∠EAD=76°,求证:CB为☉O的切线.2.(2019·江西)如图1,AB 为半圆的直径,点O 为圆心,AF 为半圆的切线,过半圆上的点C 作CD ∥AB 交AF 于点D ,连接BC.(1)连接DO ,若BC ∥OD ,求证:CD 是半圆的切线.(2)如图2,当线段CD 与半圆交于点E 时,连接AE ,AC ,判断∠AED 和∠ACD 的数量关系,并证明你的结论.图1 图23.(2018·江西)如图,在△ABC 中,O 为AC 上一点,以点O 为圆心,OC 为半径作圆,与BC 相切于点C ,过点A 作AD ⊥BO 交BO 的延长线于点D ,且∠AOD=∠BAD. (1)求证:AB 为☉O 的切线.(2)若BC=6,tan ∠ABC=43,求AD 的长.热点预测【参考答案】(2)略1.(1)10π92.(1)略(2)∠AED+∠ACD=90°.证明略3.(1)略(2)2√54.(1)略(2)154【核心突破】考点1点与圆的位置关系例题1已知☉O的半径为8 cm.(1)在同一个平面内,若点P到圆心O的距离为5 cm,则点P在☉O .(填“内”、“上”或“外”)(2)如图,若P是☉O外一点,且PO=12 cm,Q是☉O上的一个动点,则PQ的最小值是,PQ的最大值是.解题指南变式特训1.P是非圆上一点,若点P到☉O上的点的最小距离是4 cm,最大距离是10 cm,则☉O的半径是.考点2线与圆的位置关系例题2如图,在Rt△ACB中,∠C=90°,BC=3,AC=4.(1)以C为圆心,3为半径的☉C与直线AB的位置关系是.(2)以点B为圆心,3为半径的☉B与直线AC的位置关系是.(3)以点A为圆心,3为半径的☉A与直线BC的位置关系是.例题3如图,在☉O中,点O为圆心,半径为5,AB为圆上的一条弦,且AB=8,C为☉O上一动点,过点C作CD⊥AB于点D.⏜上时,求CD的最大值及△ABC面积的最大值.(1)如图1,当点C在劣弧AB⏜上时,求CD的最大值及△ABC面积的最大值.(2)如图2,当点C在优弧AB考点3 切线的性质与判定例题4如图,AB 为☉O 的直径,C 为☉O 上一点,过点C 作☉O 的切线交AB 的延长线于点D ,DB=13AD ,连接AC ,若AB=4,则AC 的长为( )A .2√5B .72C .4 D.2√3变式特训2.如图,PA ,PB 分别与☉O 相切于A ,B 两点,C 为☉O 上一点,连接AC ,BC ,若∠P=80°,则∠ACB 的度数为 ( )A .80°B .40°C .50°D.70°3.如图,在△ABC 中,以AB 为直径作☉O 交AC ,BC 于点D ,E ,且D 是AC 的中点,过点D 作DG ⊥BC 于点G ,交BA 的延长线于点H. (1)求证:直线HG 是☉O 的切线. (2)若HA=3,cos B=25,求CG 的长.4.如图,在△ABC中,∠BAC=90°,过点A,B的☉O分别交AC,BC于点D,E,AB=AE,CD的垂直平分线交BC于点F,连接DF.(1)求证:DF是☉O的切线.(2)已知EF=3,DE=4,求BE和AB的长.方法提炼考点4切线长定理例题5如图,从☉O外一点P引☉O的两条切线PA,PB,切点分别为A,B,如果∠APB=60°,PA=8,那么弦AB 的长为( )A.8B.4C.4√3D.8√3变式特训5.如图,这是用一把直尺、含60°角的直角三角板和光盘摆放而成的图形,A为60°角与直尺的交点,B 为光盘与直尺唯一的交点,若AB=3,则光盘的直径是( ) A.6√3B.3√3C.6 D.3考点5三角形的内心和外心例题6如图,在正方形ABCD中,E是对角线BD上一点(不与点B重合),若点O是△BEC的内心,则∠COE( )A.大小为定值,等于112.5°B.大小不确定,可以等于90°C.大小为定值,等于127.5°D.大小不确定,随着点E的变化而变化变式特训6.如图,在正方形网格中,A,B,C,D,E,P均在格点处,则点P是下列哪个三角形的外心( )A.△ACEB.△ABDC.△ACDD.△BCE7.如图,在Rt△ABC中,内切圆O的半径为r,☉O与△ABC各边分别相切于点D,E和F,已知AD=3,BD=2,则r的值为.【参考答案】例题1(1) 内(2) 4 cm20 cm变式特训1.7 cm或3 cm例题2(1)相交(2)相切(3)相离例题3(1)CD=2,△ABC面积的最大值=8(2)CD=8,△ABC面积的最大值=32例题4 D变式特训2.C3.(1)略(2)654.(1)略(2)BE=163,AB=8√53例题5 A 变式特训5.A例题6 A 变式特训6.D7.111。

学校班级姓名【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】第27课时 与圆有关的位置关系班级： 姓名：学习目标: 1. 探索并了解点与圆的位置关系，了解直线与圆的位置关系及三角形内切圆的概念，会判断图形的位置关系．2. 掌握切线的概念，探索切线与过切点的半径的关系，会用三角尺过圆上一点画圆的切线．3. 探索并证明切线长定理，会利用它进行证明和相关计算重难点：灵活运用切线的性质定理和判定定理进行相关计算和证明． 学习过程 一．知识梳理1.点与圆的位置关系：如果设圆的半径为r ，点到圆心的距离为d ，那么： ①d r < ⇔点在 ． ②d r ＝ ⇔点在 ． ③d r > ⇔点在 ．2.直线与圆的位置关系：如果⊙O 的半径为r ，圆心O 到直线l 的距离为d ，那么： ①d r < ⇔ 直线l 与圆 ． ②d r ＝ ⇔ 直线l 与圆 ． ③d r > ⇔ 直线l 与圆 ．3.与圆有 公共点的直线叫做圆的切线，唯一的公共点叫做 ． 切线的判定定理：经过半径的外端并且 于这条半径的直线是圆的切线． 性质定理：圆的切线垂直于经过 的半径．4.在经过圆外一点的圆的切线上，这点和切点之间 的长，叫做这点到圆的切线长．切线长定理：从圆外一点引圆的两条切线，它们的切线长 ，圆心和这一点的连线 两条切线的夹角．5.与三角形各边 的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的 ，这个三角形叫做圆的 三角形． 、典型例题 1.点与圆的位置关系（2017宁夏）如图，点A B C ，，均在6×6的正方形网格格点上，过A B C ，，三点的外接圆除经过A B C ，，三点外还能经过的格点数为 ． 2.切线的性质与判定（1）（2017自贡）AB 是⊙O 的直径，PA 切⊙O 于点A ，PO 交⊙O 于点C ;连接BC,若P40∠=,则B∠等于（）A.20°B.25°C. 30°D.40°（2）（中考指要例1）（2017南充）如图，在Rt△ABC中，90ACB∠=︒，以AC为直径作⊙O交AB于点D，E为BC的中点，连接DE并延长交AC的延长线于点F．①求证：DE是⊙O的切线；②若24CF DF==，，求⊙O直径的长．（3）（中考指要例3）（2015青海）如图，在△ABC中，60B∠=︒，⊙O是△ABC的外接圆，过点A作⊙O的切线，交CO的延长线于点M，CM交⊙O于点D．①求证：AM AC=；②若3AC=，求MC的长．P COAB3.切线长定理与内切圆（1）(2016·荆州)如图，过⊙O 外一点P 引⊙O 的两条切线PA PB ，，切点分别是A B ，，OP 交⊙O 于点C ，D 是优弧上不与点A C ，重合的一个动点，连接AD CD ，.若80APB ∠︒＝，则 ADC ∠的度数是( )A.15°B. 20°C. 25°D. 30°（2）(2017·武汉)已知一个等腰三角形三角形的底边长为10，腰长为分别13，则其内切圆的半径为 三、中考预测（2017东营）如图，在△ABC 中，AB AC =，以AB 为直径的⊙O 交BC 于点D ，过点D 作⊙O 的切线DE ，交AC 于点E ，AC 的反向延长线交⊙O 于点F ． （1）求证：DE AC ⊥；（2）若8DE EA +=，⊙O 的半径为10，求AF 的长度．第6题图M GF EO CDBAN四、反思总结1.本节课你复习了哪些内容？2.通过本节课的学习，你还有哪些困难？五、达标检测1、（2015•湘西州）⊙O 的半径为5cm ，点A 到圆心O 的距离3OA cm =，则点A 与圆O 的位置关系为（ ） A ．点A 在圆上 B ． 点A 在圆内C ． 点A在圆外D ． 无法确定2、（2016嘉兴）如图，中，534AB BC AC ===，，，以点C 为圆心的圆与AB 相切，则⊙C的半径为（ ） A. 2.3B.2.4C.2.5D.2.63、（2016南京）如图，在矩形ABCD 中，45AB AD ==，，AD AB BC 、、分别与⊙O 相切于E F G 、、三点，过点D 作⊙O 的切线交BC 于点M ，切点为N ，则DM 的长为()A. 133B.92C.4133D. 254、（2016鄂州）如图，在△ABC 中，AB AC =，AE 是BAC ∠的平分线，ABC ∠的平分线 BM 交AE 于点M ，点O 在AB 上，以点O 为圆心，OB 的长为半径的圆经过点M ，交BC 于点G ，交 AB 于点F ．（1）求证：AE 为⊙O 的切线．（2）当812BC AC ==，时，求⊙O 的半径． （3）在（2）的条件下，求线段BG 的长．5、（中考指要例2）（2015温州）如图，AB 是半圆O 的直径，CD AB ⊥于点C ，交半圆于点E ，DF 切半圆于点F 。

简述质量管理体系的四级文件及作用Having a well-defined quality management system is essential for any organization to ensure that products and services consistently meet customer requirements. In order to establish and maintain such a system, four levels of documentation are typically required: quality manual, quality procedures, work instructions, and quality records. These documents play different but equally important roles in the effective implementation of a quality management system.建立一个明确定义的质量管理体系对于任何组织来说都是至关重要的，以确保产品和服务始终符合客户的要求。

为了建立和维护这样一个体系，通常需要四级文档：质量手册、质量程序、作业指导书和质量记录。

这些文档在有效实施质量管理体系中发挥着不同但同等重要的作用。

The quality manual serves as the top-level document that outlines the organization's quality policies, objectives, and overall approach to quality management. It provides a high-level overview of how the organization intends to meet customer expectations and regulatory requirements, setting the tone for the rest of the quality management system documentation. The quality manual is oftenused as a reference point for internal and external stakeholders to understand the organization's commitment to quality and continuous improvement.质量手册是最高级的文件，概述了组织的质量政策、目标和整体质量管理方法。

23.与圆有关的位置关系基础训练1.⊙O的半径为8，圆心O到直线l的距离为4，则直线l与⊙O的位置关系是（）A. 相切B. 相交C. 相离D. 不能确定2. (2020重庆A卷)如图，AB是⊙O的切线，A为切点，连接OA，OB，若∠B＝20°，则∠AOB的度数为（）A. 40°B. 50°C. 60°D. 70°3. (2020通辽)如图，P A，PB分别与⊙O相切于A，B两点，∠P＝72°，则∠C＝（）A. 108°B. 72°C. 54°D. 36°第3题图4.(2020南京)如图，在平面直角坐标系中，点P在第一象限，⊙P与x轴、y轴都相切，且经过矩形AOBC的顶点C，与BC相交于点D.若⊙P的半径为5，点A的坐标是(0，8)，则点D的坐标是（）A. (9，2)B. (9，3)C. (10，2)D. (10，3)第4题图5.(2020徐州)如图，AB是⊙O的弦，点C在过点B的切线上，OC⊥OA，OC交AB于点P.若∠BPC ＝70°，则∠ABC的度数等于（）A. 75°B. 70°C. 65°D. 60°6. (2020金华)如图，⊙O 是等边△ABC 的内切圆，分别切AB ，BC ，AC 于点E ，F ，D ，P 是DF ︵上一点，则∠EPF 的度数是（ ）A. 65°B. 60°C. 58°D. 50°第6题图7. (2020温州)如图，菱形OABC 的顶点A ，B ，C 在⊙O 上，过点B 作⊙O 的切线交OA 的延长线于点D ，若⊙O 的半径为1，则BD 的长为（ ）A. 1B. 2C. 2D. 3第7题图8. 如图，直线a ⊥b ，垂足为H ，点P 在直线b 上，PH ＝4 cm ，O 为直线b 上一动点，若以1 cm 为半径的⊙O 与直线a 相切，则OP 的长为 cm.第8题图9. (2020枣庄)如图，AB 是⊙O 的直径，P A 切⊙O 于点A ，线段PO 交⊙O 于点C.连接BC ，若∠P ＝36°，则∠B ＝ ．第9题图10. (2020泰州)如图所示的网络由边长为1个单位长度的小正方形组成，点A 、B 、C 在直角坐标系中的坐标分别为(3，6)、(－3，3)、(7，－2)，则△ABC 内心的坐标为 ．第10题图11. (2020杭州)如图，已知AB 是⊙O 的直径，BC 与⊙O 相切于点B ，连接AC ，O C.若sin ∠BAC ＝13，则tan ∠BOC ＝ ．第11题图12. (鲁教九下P 37习题2改编)如图，AB 是⊙O 的直径，C 是⊙O 上的一点，AD 垂直于过点C 的切线，垂足为D ，∠BAD ＝70°，则∠DAC ＝ .第12题图13. (2019常州)如图，半径为3的⊙O 与边长为8的等边三角形ABC 的两边AB 、BC 都相切，连接OC ，则tan ∠OCB ＝ ．第13题图14. (2020陕西)如图，△ABC是⊙O的内接三角形，∠BAC＝75°，∠ABC＝45°.连接AO并延长，交⊙O 于点D，连接B D.过点C作⊙O的切线，与BA的延长线相交于点E.(1)求证：AD∥EC；(2)若AB＝12，求线段EC的长．第14题图15.(2020菏泽)如图，在△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，过点D作⊙O 的切线交AC于点E.(1)求证：DE⊥AC；(2)若⊙O的半径为5，BC＝16，求DE的长．第15题图16. (2020北京)如图，AB 为⊙O 的直径，C 为BA 延长线上一点，CD 是⊙O 的切线，D 为切点，OF ⊥AD 于点E ，交CD 于点F .(1)求证：∠ADC ＝∠AOF ；(2)若sin C ＝13，BD ＝8，求EF 的长．第16题图17. (2020衡阳)如图，在△ABC 中，∠C ＝90°，AD 平分∠BAC 交BC 于点D ，过点A 和点D 的圆，圆心O 在线段AB 上，⊙O 交AB 于点E ，交AC 于点F .(1)判断BC 与⊙O 的位置关系，并说明理由； (2)若AD ＝8，AE ＝10，求BD 的长．第17题图巩固训练18. (2020湖州)如图，已知OT 是Rt △ABO 斜边AB 上的高线，AO ＝BO ，以O 为圆心，OT 为半径的圆交OA 于点C ，过点C 作⊙O 的切线CD ，交AB 于点D.则下列结论中错误．．的是（ ） A. DC ＝DT B. AD ＝2DT C. BD ＝BO D. 2OC ＝5AC第18题图19. (2020眉山)如图，点P 为⊙O 外一点，过点P 作⊙O 的切线P A 、PB , 点A 、B 为切点．连接AO 并延长交PB 的延长线于点C ，过点C 作CD ⊥PO ，交PO 的延长线于点D.已知P A ＝6，AC ＝8，则CD 的长为 ．第19题图20. 如图，已知BD 为⊙O 的直径，AB 为⊙O 的一条弦，P 是⊙O 外一点，且PO ⊥AB ，垂足为C ，PO 交⊙O 于点N 和点M ，连接BM ，AD ，AP .设BC ＝x ，(1)求证：PM ∥AD ；(2)若∠BAP ＝2∠M ，求证：P A 是⊙O 的切线；(3)连接BN ，若AD ＝6，tan M ＝12.用含x 的代数式表示MN ；第20题图21. (2020大庆)如图，在△ABC 中，AB ＝AC ，以AB 为直径的⊙O 交BC 于点D ，连接AD ，过点D 作DM ⊥AC ，垂足为M ，AB 、MD 的延长线交于点N .(1)求证：MN 是⊙O 的切线； (2)求证：DN 2＝BN ·(BN ＋AC )； (3)若BC ＝6，cos C ＝35，求DN 的长．第21题图参考答案1. B 【解析】∵⊙O 的半径为8，圆心O 到直线l 的距离为4，∵8>4，即d <r ，∴直线l 与⊙O 的位置关系是相交．2. D 【解析】∵AB 是⊙O 的切线，∴∠OAB ＝90°，∴∠AOB ＝90°－∠B ＝90°－20°＝70°.3. C 【解析】如解图，连接OA ，OB ，∵直线P A ，PB 分别与⊙O 相切于点A ，B ，∴OA ⊥P A ，OB ⊥P B.∵∠P ＝72°，∴∠AOB ＝108°.∵C 是⊙O 上一点，∴∠ACB ＝12∠AOB ＝54°.第3题解图4. A 【解析】如解图，设⊙P 与y 轴切于点N ，与x 轴切于点M ，连接PN 、PM ，延长NP 交CD 于点E ，得矩形ANEC ，∴CE ＝DE ，∵OA ＝8，PM ＝PN ＝5，∴DE ＝CE ＝AN ＝8－5＝3，∴DB ＝8－6＝2，连接PC ，在Rt △PCE 中，由勾股定理可得：PE ＝PC 2－CE 2＝52－32＝4，∴OB ＝OM ＋BM ＝OM ＋PE ＝5＋4＝9，∴D 点的坐标为(9，2)．第4题解图5. B 【解析】∵∠BPC ＝70°，∴∠APO ＝70°，∵OC ⊥OA ，∴∠AOP ＝90°，∴∠OAP ＝20°，∵OA ＝OB ，∴∠ABO ＝20°，又∵BC 是⊙O 的切线，∴∠OBC ＝90°，∴∠ABC ＝∠OBC －∠ABO ＝90°－20°＝70°.6. B 【解析】如解图，连接OE ，OF .∵AB ，BC 为⊙O 的切线，∴∠OEB ＝∠OFB ＝90°.∵△ABC 是等边三角形，∴∠B ＝60°，∴∠EOF ＝120°，∴∠EPF ＝12∠EOF ＝60°.第6题解图7. D 【解析】如解图，连接OB ，∵四边形OABC 是菱形，∴AB ＝OA ，又∵OA ＝OB ，∴△OAB 为等边三角形，∴∠AOB ＝60°，∵BD 是⊙O 的切线，∴∠DBO ＝90°，∵OB ＝1，∴BD ＝3OB ＝ 3.第7题解图8. 3或5 【解析】当圆在直线a 的左边时，PO ＝PH －OH ＝4－1＝3，当圆在直线a 的右边时，PO ＝PH ＋OH ＝4＋1＝5.9. 27° 【解析】∵P A 与⊙O 相切，∴∠P AO ＝90°，∴∠AOP ＝90°－∠P ＝54°，∴∠B ＝12∠AOP ＝27°.10. (2，3) 【解析】如解图，先根据三点坐标确定两坐标轴的位置，再找出内心．第10题解图11.22 【解析】∵sin ∠BAC ＝13，∴BC AC ＝13，设BC ＝x (x >0)，则AC ＝3x ，∴AB ＝（3x ）2－x 2＝22x .∵AB 为⊙O 的直径，∴OB ＝12AB ＝2x ，∴tan ∠BOC ＝BC OB ＝x 2x ＝22.12. 35° 【解析】如解图，连接O C.∵OA ＝OC ，∴∠ACO ＝∠CAO .∵CD 切⊙O 于点C ，∴OC ⊥CD ，又∵AD ⊥CD ，∴AD ∥CO ，∴∠DAC ＝∠ACO ，∴∠DAC ＝∠CAO ，即AC 平分∠BAD ，∴∠DAC ＝12∠BAD＝35°.第12题解图13.35【解析】如解图，过点O 作OD ⊥BC 于点D ，连接OB ，∵△ABC 是等边三角形，∴∠ABC ＝60°，∵AB 、BC 两边都与⊙O 相切，∴∠OBD ＝30°，在Rt △OBD 中，tan30°＝OD BD ＝3BD ＝33，∴BD ＝3，∵BC ＝8，∴CD ＝8－3＝5，∴tan ∠OCB ＝OD CD ＝35.第13题解图14. (1)证明：如解图，连接O C. ∵CE 与⊙O 相切于点C ， ∴∠OCE ＝90°. 又∵∠ABC ＝45°， ∴∠AOC ＝90°＝∠OCE . ∴AD ∥EC ；第14题解图(2)解：如解图，过点A 作AF ⊥EC 于点F . ∵OA ＝OC ，∴四边形AOCF 为正方形． ∵∠OAC ＝45°，∠BAC ＝75°，∴∠BAD ＝30°.在Rt △ABD 中，AD ＝ABcos 30°＝8 3.∴AF ＝CF ＝OA ＝12AD ＝4 3.∵AD ∥EC ， ∴∠E ＝∠BAD ＝30°.在Rt △AEF 中，EF ＝AFtan 30°＝12.∴EC ＝EF ＋FC ＝12＋4 3. 15. (1)证明：如解图，连接OD ，∵AB ＝AC ，∴∠B ＝∠C ，∵OB ＝OD ，∴∠B ＝∠ODB ，∴∠B ＝∠ODB ＝∠C ，∴OD ∥AC ，∵DE 是⊙O 的切线，∴OD ⊥DE ，∴DE ⊥AC ；第15题解图(2)解：如解图，连接AD ，∵AB 为直径，AB ＝AC ，∴AD 是等腰三角形ABC 的高，也是中线，∴CD ＝BD ＝12BC ＝12×16＝8，∠ADC ＝90°， ∵AB ＝AC ＝2×5＝10，在Rt △ACD 中，由勾股定理得：AD ＝102－82＝6，∵S △ACD ＝12DC ·AD ＝12AC ·DE ∴12×8×6＝12×10×DE ， ∴DE ＝4.8.16. (1)证明：如解图，连接OD ，第16题解图∵CD 是⊙O 的切线，∴CD ⊥OD ，∴∠ODA ＋∠ADC ＝90°.∵OF ⊥AD ，∴∠DOF ＋∠ODA ＝90°，∴∠ADC ＝∠DOF .∵OD ＝OA ，OF ⊥AD∴OF 平分∠AOD ，∴∠AOF ＝∠DOF ，∴∠ADC ＝∠AOF ；(2)解：设半径为r ，在Rt △OCD 中，sin C ＝13， ∴OD OC ＝13. ∴OD ＝r ，OC ＝3r .∵OA ＝r ，∴AC ＝OC －OA ＝2r .∵AB 为⊙O 的直径，∴∠ADB ＝90°.∴OF ∥B D.∴OE BD ＝AO AB ＝12. ∴OE ＝4.∵OF BD ＝OC BC ＝34， ∴OF ＝6.∴EF ＝OF －OE ＝2.17. 解：(1)BC 与⊙O 相切．理由：如解图，连接OD ，∵∠C ＝90°，∴∠ADC ＋∠DAC ＝90°.∵AD 平分∠BAC ，∴∠BAD ＝∠DA C.∵OA ＝OD ，∴∠BAD ＝∠ADO ＝∠DA C.∴∠ADC ＋∠ADO ＝90°.∴∠ODC ＝90°.∵OD 是⊙O 的半径，∴BC 与⊙O 相切；(2)如解图，连接DE ，第17题解图∵AE 为⊙O 的直径，∴在Rt △ADE 中，∠ADE ＝90°，∴DE ＝AE 2－AD 2＝102－82＝6.∴sin ∠EAD ＝DE AE ＝610＝35. 又∵∠EAD ＝∠DAC ，∴sin ∠DAC ＝35. 即CD AD ＝35，得CD ＝245， ∴在Rt △ACD 中，AC ＝AD 2－CD 2＝82－（245）2＝325. ∵OD ∥AC ，∴△BOD ∽△BAC ，得BD BC ＝OD AC ，即BD BD ＋245＝5325， 解得BD ＝1207. 18. D 【解析】如解图，连接OD ，∵∠AOB ＝90°，AO ＝BO ，∴△ABO 是等腰直角三角形．∵OT ⊥AB ，∴∠OTD ＝90°.∵CD 是⊙O 的切线，∴∠OCD ＝90°.∵OC ＝OT ，OD ＝OD ，∴Rt △OCD ≌Rt △OTD (HL)．∴DC ＝DT .故A 选项正确；∵△ABO 是等腰直角三角形，OT ⊥AB ，∴OT ＝AT ，∠A ＝45°.∵∠ACD ＝90°，∴△ACD 是等腰直角三角形．∴AD ＝2C D.∵DC ＝DT ，∴AD ＝2DT .故B选项正确；∵OC ＝OT ＝BT ，DC ＝DT ，∴AO ＝AC ＋OC ＝DC ＋OC ＝DT ＋BT ＝B D.∵AO ＝BO ，∴BD ＝BO .故C 选项正确；设AC ＝DT ＝x ，∵AD ＝2DT ，∴OC ＝OT ＝AT ＝(2＋1)x .∴2OC ＝(22＋2)x ，5AC ＝5x ，∴2OC ≠5AC ，故D 选项错误．第18题解图19. 25 【解析】如解图，连接OB ，∵P A ＝6，AC ＝8.∴在Rt △ACP 中，CP ＝P A 2＋AC 2＝62＋82＝10.在Rt △AOP 和Rt △BOP 中，⎩⎪⎨⎪⎧OP ＝OP OA ＝OB ，∴Rt △AOP ≌Rt △BOP (HL)，∴PB ＝P A ＝6.∴BC ＝PC －PB ＝10－6＝4.设OA ＝OB ＝r ，则OC ＝8－r ，在Rt △BOC 中，OB 2＋BC 2＝OC 2，即42＋r 2＝(8－r )2，解得r ＝3，∴OA ＝3，OC ＝5.在Rt △OP A 中，OP ＝OA 2＋P A 2＝32＋62＝3 5.∵∠COD ＝∠POA ，∠OAP ＝∠ODC ＝90°，∴△OAP ∽△ODC ，∴OC OP ＝CD P A ，即535＝CD 6，解得CD ＝2 5.第19题解图20. (1)证明：∵BD 是直径，∴∠DAB ＝90°.∵PO ⊥AB ，∴∠MCB ＝90°，∴∠DAB ＝∠MCB ，∴PM ∥AD ；(2)证明：如解图，连接O A.第20题解图∵∠BON ＝2∠M ，∠BAP ＝2∠M ，∴∠BON ＝∠BAP .∵OA ＝OB ，OC ⊥AB ，∴∠AOC ＝∠BON ，∴∠AOC ＝∠BAP .在Rt △OAC 中，∠AOC ＋∠OAC ＝90°，∴∠BAP ＋∠OAC ＝90°，即∠OAP ＝90°，∴P A ⊥OA ，∵OA 为⊙O 的半径，∴P A 是⊙O 的切线；(3)解：在Rt △MCB 中，tan M ＝12， ∴BC CM ＝12. ∵BC ＝x ，∴CM ＝2x .∵MN 是⊙O 直径，MN ⊥AB ，∴∠MBN ＝∠BCN ＝90°，∴∠NBC ＝90°－∠BNC ＝∠M ，∴tan ∠NBC ＝tan M ＝12， ∵tan ∠NBC ＝NC BC ＝12， ∴NC ＝12BC ＝12x ， ∴MN ＝2x ＋12x ＝52x . 21. (1)证明：如解图，连接OD ，第21题解图∵AB为⊙O的直径，∴∠ADB＝90°，∴AD⊥BC，∵AB＝AC，∴AD平分BC，即BD＝CD，∵OA＝OB，∴OD为△ABC的中位线，∴OD∥AC，∵DM⊥AC，∴OD⊥DM，∵OD是⊙O的半径，∴MN是⊙O的切线；(2)证明：∵MN是⊙O的切线，∴∠ODB＋∠BDN＝90°.∵OD＝OB，∴∠OBD＝∠ODB，∴∠OBD＋∠BDN＝90°.∵AB是⊙O的直径，∴∠DAB＋∠OBD＝90°，∴∠DAB＝∠BDN，∵∠BND＝∠DNA，∴△NDB∽△NAD，∴DNAN＝BNDN，即DN2＝BN·AN.∵AN ＝AB ＋BN ，AB ＝AC ，∴AN ＝BN ＋AC ，∴DN 2＝BN ·(BN ＋AC )；(3)解：∵AB ＝AC ，∠DAC ＝∠DAB ，∴∠C ＝∠ABD ＝∠ADM ，在Rt △ABD 中，cos ∠ABD ＝cos C ＝BD AB ＝35， ∵BC ＝6，∴BD ＝3，∴AB ＝5，在Rt △ABD 中，由勾股定理得AD ＝AB 2－BD 2＝52－32＝4，∴sin ∠ABD ＝AD AB ＝45， 在Rt △ADM 中，sin ∠ADM ＝sin ∠ABD ＝AM AD ＝45， ∴AM ＝165. ∵OD ∥AM ，∴△NDO ∽△NMA ，∴OD AM ＝NO NA ，即 52 165 ＝BN ＋52BN ＋5， 解得BN ＝457， 由(2)知DN 2＝BN ·(BN ＋AC )，即DN 2＝457×(457＋5)， ∴DN ＝607.。

与圆有关的位置关系基础知识知识点一、点与圆的位置关系1. 点和直线有三种位置关系：①点在圆外，即这个点到圆心的距离大于半径；②点在圆上，即这个点到圆心的距离等于半径；③点在圆内，即这个点到圆心的距离小于半径．2. 用数量关系表示位置关系：⊙O的半径为r，点P到圆心的距离OP＝d，则有①点P在⊙O外d＞r；②点P在⊙O上d＝r；③点P在⊙O内d＜r．知识点二、直线和圆的位置关系1．直线和圆的三种位置关系：（1）相离：直线和圆没有公共点，这时我们说这条直线和圆相离．（2）相切：直线和圆只有一个公共点，这时我们说这条直线和圆相切，这条直线叫做圆的切线，这个点叫做切点．（3）相交：直线和圆有两个公共点，这时我们说这条直线和圆相交．2、直线和圆的位置关系的性质与判断：设圆的半径为r，圆心到直线的距离为d，则：①直线和圆相离 d < r②直线和圆相切 d = r③直线和圆相交 d > r．知识点三、切线的判定定理1.切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．在应用定理时，必须先弄清两个条件：一是经过半径的外端；二是垂直于这条半径，两者缺一不可．2. 切线的判定方法有以下几种：①可以直接应用定义：直线与圆有一个公共点时，直线是圆的切线．②圆心到直线的距离等于半径的直线是圆的切线.③切线的判定定理．当已知条件中没有指出圆与直线的公共点时，常运用方法②进行判定；当已知条件中明确指出圆与直线有公共点时，常运用判定定理进行判定.证题方法“有点连半径，无点作垂线”.知识点四、切线的性质定理与切线长定理1. 切线的性质定理：圆的切线垂直于过切点的半径．当已知圆的切线时，常常连接过切点的半径，得两线垂直关系. 2.切线长定理（1）切线长的定义：过圆外一点作圆的切线，这点和切点之间的线段的长，叫做这点到圆的切线长． （2）切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等． 知识点五、三角形的外接圆与外心1. 三角形的外接圆：经过三角形的三个顶点的圆叫做三角形的外接圆．2. 三角形的外心：三角形外接圆的圆心，是三角形三条边垂直平分线的交点.这个点叫做三角形的外心．3. 三角形外心的性质：①三角形的外心是外接圆的圆心，它到三角形各顶点的距离相等；②三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的；但一个圆的内接三角形却有无数个，这些三角形的外心重合．知识点六、三角形的内切圆与内心1.三角形的内切圆是指与三角形各边都相切的圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．任意一个三角形都有且只有一个内切圆．但一个圆的外切三角形有无数个．2. 三角形的内心：三角形内切圆的圆心，是三角形三条角平分线的交点，到三角形三边的距离相等. 常见结论：（1）Rt △ABC 的三条边分别为：a 、b 、c （c 为斜边），则它的内切圆的半径2ab cr ； （2）△ABC 的周长为l ，面积为S ，其内切圆的半径为r ，则12S lr ． 知识点七、正多边形与圆的关系1. 正多边形的概念：各边相等，各角也相等的多边形叫做正多边形．2. 正多边形与圆的关系可以这样表述：把圆分成n （n≥3）等份，依次连接各分点所得的多边形就是这个圆的内接正n 边形.利用这一关系可以判定一个多边形是否是正多边形或作出一个正多边形．这个圆是这个正多边形的外接圆.正多边形的外接圆的圆心叫做这个正多边形的中心．外接圆的半径叫做这个正多边形的半径．正多边形每一边所对的圆心角叫做正多边形的中心角．3. 对称性：①正多边形的轴对称性：正多边形都是轴对称图形，一个正n 边形共有n 条对称轴，每条对称轴都通过正n 边形的中心．②正多边形的中心对称性：边数为偶数的正多边形是中心对称图形，它的中心是对称中心． ③正多边形的旋转对称性：正多边形都是旋转对称图形，最小的旋转角等于中心角． 典型例题解析例1. 已知点P到⊙O上的点的最短距离为3cm，最长距离为5cm，则⊙O的半径为cm．例2. 已知⊙O的半径长为2cm，如果直线l上有一点P满足PO=2cm，那么直线l与⊙O的位置关系是（）A．相切B．相交C．相离或相切D．相切或相交例3. Rt△ABC中，∠C=90°，AC=5，BC=12，如果以点C为圆心，r为半径，且⊙C与斜边AB仅有一个公共点，那么半径r的取值范围是.例4. （朝阳）如图，△MBC中，∠B=90°，∠C=60°，MB=23，点A在MB上，以AB为直径作⊙O与MC相切于点D，则CD的长为（）A．2B．3C．2 D．3例5. （葫芦岛）如图，边长为a的正六边形内有一边长为a的正三角形，则SS阴影空白（）A．3 B．4 C．5 D．6例6. 如图：⊙I是Rt△ABC的内切圆，∠C=90°，AC=6，BC=8，则⊙I的半径是.例7. （锦州）已知，⊙O为∆ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE 的延长线上，且GA=GE．（1）求证：AG与⊙O相切．（2）若AC=6，AB=8，BE=3，求线段OE的长．（2）过点O作OH⊥AB，垂足为H，例8. （来宾）如图，AB为⊙O的直径，BF切⊙O于点B，AF交⊙O于点D，点C在DF上，BC交⊙O 于点E,且∠BAF=2∠CBF,CG⊥BF于点G.连接AE.(1) 直接写出AE与BC的位置关系；(2) 求证：△BCG∽△ACE ；(3) 若∠F=60°，GF=1，求⊙O得半径.巩固训练1. （青岛）直线l与半径为r的⊙O相交，且点O到直线l的距离为6，则r的取值范围是（）A．r＜6 B．r=6 C．r＞6 D．r≥62. 在⊙O中，圆心O在坐标原点上，半径为210，点P的坐标为（4，5），那么点P与⊙O的位置关系是（）A．点P在⊙O外B．点P在⊙O上C．点P在⊙O内D．不能确定3. 已知正三角形外接圆半径为3，这个正三角形的边长是（）A．2 B．3 C．4 D．54. （天津）如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心．若∠B=25°，则∠C的大小等于（）A．20°B．25°C．40°D．50°△放在每个小正方形的边长为1的网格中，点A、B、C均落在格点上，用一个圆面5. 如下图，将ABC△，能够完全覆盖这个三角形的最小圆面的半径是________．去覆盖ABC6. （曲靖）如图,正六边形ABCDEF的边长为2，则对角线AE的长是.7. （莱芜）如图，正五边形ABCDE中，连接AC、AD、CE,CE交AD于点F，连接BF,下列说法不正确的是（）A. △CDF的周长等于AD＋CDB. FC平分∠BFDC. AC2＋BF2＝4CD2D. DE2＝EF·CE8. （广安）如图，矩形ABCD的长为6，宽为3，点O1为矩形的中心，⊙O2的半径为1，O1O2⊥AB于点P，O1O2＝6，若⊙O2绕点P按顺时针方向旋转360°，在旋转过程中，⊙O2与矩形的边只有一个公共点的情况一共出现（）A．3次B．4次C．5次D．6次9. （日照）如图，在Rt△OAB中，OA=4，AB=5，点C在OA上，AC=1，⊙P的圆心P在线段BC上，且⊙P与边AB，AO都相切.若反比例函数kyx（k≠0）的图象经过圆心P，则k= ．10. （德州）如图，⊙O的直径AB为10cm，弦BC为6cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC＝PE.（1）求AC，AD的长；（2）试判断直线PC与⊙O的位置关系，并说明理由.11. （河南）如图，CD是⊙O的直径，且CD=2cm，点P为CD的延长线上一点，过点P作⊙O的切线P A、PB，切点分别为点A、B.（1）连接AC，若∠APO=30°，试证明△ACP是等腰三角形；（2）填空：①当DP= cm时，四边形AOBD是菱形；②当DP=cm时，四边形AOBP是正方形.12. （抚州）如图，在平面直角坐标系中，⊙P经过x轴上一点C，与y轴分别相交于A，B两点，连接AP 并延长分别交⊙P、x轴于点D、点E，连接DC并延长交y轴于点F，若点F的坐标为(0，1)，点D的坐标为(6，－1).(1)求证：DC＝FC.(2)判断⊙P与x轴的位置关系，并说明理由.(3)求直线AD的解析式.中考预测1. 在直角坐标平面内，点A的坐标为（1，0），点B的坐标为（a，0），圆A的半径为2．下列说法中不正确的是（）A．当a=-1时，点B在圆A上B．当a＜1时，点B在圆A内C．当a＜-1时，点B在圆A外D．当-1＜a＜3时，点B在圆A内2. 如图，△ABC的边AC与⊙O相交于C，D两点，且经过圆心O，边AB与⊙O相切，切点为B．已知∠A ＝30°，则∠C的大小是( )A．30°B．45°C．60°D．40°3. 如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为(－3, 0)，将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（）A．1 B．1或5 C．3 D．54. 如图，P为⊙O的直径BA延长线上一点，PC与⊙O相切，切点为C，点D是⊙O上一点，连接PD. 已知PC=PD=BC. 下列结论：（1）PD与⊙O相切；（2）四边形PCBD是菱形；（3）PO=AB；（4）∠PDB=120°. 其中正确的个数为（）A. 4个B. 3个C. 2个D. 1个5. ⊙O的半径为R，点O到直线l的距离为d，R，d是方程x2－4x+m=0的两根，当直线l与⊙O相切时，m的值为．6. 直角三角形的两边长分别为16和12，则此三角形的外接圆半径是．7. 已知∠BAC=45°，一动点O在射线AB上运动（点O与点A不重合），设OA=x，如果半径为1的⊙O与射线AC只有一个公共点，那么x的取值范围是．8. 如图，两圆圆心相同，大圆的弦AB与小圆相切，AB＝8，则图中阴影部分的面积是__________．(结果保留π)9. 如图，正方形ABCD的边长为2，⊙O的直径为AD，将正方形沿EC折叠，点B落在圆上的F点，则BE的长为．10. 如图，Rt△ABC中，∠ABC=90°.以AB的中点O为圆心、OA长为半径作半圆，交AC于点D.点E为BC的中点，连接DE.（1）求证：DE是该半圆的切线；（2）若∠BAC=30°，DE=2，求AD的长.11．如图，已知等腰三角形ABC的底角为30°，以BC为直径的⊙O与底边AB交于点D，过D作DE AC，垂足为E.（1）证明：DE为⊙O的切线；（2）连接OE，若BC=4，求△OEC的面积.12. 如图，AB 是⊙O 的直径，点C 在⊙O 上，与⊙O 相切， BD ∥AC ． (1)图中∠OCD ＝_______°，理由是_____________________； (2)⊙O 的半径为3，AC ＝4，求OD 的长．13. 阅读材料：已知，如图(1)，在面积为S 的△ABC 中， BC ＝a ，AC ＝b ， AB ＝c ，内切圆O 的半径为r.连接OA 、OB 、OC ，△ABC 被划分为三个小三角形． ∵r c b a r AB r AC r BC S S S S OAB OAC OBC )(21212121++=⋅+⋅+⋅=++=△△△.. ∴cb a Sr ++=2．(1)类比推理：若面积为S 的四边形ABCD 存在内切圆(与各边都相切的圆)，如图(2)，各边长分别为AB ＝a ，BC ＝b ，CD ＝c ，AD ＝d ，求四边形的内切圆半径r ；(2)理解应用：如图(3)，在等腰梯形ABCD 中，AB ∥DC ，AB ＝21，CD ＝11，AD ＝13，⊙O 1与⊙O 2分别为△ABD 与△BCD 的内切圆，设它们的半径分别为r 1和r 2，求21r r 的值.参考答案：巩固训练∵∠ODE=∠DEA=90°，∴OD∥AC,∴11313222 OCES CE DE∆=⨯⨯=⨯=.13. 【解析】 (1)连接OA 、OB 、OC 、OD. ∵AOD COD BOC AOB S S S S S △△△△+++=dr cr br ar 21212121+++=r d c b a )(21+++=。

2021中考数学一轮专题汇编：与圆有关的位置关系一、选择题1. 如图，AB为☉O的直径，BC为☉O的切线，弦AD∥OC，直线CD交BA的延长线于点E，连接BD.下列结论:①CD是☉O的切线;②CO⊥DB;③☉EDA∽△EBD;④ED·BC=BO·BE.其中正确结论的个数有()A.4个B.3个C.2个D.1个2. 如图，AB为⊙O的切线，切点为A，连接AO，BO，BO与⊙O交于点C，延长BO与⊙O交于点D，连接AD.若∠ABO＝36°，则∠ADC的度数为()A．54° B．36° C．32° D．27°3. 在平面直角坐标系中，⊙O的圆心在原点处，半径为2，则下列各点在⊙O上的是()A．(1，1) B．(－1，3)C．(－2，－1) D．(2，－2)4. 如图，在☉MBC中，∠MBC＝90°，∠C＝60°，MB＝2 3，点A在MB上，以AB为直径作⊙O与MC相切于点D，则CD的长为()A. 2B. 3 C ．2 D ．35. (2019•娄底)如图，边长为的等边的内切圆的半径为A ．1 BC ．2 D．6. 如图，已知⊙O 1，⊙O 2，⊙O 3，⊙O 4是四个半径为3的等圆，在这四个圆中，若某圆的圆心到直线l 的距离为6，则这个圆可能是()A ．⊙O 1B ．⊙O 2C ．⊙O 3D ．⊙O 47. 如图，在正三角形网格中，☉ABC的顶点都在格点上，点P ，Q ，M 是AB 与网格线的交点，则☉ABC 的外心是( )A ．点PB ．点QC ．点MD ．点N8. 已知：在☉ABC中，AB ＝AC ，求证：∠B ＜90°.下面写出了用反证法证明这个命题过程中的四个推理步骤：①因为∠B ＋∠C≥180°与三角形内角和定理相矛盾；②所以∠B ＜90°；③假设∠B≥90°；④由AB ＝AC ，得∠C ＝∠B≥90°，即∠B ＋∠C≥180°.这四个步骤正确的顺序应是( ) A ．①②③④ B ．③④②① C ．③④①②D ．④③②①ABC △二、填空题9. 如图，在平面直角坐标系中，已知C(3，4)，以点C为圆心的圆与y轴相切．点A，B在x轴上，且OA＝OB.P为⊙C上的动点，∠APB＝90°，则AB长的最大值为________．10. 如图，P A，PB是☉O的切线，A，B为切点，点C，D在☉O上.若∠P=102°，则∠A+∠C=.11. 如图1，已知☉ABC的外心为O，BC＝10，∠BAC＝60°，分别以AB，AC 为腰向三角形外作等腰直角三角形ABD与ACE，连接BE，CD交于点P，则OP长的最小值是________．12. 如图，⊙M的圆心在一次函数y＝12x＋2的图象上运动，半径为1.当⊙M与y轴相切时，点M的坐标为__________．13. 如图，已知☉ABC的内切圆⊙O与BC边相切于点D，连接OB，OD.若∠ABC ＝40°，则∠BOD的度数是________．14. 如图，以AB为直径的☉O与CE相切于点C，CE交AB的延长线于点E，直径AB=18，∠A=30°，弦CD⊥AB，垂足为点F，连接AC，OC，则下列结论正确的是.(写出所有正确结论的序号)①=;②扇形OBC的面积为π;③☉OCF∽△OEC;④若点P为线段OA上一动点，则AP·OP有最大值20.25.15. ⊙O的半径为R，点O到直线l的距离为d，R，d是关于x的方程x2－4x＋m＝0的两根，当直线l与⊙O相切时，m的值为________．16. 如图，⊙M的圆心为M(－2，2)，半径为2，直线AB过点A(0，－2)，B(2，0)，则⊙M关于y轴对称的⊙M′与直线AB的位置关系是________．三、解答题17. 如图，在☉ABC中，AB=AC，以AB为直径的☉O分别交AC，BC于点D，E，点F在AC的延长线上，且∠BAC=2∠CBF.(1)求证:BF是☉O的切线;(2)若☉O的直径为3，sin∠CBF=，求BC和BF的长.18. 2020·凉山州模拟如图，⊙O的直径AB＝10 cm，弦BC＝6 cm，∠ACB的平分线交⊙O于点D，交AB于点E，P是AB延长线上一点，且PC＝PE.(1)求证：PC是⊙O的切线；(2)求AC，AD的长．19. 如图，AB，AC分别是☉O的直径和弦，OD⊥AC于点D.过点A作☉O的切线与OD的延长线交于点P，PC，AB的延长线交于点F.(1)求证:PC是☉O的切线;(2)若∠ABC=60°，AB=10，求线段CF的长.20. 如图，在☉ABC中，AB＝6，AC＝BC＝5，以BC为直径作⊙O交AB于点D，交AC于点G，直线DF是⊙O的切线，D为切点，交CB的延长线于点E.(1)求证：DF⊥AC；(2)求CG的长.21. （2020·临沂）☉☉1O ☉☉☉☉1r ☉2O ☉☉☉☉2r .☉1O ☉☉☉☉☉12r r +☉☉☉☉☉☉☉☉☉☉☉☉12O O ☉☉☉P ☉☉☉☉☉1212O O ☉☉☉☉☉☉☉☉☉☉☉☉☉A ☉☉☉1O A ☉2O A ☉1O A ☉1O ☉☉B ☉☉☉B ☉2O A ☉☉☉☉BC ☉12O O ☉☉C .☉1☉☉☉☉BC ☉2O ☉☉☉☉☉2☉☉12r =☉21r =☉126O O =☉☉☉☉☉☉☉☉☉.2021中考数学 一轮专题汇编：与圆有关的位置关系-答案一、选择题1. 【答案】A [解析]连接DO ，∵AD ∥OC ， ∴∠DAO=∠COB ，∠ADO=∠DOC ，∵OA=OD ，∴∠OAD=∠ODA ， ∴∠COB=∠COD ，∴☉COD≌△COB，∴∠ODC=∠OBC，∵BC为☉O的切线，∴∠OBC=90°，∴∠ODC=90°，∴CD是☉O的切线，故①正确;∵OB=OD，∠COB=∠COD，∴CO⊥DB，故②正确;∵∠EDA+∠ADO=90°，∠DBA+∠DAO=90°，∴∠EDA=∠DBA，∴☉EDA∽△EBD，故③正确;∵☉EDA∽△EBD，∴=，易证☉COB∽△BAD，∴=，∴=，∴=，即ED·BC=BO·BE，故④正确.因此本题选A.2. 【答案】D[解析] ∵AB为⊙O的切线，∴∠OAB＝90°.∵∠ABO＝36°，∴∠AOB＝90°－∠ABO＝54°.∴∠ADC＝12∠AOB＝27°.故选D.3. 【答案】B[解析] A项，点(1，1)到圆心的距离是2，2＜2，故在圆内；B 项，点(－1，3)到圆心的距离为2，2＝2，故在圆上；C项，点(－2，－1)到圆心的距离为5，5＞2，故在圆外；D项，点(2，－2)到圆心的距离为2 2，2 2＞2，故在圆外．故选B.4. 【答案】C[解析] 在Rt☉BCM中，∠MBC＝90°，∠C＝60°，∴∠BMC＝30°，∴BC＝12MC，即MC＝2BC.由勾股定理，得MC2＝BC2＋MB2.∵MB＝2 3，∴(2BC)2＝BC2＋12，∴BC ＝2.∵AB 为⊙O 的直径，且AB ⊥BC ，∴BC 为⊙O 的切线．又∵CD 也为⊙O 的切线，∴CD ＝BC ＝2.5. 【答案】A【解析】设的内心为O ，连接AO 、BO ，CO 的延长线交AB 于H ，如图，∵为等边三角形，∴CH 平分，AO 平分，∵为等边三角形， ∴，，∴，， 在中，∵，∴， 即内切圆的半径为1．故选A ．6. 【答案】B7. 【答案】B[解析] 由题意可知∠BCN ＝60°，∠ACN ＝30°，∴∠ACB ＝∠ACN ＋∠BCN ＝90°， ∴△ABC 是直角三角形，∴△ABC 的外心是斜边AB 的中点． ∵Q 是AB 的中点， ∴△ABC 的外心是点Q .8. 【答案】C二、填空题9. 【答案】16ABC△ABC △BCA ∠BCA ∠ABC △60CAB ∠=︒CH AB ⊥30OAH ∠=︒12AH BH AB ===Rt AOH △tan tan 30OH OAH AH ∠==︒1OH ==ABC△10. 【答案】219° [解析]连接AB ，∵P A ，PB 是☉O 的切线， ∴P A=PB. ∵∠P=102°，∴∠P AB=∠PBA=(180°-102°)=39°. ∵∠DAB +∠C=180°，∴∠P AD +∠C=∠P AB +∠DAB +∠C=180°+39°=219°.11. 【答案】5－533 [解析] ∵∠BAD ＝∠CAE ＝90°，∴∠DAC ＝∠BAE .在☉DAC 和☉BAE 中，⎩⎨⎧AD ＝AB ，∠DAC ＝∠BAE ，AC ＝AE ，∴△DAC ≌△BAE (SAS)， ∴∠ADC ＝∠ABE ，从而∠PDB ＋∠PBD ＝90°， 即∠DPB ＝90°，从而∠BPC ＝90°， ∴点P 在以BC 为直径的圆上．如图，过点O 作OH ⊥BC 于点H ，连接OB ，OC . ∵△ABC 的外心为O ，∠BAC ＝60°， ∴∠BOC ＝120°.又∵BC ＝10， ∴OH ＝53 3，∴OP 长的最小值是5－533.12. 【答案】(1，52)或(－1，32) [解析] ∵⊙M 的圆心在一次函数y ＝12x ＋2的图象上运动，∴设当⊙M 与y 轴相切时圆心M 的坐标为(x ，12x ＋2)．∵⊙M 的半径为1，∴x ＝1或x ＝－1，当x ＝1时，y ＝52，当x ＝－1时，y ＝32.∴点M 的坐标为(1，52)或(－1，32)．13. 【答案】70°[解析] 由切线长定理可知∠OBD ＝12∠ABC ＝20°.∵BC 是⊙O的切线，∴OD ⊥BC ，∴∠BOD ＝90°－∠OBD ＝70°.14. 【答案】①③④[解析]∵AB 是☉O 的直径，CD ⊥AB ， ∴=，故①正确.∵∠A=30°， ∴∠COB=60°， ∴扇形OBC 的面积=·π·2=π，故②错误.∵CE 是☉O 的切线， ∴∠OCE=90°，∴∠OCE=∠OFC ，又∵∠EOC=∠COF ， ∴△OCF ∽△OEC ，故③正确. 设AP=x ，则OP=9-x ， ∴AP ·OP=x (9-x )=-x 2+9x=-x -2+，∴当x=时，AP ·OP 取最大值， =20.25，故④正确. 故答案为①③④.15. 【答案】4[解析] ∵R ，d 是关于x 的方程x2－4x ＋m ＝0的两根，且直线l与⊙O 相切，∴d＝R，∴方程有两个相等的实数根，即Δ＝16－4m＝0，解得m＝4.16. 【答案】相交[解析] ∵⊙M的圆心为M(－2，2)，则⊙M关于y轴对称的⊙M′的圆心为M′(2，2)．因为M′B＝2>点M′到直线AB的距离，所以直线AB与⊙M′相交．三、解答题17. 【答案】解:(1)证明:连接AE，∵AB为直径，∴∠AEB=90°，∴AE⊥BC.∵AB=AC，∴BE=EC，∠BAE=∠CAE.∵∠BAC=2∠CBF，∴∠BAE=∠CBF.∵∠BAE+∠ABE=90°，∴∠CBF+∠ABE=90°，∴AB⊥BF，∴BF是☉O的切线.(2)由(1)得∠BAE=∠CBF，∴sin∠CBF=sin∠BAE=，∵∠AEB=90°，AB=3，∴BE=AB sin∠BAE=，∴BC=2BE=2.过点C作CH⊥BF于H点，在Rt☉CBH中，CH=BC sin∠CBF=2，BH=2，∵CH⊥BF，AB⊥BF，∴AB∥CH，∴☉FCH∽△F AB，∴=，∴=，∴BF=6.18. 【答案】解：(1)证明：连接OC，如图所示．∵AB是⊙O的直径，∴∠ACB＝90°.∵CD平分∠ACB，∴∠ACD＝∠BCD＝45°.∵PC＝PE，∴∠PCE＝∠PEC.∵∠PEC＝∠EAC＋∠ACE＝∠EAC＋45°，而∠EAC＝90°－∠ABC，∠ABC＝∠OCB，∴∠PCE＝90°－∠OCB＋45°＝90°－(∠OCE＋45°)＋45°，∴∠OCE＋∠PCE＝90°，即∠PCO＝90°，∴OC⊥PC，∴PC为⊙O的切线．(2)连接BD，如图所示．在Rt△ACB中，AB＝10 cm，BC＝6 cm，∴AC＝AB2－BC2＝102－62＝8(cm)．∵∠ACD＝∠BCD＝45°，∴∠DAB＝∠DBA＝45°，∴△ADB为等腰直角三角形，∴AD＝22AB＝5 2(cm)．19. 【答案】解:(1)证明:连接OC，∵OD⊥AC，OD经过圆心O，∴AD=CD，∴P A=PC.在△OAP和△OCP中，∴△OAP≌△OCP(SSS)，∴∠OCP=∠OAP.∵P A是☉O的切线，∴∠OAP=90°.∴∠OCP=90°，即OC⊥PC，∴PC是☉O的切线.(2)∵OB=OC，∠OBC=60°，∴△OBC是等边三角形，∴∠COB=60°，∵AB=10，∴OC=5，由(1)知∠OCF=90°，∴CF=OC tan∠COB=5.20. 【答案】解：(1)证明：如图，连接OD.∵DF 是⊙O 的切线，∴OD ⊥DF.∵AC ＝BC ，∴∠DBC ＝∠A.∵OD ＝OB ，∴∠DBC ＝∠ODB ，∴∠A ＝∠ODB ，∴OD ∥AC ，∴DF ⊥AC.(2)如图，连接CD ，BG.∵BC 是⊙O 的直径，∴∠BGC ＝∠BDC ＝90°.∵AC ＝BC ，AB ＝6，∴AD ＝BD ＝12AB ＝3.在Rt☉ACD 中，CD ＝AC2－AD2＝52－32＝4.∵AB·CD ＝2S☉ABC ＝AC·BG ，∴BG ＝AB·CD AC ＝6×45＝245，∴CG ＝BC2－BG2＝52－（245）2＝75.21. 【答案】 证明：（1）连接AP ，过点2O 作直线BC 的垂线，垂足为点M ，如下图：∵线段12O O 的中点是点P ，以1212O O 的长为半径画弧∴121212O P O P AP O O === ∴∠PAO1＝∠PO1A ，∠PAO2＝∠PO2A ，∴∠O1A O2=∠PAO1+∠PAO2＝90°∴△O1A O2是直角三角形∵2O A BC ∴∠O1A O2=∠ABC ＝90°又∵∠O2MB=90°∴四边形ABM O2是平行四边形∴O2M ＝AB= O1A －O1B=2r ∴BC 是2O 的切线；（2）∵12r =，21r =，126O O =， ∴O1A =123r r +=又∵∠O1A O2=90°∴cos ∠A O1 O2=1123162O A O O ==∴∠A O1 O2=60° 在Rt △B O1 C中：1tan602BC BO =⨯==M设O1 O2与1O 的交点为点N ，则阴影部分的面积为：11216022==223603BO C BO N S S S ππ⨯-⨯⨯=阴影扇形.【解析】（1）证切线常用的方法有“作垂线证半径”和“作半径证垂直” ，考虑到题目中的已知条件，用“作垂线证半径”更简便一些，为此我们可以过点2O 作直线BC 的垂线，垂足为点M ；同时考虑到∠O1A O2可能是直角，可以连接AP 用等腰三角形的等角对等边和三角形内角和定理进行证明；条件中还给出了平行线，因此可以证明∠ABC ＝90°，则四边形ABM O2是平行四边形，最后证明O2M ＝AB= O1A －O1B=2r ，问题得以解决.（2）求阴影部分的面积，可以根据割补法来求.解决问题的关键是分别求出△BO1C 和扇形BO1N 的面积，根据已知条件，可以先求出O1A =123r r +=，然后根据三角函数求出 ∠A O1 O2的度数，需要的数据再通过三角函数求出，问题得解.NM。

2.19 与圆有关的位置关系一、点与圆的位置关系1、设圆的半径为r，点到圆心的距离为d，则（1）点在圆内⇔d r<；（2）点在圆上⇔d r=；（3）点在圆外⇔d r>；2、不在同一条直线上的三个点确定一个圆.3、经过三角形的三个顶点可以作一个圆，这个圆叫做三角形的外接圆. 外接圆的圆心是三角形三条边的垂直平分线的交点，叫做这个三角形的外心.二、直线与圆的位置关系1、设圆的半径为r，圆心到直线的距离为d，则（1）直线与圆相交（图1）⇔d r<⇔有两个交点；（2）直线与圆相切（图2）⇔d r=⇔有一个交点；（3）直线与圆相离（图3）⇔d r>⇔无交点；2、相关概念：（1）直线和圆有两个公共点，这时我们说这条直线和圆相交，这条直线叫做圆的割线.（2）直线和圆有一个公共点，这时我们说这条直线和圆相切，这条直线叫做圆的切线，这个点叫做切点.（3）直线和圆没有公共点，这时我们说这条直线和圆相离，（4）切线长：经过圆外一点的圆切线上，这点和圆的切点之间的线段的长，叫做这点到圆的切线长.（5）与三角形三边都相切的圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.3、相关定理：知识回顾（1）切线的判定定理：经过半径外端且垂直于半径的直线是圆的切线. （2）切线的性质定理：圆的切线垂直于过切点的半径； 推论1：过圆心垂直于切线的直线必过切点； 推论2：过切点垂直于切线的直线必过圆心.以上三个定理及推论也称二推一定理：即：①过圆心；②过切点；③垂直切线，三个条件中知道其中两个条件就能推出最后一个.（3）切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.三、圆和圆的位置关系1、设两圆的半径分别为R 、r （R >r ），圆心距为d ，则（1）两圆外离（图1）⇔d R r >+⇒无交点；（2）两圆外切（图2）⇔d R r =+⇒有一个交点；（3）两圆相交（图3）⇔d R r R r -<<+⇔有两个交点；（4）两圆内切（图4）⇔d R r =-⇒ 有一个交点；（5）两圆内含（图5）⇔d R r <-⇒无交点；2、相关概念：（1）如果两个圆没有公共点，那么这两个圆相离，分为外离（图1）和内含（图5）两种情况；（2）如果两个圆只有一个公共点，那么这两个圆相切，分为外切（图2）和内切（图4）两种情况；（3）如果两个圆有两个公共点，那么这两个圆相交.考点一：点与圆的位置关系考点精讲O的半径为5cm，点P到圆心O的距离OP=6cm，则点P（）A.在⊙O外B.在⊙O上C.在⊙O内D.不能确定【答案】A【解析】解：∵OP=6cm＞5cm，∴点P在⊙O外．故选A．【点评】利用点与圆的位置关系的判断方法求解．变式跟进1如图，△ABC中，∠C=90°，AB=5，AC=4，且点D，E分别是AC，AB的中点，若作半径为3的⊙C，则下列选项中的点在⊙C外的是（）A.点BB.点DC.点ED.点A【答案】D【解析】解：∵∠C=90°，AB=5，AC=4，∴BC=3，∵且点D，E分别是AC，AB的中点，∴CD=2，CE= 52，∴点B在⊙C上，∴点E在⊙C内，∵BC=3，∴点D在⊙C内，∴点A在⊙C外，故选：D．【点评】分别求出AC、CE、BC、CD的长，根据点与圆的位置关系的判断方法进行判断即可．考点二：确定圆的条件AB的垂直平分线交弧AB于点C，交弦AB于点D．已知：A B=24cm，CD=8cm．例1例2（1）求作此残片所在的圆（不写作法，保留作图痕迹）；（2）求（1）中所作圆的半径．【答案】答案见解析【解析】（1）解：作弦AC的垂直平分线与弦AB的垂直平分线交于O点，以O为圆心OA 长为半径作圆O就是此残片所在的圆，如图．（2）解：连接OA，设OA=x，AD=12cm，OD=（x﹣8）cm，则根据勾股定理列方程：x2=122+（x﹣8）2，解得：x=13．答：圆的半径为13cm．【点评】（1）根据垂径定理作图即可。