下载文档原格式
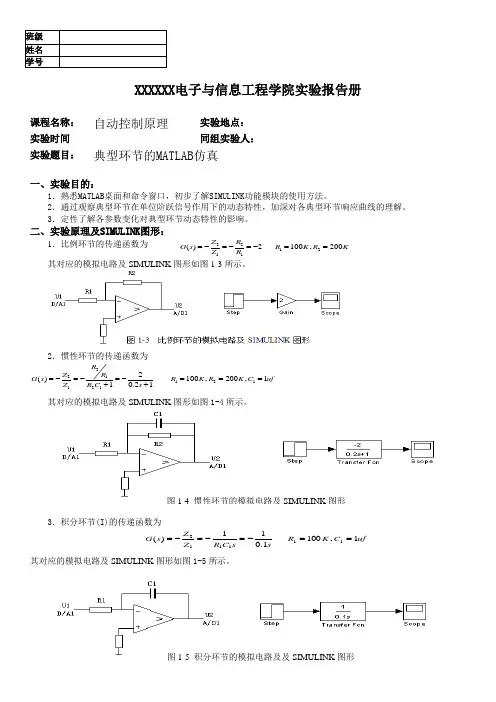
班级 姓名 学号XXXXXX 电子与信息工程学院实验报告册课程名称：自动控制原理 实验地点： 实验时间同组实验人： 实验题目： 典型环节的MATLAB 仿真一、实验目的：1．熟悉MATLAB 桌面和命令窗口，初步了解SIMULINK 功能模块的使用方法。
2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。
3．定性了解各参数变化对典型环节动态特性的影响。
二、实验原理及SIMULINK 图形：1．比例环节的传递函数为 221211()2100,200Z R G s R K R K Z R =-=-=-==其对应的模拟电路及SIMULINK 图形如图1-3所示。
2．惯性环节的传递函数为2211211212()100,200,110.21R Z R G s R K R K C uf Z R C s =-=-=-===++其对应的模拟电路及SIMULINK 图形如图1-4所示。
3．积分环节(I)的传递函数为uf C K R s s C R Z Z s G 1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK 图形如图1-5所示。
图1-5 积分环节的模拟电路及及SIMULINK 图形 图1-4 惯性环节的模拟电路及SIMULINK 图形4．微分环节(D)的传递函数为uf C K R s s C R Z Z s G 10,100)(111112==-=-=-= uf C C 01.012=<<其对应的模拟电路及SIMULINK 图形如图1-6所示。
5．比例+微分环节（PD ）的传递函数为)11.0()1()(111212+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<=== 其对应的模拟电路及SIMULINK 图形如图1-7所示。
6．比例+积分环节（PI ）的传递函数为)11(1)(11212s R s C R Z Z s G +-=+-=-= uf C K R R 10,100121===其对应的模拟电路及SIMULINK 图形如图1-8所示。
控制系统的典型环节的模拟实验报告一、实验题目：控制系统的典型环节的模拟实验报告二、实验目的：1. 了解控制系统中的典型环节的特性；2. 学习如何模拟典型环节的动态响应；3. 分析和验证控制系统的稳态和动态特性。
三、实验设备和材料：计算机、MATLAB软件、控制系统模拟工具箱。
四、实验原理：控制系统在工程实践中常常包括传感器、执行器、控制器以及被控对象等多个环节。
典型环节主要包括惯性环节和一阶滞后环节。
1. 惯性环节：惯性环节指的是一种动态响应特性，常用一阶惯性环节来描述。
其传递函数表达式为：G(s) = K / (Ts + 1)，其中K为增益，T为时间常数。
2. 一阶滞后环节：一阶滞后环节指的是一种静态响应特性，常用一阶滞后环节来描述。
其传递函数表达式为：G(s) = Ke^(-To s) / (Ts + 1)，其中K为增益，To为滞后时间常数，T为时间常数。
五、实验步骤：1. 打开MATLAB软件，并导入控制系统模拟工具箱；2. 定义惯性环节的传递函数：G1 = tf([K],[T 1]);3. 定义一阶滞后环节的传递函数：G2 = tf([K*exp(-To)],[T 1]);4. 绘制惯性环节的阶跃响应曲线：step(G1);5. 绘制一阶滞后环节的阶跃响应曲线：step(G2);6. 根据实验结果，分析和比较两种环节的动态响应特性。
六、实验结果：1. 惯性环节的阶跃响应曲线呈现一定的超调和过渡时间，随着时间的增加逐渐趋于稳态；2. 一阶滞后环节的阶跃响应曲线较为平滑，没有显著的超调和过渡时间现象，但需要较长的调节时间才能达到稳态。
七、实验结论：控制系统中的典型环节具有不同的响应特性，惯性环节一般具有超调和过渡时间现象，而一阶滞后环节则响应相对平滑。
在实际应用中，可以根据具体的控制要求和实际环境选择适合的环节类型，以达到理想的控制效果。
八、实验心得：通过本次实验，我进一步了解了控制系统中的典型环节，学会了如何模拟和分析这些环节的特性。
实验1 控制系统典型环节的模拟实验（一）实验目的：1．掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2．测量典型环节的阶跃响应曲线，了解参数变化对环节输出性能的影响。
实验原理：控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。
实验内容及步骤实验内容：观测比例、惯性和积分环节的阶跃响应曲线。
实验步骤：分别按比例，惯性和积分实验电路原理图连线，完成相关参数设置，运行。
①按各典型环节的模拟电路图将线接好(先接比例)。
(PID先不接)②将模拟电路输入端(U i)与阶跃信号的输出端Y相连接；模拟电路的输出端(Uo)接至示波器。
③按下按钮(或松开按钮)SP时，用示波器观测输出端的实际响应曲线Uo(t)，且将结果记下。
改变比例参数，重新观测结果。
④同理得积分和惯性环节的实际响应曲线，它们的理想曲线和实际响应曲线。
实验数据实验二控制系统典型环节的模拟实验（二）实验目的1．掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2．测量典型环节的阶跃响应曲线，了解参数变化对环节输出性能的影响。
实验仪器1．自动控制系统实验箱一台2．计算机一台实验原理控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。
实验内容及步骤内容：观测PI，PD和PID环节的阶跃响应曲线。
步骤：分别按PI，PD和PID实验电路原理图连线，完成相关参数设置，运行①按各典型环节的模拟电路图将线接好。
MATLAB的使用与典型环节的时域特性一. 实验目的1．MA TLAB的使用2．观察和分析各典型环节的阶跃响应曲线，了解各项电路参数对典型环节动态特性的影响二．实验原理及说明典型环节的结构图及传递函数三．实验内容及步骤观察和分析各典型环节的阶跃响应曲线，了解各项电路参数对典型环节动态特性的影响.。
系统的时域特性一. 实验目的3．观察和分析各典型环节的阶跃响应曲线，了解各项电路参数对典型环节动态特性的影响4．研究Ⅰ型二阶闭环系统的结构参数--无阻尼振荡频率ωn、阻尼比ξ对过渡过程的影响。
5． 掌握欠阻尼Ⅰ型二阶闭环系统在阶跃信号输入时的动态性能指标σ％、t p 、t s 的计算。
6． 观察和分析Ⅰ型二阶闭环系统在欠阻尼，临界阻尼，过阻尼的瞬态响应曲线，及在阶跃信号输入时的动态性能指标σ％、t p 值，并与理论计算值作比对。
二．实验原理及说明典型环节的结构图及传递函数图 典型Ⅰ型二阶单位反馈闭环系统Ⅰ型二阶系统的开环传递函数：)1()(+=TS TiS K S G Ⅰ型二阶系统的闭环传递函数标准式：2222)(1)()(nn n S S S G S G s ωξωωφ++=+= 自然频率（无阻尼振荡频率）：T iT K =n ω 阻尼比：KT Ti 21=ξKS S K S S s n n n 1010102)(2222++=++=ωξωωφ 阻尼比和开环增益K 的关系式为：临界阻尼响应：ξ=1，K=2.5，欠阻尼响应：0<ξ<1 ， K=25 ξ=0.316 过阻尼响应：ξ>1， K=1.43ξ=1.32>1计算欠阻尼二阶闭环系统在阶跃信号输入时的动态指标σ％、t p 、t s ：（K=25、ξ=0.316、n ω=15.8）超调量 ：%1.35%100%21=⨯=--eξξπσ 峰值时间：调节时间 ：6.03==ns t ξω三．实验内容及步骤观察和分析各典型环节的阶跃响应曲线，了解各项电路参数对典型环节动态特性的影响.。
自动实验一——典型环节的MATLAB仿真报告引言：典型环节的MATLAB仿真是一种常见的模拟实验方法，通过使用MATLAB软件进行建模和仿真，可以有效地研究和分析各种复杂的物理系统和控制系统。
本报告将介绍一个典型环节的MATLAB仿真实验，包括实验目的、实验原理、实验步骤、实验结果和讨论等内容。
一、实验目的本实验旨在通过MATLAB仿真实验，研究和分析一个典型环节的动态特性，深入了解其响应规律和控制方法，为实际系统的设计和优化提供理论支持。
二、实验原理典型环节是控制系统中的重要组成部分，一般包括惯性环节、惯性耦合和纯滞后等。
在本实验中，我们将重点研究一个惯性环节。
惯性环节是一种常见的动态系统，其特点是系统具有自身的动态惯性，对输入信号的响应具有一定的滞后效应，并且在输入信号发生变化时有一定的惯性。
三、实验步骤1.建立典型环节的数学模型。
根据实际情况，我们可以选择不同的数学模型描述典型环节的动态特性。
在本实验中，我们选择使用一阶惯性环节的传递函数模型进行仿真。
2.编写MATLAB程序进行仿真。
利用MATLAB软件的控制系统工具箱，我们可以方便地建立惯性环节的模型，并利用系统仿真和分析工具进行仿真实验和结果分析。
3.进行仿真实验。
选择合适的输入信号和参数设置，进行仿真实验，并记录仿真结果。
4.分析实验结果。
根据仿真结果，可以分析典型环节的动态响应特性，比较不同输入信号和控制方法对系统响应的影响。
四、实验结果和讨论通过以上步骤，我们成功地完成了典型环节的MATLAB仿真实验，并获得了仿真结果。
通过对仿真结果的分析，我们可以得到以下结论：1.惯性环节的响应规律。
惯性环节的响应具有一定的滞后效应，并且对输入信号的变化具有一定的惯性。
随着输入信号的变化速度增加，惯性环节的响应时间呈指数级减小。
2.稳态误差与控制增益的关系。
控制增益对稳态误差有重要影响，适当调整控制增益可以减小稳态误差。
3.不同输入信号的影响。
实验一 典型环节的MATLAB 仿真 一、实验目的1．熟悉MATLAB 桌面和命令窗口，初步了解SIMULINK 功能模块的使用方法。
2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。
3．定性了解各参数变化对典型环节动态特性的影响。
二、实验内容① 比例环节1)(1=s G 和2)(1=s G ；Simulink 图形实现：示波器显示结果：② 惯性环节11)(1+=s s G 和15.01)(2+=s s GSimulink 图形实现：示波器显示结果：③ 积分环节s s G 1)(1Simulink 图形实现：示波器显示结果：④ 微分环节s s G )(1Simulink 图形实现：波器显示结果：⑤ 比例+微分环节（PD ）2)(1+=s s G 和1)(2+=s s G1）、G1（s ）=s+2Simulink 图形实现：示波器显示结果：2）、G2（s）=s+1 Simulink图形实现：示波器显示结果：⑥ 比例+积分环节（PI ）s s G 11)(1+=和s s G 211)(2+=1）、G1（1）=1+1/sSimulink 图形实现：示波器显示结果：2）G2（s）=1+1/2s Simulink图形实现：示波器显示结果：三、心得体会通过这次实验我学到了很多，对课本内容加深了理解，熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法，加深对各典型环节响应曲线的理解，这为对课程的学习打下了一定基础。
实验二线性系统时域响应分析一、实验目的1．熟练掌握step( )函数和impulse( )函数的使用方法，研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。
2．通过响应曲线观测特征参量ζ和nω对二阶系统性能的影响。
3．熟练掌握系统的稳定性的判断方法。
二、实验内容1．观察函数step( )的调用格式，假设系统的传递函数模型为243237()4641s s G s s s s s ++=++++绘制出系统的阶跃响应曲线？2．对典型二阶系统222()2n n n G s s s ωζωω=++1）分别绘出2(/)n rad s ω=，ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线，分析参数ζ对系统的影响，并计算ζ=0.25时的时域性能指标,,,,p r p s ss t t t e σ。
实验一典型环节的MATLAB仿真Experiment 1 MATLAB simulation of typical link一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。
2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。
3．定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型，进行仿真和调试。
1．运行MATLAB软件，在命令窗口栏“>>”提示符下键入simulink命令，按Enter 键或在工具栏单击按钮，即可进入如图1-1所示的SIMULINK仿真环境下。
2．选择File菜单下New下的Model命令，新建一个simulink仿真环境常规模板。
3．在simulink仿真环境下，创建所需要的系统。
以图1-2所示的系统为例，说明基本设计步骤如下：1）进入线性系统模块库，构建传递函数。
点击simulink下的“Continuous”，再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。
2）改变模块参数。
在simulink仿真环境“untitled”窗口中双击该图标，即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数，数字之间用空格隔开；设置完成后，选择OK，即完成该模块的设置。
3）建立其它传递函数模块。
按照上述方法，在不同的simulink的模块库中，建立系统所需的传递函数模块。
例：比例环节用“Math”右边窗口“Gain”的图标。
4）选取阶跃信号输入函数。
用鼠标点击simulink下的“Source”，将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口，形成一个阶跃函数输入模块。
