实验一典型环节的MATLAB仿真

实验一 MATLAB 及仿真实验（控制系统的时域分析）一、实验目的学习利用MATLAB 进行控制系统时域分析，包括典型响应、判断系统稳定性和分析系统的动态特性；二、预习要点1、 系统的典型响应有哪些？2、 如何判断系统稳定性？3、 系统的动态性能指标有哪些？三、实验方法（一） 四种典型响应1、 阶跃响应：阶跃响应常用格式：1、)(sys step ；其中sys 可以为连续系统，也可为离散系统。

2、),(Tn sys step ；表示时间范围0---Tn 。

3、),(T sys step ；表示时间范围向量T 指定。

4、),(T sys step Y =；可详细了解某段时间的输入、输出情况。

2、 脉冲响应：脉冲函数在数学上的精确定义：0,0)(1)(0〉==⎰∞t x f dx x f 其拉氏变换为：)()()()(1)(s G s f s G s Y s f === 所以脉冲响应即为传函的反拉氏变换。

脉冲响应函数常用格式： ① )(sys impulse ；② );,();,(T sys impulse Tn sys impulse ③ ),(T sys impulse Y =（二） 分析系统稳定性有以下三种方法：1、 利用pzmap 绘制连续系统的零极点图；2、 利用tf2zp 求出系统零极点；3、 利用roots 求分母多项式的根来确定系统的极点（三） 系统的动态特性分析Matlab 提供了求取连续系统的单位阶跃响应函数step 、单位脉冲响应函数impulse 、零输入响应函数initial 以及任意输入下的仿真函数lsim.四、实验内容(一) 稳定性1.系统传函为()27243645232345234+++++++++=s s s s s s s s s s G ，试判断其稳定性%Matlab 计算程序num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den) 2.用Matlab 求出253722)(2342++++++=s s s s s s s G 的极点。

自动控制原理实验报告实验名称：班级：姓名：学号：实验一典型环节的模拟研究一、实验目的1、学习典型环节模拟电路，通过搭建典型环节模拟电路，熟悉并掌握自动控制实验箱的使用方法。

2、掌握典型环节的matlab软件仿真方法。

3、了解并掌握各典型环节的传递函数及其特性，观察和分析个典型环节的响应曲线。

二、实验内容1、构成个典型环节模拟电路，计算传递函数，明确各参数物理意义2、用Matlab软件仿真个典型环节的阶跃响应，分析其性能。

3、在自控实验箱中搭建个典型环节的模拟电路，调节模拟电路参数，观测并记录各环节的阶跃响应曲线，研究参数变化对典型环节阶跃响应的影响。

4、将软件仿真结果与模拟电路观测的结果作比较。

三、实验步骤1、构成典型环节模拟电路（1）比例环节传递函数为：G（s）=K=R2/R1，R1=200K, R2=100K或R2=200K（2）积分环节传递函数为：G（s）=1/(T*s),T=R1*C1，R1=200K，C1=1.0uF或2.0uF（3）比例积分环节传递函数为：G（s）=K+1/(T*s), K=R4/R3，T=R3*C1，R1=200K，C1=1.0uF或2.0uF（4）微分环节传递函数为：G（s）=Ts，T=R2*C1，R2=100K，C1 =0.1uF（5）比例微分环节传递函数为：G（s）=K+Ts，K=R2/R1，T=R2*C1，R2=100K，C1 =0.1uF（6）惯性环节传递函数为：G（s）=K/(Ts+1)，K=R2/R1，T=R2*C1，C1=1.0uF或2.0uF2、用Matlab软件仿真实现各典型环节阶跃响应，并保存不同参数下各环节的阶跃响应曲线；（1）比例环节R2=200K：g=tf(200,200);step(g)R2=100K：g=tf(100,200);step(g)（2）积分环节C1=1.0uF：g=tf(1,[0.2 ,0]);step(g), axis([0 1 0 5])C1=2.0uF：g=tf(1,[0.4,0]);step(g), axis([0 1 0 2.5])（3）比例积分环节C1=1.0uF：g=tf([0.2,1],[0.2,0]);step(g), axis([0 1 0 10.5])C1=2.0uF：g=tf([0.4,1],[0.4,0]);step(g), axis([0 1 0 5.5])（4）微分环节不能用step（）函数，用Simulink仿真（5）比例加微分环节不能用step（）函数，用Simulink仿真R1=20KR1=100K（6）惯性环节C1=1.0uFg=tf(1,[0.2,1]);step(g)C2=2.0uFg=tf(1,[0.4,1]);step(g)3、在自控实验箱中搭建各环节模拟电路，观测并记录个典型环节阶跃响应曲线，调整参数，重复进行。

自动实验一——典型环节的MATLAB仿真报告引言：典型环节的MATLAB仿真是一种常见的模拟实验方法，通过使用MATLAB软件进行建模和仿真，可以有效地研究和分析各种复杂的物理系统和控制系统。

本报告将介绍一个典型环节的MATLAB仿真实验，包括实验目的、实验原理、实验步骤、实验结果和讨论等内容。

一、实验目的本实验旨在通过MATLAB仿真实验，研究和分析一个典型环节的动态特性，深入了解其响应规律和控制方法，为实际系统的设计和优化提供理论支持。

二、实验原理典型环节是控制系统中的重要组成部分，一般包括惯性环节、惯性耦合和纯滞后等。

在本实验中，我们将重点研究一个惯性环节。

惯性环节是一种常见的动态系统，其特点是系统具有自身的动态惯性，对输入信号的响应具有一定的滞后效应，并且在输入信号发生变化时有一定的惯性。

三、实验步骤1.建立典型环节的数学模型。

根据实际情况，我们可以选择不同的数学模型描述典型环节的动态特性。

在本实验中，我们选择使用一阶惯性环节的传递函数模型进行仿真。

2.编写MATLAB程序进行仿真。

利用MATLAB软件的控制系统工具箱，我们可以方便地建立惯性环节的模型，并利用系统仿真和分析工具进行仿真实验和结果分析。

3.进行仿真实验。

选择合适的输入信号和参数设置，进行仿真实验，并记录仿真结果。

4.分析实验结果。

根据仿真结果，可以分析典型环节的动态响应特性，比较不同输入信号和控制方法对系统响应的影响。

四、实验结果和讨论通过以上步骤，我们成功地完成了典型环节的MATLAB仿真实验，并获得了仿真结果。

通过对仿真结果的分析，我们可以得到以下结论：1.惯性环节的响应规律。

惯性环节的响应具有一定的滞后效应，并且对输入信号的变化具有一定的惯性。

随着输入信号的变化速度增加，惯性环节的响应时间呈指数级减小。

2.稳态误差与控制增益的关系。

控制增益对稳态误差有重要影响，适当调整控制增益可以减小稳态误差。

3.不同输入信号的影响。

实验一典型环节的MATLAB仿真一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。

2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。

3．定性了解各参数变化对典型环节动态特性的影响。

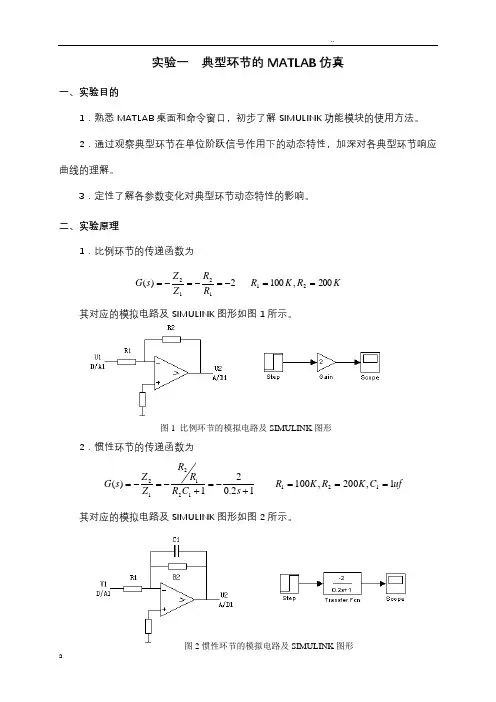
二、实验原理1．比例环节的传递函数为KRKRRRZZsG200,1002)(211212==-=-=-=其对应的模拟电路及SIMULINK图形如图1所示。

2．惯性环节的传递函数为ufCKRKRsCRRRZZsG1,200,10012.021)(121121212===+-=+-=-=其对应的模拟电路及SIMULINK图形如图2所示。

图1 比例环节的模拟电路及SIMULINK图形图2惯性环节的模拟电路及SIMULINK图形3．积分环节(I)的传递函数为ufCKRssCRZZsG1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK图形如图3所示。

4．微分环节(D)的传递函数为ufCKRssCRZZsG10,100)(111112==-=-=-=ufCC01.012=<<其对应的模拟电路及SIMULINK图形如图4所示。

5．比例+微分环节（PD）的传递函数为)11.0()1()(111212+-=+-=-=ssCRRRZZsGufCCufCKRR01.010,10012121=<<===其对应的模拟电路及SIMULINK图形如图5所示。

图3 积分环节的模拟电路及及SIMULINK图形图4 微分环节的模拟电路及及SIMULINK图形6．比例+积分环节（PI）的传递函数为)11(1)(11212sRsCRZZsG+-=+-=-=ufCKRR10,100121===其对应的模拟电路及SIMULINK图形如图6所示。

三、实验内容按下列各典型环节的传递函数，建立相应的SIMULINK仿真模型，观察并记录其单位阶跃响应波形。

实验一典型环节的MATLAB仿真Experiment 1 MATLAB simulation of typical link一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。

2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。

3．定性了解各参数变化对典型环节动态特性的影响。

二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。

利用SIMULINK功能模块可以快速的建立控制系统的模型，进行仿真和调试。

1．运行MATLAB软件，在命令窗口栏“>>”提示符下键入simulink命令，按Enter 键或在工具栏单击按钮，即可进入如图1-1所示的SIMULINK仿真环境下。

2．选择File菜单下New下的Model命令，新建一个simulink仿真环境常规模板。

3．在simulink仿真环境下，创建所需要的系统。

以图1-2所示的系统为例，说明基本设计步骤如下：1）进入线性系统模块库，构建传递函数。

点击simulink下的“Continuous”，再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。

2）改变模块参数。

在simulink仿真环境“untitled”窗口中双击该图标，即可改变传递函数。

其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数，数字之间用空格隔开；设置完成后，选择OK，即完成该模块的设置。

3）建立其它传递函数模块。

按照上述方法，在不同的simulink的模块库中，建立系统所需的传递函数模块。

例：比例环节用“Math”右边窗口“Gain”的图标。

4）选取阶跃信号输入函数。

用鼠标点击simulink下的“Source”，将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口，形成一个阶跃函数输入模块。

实验一典型环节的MATLAB仿真一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。

2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。

3．定性了解各参数变化对典型环节动态特性的影响。

二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。

利用SIMULINK功能模块可以快速的建立控制系统的模型，进行仿真和调试。

1．运行MATLAB软件，在命令窗口栏“>>”提示符下键入simulink命令，按Enter 键或在工具栏单击按钮，即可进入如图1-1所示的SIMULINK仿真环境下。

2．选择File菜单下New下的Model命令，新建一个simulink仿真环境常规模板。

3．在simulink仿真环境下，创建所需要的系统。

以图1-2所示的系统为例，说明基本设计步骤如下：1）进入线性系统模块库，构建传递函数。

点击simulink下的“Continuous”，再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。

2）改变模块参数。

在simulink仿真环境“untitled”窗口中双击该图标，即可改变传递函数。

其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数，数字之间用空格隔开；设置完成后，选择OK，即完成该模块的设置。

3）建立其它传递函数模块。

按照上述方法，在不同的simulink的模块库中，建立系统所需的传递函数模块。

例：比例环节用“Math”右边窗口“Gain”的图标。

4）选取阶跃信号输入函数。

用鼠标点击simulink下的“Source”，将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口，形成一个阶跃函数输入模块。

5）选择输出方式。

用鼠标点击simulink下的“Sinks”，就进入输出方式模块库，通常选用“Scope”的示波器图标，将其用左键拖至新建的“untitled”窗口。

利用simulink进行仿真的步骤：1.打开Matlab软件；2.在Command Window命令行>>后输入simulink并回车或点击窗口上部图标直接进入simulink界面；3.在simulink界面上点击File-New-Modle就可以在新的界面上建立系统的仿真模型了；4.在左面的器件模型库中找到所需模型，用鼠标将器件模型拖到建立的界面上，然后用鼠标将它们用连线连起来，系统的仿真模型就建立起来了；5.点击界面上部的图标‘’进行仿真，双击示波器就可以看到仿真结果。

实验要用到的元件模型的图标及解释如下：阶跃信号：在simulink-source中可以找到，双击可以设定阶跃时间。

sum：在simulink-math operations中可以找到，双击可以改变器属性以实现信号相加还是相减；比例环节：在simulink-math operations中可以找到，双击可以改变器属性以改变比例系数；积分环节：在simulink-continues中可以找到；传函的一般数学模型表达形式：在simulink-continues中可以找到，双击可以对传递函数进行更改（通过设定系数）。

示波器：在simulink-sinks中可以找到。

实验一典型环节及其阶跃响应一、实验目的1．通过观察典型环节在单位阶跃信号作用下的动态特性，熟悉各种典型环节的响应曲线。

2．定性了解各参数变化对典型环节动态特性的影响。

3．初步了解MATLAB 中SIMULINK 的使用方法。

二、SIMULINK 实例1．掌握比例、积分、一阶惯性、实际微分、比例＋微分、比例＋积分环节的动态特性。

[例题]：观察实际微分环节的动态特性（1）连接系统,如上图所示:（2）参数设置:在simulation/paramater 中将仿真时间(Stop Time )设置为10秒，用鼠标双击实际微分环节,设Kd=1,Td=1（3）仿真:simulation/start，仿真结果如图1-1所示。

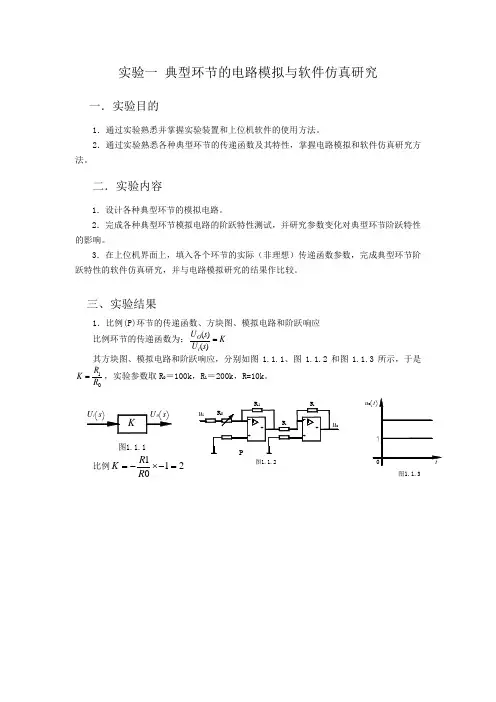
实验一典型环节的电路模拟与软件仿真研究一．实验目的1．通过实验熟悉并掌握实验装置和上位机软件的使用方法。

2．通过实验熟悉各种典型环节的传递函数及其特性，掌握电路模拟和软件仿真研究方法。

二．实验内容1．设计各种典型环节的模拟电路。

2．完成各种典型环节模拟电路的阶跃特性测试，并研究参数变化对典型环节阶跃特性的影响。

3．在上位机界面上，填入各个环节的实际（非理想）传递函数参数，完成典型环节阶跃特性的软件仿真研究，并与电路模拟研究的结果作比较。

三、实验结果积分环节的传递函数为：Tss U s U i O 1)()(=其方块图、模拟电路和阶跃响应，分别如图1.2.1、图1.2.2和图1.2.3所示，于是C R T 0=，实验参数取R 0＝100k ，C ＝1uF ，R=10k 。

4．比例微分(PD)环节的传递函数、方块图、模拟电路和阶跃响应比例微分环节的传递函数为：)1(Ts K U UiO +=其方块图和模拟电路分别如图1.4.1、图1.4.2所示。

其模拟电路是近似的（即实际PD环节）＝10k ，R 3其方块图、模拟电路和阶跃响应，分别如图1.5.1、图1.5.2和图1.5.3所示，其中C R T R R K 101,==，实验参数取R 0＝200k ，R 1＝200k ，C ＝1uF ，R=10k 。

对应理想的和实际的比例积分微分(PID)环节的阶跃响应分别如图1.6.3 a 、图1.6.3 b 所示。

实际PID 环节的传递函数为：1222110010132()1(1)()(1)o i U s R R R C R C s U s R R C s R C R C s ++=+++（供软件仿真参考）实验二 典型系统动态性能和稳定性分析一．实验目的1．学习和掌握动态性能指标的测试方法。

2．研究典型系统参数对系统动态性能和稳定性的影响。

二．实验内容1．观测二阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。