椭圆滤波器word版
- 格式:doc
- 大小:61.50 KB
- 文档页数:2

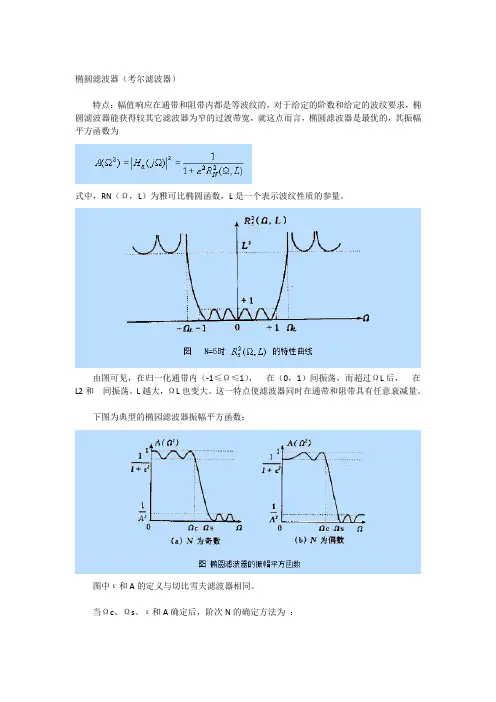
椭圆滤波器(考尔滤波器)
特点:幅值响应在通带和阻带内都是等波纹的,对于给定的阶数和给定的波纹要求,椭圆滤波器能获得较其它滤波器为窄的过渡带宽,就这点而言,椭圆滤波器是最优的,其振幅平方函数为
式中,RN(Ω,L)为雅可比椭圆函数,L是一个表示波纹性质的参量。
由图可见,在归一化通带内(-1≤Ω≤1),在(0,1)间振荡,而超过ΩL后,在L2和间振荡。
L越大,ΩL也变大。
这一特点使滤波器同时在通带和阻带具有任意衰减量。
下图为典型的椭园滤波器振幅平方函数:
图中ε和A的定义与切比雪夫滤波器相同。
当Ωc、Ωs、ε和A确定后,阶次N的确定方法为:
上面讨论了三种最常用模拟低通滤波器的特性和设计方法,设计时按照指标要求,合理选用。
一般,椭圆滤波器的阶次可最低,切比雪夫次之,巴特沃兹最高,参数的灵敏度则恰恰相反。

脉冲响应不变法设计级联型椭圆滤波器学生姓名:指导老师:摘要本课程设计的主要内容是利用脉冲响应不变法设计一个椭圆滤IIR波器,对一段含单频噪声的语音信号进行滤波去噪处理,比较滤波前后的波形和频谱并进行分析,根据结果和学过的理论得出合理的结论。
本课程设计的平台为MATLAB,用m语言进行变编程实现。
首先利用Windows下的录音机录制一段语音信号,然后在在信号中加入一个单频噪声,绘制波形并观察其频谱特点,最后设计一个满足指标的椭圆滤波器,对该含噪语音信号进行滤波去噪处理并分析。
由分析结果可知,滤波器后的语音信号与原始信号基本一致,即设计的椭圆滤波器能够去除信号中所加单频噪声,达到了设计目的。
关键词MATLAB;脉冲响应;椭圆;滤波去噪1 引言IIR(Infinite Impulse Response)数字滤波器,又名“无限脉冲响应数字滤波器”,或“递归滤波器”。
IIR滤波器设计方法依赖于已有的模拟滤波器得到数字滤波器,将这些模拟滤波器称作原型滤波器。
在实际中广泛采用三种原型滤波器,即:如巴特沃兹、切比雪夫和椭圆滤波器。
本课程设计利用的原型为椭圆滤波器。
用麦克风采集一段语音信号,并转换成格式为格式为单声道,采样速率8kHz,8位码,绘制波形并观察其频谱特点。
加入一个频率为2000Hz带外单频噪声。
用脉冲响应不变法设计一个满足指标的椭圆滤波器,对该含噪语音信号进行滤波去噪处理,比较滤波前后的波形和频谱并进行分析。
最后画出滤波器级联型结构图。
1.1课程设计的目的本课程设计的主要内容是在MATLAB软件平台下,运用学过的理论知识,用脉冲响应不变法设计一个可以滤除噪音的椭圆滤波器。
课程设计是学习中的一个重要的内容,通过此次的课程设计,可以深入理解IIR滤波器与其滤波性能,并且学会用MATLAB 进行编程、设计,实现上述指标。
在进行了专业基础课和《数字信号处理》课程学习的基础上,设计一个简单的滤波器,综合运用这些知识解决一定的实际问题,使学生在所学知识的综合运用能力上以及分析问题、解决问题能力上得到一定的提高。

The University of South China数字信号处理课程设计题目椭圆 IIR高通数字滤波器学院名称电气工程学院指导教师陈忠泽博士班级电子071班学号 20074470154学生姓名张乐2010年6月10日摘要本篇论文叙述了数字滤波器的基本原理、IIR数字滤波器的设计方法和IIR 数字高通滤波器设计在MATLAB上的实现与IIR数字滤波器在实际中的应用。
无限脉冲响应(IIR)数字滤波器是冲激响应函数)(th包含无限个抽样值的滤波器,一般是按照预定的模拟滤波器的逼近函数来转换成相应的数字滤波器,现有的逼近函数如巴特沃斯、切比雪夫。
设计IIR数字滤波器在工程上常用的有两种:脉冲响应不变法、双线性变换法。
其设计过程都是由模拟滤波器的系统函数)H去(s变换出相应的数字滤波器的系统函数)H。
(z关键词:数字滤波器;巴特沃斯;切比雪夫;双线性变换法AbstractThis paper describes the basic principles of digital filters, IIR digital filter design methods and high-pass IIR digital filter design in MATLAB Implementation and IIR digital filter in the actual application. Infinite impulse response (IIR) digital filter is the impulse response function h (t) unlimited number of sample values contained in the filter, typically analog filters according to the approximation function to convert the digital filter, the existing approximating function such as Butterworth, Chebyshev. Design of IIR digital filters commonly used in engineering, there are two: the same impulse response method, bilinear transform. Its design process by the analog filters are the system function H (s) to transform the corresponding digital filter system function H (z).Keywords: digital filters; Butterworth; Chebyshev; bilinear transform目录引言 (4)1 数字滤波器的基本原理 (4)1.1设计IIR数字滤波器主要步骤 (5)2 IIR高通滤波器的指标计算 (5)3 高通滤波器的实现结构 (8)4、IIR数字高通滤波器中有限字长的影响 (10)4.1对比结果 (13)5、椭圆IIR高通滤波(hButterwort)设计程序 (13)心得体会 (16)参考文献 (17)基于椭圆法设计IIR高通滤波器引言数字滤波器的滤波过程是一个计算过程,它将输入信号的序列数字按照预定的要求转换成输出序列。

设计椭圆低通滤波器椭圆低通滤波器滤波器设计实验(一)一.实验目的1、了解滤波器设计理论基础。
2、掌握滤波器设计软件Filter Solutions使用方法。
3、掌握无源滤波器设计及。
二.实验内容1、采用Filter Solutions设计LC 椭圆低通滤波器。
2、焊接电路并测试滤波器性能。
三.实验器材示波器、毫伏表、信号源、扫频仪。
四.实验原理(一)滤波器基本理论(二)滤波器设计方法(三)五.实验步骤1、采用Filter Solutions软件,如图1.2,对滤波器进行参数设计:filter Attributes 中设置滤波器的阶数为4、通频带频率为30KHz ,阻带截止频率为60KHz ,通带内最大起伏为1dB ;图1.2 Filter solutions 设计界面无源滤波器:1KHZ —19.2dB 27.0 KHZ —22.2dB 90 KHZ —36.0dB 60 KHZ —29.8dB滤波器设计实验(二)一.实验目的1、加深对滤波器设计参数的理解,提高滤波器性能指标。
2、熟练掌握Filter Solutions使用方法。
3、熟练掌握滤波器设计、焊接及性能测试方法。
实验内容1分别设计一个巴特沃兹、切比雪夫和椭圆有源低通滤波器。
要求截止频率为100kHz ,带外衰减不小于60dB/十倍频程,截止频率误差绝对值不大于2%,通带和阻带纹波尽可能小。
椭圆:实际测量:1 KHZ —99.14dB 97.5KHZ —12.1dB 300KHZ —46.1dB实际测量:—9.26dB 1KHZ —12.3dB 104KHZ —49.3dB 300KHZ实际测量:—9.31dB 1KHZ —12.3dB 104KHZ —44.1dB 300KHZ2、设计一个带通滤波器,阻带衰减:40dB ,中心频率:60kHZ ,通带宽度:10kHZ ,阻带宽度:60kHZ 。
实际测量: 60KHz ,0dB 66KHz ,-3.3dB 56KHz,-3.0dB3、设计一个低通滤波器,截止频率为500kHz ,带外衰减不小于40dB/十倍频程,截止频率误差绝对值不大于10%。

南华大学数字信号处理课程设计学院: 电气工程学院学生姓名:张鑫学号:20094470134专业班级:电子091设计题目:椭圆高通IIR数字滤波器设计指导老师: 陈忠泽2013年1月每位同学根据自己在班里的学号(最后两位)查表一得到一个四位数,由该四位数索引表二确定待设计数字滤波器的类型及其设计方法,然后用指定的设计方法完成滤波器设计。
要求:1. 滤波器的设计指标:(1)通带截止频率ωpc=e i d50∙0.2π rad,(2)阻带截止频率ωsc=e i d50∙0.6π rad,(3)通带最大衰减a p=1dB, (4)阻带最小衰减a s=60dB其中,—你的学号的最后两位2、题目:椭圆高通IIR数字滤波器设计(数字频率转换)3。
滤波器的初始设计通过手工计算完成;4。
在计算机辅助计算基础上分析滤波器结构对其性能指标的影响(至少选择两种以上合适的滤波器结构进行分析);5。
在计算机辅助计算基础上分析滤波器参数的字长对其性能指标的影响;6。
以上各项要有理论分析和推导、原程序以及表示计算结果的图表;7。
课程设计结束时提交设计说明书。
一手工计算完成椭圆IIR数字高通滤波器的初始设计1.设计要求滤波器的设计指标要求为(1)通带截止频率ωpc=e i d50∙0.2π rad,(2)阻带截止频率ωsc=e i d50∙0.6π rad,(3)通带最大衰减a p=1dB,(4)阻带最小衰减a s=60dB其中i d为我学号的后两位.我的学号20094470134,所以i d=34。
由此计算得:(1)通带截止频率:ωp=e i d50∙0.2π rad=e3450∙0.2π rad=1。
2407,f p= 0.1974(2)阻带截止频率:ωs=e i d50∙0.6π rad=e3450∙0.6π rad=3。
7222,f s=0.5924(3)通带最大衰减:a p=1dB,(4)阻带最小衰减:a s=60dB2.数字边界频率转换成模拟边界频率转换关系为:Ω=2T tan12ω其中,令T=2s 计算得: Ωp=0.7144 rad/sΩs=—3.3473 rad/sa p =1dB a s =60dBλ=Ωp Ωs=—0.2134为归一化基准频率的条件下,通带、阻带阶值归一化频率互为倒数。


目录1摘要 (3)2设计原理 (4)2.1 切比雪夫滤波器介绍 (4)2.2滤波器的分类 (5)2.3 模拟滤波器的设计指标 (6)3切比雪夫I型滤波器 (7)3.1 切比雪夫滤波器的设计原理 (7)3.2切比雪夫滤波器的设计步骤 (10)3.3 用matlab编程设计切比雪夫低通滤波器 (11)4 总结 (18)5 参考文献 (18)摘要随着信息和数字时代的到来,数字信号处理已成为当今一门极其重要的学科和技术领域。
在现代通信系统中,由于信号中经常混有各种复杂成分,因此很多信号的处理都是基于滤波器而进行的。
所以,数字滤波器在数字信号处理中起着举足轻重的作用。
而数字滤波器的设计都要以模拟滤波器为基础的,这是因为模拟滤波器的理论和设计方方法都已发展的相当成熟,且有典型的模拟滤波器供我们选择。
,如巴特沃思滤波器、切比雪夫滤波器等。
本次课程设计将运用MATLAB设计一个基于切比雪夫低通滤波器,并出所设计滤波器的幅度及幅度衰减特性。
关键词:滤波切比雪夫模拟低通1切比雪夫滤波器介绍在巴特沃兹滤波器中,幅度响应在通带和阻带内都是单调的。
因此,若滤波器的技术要求是用最大通带和阻带的逼近误差来给出的话,那么,在靠近通带低频端和阻带截止频率以上的部分都会超出技术指标。
一种比较有效的途径是使逼近误差均匀地分布于通带或阻带内,或同时在通带和阻带内都均匀分布,这样往往可以降低所要求的滤波器阶次。
通过选择一种具有等波纹特性而不是单调特性的逼近方法可以实现这一点。
切比雪夫型滤波器就具有这种性质:其频率响应的幅度既可以在通带中是等波纹的,而在阻带中是单调的(称为I 型切比雪夫滤波器),也可以在通带中是单调的,而在阻带中是等波纹的(称为II 型切比雪夫滤波器),其中切比雪夫II 型滤波器又称为逆切比雪夫滤波器。
I 型切比雪夫滤波器的幅度平方函数是2|)(|Ωj H C =)/(1122c N C ΩΩ+ε (2.1) 其中ε是一个小于1的正数,它与通带波纹有关,ε越大,波纹也越大,式中为N 阶切比雪夫多项式,定义为)cos cos()(1x N x C N -= (2.2) 当N 大于或等于1时,从定义切比雪夫多项式可以直接得出由)(x C N 和)(1x C N -求)(1x C N +的递推公式。

椭圆函数低通滤波器设计引言椭圆函数低通滤波器是一种常用的滤波器,在信号处理中起着重要的作用。
它具有较为复杂的设计和计算方法,但可以实现较为精确的滤波效果。
本文将介绍椭圆函数低通滤波器的设计原理和步骤,并给出具体的实例。
设计原理椭圆函数低通滤波器的设计基于椭圆函数(或称Chebyshev函数)的性质。
椭圆函数具有特殊的振幅响应特性,可以实现更为陡峭的滤波特性。
在椭圆函数低通滤波器设计中,需要指定截止频率、通带波纹和阻带衰减等参数。
通过调整这些参数,可以灵活地设计出满足特定需求的低通滤波器。
设计步骤椭圆函数低通滤波器的设计步骤如下:1.确定滤波器的截止频率。
根据具体应用需求,选择适当的截止频率。
截止频率是指滤波器开始对信号进行衰减的频率。
2.确定通带波纹和阻带衰减。
通带波纹是指通过滤波器的信号波形的最大波动幅度,阻带衰减是指滤波器对截止频率之后的频率的衰减程度。
3.根据截止频率、通带波纹和阻带衰减等参数,计算滤波器的阶数。
阶数是指滤波器的阶数,即滤波器的复杂度。
较高的阶数可以实现更陡峭的滤波特性,但也会增加滤波器的计算和设计难度。
4.根据计算的阶数,使用椭圆函数逼近方法计算椭圆函数的极点和零点。
极点和零点是滤波器设计中重要的参数,它们的位置决定了滤波器的频率响应特性。
5.根据计算得到的极点和零点,构造椭圆函数低通滤波器的传递函数。
传递函数描述了滤波器的输入输出关系。
6.对传递函数进行归一化处理,以确保滤波器的增益在通带为1。
7.根据得到的传递函数,设计数字滤波器的巴特沃斯原型。
8.使用数字滤波器设计中的双线性变换方法将巴特沃斯原型转换为数字滤波器。
实例演示以一个实例来演示椭圆函数低通滤波器的设计过程。
假设我们需要设计一个截止频率为1 kHz,通带波纹为0.5 dB,阻带衰减为40 dB的椭圆函数低通滤波器。
根据设计步骤,首先确定截止频率为1 kHz。
然后根据通带波纹和阻带衰减,选择滤波器的阶数为4。

椭圆高通IIR数字滤波器设计学院名称指导教师班级学号学生姓名2010.06一、数字滤波器数字滤波器是对数字信号实现滤波的线性时不变系统。
数字滤波实质上是一种运算过程,实现对信号的运算处理。
输入数字信号(数字序列)通过特定的运算转变为输出的数字序列,因此,数字滤波器本质上是一个完成特定运算的数字计算过程,也可以理解为是一台计算机。
描述离散系统输出与输入关系的卷积和差分方程只是给数字信号滤波器提供运算规则,使其按照这个规则完成对输入数据的处理。
时域离散系统的频域特性:,其中、分别是数字滤波器的输出序列和输入序列的频域特性(或称为频谱特性),是数字滤波器的单位取样响应的频谱,又称为数字滤波器的频域响应。
输入序列的频谱经过滤波后,因此,只要按照输入信号频谱的特点和处理信号的目的,适当选择,使得滤波后的满足设计的要求,这就是数字滤波器的滤波原理。
数字滤波器根据其冲激响应函数的时域特性,可分为两种,即无限长冲激响应(IIR)数字滤波器和有限长冲激响应(FIR)数字滤波器。
IIR 数字滤波器的特征是,具有无限持续时间冲激响应,需要用递归模型来实现,其差分方程为:系统函数为:设计IIR滤波器的任务就是寻求一个物理上可实现的系统函数H(z),使其频率响应H(z)满足所希望得到的频域指标,即符合给定的通带截止频率、阻带截止频率、通带衰减系数和阻带衰减系数。
二、数字滤波器的设计方法IIR数字滤波器是一种离散时间系统,其系统函数为假设M≤N,当M>N时,系统函数可以看作一个IIR的子系统和一个(M-N)的FIR子系统的级联。
IIR数字滤波器的设计实际上是求解滤波器的系数和,它是数学上的一种逼近问题,即在规定意义上(通常采用最小均方误差准则)去逼近系统的特性。
如果在S 平面上去逼近,就得到模拟滤波器;如果在z 平面上去逼近,就得到数字滤波器。
1.用脉冲相应不变法设计IIR 数字滤波器利用模拟滤波器来设计数字滤波器,也就是使数字滤波器能模仿模拟滤波器的特性,这种模仿可以从不同的角度出发。
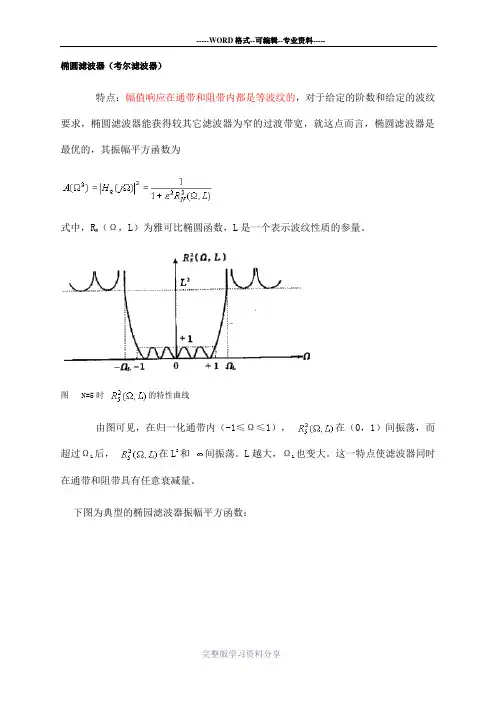
椭圆滤波器(考尔滤波器)
特点:幅值响应在通带和阻带内都是等波纹的,对于给定的阶数和给定的波纹要求,椭圆滤波器能获得较其它滤波器为窄的过渡带宽,就这点而言,椭圆滤波器是最优的,其振幅平方函数为
式中,R
N
(Ω,L)为雅可比椭圆函数,L是一个表示波纹性质的参量。
图 N=5时的特性曲线
由图可见,在归一化通带内(-1≤Ω≤1),在(0,1)间振荡,而
超过Ω
L 后,在L2和间振荡。
L越大,Ω
L
也变大。
这一特点使滤波器同时
在通带和阻带具有任意衰减量。
下图为典型的椭园滤波器振幅平方函数:
图椭圆滤波器的振幅平方函数
图中ε和A的定义与切比雪夫滤波器相同。
、ε和A确定后,阶次N的确定方法为:
当Ωc、Ω
s
式中K(k)=为第一类完全椭圆积分。
上面讨论了三种最常用模拟低通滤波器的特性和设计方法,设计时按照指标要求,合理选用。
一般,椭圆滤波器的阶次可最低,切比雪夫次之,巴特沃兹最高,参数的灵敏度则恰恰相反。
用MATLAB 设计滤波器1 IIR 滤波器的设计freqz功能:数字滤波器的频率响应。
格式:[h ,w ]=freqz (b ,a,n )[h ,f]=freqz(b ,a ,n ,Fs)[h ,w ]=freqz(b ,a,n ,’whole')[h ,f ]=freqz(b,a ,n ,'whole ’,Fs )h=freqz (b ,a ,w)h=freqz (b,a ,f ,Fs)freqz(b ,a)说明:freqz 用于计算由矢量"和b 构成的数字滤波器H (z)=A(z)B(z)= n-1--n -1 l)z a(n ....a(2)z l l)z b(n .... b(2)z b(l)++++++++ 的复频响应H (j ω).[h ,w]=freqz (b,a ,n )可得到数字滤波器的n 点的幅频响应,这n 个点均匀地分布在上半单位圆(即0~π),并将这n 点频率记录在w 中,相应的频率响应记录在h 中。
至于n值的选择没有太多的限制,只要n 〉0的整数,但最好能选取2的幂次方,这样就可采用FFT 算法进行快速计算。
如果缺省,则n=512。
[h ,f ]二freqz(b,a,n ,Fs)允许指定采样终止频率Fs (以Hz 为单位),也即在0~Fs/2频率范围内选取n 个频率点(记录在f 中),并计算相应的频率响应h 。
[h,w]=freqz(b,a,n,’whole’)表示在0~2π之间均匀选取n个点计算频率响应.[h,f]=freqz(b,a,n,'whole',Fs)则在O~Fs之间均匀选取n个点计算频率响应.h=freqz(b,a,w)计算在矢量w中指定的频率处的频率响应,但必须注意,指定的频率必须介于0和2π之间.h=freqz(b,a,f,Fs)计算在矢量f中指定的频率处的频率响应,但指定频率必须介于0和Fs之间。
butter功能:Butterworth(比特沃思)模拟和数字滤波器设计。
和谐校园背景下大学生安全教育策略探究随着我国社会的不断发展,大学校园已成为学子们学习、生活、交流的重要场所。
然而随之而来的问题也不容忽视,大学生安全教育是校园文化建设中的重要部分。
和谐校园建设要求校园安全文化的教育有效实施,为此,本文将从以下几个方面探讨大学生安全教育策略的优化。
一、学校应建立健全安全教育体系对于大学生的安全教育来说,学校是第一责任人,因此建立完善的安全教育体系具有重要意义。
针对不同的学生群体,学校应有针对性地开展安全教育工作,力求做到全员覆盖。
此外,学校还应定期进行模拟演练,以加强学生应急响应的能力。
针对校园安全不到位的问题,学校应加强安保力量投入,严格落实安全措施,切实保障师生的人身安全。
二、师生应增强安全意识安全教育不是一次性活动,师生在日常生活中应增强安全意识,做到警钟长鸣。
例如,在日常学习生活中,要注意电器使用安全、防火、防盗、防感染等;校外出行应注意个人安全防范,如尽量避免夜晚独自外出、不要在人多混乱的场合待太久等。
此外,师生应当积极参加校园安全教育活动,加强安全知识的学习,提升防范意识和自我保护能力。
三、加强学生心理教育大学生心理素质较差,心理问题也多样化、复杂化。
良好的心理状态对于大学生的安全保障至关重要。
学校要建立心理咨询体系,为学生提供心理健康方面的支持,如心理咨询、心理疏导、心理干预、心理辅导等。
另外,通过心理辅导的途径加强大学生自我保护能力,提升心理承受能力。
四、加强家长的安全保障意识学生的安全教育,不仅仅在学校中进行,家庭也是重要场所之一。
因此,除了学校和学生自己的努力外,家长的支持和配合同样重要。
家长应加强对学生的关心和照顾,了解学生所面临的问题,做到及时干预和帮助。
同时,家长也应加强自身的安全保障意识,掌握一定的安全知识,将自己的安全观念传达给孩子。
综上所述,大学生安全教育是校园建设的重要组成部分,而和谐校园的实现,离不开学校、师生、家长的共同努力。
第一章摘要本文简单、直观地介绍了椭圆低通滤波器的基本理论和设计思想,阐述了设计椭圆低通滤波器的具体步骤,利用MATLAB产生一个包含低频、中频、高频分量的连续信号,并实现对连续信号进行的采样。
文中还对采样信号进行频谱分析,利用设计的椭圆滤波器对采样信号进行滤波处理,并对仿真结果进行分析和处理。
详细介绍了在用MATLAB设计椭圆滤波器用到的工具和命令。
第二章引言信号处理是科学研究和工程技术许多领域都需要进行的一个重要环节,传统上对信号的处理大都采用模拟系统实现。
随着人们对信号处理要求的日益提高,以及模拟信号处理中一些不可克服的缺点,对信号的许多处理而采用数字的方法进行。
近年来由于大规模集成电路和计算机技术的进步,信号的数字处理技术得到了飞速发展。
数字信号处理系统无论在性能、可靠性、体积、耗电量、成本等诸多方面都比模拟信号处理系统优越的多,使得许多以往采用模拟信号处理的系统越来越多地被数字处理系统所代替,数字信号处理技术在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
在数字信号处理中,数字滤波器十分重要并已获得广泛应用,数字滤波器与模拟滤波器比较,具有精度高、稳定、体积小、重量轻、灵活、不要求阻抗匹配以及实现模拟滤波器无法实现的特殊滤波功能等优点。
在各种滤波器中,椭圆滤波器具有其独特的优点。
本次设计中所用到数学软件为MATLAB。
MATLAB和Mathematica、Maple并称为三大数学软件,它是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortran)的编辑模式,代表了当今国际科学计算软件的先进水平。
椭圆带通滤波器的设计燕山大学课程设计说明:椭圆带通滤波器设计学院(系)名称:电气工程学院年级专业:12年级学校编号:学生姓名:讲师:教师职称:电气工程学院《课程设计》作业课程名称:数字信号处理课程设计基础教学单元;仪器科学与工程系讲师;学生姓名(专业)课程设计主题2椭圆带通滤波器技术参数的设计采样频率100赫兹,采样数100,低频、中频和高频信号频率分别为5Hz、15Hz和30Hz。
设计要求对连续信号进行采样和频谱分析,包括低频、中频和高频分量。
设计一个高通滤波器对信号进行滤波,观察滤波后信号的频谱。
(熟悉函数freqz,ellip,filter,fft)参考数据数字信号处理数据MATLAB 数据内容采集消化数据,学习MATLAB软件,计算相关参数,编写仿真程序,签署调试指导,签署基层教学单位主任在上半年的指令:1.本表一式四份,系、讲师、学生各一份,学院教务处一份。
2.学生的作业书需要装订在课程设计报告的前面。
电气工程学院教务处概要中的所谓数字滤波器,是指输入和输出都是数字信号,并且输入信号中包含的频率分量的相对比例通过数值计算处理而改变,或者某些频率分量被滤除的数字设备或程序。
该数字滤波器具有处理精度高、稳定、体积小、重量轻、灵活、无阻抗匹配问题的优点。
典型的模拟滤波器包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器和贝塞尔滤波器,其中椭圆滤波器具有更好的性能。
Matlab是一套集数值计算、符号计算和图形处理等强大功能于一体的科学计算软件。
作为一个强大的科学计算平台,它可以满足几乎所有的计算需求。
本课结合MATLAB设计一个模拟椭圆滤波器。
文字数据目录第1章简介第1章信号处理原理第2章椭圆滤波器基本理论第22.2章采样定理第3章软件仿真设计第43.1章椭圆滤波器设计结构图第43.2章设计椭圆模拟带通滤波器的步骤第43.3章MATLAB相关函数简介第4章程序和仿真结果分析第84.1章带通滤波器设计程序第84.2章仿真结果KK和分析第9章参考文献第13章文字数据简介椭圆滤波器又称考尔滤波器。
燕山大学课程设计说明书题目:椭圆带通滤波器的设计学院(系):电气工程学院年级专业: 12级学号:学生姓名:指导教师:教师职称:电气工程学院《课程设计》任务书课程名称:数字信号处理课程设计基层教学单位:仪器科学与工程系指导教师:说明:1、此表一式四份,系、指导教师、学生各一份,报送院教务科一份。
2、学生那份任务书要求装订到课程设计报告前面。
电气工程学院教务科摘要所谓数字滤波器,是指输入输出均为数字信号,通过数值运算处理改变输入信号所含频率成分的相对比例,或者滤除某些频率成分的数字器件或程序。
数字滤波器处理精度高、稳定、体积小、重量轻、灵活、不存在阻抗匹配问题。
典型的模拟滤波器有巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器和贝塞尔滤波器,其中椭圆滤波器具有较好的性能。
Matlab是一套集数值计算、符号运算及图形处理等强大功能于一体的科学计算软件。
作为强大的科学计算平台,它几乎能够满足所有的计算需求。
本课结合MATLAB设计模拟椭圆滤波器。
目录第一章概论---------------------------------------------------------------------------------- 2 第二章信号处理原理 --------------------------------------------------------------------- 32.1椭圆滤波器的基本理论 ---------------------------------------------------------- 32.2采样定理 ---------------------------------------------------------------------------- 3 第三章软件仿真设计 --------------------------------------------------------------------- 53.1椭圆滤波器设计结构图 ---------------------------------------------------------- 53.2设计椭圆模拟带通滤波器的步骤 ---------------------------------------------- 53.3 MATLAB相关函数介绍--------------------------------------------------------- 5 第四章程序和仿真结果分析 ------------------------------------------------------------ 84.1带通通滤波器设计程序 ---------------------------------------------------------- 84.2仿真结果KK及分析 ------------------------------------------------------------- 9 参考文献 ------------------------------------------------------------------------------------- 12第一章概论椭圆滤波器又称考尔滤波器。
椭圆函数滤波器
维基百科,自由的百科全书
椭圆滤波器(Elliptic filter)又称考尔滤波器(Cauer filter),是在通带和阻带等波纹的一种滤波器。
椭圆滤波器相比其他类型的滤波器,在阶数相同的条件下有着最小的通带和阻带波动。
它在通带和阻带的波动相同,这一点区别于在通带和阻带都平坦的巴特沃斯滤波器,以及通带平坦、阻带等波纹或是阻带平坦、通带等波纹的切比雪夫滤波器。
一个低通椭圆滤波器的频率响应的幅度为:
四阶低通椭圆滤波器的频率响应。
其中R n是n阶雅可比椭圆函数(Chebyshev rational functions)。
[编辑]与其他线性滤波器的比较
下图给出了椭圆滤波器与其他常见滤波器的比较,各滤波器的参数一样多。
1 / 1
由图可见,椭圆滤波器比其他滤波器更陡,因此在选择滤波器的时候,椭圆滤波器能够以较低的阶数获得较窄的过渡带宽,但是它在通带和阻带上都有波动。
(注:本资料素材和资料部分来自网络,仅供参考。
请预览后才下载,期待您的好评与关注!)。