随机事件的关系与运算
- 格式:ppt
- 大小:1016.82 KB
- 文档页数:32

概率论与数理统计主讲:四川大学四川大学第2讲随机事件的关系与运算1第2讲随机事件的关系与运算四川大学四川大学第2讲随机事件的关系与运算3在上一讲第1 讲随机试验样本空间随机事件我们介绍了样本空间、样本点和事件的概念这一讲我们来讲事件的运算四川大学第2讲随机事件的关系与运算4§1.2样本空间随机事件四川大学第2讲随机事件的关系与运算5(三)随机事件的关系与运算四川大学第2讲随机事件的关系与运算6回忆事件的概念随机试验E 的样本空间S的子集A 称为E 的随机事件,简称事件。
当A 中某一个样本点出现时,就说事件A 发生了。
由一个样本点e 组成的单点集{e} 称为基本事件。
一般的事件是由基本事件复合而成的,而基本事件是不能再分解的事件。
四川大学第2讲随机事件的关系与运算7一个事件A 是样本空间S的一个子集,因此事件之间的关系以及事件的运算可以用集合之间的关系和集合运算来处理。
设试验E的样本空间为S,而A, B,(k=1, 2,…)是S的子集。
Ak四川大学第2讲随机事件的关系与运算8事件间的关系四川大学第2讲随机事件的关系与运算10第2讲随机事件的关系与运算12四川大学2. 事件的相等如果事件A 包含事件B ( ),事件B 也包含事件A ( ) ,即A 与B 有相同的样本点,则称事件A 与事件B 相等,记作A B=即A B =⇔and A B B A⊂⊂A B ⊃A B ⊂第2讲随机事件的关系与运算13四川大学例如,记A =“考试及格”,B =“考试成绩为90分”记C =“至少有50人排队”,D =“至少有30人排队”抛两颗骰子,两颗骰子出现的点数分别记为x 和y .记E =“x +y 为奇数”,F =“两次的骰子点数奇偶性不同”{|60100}A x x =≤≤C D ⇒⊂E F⇒=A B ⇒⊃{90}B ={50,51,...}C ={30,31,...}D =事件的运算四川大学第2讲随机事件的关系与运算14第2讲随机事件的关系与运算16四川大学1kk A ∞=∑1k k A ∞= 12...n A A A n 个事件A 1, A 2, …, A n 中至少有一个发生的事件称为这些事件的和事件,1nkk A == 12...n A A A +++1nkk A ==∑或可列个事件A 1, A 2, …A n , …中至少有一个发生的事件称为这些事件的和事件,或事件的并(和)可以推广到有限或可列个事件。






随机事件的关系与运算随机事件是指在一定条件下具有随机性质的事件,其发生与否是由随机因素决定的。
在随机事件中,我们需要对其进行运算,以便得到更加准确的结果。
本文将从随机事件的关系与运算角度,对随机事件的基本概念、性质、运算规则等进行探讨。
一、随机事件的基本概念与性质随机事件是指在一定条件下具有随机性质的事件,其发生与否是由随机因素决定的。
随机事件的基本概念包括:样本空间、随机事件、必然事件和不可能事件。
样本空间是指一个试验中所有可能的结果构成的集合,记作S。
随机事件是指样本空间S中的一个子集,即一个具有一定概率的事件。
必然事件是指在样本空间中所有结果都属于该事件的事件,记作Ω。
不可能事件是指在样本空间中没有任何结果属于该事件的事件,记作∅。
随机事件具有以下性质:1. 互斥性:若两个事件A和B之间没有公共结果,则称它们互斥。
2. 相对补集:若事件A的发生导致事件B的不发生,则称事件A是事件B的补事件,记作A的补集,即A^c。
3. 包含关系:若事件A的发生导致事件B的发生,则称事件A包含事件B,记作A⊇B。
二、随机事件的运算规则在随机事件的运算中,我们需要对事件之间的关系进行分析和计算。
随机事件的运算包括并、交、差和补四种运算。
1. 并运算并运算是指将两个事件A、B的结果集合并为一个结果集的操作,用符号“∪”表示。
即:A∪B={x|x∈A或x∈B}。
并运算的性质:(1)交换律:A∪B=B∪A。
(2)结合律:(A∪B)∪C=A∪(B∪C)。
(3)分配律:A∩(B∪C)=(A∩B)∪(A∩C)。
2. 交运算交运算是指将两个事件A、B的公共结果构成一个新的事件的操作,用符号“∩”表示。
即:A∩B={x|x∈A且x∈B}。
交运算的性质:(1)交换律:A∩B=B∩A。
(2)结合律:(A∩B)∩C=A∩(B∩C)。
(3)分配律:A∪(B∩C)=(A∪B)∩(A∪C)。
3. 差运算差运算是指事件A中除去事件B的结果所构成的新事件,用符号“-”表示。



有关随机事件关系和运算的例析随机事件是概率论中的基础概念,是指在某一实验中可能发生的事件。
在实际应用中,我们常常需要对多个随机事件进行关系和运算,以求得更为准确的结果。
下面,我们将通过一些例子,来深入探究随机事件的关系和运算。
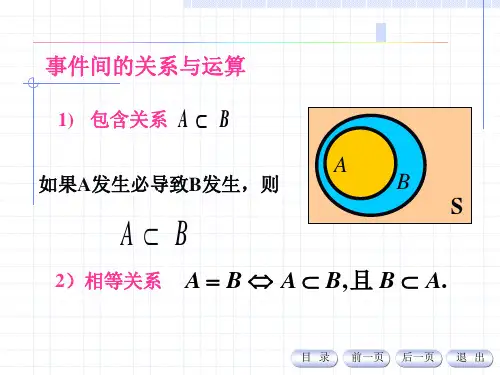
一、事件的关系1. 包含关系当事件A包含事件B时,我们可以表示为 AB。
例如:在掷一枚骰子的实验中,事件A表示掷出的点数是偶数,事件B表示掷出的点数是2。
显然,事件B包含在事件A中,即 AB。
2. 相等关系当事件A和事件B所包含的样本点完全相同时,我们可以表示为A=B。
例如:在掷一枚骰子的实验中,事件A表示掷出的点数是偶数,事件B表示掷出的点数不是偶数。
显然,事件A和事件B所包含的样本点完全相同,即 A=B。
3. 互斥关系当事件A和事件B所包含的样本点没有交集时,我们可以表示为A∩B=。
例如:在掷一枚骰子的实验中,事件A表示掷出的点数是偶数,事件B表示掷出的点数是奇数。
显然,事件A和事件B所包含的样本点没有交集,即 A∩B=。
4. 独立关系当事件A和事件B的发生与否互不影响时,我们可以表示为P(A|B)=P(A) 或 P(B|A)=P(B)。
例如:在掷一枚骰子的实验中,事件A表示掷出的点数是偶数,事件B表示掷出的点数大于3。
显然,事件A和事件B的发生与否互不影响,即 P(A|B)=P(A) 或 P(B|A)=P(B)。
二、事件的运算1. 并集运算当事件A和事件B中至少有一个发生时,我们可以表示为 A∪B。
例如:在掷一枚骰子的实验中,事件A表示掷出的点数是偶数,事件B表示掷出的点数是3。
显然,事件A和事件B中至少有一个发生,即 A∪B。
2. 交集运算当事件A和事件B同时发生时,我们可以表示为 A∩B。
例如:在掷一枚骰子的实验中,事件A表示掷出的点数是偶数,事件B表示掷出的点数是4。
显然,事件A和事件B同时发生,即 A∩B。
3. 补集运算当事件A不发生时,我们可以表示为 A'。