编号03青岛九中2010级高二数学学案§1青岛

2022-2023学年山东省青岛市青岛第九中学高二上学期期中数学试题一、单选题1．双曲线的渐近线方程是（ ）2214y x -=A ．B 0x =0y ±=C ．D ．20x y ±=20x y ±=【答案】C【分析】根据双曲线的标准方程，即可直接求出其渐近线方程.【详解】∵双曲线的标准方程为，2214y x -=∴双曲线的焦点在轴，，，且双曲线的渐近线方程为，即.y 2a =1b =2ay x x b =±=±20x y ±=故选：C.2．若两个不同平面的法向量分别为，则（ ）,αβ()()1,2,1,3,6,3u v =-=--A ．B ．C ．相交但不垂直D ．以上均不正确//αβαβ⊥,αβ【答案】A【分析】根据法向量，可得，可得法向量和平行即可得解.()()1,2,1,3,6,3u v =-=--3v u =- v u【详解】由，3v u =-所以法向量和平行，v u所以平面和平行，αβ故选：A.3．已知圆的圆心，一条直径的两个端点恰好在两坐标轴上，则这个圆的方程为C (2,3)-A ．B ．22460x y x y +-+=224680x y x y +-++=C ．D ．22460x y x y +--=224680x y x y +-+-=【答案】A【详解】设直径的两个端点分别A （a ，0）B （0，b ）．圆心C 为点（2，﹣3），由中点坐标公式得，a=4，b=﹣6，∴r=1AB 2==则此圆的方程是（x﹣2）2+（y+3）2=13，即x 2+y 2﹣4x+6y=0．故选A ．4．过点作直线分别与轴、轴的正半轴交于、两点，点为坐标原点，则()4,2P l x y A B O 的最小值为（ ）OA OB+ A ．B ．C ．D．2+6+6【答案】C【解析】由题意可知直线的斜率存在，设直线的方程为，根据已知条件求出的l l ()24y k x -=-k 取值范围，并求出、两点的坐标，再利用基本不等式可求得的最小值.A B OA OB+ 【详解】由于过点作直线分别与轴、轴的正半轴交于、两点，则直线的斜率存在，()4,2P l x y A B l 设直线的方程为，即，l ()24y k x -=-240kx y k -+-=在直线的方程中，令，可得，即点；l 0y =42k x k -=42,0k A k-⎛⎫ ⎪⎝⎭令，可得，即点.0x =24y k =-()0,24B k -由题意可得，解得，420240k k k -⎧>⎪⎨⎪->⎩0k <所以，()422246466k OA OB k k k k -+=+-=+-+≥+=+- 当且仅当k =因此，的最小值为.OA OB+ 6+故选：C.【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.5．如图，在长方体中，，，点在线段上，且，1111ABCD A B C D -12AA AD ==3AB =F 11C D 11D F =则异面直线与所成角的余弦值为（ ）CDBF ABC ．D23【答案】B【分析】构建空间直角坐标系，求，的坐标，应用空间向量夹角的坐标表示求与所DC BF CD BF 成角的余弦值即可.【详解】如图，以为坐标原点，建立空间直角坐标系，则，，D D xyz -()0,0,0D ()0,3,0C ，，()2,3,0B ()0,1,2F ∴，.()0,3,0DC =()2,2,2BF =--∴，cos ,DC BF DC BF DC BF ⋅〈〉===∴异面直线与CD BF 故选：B6．已知圆截直线所得的弦的长度为，则等于22()4x a y -+=4y x =-a A ．2B ．6C ．2或6D．【答案】C【详解】∵圆截直线 所得的弦的长度为，圆心到直线()224x a y -+=4y x =-(),0a 的距离∴，解得 或 ．故选C ．4y x =-d =2a =6a =7．椭圆上的点到直线的最大距离是（ ）221164x y +=20x y +=A．3B C ．D 【答案】D【分析】设椭圆上的点P （4cosθ，2sinθ），由点到直线的距离公式，计算221164x y +=20x y +=可得答案．【详解】设椭圆上的点P （4cosθ，2sinθ）221164x y +=则点P 到直线的距离20x y +=D ．max d 【点睛】本题考查直线和椭圆的位置关系，解题时要认真审题，仔细求解．8．已知圆和两点，，若圆上存在点，使得()()22:341C x y -+-=(),0A m -()(),00B m m >C P ，则的最大值为90APB ∠=︒m A ．7B ．6C ．5D ．4【答案】B【详解】由题意知，点P 在以原点（0，0）为圆心，以m 为半径的圆上，又因为点P 在已知圆上，所以只要两圆有交点即可，所以，故选B.15m -=【解析】本小题主要考查两圆的位置关系，考查数形结合思想，考查分析问题与解决问题的能力.二、多选题9．如图，一个结晶体的形状为平行六面体，其中，以顶点A 为端点的三条棱长均1111ABCD A B C D -为6，且它们彼此的夹角都是，下列说法中不正确的是（ ）60︒A ．16AC =B ．1AC BD⊥C ．向量与的夹角是1B C 1AA60︒D ．与AC 1BD 【答案】ACD【分析】根据题意，利用空间向量的线性运算和数量积运算，对选项中的命题分析，判断正误即可．【详解】解：对于A ，111:AC AB BC CC AB AD AA =++=++ ∴22221111222AC AB AD AA AB AD AD AA AD AA =+++⋅+⋅+⋅ ，363636266cos60266cos60266cos60216=+++⨯⨯⨯︒+⨯⨯⨯︒+⨯⨯⨯︒=所以A 错误；1||AC 对于B ：221111()()2AC BD AB AD AA AD AB AB AD AB AD AA AD AA AB ⋅=++⋅+=⋅+++⋅+⋅，66cos603666cos603666cos6066cos600=⨯⨯︒++⨯⨯︒--⨯⨯︒-⨯⨯︒=所以，即，选项B 正确；10AC DB ⋅=1AC DB ⊥对于C ：向量 与 的夹角是，所以向量 与的夹角也是，选项1B C 1BB 18060120︒-︒=︒1B C 1AA 120︒C 错误；对于D ：，11BD AD AA AB =+- AC AB AD=+得，()2211||BD AD AA AB=+-1||BD ∴=同理，可得||AC = ，11(AC BD AD AA AB ⋅=+- )()18183636181836AB AD ⋅+=+-++-=所以D 错误．111cos ||AC BD BD AC AC BD ⋅<⋅>==⋅故选：ACD ．10．已知椭圆的左､右焦点分别为，为椭圆上不同于左右顶点的任意一点，22:143x y C +=12F F 、P C 则下列说法正确的是（）A ．的周长为B ．12PF F △812PF F △C ．的取值范围为D ．的取值范围为12PF PF ⋅[23)，12||||PF PF (34]，【答案】BCD【分析】计算周长得到6，A 错误，B 正确，，根据定义域得到范S 212124PF PF x ⋅=+ 围，C 正确，，得到值域，得到答案.()21224PF PF t ⋅=--+【详解】根据题意：，，，2a =b =1c =的周长为，A 错误；12PF F △22426a c +=+=面积的为在上下顶点时等号成立，B 正确；12PF F △S P 设，则，(),P x y ()()2222212311,1,113244PF PF x y x y x y x x x ⋅=---=-+=-+-=+ ，故，C 正确；()2,2x ∈-[)122,3PF PF ⋅∈，设，，1224PF PF a +==1PF t=()1,3t ∈则，故的取值范围为，D 正确.()()22124424PF PF t t t t t ⋅=-=-+=--+12PF PF ⋅(34]，故选：BCD.11．如图，四边形是边长为的正方形，平面，平面，且ABCD 1ED ⊥ABCD FB ⊥ABCD ，为线段上的动点，则下列结论中正确的是（ ）1ED FB ==G ECA ．B ．该几何体外接球的体积为EC AF⊥3πC ．若为中点，则平面D ．的最小值为G EC //GB AEF 22AG BG +114【答案】ACD【分析】以为原点，、、所在直线分别为轴、轴、轴，建立空间直角坐标系，D DA DC DE x y z 分别求得，，，，，的坐标，由，的数量积可判断A 选项；该几何体外接球D A B CF E AF EC的球心为矩形的对角线交点，即可求得半径，可判断B 选项；求得的坐标，求得平面BDEF G 的法向量，计算可判断C 选项；设（），由两点的距离公式，结合二次函AEF ()0,,1G t t -01t ≤≤数的最值求法，可判断D 选项．【详解】由题意以为原点，、、所在直线分别为轴、轴、轴，建立如图所示空D DA DC DE x y z 间直角坐标系，可得，，，，，，(0,0,0)D (1,0,0)A (1,1,0)B (0,1,0)C (1,1,1)F (0,0,1)E 对于A 选项：有，，由，可得即，(0,1,1)EC =- (0,1,1)AF = 0110AF EC ⋅=+-= EC AF ⊥EC AF ⊥所以A 选项正确；对于B 选项：由球的截面性质可知，球心在过正方形的中心的垂面上，即为矩形的对ABCD BDEF 角线的交点，则该球的半径1122R ===即该几何体外接球的体积B 选项错误；334π4π33V R ==⨯=对于C 选项：若为中点，则，G EC 110,,22G ⎛⎫⎪⎝⎭即，，，111,,22BG ⎛⎫=-- ⎪⎝⎭ (1,0,1)AE =-(0,1,1)AF = 设平面的法向量为，AEF (,,)n x y z = 由，令，可得，00n AE x z n AF y z ⎧⋅=-+=⎪⎨⋅=+=⎪⎩ 1x =(1,1,1)n =- 即，可得，111022BG n ⋅=-++= BG n ⊥ 又平面，则平面，所以C 选项正确；BG ⊄AEF GB //AEF 对于D 选项：由三角形是等腰直角三角形，可设（），EDC (0,,1)G t t -01t ≤≤则，222222311465444AG BG t t t ⎛⎫+=+=-+=-+⎪⎝⎭又，则当时，取得最小值，所以D 选项正确．01t ≤≤3t 4=22AG BG +114故选：ACD.12．卵形曲线也叫卵形线，是常见曲线的一种，分笛卡尔卵形线和卡西尼卵形线.卡西尼卵形线是平面内与两个定点（叫做焦点）距离之积等于常数的点的轨迹.设焦点是平面内12(0)(0)F c F c -，，，两个定点，（是定长），特别地，当时的卡西尼卵形线又称为伯努利双纽线，212||||PF PF a ⋅=a c a =某同学通过类比椭圆与双曲线的研究方法，对伯努利双纽线进行了相关性质的探究，得到下列结论，其中正确的是（ ）A ．曲线过原点B ．关于原点中心对称且关于坐标轴成轴对称C ．方程为222222()2()x y a x y +=-D ．曲线上任意点，，00()P x y ，0[]x a a ∈-，0[]22a a y ∈-，【答案】ABC【分析】根据得到轨迹方程为得到ABC 正确，验证知212||||PF PF a ⋅=222222()2()x y a x y +=-在曲线上，故D 错误，得到答案.),0【详解】设，时，，(),P x y c a =212||||PF PF a ⋅==化简得到：，故C 正确；222222()2()x y a x y +=-曲线过原点，A 正确；关于原点中心对称且关于坐标轴成轴对称，B 正确；验证知在曲线上，故D 错误.),0故选：ABC.三、填空题13．直线与直线平行，则的值为____________．1:330l mx y m +++=2:220l x y -+=m 【答案】##32-1.5-【分析】利用直线的一般式方程确定两直线平行的条件即可求解.【详解】因为直线与直线平行，1:330l mx y m +++=2:220l x y -+=所以，解得,()()()×21×3=03×22+30m m ----≠⎧⎪⎨⎪⎩32m =-所以的值为.m 32-故答案为：.32-14．记双曲线的离心率为e ，写出满足条件“直线与C 无公共点”的e2222:1(0,0)xy C a b a b -=>>2y x =的一个值______________．【答案】2（满足1e <≤【分析】根据题干信息，只需双曲线渐近线中即可求得满足要求的e 值.by x a =±02b a <≤【详解】解：，所以C 的渐近线方程为,2222:1(0,0)x y C a b a b -=>>b y x a =±结合渐近线的特点，只需，即，02b a <≤224b a≤可满足条件“直线与C 无公共点”2y x =所以===c e a又因为，所以，1e >1e <≤故答案为：2（满足1e <≤15．如图，已知圆是圆上两个动点，点，则矩形的顶点的轨22:16,,O x y A B +=O (2,0)P PACB C 迹方程是___________．【答案】2228x y +=【解析】设点，连接交于，可写出的坐标，再在直角中，(,)C x y ,AB PC M M OMB △，利用勾股定理列方程可得x, y 的关系式，即顶点的轨迹方程.OM MB ⊥C 【详解】设点，如图连接交于，(,)C x y ,AB PC M 由矩形可知为的中点，，PACB M PC 2,22x y M +⎛⎫ ⎪⎝⎭PM MB =连接，在直角中，，则,OB OM OMB △OM MB ⊥22222OB OM BM OM MP=+=+即，整理得，2222221622222x y x y +++⎛⎫⎛⎫⎛⎫⎛⎫=+-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2228x y +=所以顶点的轨迹方程是C 2228x y +=故答案为：2228x y +=【点睛】关键点睛：本题考查求轨迹方程，解题的关键是求谁设谁，设点，然后再利用图(,)C x y 像的几何关系找到x, y 的关系式，即求得轨迹方程，考查学生的直观想象能力与运算求解能力，属于中档题.四、双空题16．已知点是空间直角坐标系 内一点， 则点 关于 轴的对称点 的()1,2,3P O xyz -P x Q 坐标为 ________． 若点 在平面 上的射影为 ， 则四面体 的体积为P xOy M O PQM -________．【答案】 （1，－2，－3） 2【分析】由空间直角坐标系中的点的对称性质求解，利用棱锥的体积公式直接求解【详解】是空间直角坐标系 内一点， 则点 关于 轴的对称点 的 坐()1,2,3P O xyz -P x Q 标为（1，－2，－3），因为点 在平面 上的射影为 ，所以，P xOy M (1,2,0)M 所以四面体 的体积为，O PQM -112213232⨯⨯⨯⨯⨯=故答案为：（1，－2，－3），2五、解答题17．已知斜率为的直线与圆心为的圆相切于点，且点在轴上.1l 1(1,0)O P P y （1）求圆的方程；1O（2）若直线与直线平行，且圆上恰有四个不同点到直线，求直线纵截距的l 'l 1O l 'l '取值范围.【答案】（1）；（2）.22(1)2x y -+=()2,0-【解析】（1）由题意可知，从而可得，求出，再由.1O P l ⊥0101t -=--1t =1||r O P ==（2）设：，由题意可得圆心到直线的距离.l 'y x b =+y x b =+d 【详解】解：（1）依题意，设点的坐标为.，，解得，P (0,)t 1O P l ⊥∴0101t -=--1t =即点的坐标为，从而圆的半径.P (0,1)1O 1||r O P ==故所求圆的方程为.1O 22(1)2x y -+=（2）因为，设：，//l l 'l 'y x b =+由圆上恰有四个不同点到直线，1O l '得圆心到直线的距离，y x b =+d 解得.即直线纵截距的取值范围为.20b -<<l '()2,0-18．已知椭圆．2222x y C 1a b +=：()0,0a b >>4（1）求椭圆的标准方程；（2）已知过点P （2,1）作弦且弦被P 平分，则此弦所在的直线方程.【答案】(1) (2) 221164x y +=240x y +-=【详解】试题分析：（1）根据椭圆的性质列方程组解出a，b ，c 即可；（2）设直线斜率为k ，把直线方程代入椭圆方程，根据根与系数的关系和中点坐标公式列方程即可得出k的值，从而求出直线方程．试题解析：（1）2b=4，所以a=4，b=2，c=c e a ==221164x y +=（2）设以点为中点的弦与椭圆交于，则，分别代入()2,1P ()()1122,,,A x y B x y 12124,2x x y y +=+=椭圆的方程，两式相减得，所以，()()()()1212121240x x x x y y y y +-++-=()()1212480x x y y -+-=所以，由直线的点斜式方程可知，所求直线方程为，即121212y y k x x -==--()1122y x -=--．240x y +-=点睛：弦中点问题解法一般为设而不求，关键是求出弦AB 所在直线方程的斜率k,方法一利用点差法，列出有关弦AB 的中点及弦斜率之间关系求解；方法二是直接设出斜率k ，利用根与系数的关系及中点坐标公式求得直线方程.19．已知的顶点，直线的方程为，边上的高 所在直线的方ABC ()2,8C -AB 211y x =-+AC BH 程为.320x y ++=(1)求顶点和的坐标；A B (2)求外接圆的一般方程.ABC 【答案】(1)，()5,1A ()7,3B -(2)2246120x y x y +-+-=【分析】（1）联立直线，的方程求出点的坐标，由求出直线的斜率及方程，BH AB B AC BH ⊥AC 的方程与直线方程联立求出的坐标；AC AB A （2）设圆的一般方程为，将，，三点坐标代入求出圆的一般方程求出220x y Dx Ey F ++++=A B C 的值即可求解.,,D E F 【详解】（1）由可得，所以点的坐标为，211320y x x y =-+⎧⎨++=⎩73x y =⎧⎨=-⎩B ()7,3-由可得，所以320x y ++=1233y x =--13BH k =-由，可得，AC BH ⊥3AC k =因为，所以直线 的方程为：，即，()2,8C -AC ()832y x +=-3140x y --=由可得，所以点的坐标为.2113140y x x y =-+⎧⎨--=⎩51x y =⎧⎨=⎩A ()5,1（2）设的外接圆方程为，ABC 220x y Dx Ey F ++++=将，和三点的坐标分别代入圆的方程可得：()5,1A ()7,3B -()2,8C -，解得：，52607358028680D E F D E F D E F +++=⎧⎪-++=⎨⎪-++=⎩4612D E F =-⎧⎪=⎨⎪=-⎩所以的外接圆的一般方程为.ABC 2246120x y x y +-+-=20．在正四棱柱中在线段上.1111ABCD A B C D -1,2,4,AB AA E ==1CC（1）若平面，求的长；1A C ⊥BDE CE （2）在（1）的条件下，求直线与平面所成角的正弦值.1D E BDE【答案】（1）；（2.1【分析】（1）由已知可得两两垂直，建立空间直角坐标系，利用已知条件写出1,,DA DC DD D xyz -点的坐标，设()，进而得到点的坐标，利用平面，CE a =04a <<E 1A C ⊥DBE 可得，即可得出的值，即可得出结果；（2）由（1）得，1440A C DE a ⋅=-=a ()10,2,3D E =- 为平面的一个法向量，利用线面的所成角的向量求法求解即可.1AC DBE 【详解】解：（1）由已知可得两两垂直，1,,DA DC DD 建立如图所示的空间直角坐标系，D xyz -可得，()()()()0,0,0,2,0,0,2,2,0,0,2,0D A B C ，()()()()11110,0,4,2,0,4,2,2,4,0,2,4D A B C 设()，CE a =04a <<则，()0,2,E a ，()()()10,2,,2,2,0,2,2,4DE a DB A C ===--∴，1440A C DB ⋅=-+=∴.1AC DB ⊥由平面，1A C ⊥DBE得，1440A C DE a ⋅=-=解得，1a =即的长为.CE 1（2）由（1）得，()10,2,3D E =-为平面的一个法向量，1AC DBE ∴11cos ,D E A C ==∴与平面.1D EDBE 21．如图，直三棱柱的体积为4，的面积为111ABC A B C -1A BC (1)求A 到平面的距离；1A BC (2)设D 为的中点，，平面平面，求二面角的正弦值．1A C 1AA AB =1ABC ⊥11ABB A ABD C --【答案】【分析】（1）由等体积法运算即可得解；（2）由面面垂直的性质及判定可得平面，建立空间直角坐标系，利用空间向量法即BC ⊥11ABB A 可得解.【详解】（1）在直三棱柱中，设点A 到平面的距离为h ，111ABC A B C -1A BC则，111111111143333A A BC A A ABC A ABC A B BC C C B V S h V S A A V ---=⋅===⋅==解得h =所以点A 到平面1A BC （2）取的中点E ,连接AE ,如图，因为，所以,1A B 1AA AB =1AE A B ⊥又平面平面，平面平面，1A BC ⊥11ABB A 1A BC ⋂111ABB A A B =且平面，所以平面，AE ⊂11ABB A ⊥AE 1A BC 在直三棱柱中，平面，111ABC A B C -1BB ⊥ABC 由平面，平面可得，，BC ⊂1A BC BC ⊂ABC AE BC ⊥1BB BC ⊥又平面且相交，所以平面，1,AE BB ⊂11ABB A BC ⊥11ABB A 所以两两垂直，以B 为原点，建立空间直角坐标系，如图，1,,BC BA BB 由（1）得，，AE =12AA AB ==1A B =2BC =则,所以的中点，()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C 1A C ()1,1,1D 则，,()1,1,1BD =()()0,2,0,2,0,0BA BC ==设平面的一个法向量，则，ABD (),,m x y z = 020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩可取，()1,0,1m =-设平面的一个法向量，则，BDC (),,n a b c = 020n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩可取，()0,1,1n =-则，1cos ,2m n =所以二面角A BD C --=22．已知椭圆的左､右焦点分别为，过的直线与椭圆交于两2222:1(0)x y C a b a b +=>>12,F F 2F l C ,AB 点，点为椭圆的下顶点，轴时，的面积为.PC 2PF =l x ⊥AOB （1）求椭圆的标准方程；C （2）当直线不过坐标原点时，求的取值范围.l 11F A F B ⋅【答案】（1）；（2）.22184x y +=(]4,14-【分析】（1）由已知建立关于的方程组，解之可求得椭圆的标准方程.,,a b c C （2）由（1）知，设，，由直线不过坐标原点，所以设直线的方程为1(2,0)F -11(,)A x y 22(,)B x y l l ，与椭圆的方程联立得，得出根与系数的关系式，表示，2x my =+()222440m y my ++-=11F A F B ⋅ 代入可求得的取值范围.11F A F B ⋅【详解】（1）因为为直角三角形，所以，则，2 POF 22222)b c PF+==b c =又，22122AOBb b cS c a a =⨯⨯== 2b c=又，所以，则，222a b c =+34b b ==24b =，故椭圆的标准方程为222448a b c =+=+=C 22184x y +=（2）由（1）知，设，，1(2,0)F -11(,)A x y 22(,)B x y 则，，()1112,F A x y =+()1222,F B x y =+又直线不过坐标原点，所以设直线的方程为，则，l l 2x my =+222184x my x y =+⎧⎪⎨+=⎪⎩消去得，x ()222440m y my ++-=所以，，12242my y m -+=+12242y y m -=+则111212(2)(2)F A F B x x y y ⋅=+++1212(4)(4)my my y y =+++，21212(1)4()16m y y m y y =++++()22244141622mm m m m --=++⋅+++23642m =-++因为，所以，所以，222m +≥2360182m <≤+23644142m -<-+≤+所以，即的取值范围是.11F A F B ⋅ (]4,14∈-11F A F B⋅(]4,14-【点睛】方法点睛：(1)解答直线与椭圆的题目时，时常把两个曲线的方程联立，消去 (或)建立x y 一元二次方程，然后借助根与系数的关系，并结合题设条件建立有关参变量的等量关系；(2)涉及到直线方程的设法时，务必考虑全面，不要忽略直线斜率为或不存在等特殊情形．有时若直线过x 0轴上的一点，可将直线设成横截式.。

一、多选题1．正方形ABCD 的边长为1，记AB a =，BC b =，AC c =，则下列结论正确的是（ ）A ．()0a b c -⋅=B ．()0a b c a +-⋅= C ．()0a c b a --⋅=D ．2a b c ++=2．在ABC 中，a ，b ，c 分别是内角A ，B ，C 2sin c A =，且02C <<π，4b =，则以下说法正确的是（ ）A ．3C π=B ．若72c =，则1cos 7B =C ．若sin 2cos sin A B C =，则ABC 是等边三角形D ．若ABC 的面积是43．已知ABC 的面积为3，在ABC 所在的平面内有两点P ，Q ，满足20PA PC +=，2QA QB =，记APQ 的面积为S ，则下列说法正确的是（ ）A ．//PB CQ B ．2133BP BA BC =+ C ．0PA PC ⋅<D ．2S =4．已知在平面直角坐标系中，点()10,1P ，()24,4P .当P 是线段12PP 的一个三等分点时，点P 的坐标为（ ） A ．4,23⎛⎫⎪⎝⎭B ．4,33⎛⎫⎪⎝⎭C ．()2,3D ．8,33⎛⎫ ⎪⎝⎭5．在ABC ∆中,内角,,A B C 的对边分别为,,,a b c 若,2,6A a c π===则角C 的大小是( ) A ．6π B ．3π C ．56π D ．23π 6．已知点()4,6A ，33,2B ⎛⎫- ⎪⎝⎭，与向量AB 平行的向量的坐标可以是（ ） A ．14,33⎛⎫⎪⎝⎭B ．97,2⎛⎫ ⎪⎝⎭C ．14,33⎛⎫-- ⎪⎝⎭D ．(7，9)7．ABC 中，4a =，5b =，面积S =c =（ ）A BC D ．8．已知M 为ABC 的重心，D 为BC 的中点，则下列等式成立的是（ ） A ．1122AD AB AC =+ B ．0MA MB MC ++= C ．2133BM BA BD =+ D ．1233CM CA CD =+9．已知平行四边形的三个顶点的坐标分别是(3,7),(4,6),(1,2)A B C -．则第四个顶点的坐标为（ ） A ．(0,1)- B ．(6,15)C ．(2,3)-D ．(2,3)10．给出下面四个命题，其中是真命题的是（ ）A ．0ABBA B ．AB BC AC C ．AB AC BC += D ．00AB +=11．设,a b 是两个非零向量，则下列描述正确的有（ ） A ．若||||||a b a b +=-，则存在实数λ使得a b λ= B ．若a b ⊥，则||||a b a b +=-C ．若||||||a b a b +=+，则a 在b 方向上的投影为||bD ．若存在实数λ使得a b λ=，则||||||a b a b +=-12．点P 是ABC ∆所在平面内一点,满足20PB PC PB PC PA --+-=,则ABC ∆的形状不可能是( ) A ．钝角三角形B ．直角三角形C ．等腰三角形D ．等边三角形13．已知ABC ∆的面积为32,且2,b c ==,则A =( ) A ．30°B ．60°C ．150°D ．120°14．已知,a b 为非零向量,则下列命题中正确的是( ) A ．若a b a b +=+,则a 与b 方向相同 B ．若a b a b +=-,则a 与b 方向相反 C ．若a b a b +=-,则a 与b 有相等的模D ．若a b a b -=-,则a 与b 方向相同15．题目文件丢失！二、平面向量及其应用选择题16．在△ABC 中，M 是BC 的中点．若AB ＝a ，BC ＝b ，则AM ＝( ) A ．1()2a b + B ．1()2a b - C ．12a b + D ．12a b +17．已知两不共线的向量()cos ,sin a αα=，()cos ,sin b ββ=，则下列说法一定正确的是（ ）A ．a 与b 的夹角为αβ-B ．a b ⋅的最大值为1C ．2a b +≤D ．()()a b a b +⊥-18．O 为ABC ∆内一点内角A 、B 、C 所对的边分别为a 、b 、c ，已知0a OA b OB c OC ⋅+⋅+⋅=，且tan tan tan 0A OA B OB C OC ⋅+⋅+⋅=，若3a =，则边BC 所对的ABC ∆外接圆的劣弧长为（ ） A ．23π B ．43π C ．6π D ．3π 19．若△ABC 中，2sin()sin()sin A B A B C +-=，则此三角形的形状是（ ） A ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形20．三角形ABC 所在平面内一点P 满足PA PB PB PC PC PA ⋅=⋅=⋅，那么点P 是三角形ABC 的（ ） A ．重心 B ．垂心C ．外心D ．内心21．ABC ∆内有一点O ，满足3450OA OB OC ++=，则OBC ∆与ABC ∆的面积之比为（ ） A ．1:4B ．4:5C ．2:3D ．3:522．在ABC 中，AD 、BE 、CF 分别是BC 、CA 、AB 上的中线，它们交于点G ，则下列各等式中不正确．．．的是（ ） A ．23BG BE = B ．2CG GF = C ．12DG AG =D ．0GA GB GC ++=23．在ABC 中，若()()0CA CB CA CB +⋅-=，则ABC 为（ ） A ．正三角形B ．直角三角形C ．等腰三角形D ．无法确定24．在ABC ∆中，E ，F 分别为AB ，AC 的中点，P 为EF 上的任一点，实数x ，y 满足0PA xPB yPC ++=，设ABC ∆、PBC ∆、PCA ∆、PAB ∆的面积分别为S 、1S 、2S 、3S ，记ii S Sλ=（1,2,3i =），则23λλ⋅取到最大值时，2x y +的值为（ ） A ．－1B ．1C ．32-D ．3225．如图，ADC 是等边三角形，ABC 是等腰直角三角形，90ACB ∠︒＝，BD 与AC 交于E 点.若2AB =，则AE 的长为（ ）A ．62-B ．1(62)2- C ．62+D ．1(62)2+26．题目文件丢失！27．如图，为测得河对岸塔AB 的高，先在河岸上选一点C ，使C 在塔底B 的正东方向上，测得点A 的仰角为60°，再由点C 沿北偏东15°方向走10m 到位置D ，测得45BDC ∠=︒，则塔AB 的高是（单位：m ）（ ）A ．2B ．106C ．103D ．1028．设(),1A a ，()2,1B -，()4,5C 为坐标平面上三点，O 为坐标原点，若OA 与OB 在OC 方向上的投影相同，则a =（ ）A ．12-B ．12C ．-2D ．229．已知D ，E ，F 分别是△ABC 的边BC ，CA ，AB 的中点，且BC a CA b ==，，AB c =，则①AD ＝－b －12a ；②BE ＝a ＋12b ；③CF ＝－12a ＋12b ；④AD ＋BE ＋CF ＝0.其中正确的等式的个数为( ) A ．1 B ．2 C ．3 D ．430．ABC ∆中，22:tan :tan a b A B =，则ABC ∆一定是（ ） A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形D ．等腰或直角三角形31．已知菱形ABCD 边长为2，∠B ＝3π，点P 满足AP ＝λAB ，λ∈R ，若BD ·CP ＝－3，则λ的值为( ) A ．12B ．－12C ．13D ．－1332．在ABC ∆中，8AB =，6AC =，60A ∠=，M 为ABC ∆的外心，若AM AB AC λμ=+，λ、R μ∈，则43λμ+=（ ）A ．34B ．53C ．73D ．8333．ABC 中，内角,,A B C 所对的边分别为,,a b c .若()226,c a b =-+3C π=，则ABC 的面积为（ ）A ．6B ．33C ．33D ．334．设ABC ∆中BC 边上的中线为AD ，点O 满足2AO OD =，则OC =（ ）A ．1233AB AC -+ B ．2133AB AC - C ．1233AB AC -D ．2133AB AC -+ 35．在△ABC 中，M 为BC 上一点，60,2,||4ACB BM MC AM ∠=︒==，则△ABC的面积的最大值为（ ） A ．123B ．63C ．12D ．183【参考答案】***试卷处理标记，请不要删除一、多选题 1．ABC 【分析】作出图形，利用平面向量加、减法法则与正方形的性质可判断A 、B 选项的正误；利用平面向量的减法法则与向量的数乘运算可判断C 选项的正误；利用平面向量的加法法则可判断D 选项的正误. 【详解 解析：ABC 【分析】作出图形，利用平面向量加、减法法则与正方形的性质可判断A 、B 选项的正误；利用平面向量的减法法则与向量的数乘运算可判断C 选项的正误；利用平面向量的加法法则可判断D 选项的正误. 【详解】 如下图所示：对于A 选项，四边形ABCD 为正方形，则BD AC ⊥，a b AB BC AB AD DB -=-=-=，()0a b c DB AC ∴-⋅=⋅=，A 选项正确；对于B 选项，0a b c AB BC AC AC AC +-=+-=-=，则()00a b c a a +-⋅=⋅=，B 选项正确；对于C 选项，a c AB AC CB -=-=，则0a c b CB BC --=-=，则()0a c b a --⋅=，C 选项正确；对于D 选项，2a b c c ++=，222a b c c ∴++==，D 选项错误. 故选：ABC. 【点睛】本题考查平面向量相关命题正误的判断，同时也考查了平面向量加、减法法则以及平面向量数量积的应用，考查计算能力，属于中等题.2．AC 【分析】对于，利用正弦定理可将条件转化得到，即可求出； 对于，利用正弦定理可求得，进而可得；对于，利用正弦定理条件可转化为，结合原题干条件可得，进而求得；对于，根据三角形面积公式求得，利解析：AC 【分析】对于A 2sin sin A C A =，即可求出C ； 对于B ，利用正弦定理可求得sin B ，进而可得cos B ；对于C ，利用正弦定理条件可转化为2cos a c B =，结合原题干条件可得B ，进而求得A B C ==；对于D，根据三角形面积公式求得a ，利用余弦定理求得c ，进而由正弦定理求得R ． 【详解】2sin c A =2sin sin AC A =， 因为sin 0A ≠，故sin 2C =， 因为(0,)2C π∈，则3C π=，故A 正确；若72c =，则由正弦定理可知sinsin c b C B =，则4sin sin 72b B Cc ==因为(0,)B π∈，则1cos 7B =±，故B 错误； 若sin 2cos sin A BC =，根据正弦定理可得2cos a c B =，2sinc A =，即sina A=sin2cosA c B=，所以sin A B=，因为23A B Cππ+=-=，则23A Bπ=-，故2sin()3B Bπ-=，1sin2B B B+=，即1sin cos22B B=，解得tan B=3Bπ=，则3Aπ=，即3A B Cπ===，所以ABC是等边三角形，故C正确；若ABC的面积是1sin2ab C=2a=，由余弦定理可得22212cos416224122c a b ab C=+-=+-⨯⨯⨯=，即c=设三角形的外接圆半径是R，由正弦定理可得24sincRC===，则该三角形外接圆半径为2，故D错误，故选：AC．【点睛】本题考查正余弦定理的应用及同角三角函数的基本关系和两角和与差的三角公式，转化思想，计算能力，属于中档题．3．BCD【分析】本题先确定B是的中点，P是的一个三等分点，判断选项A错误，选项C正确；再通过向量的线性运算判断选项B正确；最后求出，故选项D正确.【详解】解：因为，，所以B是的中点，P是的解析：BCD【分析】本题先确定B是AQ的中点，P是AC的一个三等分点，判断选项A错误，选项C正确；再通过向量的线性运算判断选项B正确；最后求出2APQS=△，故选项D正确.【详解】解：因为20PA PC+=，2QA QB=，所以B 是AQ 的中点，P 是AC 的一个三等分点，如图：故选项A 错误，选项C 正确；因为()121333BP BA AP BA BC BA BA BC =+=+-=+，故选项B 正确； 因为112223132APQ ABCAB hS S AB h ⨯⨯==⋅△△，所以，2APQ S =△，故选项D 正确. 故选：BCD 【点睛】本题考查平面向量的线性运算、向量的数量积、三角形的面积公式，是基础题.4．AD 【分析】设，则，然后分点P 靠近点，靠近点两种情况，利用平面向量的线性运算求解. 【详解】 设，则，当点P 靠近点时，， 则， 解得， 所以，当点P 靠近点时，， 则， 解得， 所以， 故选：解析：AD 【分析】设(),P x y ，则()()12,1,4,4=-=--PP x y PP x y ，然后分点P 靠近点1P ，靠近点2P 两种情况，利用平面向量的线性运算求解. 【详解】设(),P x y ，则()()12,1,4,4=-=--PP x y PP x y ， 当点P 靠近点1P 时，1212PPPP =， 则()()1421142x x y y ⎧=-⎪⎪⎨⎪-=-⎪⎩，解得432x y ⎧=⎪⎨⎪=⎩，所以4,23P ⎛⎫⎪⎝⎭， 当点P 靠近点2P 时，122PP PP =， 则()()24124x x y y ⎧=-⎪⎨-=-⎪⎩， 解得833x y ⎧=⎪⎨⎪=⎩，所以8,33P ⎛⎫ ⎪⎝⎭， 故选：AD 【点睛】本题主要考查平面向量的线性运算，还考查了运算求解的能力，属于基础题.5．BD 【分析】由正弦定理可得,所以,而,可得,即可求得答案. 【详解】 由正弦定理可得, ,而, , , 故或. 故选:BD. 【点睛】本题考查了根据正弦定理求解三角形内角,解题关键是掌握解析：BD【分析】由正弦定理可得sin sin a c A C =,所以sin sin c C A a ==,而a c <,可得A C <,即可求得答案. 【详解】 由正弦定理可得sin sin a cA C=,∴ sin sin c C A a ==而a c <,∴ A C <, ∴566C ππ<<, 故3C π=或23π. 故选:BD. 【点睛】本题考查了根据正弦定理求解三角形内角,解题关键是掌握正弦定理和使用正弦定理多解的判断,考查了分析能力和计算能力,属于中等题.6．ABC 【分析】先求出向量的坐标，然后由向量平行的条件对选项进行逐一判断即可. 【详解】 由点，，则选项A . ,所以A 选项正确. 选项B. ,所以B 选项正确. 选项C . ,所以C 选解析：ABC 【分析】先求出向量AB 的坐标，然后由向量平行的条件对选项进行逐一判断即可. 【详解】由点()4,6A ，33,2B ⎛⎫- ⎪⎝⎭，则972，AB ⎛⎫=-- ⎪⎝⎭选项A . 91473023⎛⎫-⨯--⨯= ⎪⎝⎭,所以A 选项正确. 选项B. 9977022⎛⎫-⨯--⨯= ⎪⎝⎭,所以B 选项正确. 选项C . ()91473023⎛⎫⎛⎫-⨯---⨯-= ⎪ ⎪⎝⎭⎝⎭,所以C 选项正确.选项D. 979702⎛⎫-⨯--⨯≠ ⎪⎝⎭,所以选项D 不正确 故选：ABC【点睛】 本题考查根据点的坐标求向量的坐标，根据向量的坐标判断向量是否平行，属于基础题.7．AB【分析】在中，根据，，由，解得或，然后分两种情况利用余弦定理求解.【详解】中，因为，，面积，所以，所以，解得或，当时，由余弦定理得：，解得，当时，由余弦定理得：，解得所以或解析：AB【分析】在ABC 中，根据4a =，5b =，由1sin 2ABC S ab C ==60C =或120C =，然后分两种情况利用余弦定理求解.【详解】ABC 中，因为4a =，5b =，面积ABC S =所以1sin 2ABC S ab C ==所以sin C =60C =或120C =， 当60C =时，由余弦定理得：2222cos 21c a b ab C =+-=，解得c =当120C =时，由余弦定理得：2222cos 61c a b ab C =+-=，解得c =所以c =c =故选：AB【点睛】本题主要考查三角形面积公式和余弦定理的应用，还考查了运算求解的能力，属于中档题. 8．ABD【分析】根据向量的加减法运算法则依次讨论即可的答案.【详解】解：如图，根据题意得为三等分点靠近点的点.对于A 选项，根据向量加法的平行四边形法则易得，故A 正确；对于B 选项，，由于为三解析：ABD【分析】根据向量的加减法运算法则依次讨论即可的答案.【详解】解：如图，根据题意得M 为AD 三等分点靠近D 点的点.对于A 选项，根据向量加法的平行四边形法则易得1122AD AB AC =+，故A 正确；对于B 选项，2MB MC MD +=，由于M 为AD 三等分点靠近D 点的点，2MA MD =-，所以0MA MB MC ++=，故正确；对于C 选项，()2212=3333BM BA AD BA BD BA BA BD =+=+-+，故C 错误；对于D 选项，()22123333CM CA AD CA CD CA CA CD =+=+-=+，故D 正确.故选：ABD【点睛】本题考查向量加法与减法的运算法则，是基础题.9．ABC【分析】设平行四边形的四个顶点分别是，分类讨论点在平行四边形的位置有：，，，将向量用坐标表示，即可求解.【详解】第四个顶点为，当时，，解得，此时第四个顶点的坐标为；当时，，解得解析：ABC【分析】设平行四边形的四个顶点分别是(3,7),(4,6),(1,2),(,)A B C D x y -，分类讨论D 点在平行四边形的位置有：AD BC =，AD CB =，AB CD =，将向量用坐标表示，即可求解.【详解】第四个顶点为(,)D x y ，当AD BC =时，(3,7)(3,8)x y --=--，解得0,1x y ==-，此时第四个顶点的坐标为(0,1)-；当AD CB =时，(3,7)(3,8)x y --=，解得6,15x y ==，此时第四个顶点的坐标为(6,15)；当AB CD =时，(1,1)(1,2)x y -=-+，解得2,3x y ==-，此时第四个项点的坐标为(2,3)-．∴第四个顶点的坐标为(0,1)-或(6,15)或(2,3)-．故选:ABC .【点睛】本题考查利用向量关系求平行四边形顶点坐标，考查分类讨论思想，属于中档题.10．AB【解析】【分析】根据向量加法化简即可判断真假.【详解】因为，正确；，由向量加法知正确；，不满足加法运算法则，错误；，所以错误.故选：A B.【点睛】本题主要考查了向量加法的解析：AB【解析】【分析】根据向量加法化简即可判断真假.【详解】因为0AB BA AB AB ，正确；AB BC AC ，由向量加法知正确；AB AC BC +=，不满足加法运算法则，错误；0,AB AB +=，所以00AB +=错误.故选：A B .【点睛】本题主要考查了向量加法的运算，属于容易题.11．AB【分析】若，则反向，从而；若，则，从而可得；若，则同向，在方向上的投影为若存在实数使得，则共线，但是不一定成立.【详解】对于选项A ，若，则反向，由共线定理可得存在实数使得；对于选解析：AB【分析】若||||||a b a b +=-，则,a b 反向，从而a b λ=；若a b ⊥，则0a b ⋅=，从而可得||||a b a b +=-；若||||||a b a b +=+，则,a b 同向，a 在b 方向上的投影为||a若存在实数λ使得a b λ=，则,a b 共线，但是||||||a b a b +=-不一定成立.【详解】对于选项A ，若||||||a b a b +=-，则,a b 反向，由共线定理可得存在实数λ使得a b λ=；对于选项B ，若a b ⊥，则0a b ⋅=，222222||2,||2a b a a b b a b a a b b +=+⋅+-=-⋅+,可得||||a b a b +=-；对于选项C ，若||||||a b a b +=+，则,a b 同向，a 在b 方向上的投影为||a ;对于选项D ，若存在实数λ使得a b λ=，则,a b 共线，但是||||||a b a b +=-不一定成立. 故选：AB.【点睛】本题主要考查平面向量的性质及运算，明确向量的性质及运算规则是求解的关键，侧重考查逻辑推理的核心素养.12．AD【分析】由条件可得，再两边平方即可得答案.【详解】∵P 是所在平面内一点，且，∴，即，∴，两边平方并化简得，∴，∴，则一定是直角三角形，也有可能是等腰直角三角形，故解析：AD【解析】【分析】由条件可得||||AB AC AC AB -=+，再两边平方即可得答案.【详解】∵P 是ABC ∆所在平面内一点，且|||2|0PB PC PB PC PA --+-=，∴|||()()|0CB PB PA PC PA --+-=，即||||CB AC AB =+，∴||||AB AC AC AB -=+，两边平方并化简得0AC AB ⋅=，∴AC AB ⊥，∴90A ︒∠=，则ABC ∆一定是直角三角形，也有可能是等腰直角三角形，故不可能是钝角三角形，等边三角形，故选：AD.【点睛】本题考查向量在几何中的应用，考查计算能力，是基础题.13．BD【分析】由三角形的面积公式求出即得解.【详解】因为,所以,所以,因为,所以或120°.【点睛】本题主要考查三角形面积的应用，意在考查学生对这些知识的理解掌握水平. 解析：BD【分析】由三角形的面积公式求出sin A =即得解. 【详解】 因为13sin 22S bc A ==,所以13222A ⨯=,所以sin A =,因为0180A ︒︒<<, 所以60A =或120°.故选：BD【点睛】本题主要考查三角形面积的应用，意在考查学生对这些知识的理解掌握水平. 14．ABD【分析】根据平面向量的平行四边形法则与三角不等式分析即可.【详解】如图,根据平面向量的平行四边形或三角形法则,当不共线时,根据三角形两边之和大于第三边,两边之差小于第三边有.当同向时解析：ABD【分析】根据平面向量的平行四边形法则与三角不等式分析即可.【详解】如图,根据平面向量的平行四边形或三角形法则,当,a b 不共线时,根据三角形两边之和大于第三边,两边之差小于第三边有||||||||||||a b a b a b -<±<+.当,a b 同向时有||||||a b a b +=+,||||||a b a b -=-.当,a b 反向时有||||||||a b a b +=-,||+||||a b a b =-故选：ABD【点睛】本题主要考查了平面向量的线性运算与三角不等式,属于基础题型.15．无二、平面向量及其应用选择题16．D【分析】根据向量的加法的几何意义即可求得结果.【详解】在ABC ∆中，M 是BC 的中点，又,AB a BC b ==， 所以1122AM AB BM AB BC a b =+=+=+， 故选D.【点睛】该题考查的是有关向量的问题，涉及到的知识点有向量的加法运算，属于简单题目. 17．D【分析】由向量夹角的范围可判断A 选项的正误；计算出a b ⋅，利用余弦函数的值域以及已知条件可判断B 选项的正误；利用平面向量模的三角不等式可判断C 选项的正误；计算()()a b a b +⋅-的值可判断D 选项的正误.综合可得出结论.【详解】()cos ,sin a αα=，()cos ,sin b ββ=，则22cos sin 1a αα=+=，同理可得1b =，a 与b 不共线，则()sin cos cos sin sin 0αβαβαβ-=-≠，则()k k Z αβπ-≠∈. 对于A 选项，由题意知，a 与b 的夹角的范围为()0,π，而()R αβ-∈且()k k Z αβπ-≠∈，A 选项错误；对于B 选项，设向量a 与b 的夹角为θ，则0θπ<<，所以，()cos cos 1,1a b a b θθ⋅=⋅=∈-，B 选项错误；对于C 选项，由于a 与b 不共线，由向量模的三角不等式可得2a b a b +<+=，C 选项错误；对于D 选项，()()22220a b a b a b a b +⋅-=-=-=，所以，()()a b a b +⊥-，D 选项正确.故选：D.【点睛】本题考查平面向量有关命题真假的判断，涉及平面向量的夹角、数量积与模的计算、向量垂直关系的处理，考查运算求解能力与推理能力，属于中等题.18．A【分析】根据题意得出tan tan tan A B C a b c==，利用正弦定理边化角思想和切化弦思想得出A B C ==，从而可得知ABC ∆为等边三角形，进而可求得BC 所对的ABC ∆外接圆的劣弧长.【详解】0a OA b OB c OC ⋅+⋅+⋅=，a b OC OA OB c c∴=--， 同理可得tan tan tan tan A B OC OA OB C C =--，tan tan tan tan a A c C b B cC ⎧-=-⎪⎪∴⎨⎪-=-⎪⎩，tan tan tan A B C a b c∴==， 由正弦定理得tan tan tan sin sin sin A B C A B C ==，所以，111cos cos cos A B C==， cos cos cos A B C ∴==， 由于余弦函数cos yx =在区间()0,π上单调递减，所以，3A B C π===， 设ABC ∆的外接圆半径为R ，则22sin a R A===，1R ∴=， 所以，边BC 所对的ABC ∆外接圆的劣弧长为222133R A ππ⨯=⨯=. 故选：A.本题考查弧长的计算，涉及正弦定理边角互化思想、切化弦思想以及正弦定理的应用，考查计算能力，属于中等题.19．A【分析】已知等式左边第一项利用诱导公式化简，根据sin C 不为0得到sin()sin A B C -=，再利用两角和与差的正弦函数公式化简.【详解】ABC ∆中，sin()sin A B C +=，∴已知等式变形得：2sin sin()sin C A B C -=，即sin()sin sin()A B C A B -==+， 整理得：sin cos cos sin sin cos cos sin A B A B A B A B -=+，即2cos sin 0A B =， cos 0A ∴=或sin 0B =（不合题意，舍去），0A π<<90A ∴=︒，则此三角形形状为直角三角形．故选：A【点睛】此题考查了正弦定理，以及三角函数中的恒等变换应用，熟练掌握公式是解本题的关键，属于中档题．20．B【分析】先化简得0,0,0PA CB PB CA PC AB ⋅=⋅=⋅=，即得点P 为三角形ABC 的垂心.【详解】由于三角形ABC 所在平面内一点P 满足PA PB PB PC PC PA ⋅=⋅=⋅，则()()()0,0,0PA PB PC PB PA PC PC PB PA ⋅-=⋅-=⋅-=即有0,0,0PA CB PB CA PC AB ⋅=⋅=⋅=，即有,,PA CB PB CA PC AB ⊥⊥⊥，则点P 为三角形ABC 的垂心.故选：B.【点睛】本题主要考查向量的运算和向量垂直的数量积，意在考查学生对这些知识的理解掌握水平. 21．A【解析】分析：由题意，在ABC ∆内有一点O ，满足3450++=OA OB OC ，利用三角形的奔驰定理，即可求解结论．详解：由题意，在ABC ∆内有一点O ，满足3450++=OA OB OC ，由奔驰定理可得::3:4:5BOC AOC BOA S S S ∆∆∆=，所以:3:121:4BOC ABC S S ∆∆==，点睛：本题考查了向量的应用，对于向量的应用问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用，利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．22．C【分析】由三角形的重心定理和平面向量的共线定理可得答案．【详解】 ABC 中，AD 、BE 、CF 分别是BC 、CA 、AB 上的中线，它们交于点G ，可得G 为重心，则23BG BE =，2CG GF =，12DG GA =且0GA GB GC ++= 故选：C【点睛】本题考查了三角形的重心定理和向量共线定理，属于中档题．23．C【分析】利用平面向量的数量积的运算性质可得(CA CB + 2222)()0CA CB CA CB b a -=-=-=，从而可得答案．【详解】 解：在ABC 中，(CA CB + 2222)()0CA CB CA CB b a -=-=-=， a b ∴=，ABC ∴为等腰三角形，故选：C ．【点睛】本题考查三角形形状的判断，考查向量的数量积的运算性质，属于中档题．24．D【分析】根据三角形中位线的性质，可得P 到BC 的距离等于△ABC 的BC 边上高的一半，从而得到12312S S S S ==+，由此结合基本不等式求最值，得到当23λλ⋅取到最大值时，P 为EF 的中点，再由平行四边形法则得出11022PA PB PC ++=，根据平面向量基本定理可求得12x y ==，从而可求得结果. 【详解】如图所示：因为EF 是△ABC 的中位线，所以P 到BC 的距离等于△ABC 的BC 边上高的一半， 所以12312S S S S ==+， 由此可得22232322322()1216S S S S S S S S S S λλ+=⨯=≤=， 当且仅当23S S =时，即P 为EF 的中点时，等号成立，所以0PE PF +=，由平行四边形法则可得2PA PB PE +=，2PA PC PF +=，将以上两式相加可得22()0PA PB PC PE PF ++=+=， 所以11022PA PB PC ++=， 又已知0PA xPB yPC ++=， 根据平面向量基本定理可得12x y ==， 从而132122x y +=+=. 故选：D【点睛】本题考查了向量加法的平行四边形法则，考查了平面向量基本定理的应用，考查了基本不等式求最值，属于中档题.25．A【分析】由条件求得∠BCD ＝150°，∠CBE ＝15°，故∠ABE ＝30°，可得∠AEB ＝105°．计算sin105°，代入正弦定理sin30sin105AE AB =︒︒，化简求得AE 62=-． 【详解】由题意可得，AC ＝BC ＝CD ＝DA 2=BAC ＝45°，∠BCD ＝∠ACB +∠ACD ＝90°+60°＝150°．又△BCD 为等腰三角形，∴∠CBE ＝15°，故∠ABE ＝45°﹣15°＝30°，故∠BEC ＝75°，∠AEB ＝105°．再由 sin105°＝sin （60°+45°）＝sin60°cos45°+cos60°sin45°62+=，△ABE 中，由正弦定理可得sin30sin105AE AB =︒︒，∴12AE =，∴AE =）， 故选:A ．【点睛】本题考查勾股定理、正弦定理的应用，两角和的正弦公式，属于中档题．26．无27．B【分析】设塔高为x 米，根据题意可知在△ABC 中，∠ABC=90°，∠ACB=60°，AB=x ，从而有x ，在△BCD 中，CD=10，∠BCD=105°，∠BDC=45°，∠CBD=30°，由正弦定理可求 BC ，从而可求x 即塔高．【详解】设塔高为x 米，根据题意可知在△ABC 中，∠ABC=90°，∠ACB=60°，AB=x ，从而有x ，x ， 在△BCD 中，CD=10，∠BCD=60°+30°+15°=105°，∠BDC=45°，∠CBD=30° 由正弦定理可得，sin sin BC CD BDC CBD = 可得，BC=10sin 45sin 303x ==. 则；所以塔AB 的高是米；故选B ．【点睛】本题主要考查了正弦定理在实际问题中的应用，解决本题的关键是要把实际问题转化为数学问题，即正确建立数学模型，结合已知把题目中的数据转化为三角形中的数据，进而选择合适的公式进行求解．28．A【分析】根据平面向量的投影的概念，结合向量的数量积的运算公式，列出方程，即可求解.【详解】由题意，点(),1A a ，()2,1B -，()4,5C ， O 为坐标原点，根据OA 与OB 在OC 方向上的投影相同，则OA OC OB OCOC OC ⋅⋅=, 即OA OC OB OC ⋅=⋅，可得4152415a +⨯=⨯-⨯，解得12a =-. 故选：A. 【点睛】 本题主要考查了平面向量的数量积的坐标运算，以及向量的投影的定义，其中解答中熟记向量投影的定义，以及向量的数量积的运算公式，列出方程是解答的关键，着重考查运算与求解能力.29．D【分析】 本题考查的知识点是向量的加减法及其几何意义、及零向量，我们根据已知中的图形，结合向量加减法的三角形法则，对题目中的四个结论逐一进行判断，即可得到答案．【详解】①如图可知AD ＝AC ＋CD ＝AC ＋12CB ＝－CA －12BC ＝－b －12a ，故①正确． ②BE ＝BC ＋CE ＝BC ＋12CA ＝a ＋12b ，故②正确． ③CF ＝CA ＋AE ＝CA ＋12AB ＝b ＋12(－a －b ) ＝－12a ＋12b ，故③正确． ④AD ＋BE ＋CF ＝－DA ＋BE ＋CF＝－(DC ＋CA )＋BE ＋CF＝－(12a ＋b )＋a ＋12b －12a ＋12b ＝0，故④正确． 故选D.【点睛】 本题考查的主要知识点是向量加减法及其几何意义，关键是要根据向量加减法及其几何意义，将未知的向量分解为已知向量．30．D【分析】由已知22:tan :tan a b A B =，利用正弦定理及同角的三角函数的基本关系对式子进行化简，然后结合三角函数的性质再进行化简即可判断．【详解】∵22:tan :tan a b A B =， 由正弦定理可得，22sin sin tan sin cos sin sin sin tan sin cos cos AA A AB B B B B B AB===， ∵sin sin B 0A ≠， ∴sin cos sin cos A B B A=， ∴sin cos sin cos A A B B =即sin 2sin 2A B =，∵()(),0,,0,A B A B ππ∈+∈， ∴22A B =或22A B π+=，∴A B =或2A B π+=，即三角形为等腰或直角三角形， 故选D ．【点睛】本题考查同角三角函数的基本关系及正弦定理的应用，利用正弦定理进行代数式变形是解题的关键和难点．31．A【分析】根据向量的基本定理，结合数量积的运算公式，建立方程即可得到结论．【详解】法一：由题意可得BA ·BC ＝2×2cos 3π＝2， BD ·CP ＝(BA ＋BC )·(BP －BC ) ＝(BA ＋BC )·[(AP －AB )－BC ] ＝(BA ＋BC )·[(λ－1)·AB －BC ] ＝(1－λ) BA 2－BA ·BC ＋(1－λ)·BA ·BC －BC 2＝(1－λ)·4－2＋2(1－λ)－4 ＝－6λ＝－3，∴λ＝12，故选A. 法二：建立如图所示的平面直角坐标系，则B (2,0)，C (1，)，D (－1，3)． 令P (x,0)，由BD ·CP ＝(－3，3)·(x －1，－3)＝－3x ＋3－3＝－3x ＝－3得x ＝1. ∵AP ＝λAB ，∴λ＝12.故选A. 【点睛】1.已知向量a ，b 的坐标，利用数量积的坐标形式求解．设a ＝(a 1，a 2)，b ＝(b 1，b 2)，则a ·b ＝a 1b 1＋a 2b 2. 2.通过建立平面直角坐标系，利用数量积的坐标形式计算.32．C【分析】作出图形，先推导出212AM AB AB ⋅=，同理得出212AM AC AC ⋅=，由此得出关于实数λ、μ的方程组，解出这两个未知数的值，即可求出43λμ+的值. 【详解】如下图所示，取线段AB 的中点E ，连接ME ，则AM AE EM =+且EM AB ⊥，()212AM AB AE EM AB AE AB EM AB AB ∴⋅=+⋅=⋅+⋅=， 同理可得212AM AC AC ⋅=，86cos6024AB AC ⋅=⨯⨯=，由221212AM AB AB AM AC AC ⎧⋅=⎪⎪⎨⎪⋅=⎪⎩，可得()()3218AB AC AB AB AC AC λμλμ⎧+⋅=⎪⎨+⋅=⎪⎩，即642432243618λμλμ+=⎧⎨+=⎩， 解得512λ=，29，因此，52743431293λμ+=⨯+⨯=. 故选：C.【点睛】 本题考查利用三角形外心的向量数量积的性质求参数的值，解题的关键就是利用三角形外心的向量数量积的性质列方程组求解，考查分析问题和解决问题的能力，属于中等题. 33．B【分析】由条件和余弦定理得到6ab =，再根据三角形的面积公式计算结果.【详解】由条件可知：22226c a b ab =+-+，①由余弦定理可知：222222cos c a b ab C a b ab =+-=+-，②所以由①②可知，62ab ab -=-，即6ab =，则ABC 的面积为11333sin 622S ab C ==⨯⨯=. 故选：B【点睛】本题考查解三角形，重点考查转化与化归思想，计算能力，属于基础题型.34．A【分析】作出图形，利用AB 、AC 表示AO ，然后利用平面向量减法的三角形法则可得出OC AC AO =-可得出结果.【详解】如下图所示：D 为BC 的中点，则()1122AD AB BD AB BC AB AC AB =+=+=+-1122AB AC =+， 2AO OD =，211333AO AD AB AC ∴==+，11123333OC AC AO AC AB AC AB AC ⎛⎫∴=-=-+=-+ ⎪⎝⎭， 故选：A.【点睛】本题考查利用基底表示向量，考查了平面向量减法和加法三角形法则的应用，考查计算能力，属于中等题.35．A【分析】由已知条件，令||AC a =，||BC b =，则在△ACM 中结合余弦定理可知48ab ≤，根据三角形面积公式即可求最大值 【详解】 由题意，可得如下示意图令||AC a =，||BC b =，又2BM MC =，即有1||||33b CM CB == ∴由余弦定理知：222||||||2||||cos AM CA CM CA CM ACB =+-∠2221216()332333a ab ab ab ab b =+-⨯≥-=，当且仅当3a b =时等号成立 ∴有48ab ≤∴113sin 4812322ABC S ab C ∆=≤⨯=故选：A【点睛】本题考查了正余弦定理，利用向量的知识判断线段的长度及比例关系，再由余弦定理并应用基本不等式求三角形两边之积的范围，进而结合三角形面积公式求最值。

B .该分子是极性分子 D.该物质难溶于水青岛九中2010— 2011学年度第二学期第一学段模块结业高二年级化学试题命题人：官福荣(1) 考试时间90分钟，为闭卷考试。

不得用计算器进行有关计算。

(2) 将I 卷选择题正确答案涂到答题卡相应的位置上，答在试卷上无效。

(3 )将□卷正确答案答到答题纸相应的位置，答在试卷上不得分。

可能用到的原子量：H:1S:32O:16 Al : 27 Na:23Cl:35.5 Fe:56第I 卷选择题(共48分)一、选择题(每小题只有一个正确答案，每题 3分，共48分)1.1下列有机物的系统命名中正确的是A . 3 —甲基一4—乙基戊烷B . 3, 3, 4—三甲基己烷 C. 3, 4, 4—三甲基己烷 D. 3, 5—二甲基己烷2. 2既能用酸性高锰酸钾溶液鉴别，又能用溴的四氯化碳溶液鉴别的一组物质是A •苯与甲苯B •己烷与苯C.乙烯与乙炔 D •乙烯与乙烷3.3下列晶体熔化：氢氧化钠、二氧化硅、氧化钙、硫单质，需要克服的粒子间的相互作用有：①共价键，②离子键，③分子间作用力。

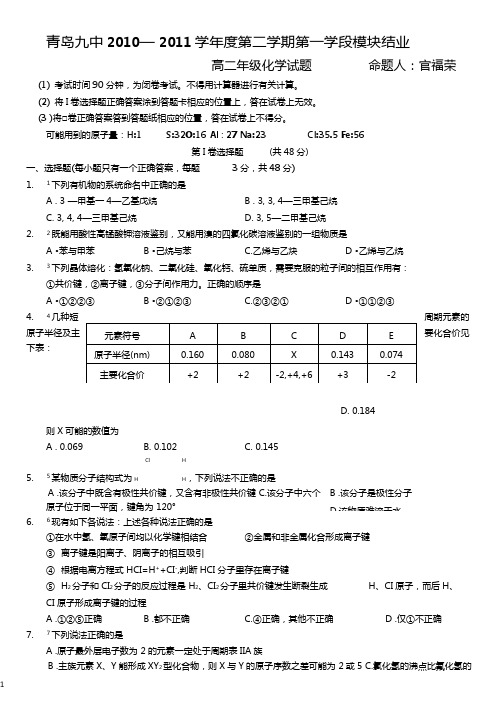
正确的顺序是 A •①②②③ B •②①②③ C.②③②① D •①①②③4.4几种短周期元素的原子半径及主要化合价见下表：则X 可能的数值为 A . 0.069 B. 0.102C. 0.145ClH 5.5某物质分子结构式为HH，下列说法不正确的是A .该分子中既含有极性共价键，又含有非极性共价键 C.该分子中六个原子位于同一平面，键角为 120° 6.6现有如下各说法：上述各种说法正确的是①在水中氢、氧原子间均以化学键相结合 ②金属和非金属化合形成离子键③ 离子键是阳离子、阴离子的相互吸引④ 根据电离方程式 HCI=H ++CI -,判断HCI 分子里存在离子键⑤ H 2分子和CI 2分子的反应过程是 H 2、CI 2分子里共价键发生断裂生成 H 、CI 原子，而后H 、CI 原子形成离子键的过程 A .①②⑤正确 B .都不正确 C.④正确，其他不正确D .仅①不正确7.7下列说法正确的是A .原子最外层电子数为 2的元素一定处于周期表IIA 族B .主族元素X 、Y 能形成XY 2型化合物，则X 与Y 的原子序数之差可能为 2或5 C.氯化氢的沸点比氟化氢的D. 0.184沸点高D .同主族元素形成的氧化物的晶体类型均相同8.8三氯化氮(NCIJ常温是一种淡黄色液体，其分子结构呈三角锥形，关于NCb的说法中正确的是A.它是一种非极性分子B .它能以配位键与CI—结合，生成NCl4—C.其挥发性比PCI3小D .已知NCb中N元素为一3价，所以NCb水解产物为NH3和HCIO(1) A •图⑴和图⑶ A . O 22+和 N 2B . O 3 和 SO 2 14.14元素X 、Y 、Z 原子序数之和为36, X 、 构。

山东省青岛市第九中学高二数学理上学期期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知是R上的单调增函数，则的取值范围是（）A. B. C. D.参考答案：D略2. 在200米高的山顶上，测得山下一塔顶与塔底的俯角分别为30°、60°，则塔高为（）A 米B 米C 200米D 200米参考答案：A3. 若x∈R，则“x＞1”是“＜1”的（）A．充分非必要条件B．必要非充分条件C．充要条件D．既非充分也非必要条件参考答案：A【分析】根据充分必要条件的定义判断即可．【解答】解：由x＞1，一定能得到得到＜1，但当＜1时，不能推出x＞1 （如x=﹣1时），故x＞1是＜1 的充分不必要条件，故选：A．4. 在某项体育比赛中，七位裁判为一选手打出的分数如下：93，89，92，95，93，94，93，去掉一个最高分和一个最低分后，所剩数据的平均值和方差为（）A．92，2 B．92，2.8 C．93，2 D．93，0.4参考答案：D【考点】极差、方差与标准差．【分析】根据所给的条件，看出七个数据，根据分数处理方法，去掉一个最高分95和一个最低分89后，把剩下的五个数字求出平均数和方差．【解答】解：由题意知，去掉一个最高分95和一个最低分89后，所剩数据93，92，93，94，93的平均数为=93；方差为 [（93﹣93）2+（92﹣93）2+（93﹣93）2+（94﹣93）2+（93﹣93）2]=0.4，故选：D．5. 抛物线的准线方程为（）A．B．C．D．参考答案：B6. 过椭圆(θ为参数)的右焦点F作直线l交C于M，N两点，，则的值为()A. B. C. D. 不能确定参考答案：B【分析】先写出椭圆的直角坐标方程和直线l的参数方程，把直线l的参数方程代入椭圆的方程化简整理，再利用直线参数方程t的几何意义解答.【详解】曲线C为椭圆，右焦点为F(1，0)，设l：(t为参数)，代入椭圆方程得(3＋sin2θ)t2＋6tcos θ－9＝0，设M、N两点对应的参数分别为t1，t2，则t1t2＝－，t1＋t2＝－，所以.故答案为：B.【点睛】(1)本题主要考查参数方程和直角坐标方程的互化，考查直线的参数方程和t的几何意义，考查直线和椭圆的位置关系，意在考查学生对这些知识的掌握水平和分析推理计算能力.(2)过定点、倾斜角为的直线的参数方程（为参数）.当动点在定点上方时,. 当动点在定点下方时,.7. 用反证法证明命题“若自然数a，b，c的积为偶数，则a，b，c中至少有一个偶数”时，对结论正确的反设为（）A. a，b，c中至多有一个偶数B. a，b，c都是奇数C. a，b，c至多有一个奇数D. a，b，c都是偶数参考答案：B“至少有一个偶数”的对立面是“没有偶数”，故选B.8. 如图，某几何体的正视图和俯视图都是矩形，侧视图是平行四边形，则该几何体的体积为（）A ． B．C ．D ．参考答案：B略9.方程表示的曲线是 ( )A.两条射线和一个圆B.一条直线和一个圆C.一条射线和一个半圆D.两条射线和一个半圆参考答案：A略10. “”是“”的（）A．充分不必要条件 B．必要不充分条件 C．充要条件D．既不充分也不必要条件参考答案：A略二、填空题:本大题共7小题,每小题4分,共28分11. 已知是圆（为圆心）上一动点，线段的垂直平分线交直线于，则动点的轨迹方程为．参考答案：12. 已知函数f（x）=|x2+2x﹣1|，若a＜b＜﹣1，且f（a）=f（b），则ab+a+b的取值范围是_________ ．参考答案：（-1,1）13. 如图，梯形ABCD中，AD∥BC，∠ABC=90°，对角线AC⊥BD于P点，已知AD∶BC=1∶2，则BD∶AC的值是__________.参考答案：14. 以下结论正确的是（1）根据2×2列联表中的数据计算得出2≥6.635, 而P（2≥6.635）≈0.01，则有99% 的把握认为两个分类变量有关系。

青岛市高二数学知识点在高二数学学习过程中，学生需要掌握许多数学知识点。

下面将对一些重要的数学知识点进行详细介绍。

1. 一次函数与二次函数一次函数和二次函数是高中数学中常见的函数类型。

一次函数的形式为y=ax+b，其中a和b为常数，a决定了函数的斜率，b决定了函数与y轴的截距。

而二次函数的形式为y=ax^2+bx+c，其中a、b、c为常数，a决定了函数的开口方向，b决定了函数的对称轴位置，c决定了函数与y轴的截距。

2. 概率与统计概率与统计是数学中的一个重要分支。

通过概率与统计的学习，我们能够了解到随机现象的规律性。

概率是研究事件发生的可能性，统计是从已知数据中进行推断和预测。

在概率与统计中，我们需要了解一些重要的概念，如样本空间、事件、频率、概率分布等。

3. 数列与数列极限数列是由一连串有序数排成的序列。

数列的极限是数列中的数随着项数的增加趋向于的确定值。

在数列的学习中，我们需要掌握数列的通项公式、等差数列和等比数列的性质，以及数列极限的计算方法和极限存在的条件等。

4. 导数与微分导数是函数在某一点上的变化率。

通过导数的计算，我们可以求出函数的切线斜率、函数的极值点和函数的增减性。

微分是导数的应用之一，通过微分我们可以求出函数在某一点的近似值，帮助我们进行函数的近似计算和问题的求解。

5. 三角函数三角函数是研究角度和边长之间关系的数学工具。

常见的三角函数有正弦函数、余弦函数和正切函数等。

三角函数具有周期性和对称性的特点，在解决角度问题和三角函数方程时起到重要的作用。

6. 矩阵与行列式矩阵是数学中的一种重要工具，可以用来描述线性变换等问题。

矩阵的运算包括加法、减法、数乘和乘法等。

行列式是矩阵的一个特殊性质，可以用来判断矩阵的可逆性和求解线性方程组等问题。

以上是高二数学中的一些重要知识点，掌握了这些知识点，学生将能够更好地应对高中数学学习中的各类问题和考试。

在学习数学的过程中，除了掌握基本的概念和计算方法外，还要注重理解与实际应用的结合，通过解决实际问题来提高数学能力。

青岛九中高二下期中考试数学试题山东名校考试联盟2023-2024 学年高二年级下学期期中检测数学试题参考答案2024.05一、选择题: 本题共 8 小题, 每小题 5 分, 共 40 分。

在每小题给出的四个选项中, 只有一个选项是符合题目要求的。

题号12345678答案D A C B D D C A1. 设函数 f (x ) 在 x =x 0 处的导数为 2,则 lim Δx→0f (x 0+2Δx )−f (x 0)Δx=（ ）A. 12 B. 1 C. 2 D. 4【解析】 limΔx→0f (x 0+2Δx )−f (x 0)Δx=2limΔx→0f (x 0+2Δx )−f (x 0)2Δx=2lim2Δx→0f (x 0+2Δx )−f (x 0)2Δx=2f ′(x 0)=4 ,故选 D2. 个位数大于十位数的两位数共有（ ）个A. 36 B. 40 C. 42 D. 56【解析】个位数大于十位数的两位数个位数显然不能为 0 , 故只需在 1-9 九个数字中选两个,大的在个位,小的在十位即可,故共有 C 29=36 种可能,故选 A 3. 已知函数 f (x ) 的导函数 f ′(x ) 的图象如图所示,则 f (x ) 的图象可能为（ ）【解析】由导函数图像可知原函数应是先增后减再增的,故在 B 、C 中选择,随着 x 的增大, 导函数越来越大, 故原函数增长越来越快, 应选 C 4. 已知函数 f (x )=12x 2−f ′(1)x +ln x ,则 f ′(1)=（ ）A. −32 B. 1 C. 32 D. 2【解析】 f ′(x )=x−f ′(1)+1x ,将 x =1 带入可得 f ′(1)=1−f ′(1)+11 ,解得 f ′(1)=1 ,故选 B5.(y +x 2y)(x +y )6 的展开式中 x 3y 4 的系数为（ ）A. 6B. 20C. 21D. 26【解析】 (y+x2y)(x +y )6=y (x +y )6+x 2y (x+y )6 其中含 x 3y 4 的项为 yC 36x 3y 3+x 2y C 56xy 5,x 3y4 的系数为 C 36+C 56=26 故选 D6. 书架上已有四本书, 小明又带来了两本不同的长篇小说和一本人物传记要放到书架上, 若两本小说不能放到一起, 则不同的放法有 ( ) 种A. 30 B. 90 C. 120 D. 150【解析】人物传记有 5 种放法, 这样五本书之间有 6 个空, 两本不同的长篇小说选两个空插入即可不相邻,共有 5 A 26=150 种方法,故选 D7. 已知 a =A 2020,b =1020,c =C 2040 ,则（ ）A. a <b <cB. c <b <aC. c <a <bD. b <c <a【解析】 a =20×19×18×⋯×2×1,b =10×10×10×⋯×10×10 ,均由 20 个数相乘组成,其中前两项和最后一项比较 20×19×1<10×10×10 ,其他项 18×2<10×10,17×3<10×10 直到 11×9<10×10 ,故 a <b ,c =40×39×38×⋯×22×2120×19×18×⋯×2×1<2×310×43×52×6×8×11×21 ,其中 a =20×19×18×⋯×2×1 里面前四项大于 2×310×43×52×6×8×11×21 中的后五项,即 20×19×18×17>5×6×8×11×21 ,其他项均要对应大于或等于剩余 2×310×43×5 中的每一项, 故 c <a ,故选 C8. 已知曲线 y =x ln x 过点 (0,−1) 的切线与函数 y =ax 2+(a +2)x 的图象只有一个公共点, 则 a 的值为（ ）A. 0 或 1 B. 0 或 12 C. 12 D. 1【解析】设切线与曲线y=x ln x的切点为(x0,x0ln x0) ,函数y=x ln x的导函数为y′=ln x+1 , 故y′=ln x0+1=x0ln x0+1x0,解得x0=1 ,故切线方程为y=x−1 ,当a=0时, y=ax2+(a+2)x=2x ,显然成立,当a≠0时, y=ax2+(a+2)x与y=x−1联立, ax2+(a+1)x+1=0 ,其中Δ= (a+1)2−4a=0 , 解得a=1 ,故选A二、选择题: 本题共 3 小题, 每小题 6 分, 共 18 分。

青岛九中2014年暑假高二数学微课学案 2.3.1直线与平面垂直的判定一、核心知识1、直线与平面垂直的概念和判定定理直线与平面垂直的定义： ______________________________________________________________________ 记作____________________ 直线与平面垂直的判定定理：能力提升如图正方体ABGD J ABCD中，求证: BD1平面A]C 1D 三、巩固应用图形表示: 符号语言：___________________________________________________________ 2、思考：上述定理体现的数学思想是什么? 1. 直线I和平面内两条直线都垂直，则I与平面的位置关系是（）A .垂直B .平行C .相交但不垂直D .都有可能2. 已知直线a , b和平面，下列错误的是（）3、什么叫斜线？什么叫斜线在平面内的射影？直线与平面所成的角； _____________________________________________________________________________________特殊的，直线与平面垂直时所成的角为90°。

直线与平面平行或在面内时所成的角是___________________ 直线与平面所成的角的范围是： ____________________________________、理解应用aA a bbCaba // 或ab3. a , b是异面直线，那么经过A. 只有- 个平面与a平行C. 只有- 个平面与a垂直D. a // 且b 则a // bb的所有平面（）B .有无数个平面与a平行D .有无数个平面与a垂直B. a // b 且a 则b例1 ：已知a // b, a ，求证：b4•两条直线和一个平面所成的角相等，则这两条直线的位置关系是5.若平面 //平面，直线a ，则a与的位置关系是 ________________________________________思考：上题改用文字叙述？ __________________________________________________________________________研究：（1）课本P66页探究（2）课本P67 练习1 , 26、直三棱柱ABC AB1C1的所有棱长均为a , D是棱B1C1的中点，求AD与底面ABC所成角的正切值例2：正方体A1B1C1D1 ABCD中，求直线AB和平面A1B1CD所成的角C1A Bd。

青岛高二数学知识点总结在高中数学学习中，数学知识点的掌握是非常重要的。

本文将为大家总结青岛高二数学的知识点，帮助同学们更好地复习和回顾。

一、函数与方程1. 函数的概念与性质：定义域、值域、奇偶性、单调性等。

2. 一次函数：函数图像、斜率、截距等。

3. 二次函数：函数图像、顶点、轴、对称性等。

4. 指数与对数函数：性质、图像与性质的关系等。

5. 三角函数：正弦、余弦、正切等的定义与性质。

二、立体几何1. 空间几何体的表示与性质：点、直线、平面、体、棱、面等。

2. 平行线与平面：平行线与平面的性质、平面间夹角等。

3. 空间直角坐标系：空间直角坐标系的建立、证明等。

4. 球面与球：球面的性质、切球等。

三、概率与统计1. 随机事件与概率：样本空间、事件、概率的计算等。

2. 事件间的关系与运算：和事件、积事件、对立事件等。

3. 随机变量与概率分布：离散型随机变量、连续型随机变量等。

4. 统计与抽样调查：抽样方法、样本均值与总体均值的关系等。

四、数列与数学归纳法1. 数列的概念：等差数列、等比数列等。

2. 等差数列与等比数列的性质：通项公式、前n项和等。

3. 数学归纳法：基本思想、证明方式等。

五、平面几何1. 图形的基本性质：点、线段、角、三角形等。

2. 图形的相似性与全等性：相似三角形、全等三角形等。

3. 三角形的性质与关系：三角形的内角和、外角和等。

六、解析几何1. 坐标系与直线：直线的方程、直线的位置关系、距离公式等。

2. 圆与圆的方程：圆的性质、圆的方程、直线与圆的关系等。

3. 二次曲线：抛物线、椭圆、双曲线等的性质与方程。

七、导数与微分1. 导数的概念与计算：导数的定义、导数的运算性质等。

2. 函数的极值与最值：极值的定义、最值的判定等。

3. 微分与微分近似：微分的定义、微分近似的应用等。

以上是青岛高二数学的知识点总结，希望能对同学们的数学学习有所帮助。

同学们在复习过程中，可以结合教材和练习题，有针对性地复习不同的知识点，加深对数学的理解和应用能力。

山东省青岛第九中学2023-2024学年高二下学期期中阶段检测数学试题一、单选题 1．已知1()2P B A =，2()5P A =，则()P AB 等于（ ） A ．15B ．45C ．910 D ．542．某4位同学排成一排准备照相时，又来了2位同学要加入，如果保持原来4位同学的相对顺序不变，则不同的加入方法种数为（ ） A ．10B ．20C ．24D ．303．中国南北朝时期的著作《孙子算经》中，对同余除法有较深的研究.设,,(0)a b m m >为整数，若a 和b 被m 除得的余数相同，则称a 和b 对模m 同余，记为()mod a b m ≡.若()1222020202020C 2C 2C 2,mod9a a b =⋅+⋅++⋅≡L ，则b 的值可以是（ ）A ．2018B ．2020C ．2022D ．20244．已知甲、乙两人进行五局球赛，甲每局获胜的概率是35，且各局的胜负相互独立，已知 甲胜一局的奖金为10元，设甲所获得的资金总额为X 元，则甲所获得奖金总额的方差()D X =（ ） A ．120B ．240C ．360D ．4805．已知函数()ln f x x ax =-在区间[]1,3上单调递减，则实数a 的取值范围为（ ） A ．1a ≥ B ．1a >C ．13a ≥D ．13a >6．三个数22lne e a =，b =ln33c =的大小顺序为（ ） A ．b c a << B ．b a c << C ．c a b << D ．a b c <<7．某校为推广篮球运动，成立了篮球社团，社团中的甲、乙、丙三名成员进行传球训练，从甲开始随机地传球给其他两人中的任意一人，接球者再随机地将球传给其他两人中的任意一人，如此不停地传下去，且假定每次传球都能被接到．记开始传球的人为第1次触球者，第n 次触球者是甲的概率为n P ，则6P ＝（ ）A ．316 B ．14C ．516D ．388．已知定义在R 上的函数()f x 的导数为()f x '，()1e f =，且对任意的x 满足()()e x f x f x <'-，则不等式()e x f x x >的解集是（ ）A ．(),1-∞B ．(),0∞-C ．()0,∞+D ．()1,+∞二、多选题9．下列说法正确的是（ ）A ．两位男生和两位女生随机排成一列，则两位女生不相邻的概率是12B ．已知随机变量~(,)X B n p ，若()30,()10E X D X ==，则13p =C ．已知23A C n n =，则8n =D ．从一批含有10件正品、4件次品的产品中任取3件，则取得2件次品的概率为459110．已知函数()2()e xf x x ax =+，则下列说法正确的是（ ）A ．当2a =-时，()f x 在[1,1]-上单调递减B ．当2a =-时，函数()f x 没有最值C ．当2a =-时，过原点且与()f x 相切的直线有两条D ．对任意a ∈R ，函数()f x 恒有两个极值点11．已知函数()21e 2x f x x x =--，()f x '为()f x 的导函数，则下列说法正确的是（ ）A ．函数()()g x f x '=的极小值为1B ．函数()f x 在R 上单调递增C ．()2,1x ∃∈--，使得()0012f x x '=-D ．若()210,4x f x x a ∀<<-+恒成立，则整数a 的最小值为2三、填空题12．设随机变量ξ服从正态分布(21)N ,，若(3)(12)P a P a ξξ<-=>-，则实数=a ． 13．核桃（又称胡桃、羌桃）、扁桃、腰果、榛子并称为世界著名的“四大干果”．它的种植面积很广，但因地域不一样，种植出来的核桃品质也有所不同：现已知甲、乙两地盛产核桃，甲地种植的核桃空壳率为2%（空壳率指坚果，谷物等的结实性指标，因花未受精，壳中完全无内容，称为空壳），乙地种植的核桃空壳率为4%，将两地种植出来的核桃混放在一起，已知甲地和乙地核桃数分别占总数的60%，40%，从中任取一个核桃，则该核桃是空壳的概率是．14．若对任意的12,(,)x x m ∞∈+，且12211221ln ln ,2x x x x x x x x -<<-，则实数m 的取值范围是.四、解答题15．已知二项式(0na <且a 为常数)的展开式中第7项是常数.(1)求n 的值；(2)若该二项式展开式中各项系数之和为1024，求展开式中52x 的系数. 16．袋中有大小形状相同的5个球，其中3个红色，2个黄色.(1)两人依次不放回各摸一个球，求第一个人摸出红球，且第二个人摸出1个黄球的概率； (2)甲从中随机且不放回地摸球，每次摸1个，当两种颜色的球都被摸到时即停止摸球，记随机变量X 为此时已摸球的次数，求：①()2P X =的值；②随机变量X 的概率分布和数学期望.17．设函数()()e R xf x x a a =-∈．(1)讨论函数()f x 的单调性；(2)若()f x ax ≤在[0,)x ∈+∞时恒成立，求a 的取值范围．18．某商店随机抽取了当天100名客户的消费金额，并分组如下：[)0,200，[)200,400，[)400,600，…，[]1000,1200（单位：元），得到如图所示的频率分布直方图.(1)若该店当天总共有1350名客户进店消费，试估计其中有多少客户的消费额不少于800元；(2)若利用分层随机抽样的方法从消费不少于800元的客户中共抽取6人，再从这6人中随机抽取2人做进一步调查，则抽到的2人中至少有1人的消费金额不少于1000元的概率是多少；(3)为吸引顾客消费，该商店考虑两种促销方案.方案一：消费金额每满300元可立减50元，并可叠加使用；方案二：消费金额每满1000元即可抽奖三次，每次中奖的概率均为13，且每次抽奖互不影响.中奖1次当天消费金额可打9折，中奖2次当天消费金额可打6折，中奖3次当天消费金额可打3折.若两种方案只能选择其中一种，小王准备购买的商品又恰好标价1000元，请帮助他选择合适的促销方案并说明理由. 19．已知常数m ∈R ，设()ln m f x x x=+， (1)若1m =，求函数()y f x =的最小值；(2)是否存在1230x x x <<<，且1x ，2x ，3x 依次成等比数列，使得()1f x 、()2f x 、()3f x 依次成等差数列？请说明理由．(3)求证：“0m ≤”是“对任意()12,0,x x ∈+∞，12x x <，都有()()()()1212122f x f x f x f x x x ''+->-”的充要条件．。