当前位置：文档之家 › 多组资料均数的比较

多组资料均数的比较

  • 格式：ppt
  • 大小：724.05 KB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

方差分析F检验

方差分析F检验

F值
总变异 310.0
31
组间 163.5
3
54.5 10.48
组内 146.5
28
5.2
.
36
5 确定P值
依椐组间自由度 υ1=3
组内自由度
υ2=28
查F界值表
0.01水平 F(3,28)=4.59 本例F=10.48> F(0.01) 故P<0.01
判断结果 拒绝H0, 接受H1 结论:不同季节湖水氯化物含量的均数差别 有高度显著性(P<0.01)
ni
C (各组样本含量相等)
本例各组样本含量相等.故
109 .86 SS组间= (17.91 )2(15.39 )2(13.91 )2(12.39 )2 8
=11130.3-10966.8=163.5
.
33
(4) 求组内变异的离均差平方和(SS组内)
SS组内=SS总-SS组间=310-163.5=146.5 或 SS组内=∑(ni-1)Si2=∑SSi
16.9
20.1
16.7
16.2
21.2
19.6
14.8
159.3 131.9 129.3 592.4 (∑X)
8 19.91
3231.95
8 16.49 2206..27
8 16.16
2114.11
32 18.51
11276.84
(N)
_
( X)
(∑X2) 8
方差分析的统计量为F值(均方比)
F=MS(组间) / MS误差(组内) (单因素方差分析)
.
3
第一节 方差分析的原理、条件及应用
.
4
方差——均方差——离均差平方和/自由度,用MS表示

方差分析

方差分析

二期矽肺 100.67 93.47 74.97 88.06 113.52 101.14 95.10 118.98
三期矽肺 97.58 83.58 103.81 107.10 108.42 82.58 89.01 77.11
方差分析的基本思想
总变异：从例中看出，32个观察值大小参差不 齐，这种个体值与总均数之间的差异称为总变 异。
多个样本均数间的多重比较
多个样本均数间的多重比较：也称为两两 比较，主要用于探索与证实多组均数中， 哪两个总体均数间有差别，哪两个均数间 没有差别。 如果多组均数的比较采用两样本均数比较 的t检验，会加大I型错误。
多个样本均数间的多重比较
LSD-t检验：最小显著差法
容易获得P<0.05，但是假阳性率较高；
完全随机设计资料的方差分析
方差分析结果表 变异来源 总 组间 组内 SS 86.740 45.091 41.649 ν 39 3 36 MS F P <0.05
15.030 12.990 1.157
3.确定P值和作出推断结论：以ν组间=3，ν组内=36， 查F界值表得P<0.05， 按α=0.05水准拒绝H0 ，接受 H1，故可以认为给予不同剂量的三菱莪术液，小鼠瘤 重间差别有统计学意义。
方差分析
主要内容
方差分析的基本思想 完全随机设计、随机区组设计、拉丁方设 计、交叉设计和析因设计资料方差分析的 基本过程
多个样本均数的比较
两个样本均数的比较：
1次t-test，α=0.05；
三个样本均数的比较：
3次t-test，α=1-（1-0.05）3=0.14；
四个样本均数的比较：
6次t-test，α=1-（1-0.05）6=0.26；

多组间比较检验方法

多组间比较检验方法

多组间比较检验方法
首先，方差分析（ANOVA）是用来比较两个以上组别的均值是否
存在显著差异的统计方法。

当方差齐性假设成立时，可以使用单因
素方差分析；当方差齐性假设不成立时，可以使用Welch修正的ANOVA方法。

其次，Kruskal-Wallis检验是一种非参数检验方法，用于比较
两个以上独立组别的中位数是否存在显著差异。

它适用于数据不满
足正态分布或方差齐性的情况。

另外，Friedman检验是用于比较三个以上相关样本的非参数检
验方法，适用于重复测量设计或配对设计的数据。

此外，多重比较方法用于解决多组间比较时产生的问题，如误
差率的调整和多重比较校正。

常见的多重比较方法包括Bonferroni
校正、Tukey-Kramer校正、False Discovery Rate（FDR）校正等。

在选择多组间比较检验方法时，需要考虑数据的分布特征、方
差齐性、样本的独立性以及实验设计等因素。

不同的方法适用于不
同的数据类型和研究设计，选择合适的方法对于得出准确的统计结
论至关重要。

最后，需要注意在进行多组间比较时，应该进行适当的多重比较校正，以控制整体的显著性水平，避免产生误导性的统计结论。

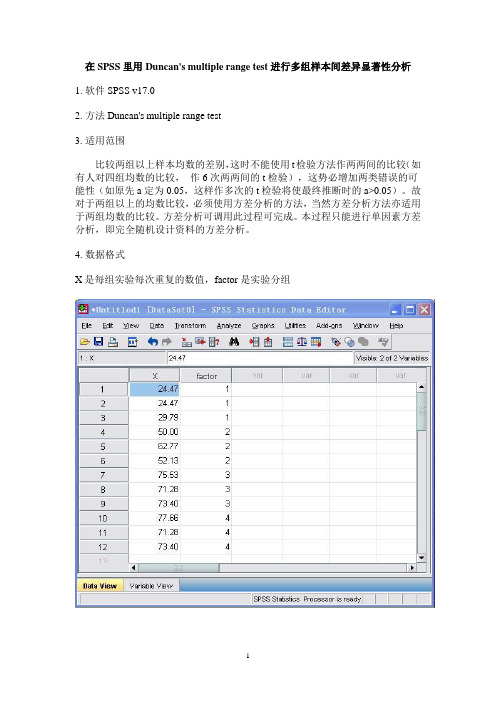
在SPSS里用Duncan法进行多组样本间差异显著性分析

在SPSS里用Duncan法进行多组样本间差异显著性分析

在SPSS里用Duncan's multiple range test进行多组样本间差异显著性分析1. 软件SPSS v17.02. 方法Duncan's multiple range test3. 适用范围比较两组以上样本均数的差别，这时不能使用t检验方法作两两间的比较（如有人对四组均数的比较，作6次两两间的t检验），这势必增加两类错误的可能性（如原先a定为0.05，这样作多次的t检验将使最终推断时的a>0.05）。

故对于两组以上的均数比较，必须使用方差分析的方法，当然方差分析方法亦适用于两组均数的比较。

方差分析可调用此过程可完成。

本过程只能进行单因素方差分析，即完全随机设计资料的方差分析。

4. 数据格式X是每组实验每次重复的数值，factor是实验分组5. 实现方法Analyze->Compare Means->One-Way ANOVA点击PostHoc...选择方法，设置显著水平6. 查看结果看Post Hoc Tests部分的表格按照显著性水平P<0.05分成3列，三者之间有着显著性差异（factor1，factor2，factor3和factor4），factor3和factor4之间差异不显著。

7.在表格中标明差异显著性根据这一结果即可做表格，四组分别以a,b,c,c标明其显著性差异。

小写字母代表是在0.05水平下比较，差异显著；大写字母代表在0.01水平下比较，差异极显著。

上图标注有误，abcd的标注由值的大小决定，a表示最大，因此从上到下应为：cbaa参考资料SPSS FOR WINDOWS简明教程标记字母法：（1）将全部平均数从大到小依次排列。

（2）在最大的平均数上标上字母a；将该平均数与以下各平均数相比，相差不显著的，都标上字母a，直至某一个与之相差显著的平均数则标以字母b(向下过程)，（3）再以该标有b的平均数为标准，与上方各个比它大的平均数比，凡不显著的也一律标以字母b(向上过程)；再以该标有b的最大平均数为标准，与以下各未标记的平均数比，凡不显著的继续标以字母b，直至某一个与之相差显著的平均数则标以字母c。

方差分析

方差分析

第7章方差分析摘要：多组资料均数比较一般采用方差分析的方法，SAS中方差分析的功能非常全面，能实现方差分析功能的过程有ANOV A过程和GLM过程。

对于两个平均数的假设测验，一般采用t测验来完成，对于多个平均数的假设测验，若采用t测验两两进行，不仅非常麻烦，而且容易犯第一类错误。

方差或称均方，即标准差的平方，它是一个表示变异程度的量。

在一项试验或调查中往往存在着许多种影响生物性状变异的因素，这些因素有较重要的，也有较次要的。

方差分析就是将总变异分裂为各个因素的相应变异，作出其数量估计，从而发现各个因素在变异中所占的重要程度；而且除了可控制因素所引起的变异后，其剩余变异又可提供试验误差的准确而无偏的估计，作为统计假设测验的依据。

当试验结果受到多个因素的影响，而且也受到每个因素的各水平的影响时，为从数量上反映各因素以及各因素诸水平对试验结果的影响，可使用方差分析的方法。

SAS系统用于进行方差分析的过程主要有ANOV A过程和GLM过程，对于均衡数据的分析一般采用ANOV A过程，对于非均衡数据的分析一般采用GLM过程。

方差分析和协方差分析在SAS系统中由SAS/STAT模块来完成，其中我们常用的有ANOV A过程和GLM过程。

前者运算速度较快，但功能较为有限；后者运算速度较慢，但功能强大，我们做协方差分析时就要用到GLM过程。

本章将首先介绍方差分析所用数据集的建立技巧，然后重点介绍这两个程序步。

§7.1 方差分析概述一、方差分析的应用场合、基本思想和前提条件1．应用场合当影响因素是定性变量（一般称为分组变量或原因变量），观测结果是定量变量（一般称为结果变量或反应变量），常用的数据处理方法是对均数或均值向量进行假设检验。

若只有一个原因变量，而且其水平数k≤2，一元时常用U检验、t检验、秩和检验，多元时用多元检验（T2检验或wilks’^检验）；若原因变量的水平数k≥3或原因变量的个数≥2，一元时常用下检验，也叫一元方差分析（简写成ANOV A）或非参数检验，多元时用多元方差分析（简写成MANOV A，其中最常用的是Wilks’^检验）。

三组或三组以上服从正态分布且方差齐同的定量资料均数间两两比较时,采用t检验将会

三组或三组以上服从正态分布且方差齐同的定量资料均数间两两比较时,采用t检验将会

三组或三组以上服从正态分布且方差齐同的定量资料均数间两两比较时,
采用t检验将会
t检验是进行定量资料两组或多组的比较时的检验手段，尤其在三组或三组以
上服从正态分布且方差齐同的定量资料均数间两两比较时，更是重要工具。

一般来说，t检验法要求两种不同资料，相应观察值要求服从正态分布，并且要求在数量
相当的前提下方差齐同，并且资料要极为客观，表达能力强，这样做出来的检验结论才具有实时性，具有一定的科学依据。

面对复杂的专业知识时，多少会觉得门槛很高——比如t检验，它是一种统计
方法，是统计学的重要内容，众多的学者和科研人员也正在深入探索和使用t检验。

从经典t检验到现代t检验，它们都被用来解决问题，摆脱空前的统计迷思，正确识别，合理使用t检验，可以更好地表现出科学精神，同时也是现代社会的发展和进步所带来的科学智慧的体现。

t检验技术也因其独特的理论和计算方法，而成为社会研究的重要工具。

它具
有极高的可读性、可操作性和实际可用性，可以得到明确的判断结果，从而较好地支持数据的推导和决策，受到广泛应用。

此外，由于它具有良好的鲁棒性和抗干扰能力，所产生的统计结论也被越来越多的社会研究者所认可。

因此，在定量资料两组或多组的比较时，t检验凭借其良好的数据分析能力，
可以有效辅助社会研究生成准确可信的统计结论，为改变某种现状，实现目标提供可靠参考。

特别是在三组或三组以上的定量资料均数间两两比较中，t检验具有极
其重要的意义，有效改善社会统计学研究的客观性，堪称一绝。

医学统计学测试

医学统计学测试51方差分析的基本思想和要点是:A、组间均方大于组内均方B、组内均方大于组间均方C、不同来源的方差必须相等D、两方差之比服从F分布E、总变异及其自由度可按不同来源分解(正确答案)2方差分析的应用条件之一是方差齐性,它是指:（）A、各比较组相应的样本方差相等B、各比较组相应的总体方差相等(正确答案)C、组内方差=组间方D、总方差=各组方差之和E、总方差=组内方差+组间方差3完全随机设计方差分析中的组间均方反映的是:（）A、随机测量误差大小B、某因素效应大小C、处理因素效应与随机误差综合结果(正确答案)D、全部数据的离散度E、各组方差的平均水平4对于两组资料的比较,方差分析与t检验的关系是:（）A、t检验结果更准确B、方差分析结果更准确C、t检验对数据的要求更为严格D、近似等价E、完全等价(正确答案)5多组均数比较的方差分析,如果pA、两均数的t检验B、区组方差分析C、方差齐性检验D、posthoc检验(正确答案)E、确定单独效应6完全随机设计的多样本均数的比较,经方差分析,若P〈0.05,则结论为:（）A、各样本均数全相等B、各样本均数全不相等C、至少有两个样本均数不等D、至少有两个总体均数不等(正确答案)E、各总体均数全相等7对于多个方差的齐性检验,若P〈a,可认为:（）A、多个样本方差全不相等B、多个总体方差全不相等C、多个样本方差不全相等D、多个总体方差不全相等(正确答案)E、多个总体方差相等8某职业病防治院测定了年龄相近的45名男性用力肺活量,其中石棉肺患者、石棉肺可疑患者和正常人各15名,其用力肺活量分别为(1.79±0.L、(2.31±0.L和(3.08±0.L,拟推断石棉肺患者、石棉肺可疑患者和正常人的用力肺活量是否不同,宜采用的假设检验的方法是:（）A、两组均数比较的t检验B、方差齐性检验C、完全随机设计方差分析(正确答案)D、随机区组方差分析E、析因设计方差分析9某职业病防治院测定了年龄相近的10名男性工前、工中、工后肺活量,其用力肺活量分别为(3.08±0.L、(2.31±0.L和(1.79±0.L,拟推断石工前、工中和工后的用力肺活量是否不同,宜采用的假设检验的方法是:（）A、两组均数比较的t检验B、方差齐性检验C、完全随机设计方差分析D、随机区组方差分析(正确答案)E、析因设计方差分析10完全随机设计资料的多个样本均数的比较,若处理或干预因素无作用或效果,则方差分析的F值理论上应接近:（）A、Fa(v1,v2)B、SS处理/SS误差C、0D、1(正确答案)E、任意值11完全随机设计的方差分析的基本思想和要点是:（E）A、组间均方大于组内均方B、组内均方大于组间均方C、不同来源的方差必须相等D、两方差之比服从E、总变异及其自由度可按不同来源分解为组间和组内两部分(正确答案)12随机区组设计的方差分析的基本思想和要点是:（）A、组间均方大于组内均方B、组内均方大于组间均方C、不同来源的方差必须相等D、两方差之比服从E、总变异及其自由度可按不同来源分解为组间、区组和组内三部分(正确答案) 13完全随机设计的方差分析中,下列式子中正确的是:（）A、SS总=SS组间+SS组内(正确答案)B、MS总=MS组间+MS组内C、SS组间大于SS组内D、MS组间大于MS组内E、v组间小于v组内14随机区组设计的方差分析中,以下对变异间关系表达正确的是:（）A、SS总=SS组间+SS组内B、MS总=MS组间+MS组内C、SS总=SS处理+SS区组+SS误差(正确答案)D、MS总=MS处理+MS区组+MS误差E、SS总=SS处理+SS区组+MS误差15若要研究某主要的干预因素对实验结局的影响,研究分为3个组(该干预因素的三个水平),但同时也知道另一个因素也可能对实验结局造成影响,如果不考虑因素间的交互作用,所采用的实验设计类型最好为:（）A、配对设计B、完全随机化设计C、随机区组设计(正确答案)D、交叉设计E、拉丁方设计16随机区组化设计的方差分析中区组均方反应的是:（）A、随机测量误差大小B、某因素效应大小C、区组因素效应与随机误差综合结果(正确答案)D、全部数据的离散度E、各组方差的平均水平17某医科大学某教研组研究棉布、府绸、的确凉、尼龙4种衣料对棉花吸附十硼氢量(γ)。

统计学第四讲两组资料均数比较2

优点：配对设计减少了个体差异。
特点：资料成对，每对数据不可拆分。
计算出各对子差值d 的均数d 。当比较组间效果相同时， d 的总体均数 d ＝0，故可将配对设计资料的假设检验视为样 本均数d 与总体均数 d =0 的比较，所用方法称为配对 t 检验 （paired t-test）方法。 t | d d | | d | , n 1
或50）时，可采用u检验；但只是近似方法。 优点：简单，u界值与自由度无关， u0.05＝1.96， u0.01＝2.58
u X1 X2 S
X1 X 2
X1 X2 S12 S22 n1 n2
X1 X2
S 2S 2
X1
X2
第四军医大学卫生统计学教研室 2020年3月28日
五、正态性检验与两方差齐性检验
义
第四军医大学卫生统计学教研室 2020年3月28日
假设检验的步骤
1、建立假设与确定检验水准（α）
H0: μ1＝μ2 无效假设（null hypothesis） H1: μ1≠μ2 备择假设（alternative hypothesis）
检验水准（level of a test）：α=0.05(双侧)
今 F 1.484 F0.05 / 2,6,6 ，P>0.05 ，按α=0.05 水准，不拒绝 H0，两组总体
方差的差别无统计学意义，尚不能认为两组总体方差不等。
若两总体方差不等，即
2 1
2 2
时，
1. 近似 t 检验(separate variance estimation t-test) t'检验
n1
2.6314 1.342 / 12 0.475 12 1
t | d | 0.112 0.817, n 1 12 1 11

在统计分析中多组计量资料比较为什么不能用t检验

一
１个 实验 组 与一个 对 比组 均数 差别 的 多重 比较 ） 。 本刊 编辑 部
３３ 染疫羊畜主感染率高于曾报道的畜主感染率 ．
有报 道混有 染疫 羊的羊 群畜 主布鲁 氏菌 的感 染 率 为 ２． ％ Ｉ ，据 丹东 市 ２０ ５２ ３ ］ ０４年 布 病疫 情 畜 间应 急 监 测 ，混 有 染 疫 羊 的 羊 群 畜 主 感 染 率 为 ４ ．７ ，可 能是 由于 患家 在 接 触羊 绒 和羊 流 产 物 １６ ％ 时 防护较差 ，圈舍 无消 毒措施 等情况 有关 。
不犯 Ｉ 类错 误 的概率 为 （ — ． ５ ，６次均 不犯 Ｉ类错 误 的概 率 为 （ — ． ５ 。 １ ００ ） １ ０ ０ ） ，这 时 ，总 的检验 水 准变 为 １ （ 一 ． ５ 。 ０ ２ ，比 ０ Ｏ 一 １ Ｏ０ ）＝ ．６ ． ５大 多 了。 因此 ， 多组均 数 间 的 比较 不能 直
３ ４ 疫 情 出现 可能原 因及 建议 ．
加强部门合作 、同步监测和信息互通等工作 ，共同 做好 布病 防控 工作 。
参 考文献 ：
［ ］ 中华人民共 和国卫生部 ．中国布鲁 氏菌病 防治现状 ［ ］ １ Ｊ
北 京 ：人 民卫 生 出版 社 ，２ ０ ０９：１． ０
［ ］ 尚德秋 ．布鲁氏菌病再 度肆虐及Βιβλιοθήκη 原 因 ［ ］．中国地方病 ２ Ｊ
７ ０
辽宁医学院学 报
２１ ０ ０年 ２月 ，３ １ １（ ）
屠宰、销售等工作人员。提示今后丹东市布病防控
工作要 突 出重 点 ，至少 要 于 ６～ ７月 在凤 城 市 做好 从 事绒 山羊饲 养 、屠 宰 、销售等 工作 的青壮 年人群 防控工作 。
经费投 入不 足等 因素造 成 了布 氏杆 菌的 引入并 在地 方流行 开来 ，而在 高危人 群 中防治 宣传不 到位 ，群 众 自我 防护 意识差 等 因素 导致 了人 间布病疫 情 的发 生 。所 以 ，今后 要 进 一 步完 善 联 防联 控 工作 机 制 ，

第7章-多组定量资料的比较思考与练习参考答案

第7章 多组定量资料的比较思考与练习参考答案一、最佳选择题1. 完全随机设计资料的方差分析中，必然有（ C ）。

A. 组间SS >组内SSB. 组内组间总MS MS MS +=C. 总ss=组间SS +组内SSD. 组内组间MS MS >E. 组间组内νν> 2. 定量资料两样本均数的比较，可采用（ D ）。

A. t 检验B.F 检验C. Bonferroni 检验D. t 检验与F 检验均可E. LSD 检验3. 当组数等于2时，对于同一资料，方差分析结果与t 检验结果相比，（ C ）。

A. t 检验结果更为准确B. 方差分析结果更为准确C. 完全等价且F t =D. 完全等价且t F =E. 两者结果可能出现矛盾4. 若单因素方差分析结果为),(01.021ννF F >,则统计推断是（ D ）。

A. 各样本均数都不相等B. 各样本均数不全相等C. 各总体均数都不相等D. 各总体均数不全相等E. 各总体均数全相等 5. 完全随机设计资料的方差分析中，组间均方表示（ C ）。

A. 抽样误差的大小B. 处理效应的大小C. 处理效应和抽样误差综合结果D. N 个数据的离散程度E. 随机因素的效应大小 6. 多样本定量资料比较，当分布类型不清时应选择（ D ）。

A. 方差分析B. t 检验C. Z 检验D. Kruskal-Wallis 检验E. Wilcoxon 检验7. 多组样本比较的Kruskal-Wallis 检验中，当相同秩次较多时，如果用H 值而不用校正后的c H 值，则会（ C ）。

A ． 提高检验的灵敏度B ．把一些无差别的总体推断成有差别 C. 把一些有差别的总体推断成无差别 D ．Ⅰ、Ⅱ类错误概率不变E. 以上说法均不对二、思考题1. 方差分析的基本思想和应用条件是什么？答：方差分析的基本思想是，对于不同设计的方差分析，其思想都一样，即均将处理间平均变异与误差平均变异比较。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

同，但测量值仍各不相同，
这种变异称为组内变异。
SS组内仅仅反映了随机误差
mi
的影响。也称SS误差
k ni
k
SS组内
( X ij X i )2 (ni 1)Si2
i1 j1
i 1
组间＝N k
医学院预防医学教研室 2019年12月4日
三种“变异”之间的关系
SS总 = SS组间 + SS组内 ，
ni
X 1 X 1 j n1 j 1
ni
X 2 X 2 j n2 j 1
ni
X 3 X 3 j n3 j 1
k ni
X X ij N i1 j1
Q1－T12/n1
Q2－T22/n2
Q3－T32/n3
ni
T1 X 1 j j 1
ni
T2 X 2 j j 1
2
(

1
F

2
1 2
)2
F分布表示：
F （v1，v２）
式中 () 为伽玛函数； F 组间均方 组内均方＝MS1 MS2 ， 是两个均方的比值；1 、 2 分别为 F 值的分子与分母的自由度， 这是 F 分布的两个参数，由这两个自由度可决定 F 分布的图
形形状，因此 F 分布可用 F (1, 2 ) 表示。以 F 为横轴， f (F) 为纵轴可绘制 F 分布的图形。
合计
3.49（X31）
3.67（X32） 3.53（X33） 3.41（X34）
i为组的编
号：1，2，3
33..5675（（XX335）6）j为组内为个体编
3.37（X37） 号：1，2，…，11
3.21（X38）
3.33（X39）
3.49（X310）
3.32（X311）
3.41（X312）
n3
N＝n1 + n2 + n3
Commonly referred to as: Sum of Squares Within, or Sum of Squares Error, or Within Groups Variation
医学院预防医学教研室 2019年12月4日
均方(mean square，MS)
变异程度除与离均差平方和的大小有关外， 还与其自由度有关，由于各部分自由度不相等， 因此各部分离均差平方和不能直接比较，须将 各部分离均差平方和除以相应自由度，其比值 称为均方差，简称均方(mean square，MS)。组 间均方和组内均方的计算公式为:
且 ν总 =ν组间 +ν组内
组内变异 SS ： 组内
随机误差
组间变异 SS 组间：处理因素 + 随机误差
医学院预防医学教研室 2019年12月4日
One-Factor ANOVA Partitions of Total Variation
Total Variation SST
= Variation Due to Treatment SSB
医学院预防医学教研室 2019年12月4日
一、方差分析的基本思想及应用条件
将所研究的对象分为多个处理组,施加不同 的干预，施加的干预称为处理因素（factor）， 处理因素至少有两个水平(level)。用这类资料 的样本信息来推断各处理组间多个总体均数是否 存在差别，常采用的统计分析方法为方差分析 (analysis of variance, ANOVA)。
： （X111）
6.26（X21） 4.36（X22） 5.24（X23） 4.67（X24） 4.55（X25） ： （X26） ： （X27） ： （X28） ： （X29） ： （X210）
： （X211）
5.78（X31）
655...648846（（（XXX333234）））i号为：组1的，编2，3 5：.67（（XX3356））j为组内为个体编
对于不同设计的方差分析，其思想都一样，即均将 处理间平均变异与误差平均变异比较。不同之处在于变 异分解的项目因设计不同而异。
医学院预防医学教研室 2019年12月4日
方差分析的应用条件
各样本是相互独立的随机样本； 各样本来自正态总体； 各处理组总体方差相等，即方差齐性或齐
同（homogeneity of variance）。
由英国统计学家R.A.Fisher首创，为纪念
Fisher，以F命名，故方差分析又称F检验 （F
test）。
医学院预防医学教研室 2019年12月4日
n i
Xi
Si
ni
Ti X ij j 1
表 6-2 三组…………………………（L）
正常组（对照）
3.25（X11） 3.37（X12） 3.34（X13） 3.39（X14） 3.21（X15） 3.69（X16） 3.33（X17） 3.57（X18） 3.31（X19） 3.65（X110）
… 32 33 24.4 29.7 8.4 CCA
医学院预防医学教研室 2019年12月4日
表 6-2 三组…………………………………（ L ）
对照组
药物组Ⅰ
药物组Ⅱ
合计
3.25（X11） 3.37（X12） 3.34（X13） 3.39（X14） 3.21（X15） : （X16） ： （X17） ： （X18） ： （X19） ： （X110）

X ij
i1 j1
N
k Ti2 n i1 i
X2 N
Ti2 ni C
其中C X 2 N ; 组间＝k 1
医学院预防医学教研室 2019年12月4日
3. 组内变异（ SS组内）
在同一处理组内，虽然
每个受试对象接受的处理相
0.05 。
（二） 计算 F 值 （三） 查 F 值表（附表 4），确定 P 值，下结论
H0: m1 = m2 = m3 = ... = mk
H1: not all the mi are equal
m1 m2 m3
+
Commonly referred to as:
Sum of Squares Among, or
Sum of Squares Between, or
Sum of Squares Model, or
Among Groups Variation
Variation Due to Random Sampling SSW
41.45
125.11
ni
Q i
X
2 ij
137.9887
154.4315 143.3859
435.8061
j 1
医学院预防医学教研室 2019年12月4日
方差分析的步骤
（一） 建立假设并确定检验水准
H 0 ： m1 m 2 m3 （k不个同总时期 体切均痂数对 全ATP相含等量无影响)； H1 ： m1, m2 , m3 不k全个相总等（体不同 均时数期切不痂等对 或ATP不含量全有相影响等)；
7.77 5.57 4.68
医学院预防医学教研室
2.76 4.18
2.60 3.85
2.49 3.63
2019年12月4日
方差分析的基本思想
首先将总变异分解为组间变异和误差（组内）变异；
然后比较两者的均方，即计算F 值；
若F值大于某个临界值，表示处理组间的效应不同， 若F值接近甚至小于某个临界值，表示处理组间效应 相同(差异仅仅由随机原因所致)。
分母自由度
分子的自由度，υ 1
υ2
1
2
3
4
5
6
161 200 216 225 230 234 1
4052 4999 5403 5625 5764 5859
18.51 19.00 19.16 19.25 19.30 19.33 2
98.49 99.00 99.17 99.25 99.30 99.33
4.24 3.39 2.99 25
随机分组方法： 1. 编号,确定分组方案（如较少11个随机数为A,中间 11个数为B，较大11个随机数为C） 2. 产生随机数字（统计书，或电脑），排序 3. 按方案分组
编号 随机数 分组
12 12.1 3.9 BA
34567 18.3 27.1 26.7 28.8 1.4 ACCCA
8 9 10 12.8 26.0 5.0 B CA
方差分析
———多组资料均数的比较
Dr. 朱彩华 制作 临床医学《医学统计学》
多组资料均数的比较
完全随机设计资料的方差分析 （单因素）
随机区组设计资料的方差分析 （双因素）
析因设计资料的方差分析 （多因素）
医学院预防医学教研室 2019年12月4日
多组资料均数的比较
一、方差分析的基本思想及应用条件 二、完全随机设计资料的方差分析 三、均数间的多重比较
： （X37）号：1，2，…，11
： （X38） ： （X39） ： （X310）
： （X311）
n i
n1=12
n2=12
n3=12
N ＝36
Xi
3.3875
3.5842
3.4542
3.4753
S2 i
0.0261
0.0251
0.0192
0.0290
ni
Ti X ij j 1
40.65
43.01
始数据 与该组均数 X i 的差异（以SS组内表示）
医学院预防医学of squares of deviations from mean，SS)表示变 异的大小
2019年12月4日
1. 总变异（ SS总）