第6章线面积分

一、曲线积分、曲面积分的计算公式1. 对弧长的曲线积分(,)Lf x y ds ⎰的计算公式:(,)Lf x y ds ⎰中，L 为一段光滑的平面曲线，其参数方程为(),t (),x x t y y t αβ=⎧≤≤⎨=⎩ (,)f x y 为定义在曲线L 上的一连续函数.为熟练掌握计算公式，关键是把握以下两点：1)积分变量,x y 在曲线L 上，故,x y 满足曲线L 的方程；2)ds 是曲线L的弧长的微分，故ds =. 所以有如下的计算公式:(,)[(),(Lf x y ds f x t y t βα=⎰⎰.对L 是空间曲线段的情况，有类似的公式. 设L 的方程为 (),(), t (),x x t y y t z z t αβ=⎧⎪=≤≤⎨⎪=⎩(,,)f x y z 在L 上连续，则对弧长的曲线积分(,,)[(),(),(Lf x y z ds f x t y t z t βα=⎰⎰.弧微元 dt t z t y t x ds )(')(')('222++=2. 对坐标的曲线积分(,)(,)ABL P x y dx Q x y dy +⎰在(,)(,)ABL P x y dx Q x y dy +⎰中，AB L 是以A 为起点，以B 为终点，参数方程为 ()()x x t y y t =⎧⎨=⎩的平面曲线，A 点的坐标为((),())x y αα，B 点的坐标为((),())x y ββ.物理意义：变力F沿曲线L 所做的功⎰⎰+=∙=LLQdy Pdx r d F W其中 }.,{;}),(,),({dy dx r d y x Q y x P F ==为熟练掌握该积分的计算公式，关键是把握以下两点：1) 积分变量（,x y ）在AB L 上，故满足曲线方程(),()x x t y y t ==； 2) (),()dx x t dt dy y t dt ''==. 对坐标的曲线积分的计算公式为(,)(,){[(),()]()[(),()]()}ABL P x y dx Q x y dy P x t y t x t Q x t y t y t dt βα''+=+⎰⎰.,αβ分别对应于,A B 点的参数t 的值，可能,αβ<也可能αβ>.类似地，对于空间曲线AB L ，也有类似的计算公式.设AB L 是以A 为起点，以B 为终点，参数方程为 ()()()x x t y y t z z t =⎧⎪=⎨⎪=⎩的空间曲线，A 点的坐标为((),(),())x y z ααα，B 点的坐标为((),(),())x y z βββ，(,,),(,,),(,,)P x y z Q x y z R x y z 在曲线AB L 上连续，则(,,)(,,)(,,)ABL P x y z dx Q x y z dy z x y z dz ++⎰{[(),(),()]()[(),(),()]()[(),(),()]()}P x t y t z t x t Q x t y t z t y t R x t y t z t z t dt βα'''=++⎰.两类曲线积分之间的关系。

一.第一类线面积分的简化充分利用积分曲线与曲面的方程与对称性.例.求(22LI x x y ds ⎡⎤=++⎣⎦⎰ ,其中()22:11L x y +-=.解.(((22222LLLI y ds yds ds π⎤=+=+=+=+⎦⎰⎰⎰. 例.求()I xy z ds Γ=+⎰ ,其中2221:0x y z x y z ⎧++=Γ⎨++=⎩. 解.()()()1233I xyds x y ds xy yz zx ds x y z ds ΓΓΓΓ=-+=++-++=⎰⎰⎰⎰ ()()22221110663x y z x y z ds ds πΓΓ⎡⎤++-++-=-=-⎣⎦⎰⎰ . 注.求()23I x y z ds Γ=++⎰ ,其中2221:0x y z x y ⎧++=Γ⎨+=⎩. 解.()()32333002I x y z ds xds zds x y ds ΓΓΓΓ=++=+=++=⎰⎰⎰⎰ . 例.求()2I x dS ∑=⎰⎰ ,其中222:2x y z y ∑++=.解.()()()222222222342222I x y z dS x y dS x y z dS ∑∑∑=++=+=++=⎰⎰⎰⎰⎰⎰()441416ydS y dS dS π∑∑∑=-+=⎰⎰⎰⎰⎰⎰ .二.第二类线面积分的估值例.设()33cos :02sin x a t L t y a t π⎧=≤≤⎨=⎩,逆时针方向,()()222L ydx xdy F a x xy y -=++⎰ , 证明:()lim 0a aF a →+∞=. 解.设()222yP xxy y=++,()222xQ xxy y-=++,则()LF a Pdx Qdy =+=⎰(),max 6n LLLP Q e ds ds a ⋅≤≤=⋅⎰⎰⎰,而22222x y x xy y +++≥()3322222432a x xy y x y =≤≤+++,故 ()2192F a a ≤,因此()lim 0a aF a →+∞=.例.设∑为圆柱体()()()2200413x x y y z -+-≤≤≤的外表面,证明:()()22cos sin 2x y dydz xy dzdx dxdy ∑+++≤⎰⎰ . 证.()n n A dS A e dS A e dS A dS dS ∑∑∑∑∑⋅=⋅≤⋅≤≤⎰⎰⎰⎰⎰⎰⎰⎰,证毕.注.第二类线面积分的估值除了转化为第一类线面积分,也可以 用格林公式和高斯公式转化为重积分.例.设22:0L x y x y +++=,逆时针,证明:22cos sin Lx y dy y x dx -≤⎰证.左式()()2222cos sin cos sin 2DDy x d x x d πσσ=+=+≤⎰⎰⎰⎰,证毕.例.设22:1L x y +=,逆时针,证明:sin sin 222545y x Lxe dy ye dx x y π--≥+⎰. 证.左式sin sin sin sin sin sin 222254545y x y x y xL D D xe ye e e e e dy dx d y x y x σ---⎛⎫+=-=+≥= ⎪-+-+⎝⎭⎰⎰⎰⎰⎰ ()sin sin 122555x xD D e e d d σσπ-+≥=⎰⎰⎰⎰,即得,证毕. 三.第二类线积分的计算 例.求224Lxdy ydxI x y-=+⎰,其中L 从()1,0A -沿y =到()1,0B ,然后 再沿直线到()1,2D -的有向曲线.解一. cos :sin x tAB y t=⎧⎨=⎩,:0t π-→,:1BD y x =-+,:11x →-,故12221374cos sin 521288dt dx I t t x x ππππ---=+=+=+-+⎰⎰; 解二.由于Q Px y ∂∂=∂∂,故取()1,1C --,()1,1E -,()1,2F ,则 ACCEEBBFFDI =++++⎰⎰⎰⎰⎰;解三.除原点,Q Px y ∂∂=∂∂,取222:4C x y r +=,逆时针,则L DA DAI +=-=⎰⎰ 222222241172488CDAx y r xdy ydx dy dxdy r r y πππ+≤---=-=-=+⎰⎰⎰⎰⎰. 注.若在区域D 内Q Px y ∂∂=∂∂,则(1)当D 单连通时,0CPdx Qdy +=⎰ ; (2)当D 内有洞时,对所有绕洞的闭曲线C ,CPdx Qdy +=⎰ 常数.例.求()()()()22222222222222L y y x xI dx dy x y x y x y x y ⎡⎤⎡⎤-+=++-⎢⎥⎢⎥-+++-+++⎢⎥⎢⎥⎣⎦⎣⎦⎰ , 其中22:9L x y +=,取逆时针方向.解.取()2221:2L x y r -+=,()2222:2L x y r ++=,均为逆时针方向,则12L L I =+⎰⎰ ,而()()112222222222222r L L B y y x x dx dy d r r r x y x y σπ⎡⎤⎡⎤-+-=++-==-⎢⎥⎢++++⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰⎰⎰ , 类似地,22L π=-⎰ ,故224I πππ=--=-.例.求x y z dx y z x dy z x y dz I +-++-++-=,其中的Γ为曲线22211x y z x y z ⎧++=⎨++=⎩上逆时针从()1,0,0A 到()0,0,1B 的一段弧.解一.2221:1x y z x y z ⎧++=Γ⎨++=⎩在xOy 上的投影为22:0x xy y x y 'Γ++--=,22223x y x xy y ξηξηξη=-⎧⎨=+⎩++=+,故2222032x xy y x y ξηξ++--=⇒+-=2211333ξη⎛⎫-+= ⎪⎝⎭,令11cos 3311cos 1133cos 33121cos 33x t t t y t t tz x y tξη⎧=+-⎪⎧⎪=+⎪⎪⎪⇒=++⎨⎨⎪⎪=⎪⎪⎩=--=-⎪⎩,又:013z t ππ→⇒=-→,故3I dt ππ==⎰. 解二.()()()12121212BABAI z dx x dy y dz I I ΓΓ+=-+-+-=-=-⎰⎰⎰,其中()11,1,1rot 12,12,12121212n ijkI z x y e dS x y z z x y∑∑∂∂∂=---⋅==∂∂∂---⎰⎰⎰⎰()11,1,12122,2,23332I dS ππ∑∑⎡⎤⎛⎫=---==--⎥ ⎪ ⎪⎥⎝⎭⎦⎰⎰, ()()()112001211221I x dx d x x dx =--+-=-=-⎡⎤⎣⎦⎰⎰,故I =.注.∑是边长为的等边三角形的外接圆减去一个小圆缺. 解三.代入1z x y =--,则()()221I x y dx x y dy 'Γ=+---=⎰()()1042216216196D OAOA x dx d x dx σπ'Γ+⎛⎫--=---=-+= ⎪ ⎪⎝⎭⎰⎰⎰⎰⎰ . 注.求()()()22222223I y z dx z x dy x y dz Γ=-+-+-⎰,其中1:2x y x y z ⎧+=Γ⎨++=⎩,从z 轴正向看为逆时针方向.解.代入2z x y =--,则()()2222223242I x y z dx x y z dy 'Γ=-+-+-++=⎰()12221224xyxyD D x y d d σσ--+=-=-⎰⎰⎰⎰.例.求()22222ydx xdy z x y dzI x y Γ--+=+⎰,其中22221:1x y a b x y z ⎧+=⎪Γ⎨⎪++=⎩,从z 轴正向 看逆时针. 解.2222rot ,,20y xz x y x y ⎛⎫-=⎪++⎝⎭,但是Γ张成的曲面均与z 轴有交点, 故不能直接用斯托克斯公式,注意到对所有逆时针围绕z 轴的1Γ,Γ与1-Γ均张成一个围绕z 轴的曲面,故()111I Γ+-Γ-ΓΓ=-=⎰⎰⎰ ,于是取2211:0x y z ⎧+=Γ⎨=⎩,则122DI ydx xdy d σπΓ=-=-=-⎰⎰⎰ . 四.第二类面积分的计算注.若12∑=∑+∑关于xOy 面对称,1∑与2∑在xOy 面上的投影相反, 则当()(),,,,R x y z R x y z -=时,(),,0R x y z dxdy ∑=⎰⎰;当()(),,,,R x y z R x y z -=-时,()()1,,2,,R x y z dxdy R x y z dxdy ∑∑=⎰⎰⎰⎰.例.求()()()I y z dydz z x dzdx x y dxdy ∑=-+-+-⎰⎰,其中∑为半球面z =222x y x +=截下部分的上侧.解.由于∑关于xOz 面对称,故()()I y z dydz x y dxdy ∑=-+-⎰⎰,又22222424220x x y x zz x x y z x z y zz z +=⎧-++=⇒⇒=⎨+=⎩,y yz z -=,故 ()()()22,0,,,1x y x I y z x y dxdy y z x y dxdy z z z ∑∑---⎛⎫⎡⎤=--⋅--=-+-= ⎪⎢⎥⎝⎭⎣⎦⎰⎰⎰⎰(()22222xy D x y x y x y d d σσπ+≤⎡⎤+-=⋅=⎢⎥⎢⎥⎣⎦⎰⎰⎰⎰.例.求2222cos cos cos dydz dzdx dxdyI x x y z z∑=+-⎰⎰,其中2222:x y z R ∑++=外侧. 解.()222,,211,,cos cos cos x y z I dS x x y z z R ∑⎛⎫=-⋅=⎪⎝⎭⎰⎰ 2222221211211cos cos cos cos cos cos y dSdS dS R x y z R x z R z∑∑∑⎛⎫⎛⎫+-=-== ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰⎰⎰22224tan x y R R π+≤=⎰⎰.例.求()32222xdydz ydzdx zdxdyI xy z∑++=++⎰⎰,其中()()()22211:1025167x y z z --∑++=≥ 上侧.解.取1:z ∑=()()22222211:0,12516x y z x y r ⎛⎫--∑=+≥+≤ ⎪ ⎪⎝⎭,均取下侧,则12121312I xdydz ydzdx zdxdy r π∑+∑+∑∑∑-∑=--=++=⎰⎰⎰⎰⎰⎰⎰⎰ . 注.若()22:212z x y z ∑=+--≤≤外侧,可取()221:24z x y ∑=+≤上侧,()222:11z x y ∑=-+≤下侧,22223:x y z r ∑++=外侧,则 ()121231231=I xdydz ydzdx zdxdy r ∑+∑+∑∑∑∑∑∑=--=++--⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰换曲面,再用高斯公式.。

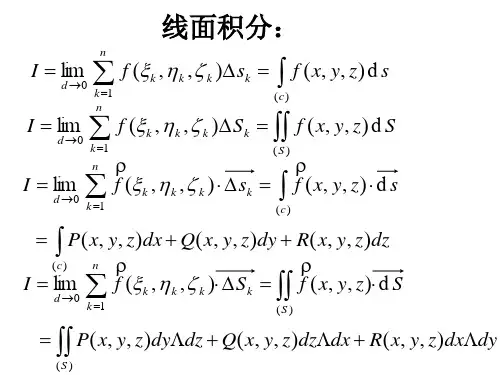
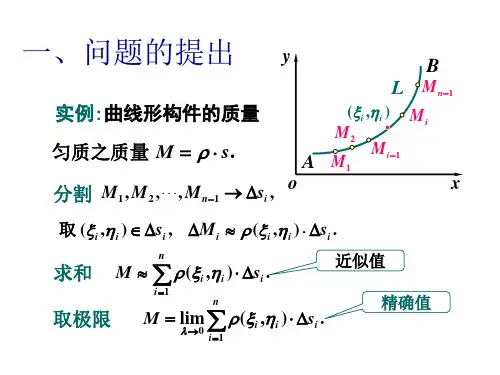
（同学们认真做好笔记，将方法进行补充完整，其中，L 为平面曲线，Γ为空间曲线）（线面积分）计算方法总结：1.第一类曲线积分：.),,(;),(dS z y x f dS y x P L ⎰⎰Γ方法：计算公式191P （1-1）（1-2）（1-3）及推广2.方法①：197P 计算公式（2-1）方法②：y P ≠∂∂林公式非闭：补充曲线后用格闭合：L dxdy y P x Q I L D ⎰⎰∂∂-∂∂=)(y P =∂∂⎰+==),(,1100I 0I y x y x Qdy Pdx L L ）（非闭：闭合：（此时，I 与路径无关，（00,y x ）为起点，（11,y x ）为终点）方法①：199P 计算公式（2-1）的推广方法②：240P 斯托克斯公式（转化为第二类曲面积分）（若方法②使得计算复杂，则不用，一般用方法①）3.第一类曲面积分：dSz y x f ⎰∑),,(方法①：220P 公式（4-2）3种情形.解题步骤：①根据曲面∑选好投影面②确定投影域，曲面∑的显函数形式，并求出dS③将②中三者代入公式，化为二重积分计算.方法②：高斯公式）（'23216P -转为三重积分。

4.第二类曲面积分：⎰⎰∑++RdxdyQdzdx Pdydz 格林公式方法①：228P 计算公式））（）（）（（5545'3535----解题步骤：①代②投③定号（注意曲面的侧定号）方法②：两类曲面积分的联系公式（5P230)cos cos cos (γβαdxdy dzdx dydz dS ===方法③：高斯公式）（16P 232-转化为三重积分三.对面积的曲面积分的计算法思想：化为二重积分就按按照曲面积分的不同情况分为以下三类：（1）若曲面][),(Z xy D xoy y x Z 面，投影区域投影到将：∑∑=（3）若曲面])[,(yz D yoz z y x x 面，投影区域投影到将：∑∑=总结解题步骤：1.应根据曲面∑选好投影面.2.确定投影域并写出曲面∑的显函数形式，并求出dS .3.将曲面∑的显函数形式和dS 代入被积函数，化为二重积分进行计算.小结：与路径无关的四个等价命题条件在单连通区域D上),(),(yxQyxP，具有连续的一阶偏导数，则以下四个命题成立等价命题（1）在D内⎰+LQdyPdx与路径无关（2）⎰=+C,0QdyPdx闭曲线DC⊂（3）在D内存在),,(yxu使QdyPdxdu+=（4）在D内，xQyP∂∂=∂∂感谢高数老师大人的总结！！！。

线面积分的物理意义
线面积分是数学中的一种积分方式，用于对曲线或曲面上的某个量进行求和。

在物理学中，线面积分有以下几个重要的物理意义：
1. 流量：线面积分可以用于计算流量，即单位时间通过曲线或曲面的液体或气体的体积。

例如，在电磁学中，通过一个闭合回路的电流的总量可以通过对该回路上的磁场分布进行线积分来计算。

2. 电荷：线面积分可以用于计算电场或磁场对电荷的影响。

例如，在电动力学中，电场对一个电荷的作用力可以通过电场在电荷路径上的线积分来计算。

3. 能量与功：线面积分可以用于计算能量与功。

例如，在静电学中，电场对一个电荷从一个位置移动到另一个位置所做的功可以通过电场在路径上的线积分来计算。

4. 传热与传质：线面积分可以用于计算传热和传质。

例如，在热力学中，热流通过一个曲面的总量可以通过曲面上的温度梯度进行线积分来计算。

总之，线面积分在物理学中有广泛应用，可以用于描述各种物理量的分布和相互作用。

通过线积分，我们可以更好地理解和分析物理现象，并计算出与这些现象相关的物理量。

习题解读基础阶段的复习是以课本为主，主要任务两个，一是学习知识点（定义、定理、公式）并理解它们，二是完成一定的课后习题以检验自己对知识点的掌握程度。

很多人在学习中都容易忽视课本，觉得比起那些专门的参考资料，课本上的习题实际上是没什么值得关注的，但其实不然，一套经典的教材，它所配的习题很多都有值得我们去挖掘的地方。

那么接下来我就说说我对我们用的教材上课后习题的解读，希望能给同学们提示。

因为高数的题目比较多，而我感觉每章的总习题有着更好的总结性，所以主要就说说总习题一到十二里我感觉值得注意的一些题目吧。

总习题一：1是填空题，是考察与极限有关的一些概念，这个是很重要的，要掌握好。

而且几乎每章的总习题都设了填空题，均与这些章节的重要概念有关。

所以每章的总习题里的填空题所涉及的知识点，比如谁是谁的什么条件之类，务必要搞清楚。

2是无穷小的阶的比较3、4、5、6是与函数有关的题目，这个是学好高数的基础，但却不是高数侧重的内容，熟悉即可7用定义证明极限，较难，一般来说能理解极限的概念就可以了8典型题，求各种类型极限，重要，6个小题各代表一种类型，其实求极限的题目基本跳不出这六种框架了9典型题，选择合适的参数，使函数连续，用连续的定义即可10典型题，判断函数的间断点类型，按间断点的分类即可11较难的极限题，这里是要用到夹逼原理，此类题目技巧性强，体会一下即可12证明零点存在的问题，要用到连续函数介值定理，重要的证明题型之一，必需掌握13该题目给出了渐近线的定义以及求法，要作为一个知识点来掌握，重要综上，第一章总习题要着重掌握的是1、2、8、9、10、12、13题总习题二：1填空题，不多说了，重点2非常好的一道题目，考察了与导数有关的一些说法，其中的干扰项（B）（C）设置的比较巧妙，因为平时我们一般只注意到导数在某点存在的条件是左右导数都存在且相等，容易忽视另一个重要条件：函数必须要在该点连续，否则何来可导？而（B）（C）项的问题正是在于即使其中的极限存在，也不能保证函数在该点连续，因为根本就没出现f(a)，所以对f(x)在a处的情况是不清楚的。

曲线积分与曲面积分1.曲线积分的概念与性质(1)对弧长的曲线积分（又称第一型曲线积分）s y x f Ld ),( ⎰，sz y x f d ),,( ⎰Γ背景曲线L 质量性质线性性可加性(2)对坐标的曲线积分（又称第二型曲线积分）⎰⋅L rF d sF Ld ⎰⋅τ zR y Q x P Ld d d ++⎰sR Q P Ld )cos cos cos ( γβα++⎰这里{}γβατcos ,cos ,cos =为定向曲线的单位切矢量.(具体计算有平面曲线积分与空间曲线积分)背景变力对沿曲线运动的质点做功性质方向性⎰⎰⋅-=⋅-LLrF r Fd d 2.曲线积分的计算公式(1)对弧长的曲线积分设函数),(y x f 在平面曲线,(t) ,(t) :ψϕ==y x L ()βα≤≤t 上连续，)(),(t t ψϕ''在区间[] ,βα上连续，且0)()(22≠'+'t t ψϕ，则[][][]t t t t t f s y x f Ld )()()( ),( d ),(22ψϕψϕβα'+'=⎰⎰,设函数),,(z y x f 在空间曲线),( ),( :t y t x ψϕΓ==),(t z ω=t≤α()β≤上连续，)(),(),(t t t ωψϕ'''在区间[]βα,上连续，且)()(22t t ψϕ'+'0)(2≠'+t ω，则s z y x f d ),,( ⎰Γ[][][][]t t t t t t t f d )()()()( ),( ),( 222 ωψϕωψϕβα'+'+'=⎰.注对弧长的曲线积分化为定积分时,定积分的上限大、下限小．（2）对坐标的曲线积分设L 为:),(),(t y t x ψϕ==α为起点参数，β为终点参数，则y y x Q x y x P Ld ),(d ),( +⎰[]tt t t Q t t t P d )( ))( ),( ()())( ),( ( ⎰'+'=βαψψϕϕψϕ类似地,对于空间曲线)(),(),(:t z t y t x ωψϕΓ===zz y x R y z y x Q x z y x P d ),,(d ),,(d ),,( ++⎰Γ[][]t t t t t Q t t t t t P d )()( ),( ),( d )()( ),( ),( ψωψϕϕωψϕβαβα'+'=⎰⎰[]tt t t t R d )()( ),( ),( ⎰'+βαωωψϕα为起点参数，β为终点参数．（3）全微分式的积分N-L 公式若d (,,)d (,,)d (,,)d u P x y z x Q x y z y R x y z z =++，则(,,)d (,,)d (,,)d (,,)B P x y z x Q x y z y R x y z z u x y z AΓ++=⎰.（4）全微分式求原函数设函数),(y x P ,),(y x Q 在单连通域G 内有连续的一阶偏导数,且xQy P ∂∂=∂∂，则Qdy Pdx +在G 内为某一函数),(y x u 的全微分，且有y y x Q x y x P y x u yy xx d ),(d ),(),( 000⎰⎰+=，(如图11－1(a))或x y x P y y x Q y x u xx yy d ),(d ),(),( 00⎰⎰+=，(如图11－1(b))．3.曲线积分的有关定理定理1(Green 公式)设闭区域D (单或复连通）是由分段光滑的曲线L 围成,函数),(),,(y x Q y x P 在D 上具有连续的一阶偏导数，则有()⎰⎰⎰+=-LDy xy Q x P y x P Qd d d d ，其中L 是D 的取正向的边界曲线．定理2(平面上曲线积分与路径无关的条件)设函数),(y x P ,),(y x Q 在单连通域G 内有连续的一阶偏导数,则以下四个命题等价①⎰+Ly Q x P d d 与路径无关,②),(d d d y x u y Q x P =+,即y Q x P d d +在G 内为某一函数),(y x u 的全微分，d d B AB P x Q y uA+=⎰.③y x P Q ≡,④⎰=+Cy Q x P 0d d ,其中C 为G 内的任意简单闭曲线;4.曲面积分的基本概念与性质（1）对面积的曲面积分（又称第一型曲面积分）Sz y x f Sd ),,(⎰⎰背景曲面质量（2）对坐标的曲面积分（又称第二型曲面积分）指定了侧的曲面称为有向曲面．OOx图11－1(a)y),(00y x A ),(0y x B ),(y x C 图11－1(b)xy ),(00y x A ),(0y x B ),(y x Cz y z y x P d d ),,(⎰⎰∑+x z z y x Q d d ),,(⎰⎰∑+yx z y x R d d ),,(⎰⎰∑⎰⎰∑++SR Q P d )cos cos cos (γβα这里{}γβαcos ,cos ,cos =n为定向曲面的单位法矢量.背景稳定流在单位时间内流过曲面∑一侧的流量⎰⎰∑++=Φy x R x z Q z y P d d d d d d ．性质方向性⎰⎰⎰⎰∑∑-=-.5.曲面积分的计算公式（1）对面积的曲面积分设光滑曲面S 的方程是∑=),,(y x z z 在坐标面xoy 上的投影区域为xy D ，则S z y x f Sd ),,(⎰⎰[]yx z z y x z y x f y x D xyd d 1),(,,22++⋅=⎰⎰（一投二代三微元）（2）对坐标的曲面积分设光滑曲面∑的方程是∑=),,(y x z z 在坐标面xoy 上的投影区域为xy D ，则[]σd ),(,,d d ),,(⎰⎰⎰⎰±=∑xyD y x z y x R y x z y x R （一投二代三定向）∑取上侧时为正，∑取下侧时为负．注当曲面∑是母线平行于z 轴的柱面0),(=y x F 时，0d d ),,(=⎰⎰∑y x z y x R ．统一投影法：若曲面∑可描述为：D y x y x z z ∈=),(),,(，取上（下）侧，则y x R x z Q z y P d d d d d d ⎰⎰∑++{}yx R z Q z P yxd d )()(⎰⎰∑+-⋅+-⋅={}()()d xyx y D P z Q z R σ=±⋅-+⋅-+⎰⎰.6.曲面积分的有关定理定理1（Gauss 公式）设空间闭区域Ω是由分片光滑的闭曲面∑所围成，函数),,(),,,(),,,(z y x R z y x Q z y x P 在Ω上具有一阶连续偏导数，则有()⎰⎰⎰⎰⎰Ω∑++=++yx R x z Q z y P v R QP z yxd d d d d d d 即d d ,F v F n S Ω∑∇⋅=⋅⎰⎰⎰⎰⎰ 其中∑是Ω的整个边界曲面，取外侧（若法矢量n起点在∑上，其指向是离开Ω的）.定理2（Stokes 公式）设Γ为闭曲线,∑是以Γ为边界的有向曲面,Γ的定向与∑的侧向符合右手规则,函数),,(),,,(),,,(z y x R z y x Q z y x P 有一阶连续偏导数，则⎰⎰⎰∑Γ∂∂∂∂∂∂=++RQ P z y x y x x z z y z R y Q x P d d d d d d d d d 或cos cos cos d S x y z PQRαβγ∑∂∂∂=∂∂∂⎰⎰，即d LSF dr F n S ⋅=∇⨯⋅⎰⎰⎰ .其中{}cos ,cos ,cos n αβγ=为定向曲面∑的单位法向量．定理3设空间区域Ω为面单连通区域，{,,}F P Q R =，,,P Q R 在Ω上有连续偏导，则以下四命题等价:(i )积分d LF r ⋅⎰在Ω内与路径无关.(ii )d d d P x Q y R z ++是全微分，即存在(,,)u x y z 使d d d d u P x Q y R z =++.也就是u F ∇=，F 为有势场.(iii )在Ω内0F ∇⨯=,也就是F 为无旋场.(iv )在Ω内沿任意简单闭曲线C ，d 0CF r ⋅=⎰.7.向量场的散度和旋度哈米尔顿算子设向量场由向量kz y x R j z y x Q i z y x P z y x A ),,(),,( ),,(),,(++=给出,其中R Q P ,,有连续的一阶偏导数,则向量场 A 的散度x y z div A P Q R A =++=∇⋅ ．向量场 A 的旋度A rot ij kA x y z PQR∂∂∂==∇⨯∂∂∂ ．哈米尔顿算子运算规则：I （链规则）()()f u f u u '∇=∇，II （积规则）()uv v u u v ∇=∇+∇，()uF u F u F ∇⋅=∇⋅+∇⋅ ，()uF u F u F ∇⨯=∇⨯+∇⨯ .8.Gauss 积分设C 是xoy 平面上简单闭曲线，n是曲线C 在(,)x y 点的单位外法矢量，则cos(,)d C n r I sr =⎰ 称为高斯积分.其中{,}r x y =，||r r == 因为d {d ,d }s x y τ= ，d {d ,d }n s y x =-，高斯积分有变化形式22cos(,){d ,d }d d C C C n r r n r y x s s r r r ⋅⋅-==⎰⎰⎰ 22d d C y x x yx y -+=+⎰ ，高斯积分结果：当C 不包围原点时，0I =；当C 包围原点在其内时，2πI =.面积分中Gauss 积分为2cos(,)d n r I S r ∑=⎰⎰ ,其中n 为曲面∑上在点),,(z y x 处的外法矢量,{,,}r x y z =，r =.变化形式为333d d d d d d x y zI y z z x x y r r r ∑=++⎰⎰，积分结果：当∑不包围原点时，0I =；当∑包围原点在其内时，4πI =.oxyCnτ。