渐开线标准直齿轮

格式：ppt
大小：2.36 MB
文档页数：10

下载文档原格式

/ 10

简述渐开线标准直齿圆柱齿轮机构的正确啮合条件和连续传动条件

简述渐开线标准直齿圆柱齿轮机构的正确啮合条件和连续传动
条件
渐开线是一种特殊的曲线，具有渐开性质，常用于直齿圆柱齿轮的齿廓设计。

渐开线标准直齿圆柱齿轮机构的正确啮合条件和连续传动条件如下：
1. 正确啮合条件：
- 齿轮的模数和压力角必须一致，才能保证正确的啮合。

- 齿轮的齿数必须满足齿轮啮合条件，即两个齿轮间的齿数差必须为一个整数。

2. 连续传动条件：
- 齿轮从一个齿轮转向另一个齿轮时，啮合点必须处于两齿轮的轴线之间，确保齿轮之间的传递力矩连续。

这些条件确保了渐开线标准直齿圆柱齿轮机构的正确啮合和连续传动，从而实现齿轮的平稳运转和可靠传动。

渐开线标准直齿圆柱齿轮的基本参数和

. -任务一、渐开线标准直齿圆柱齿轮各部分名称1、齿顶圆：通过轮齿顶部的圆周。

齿顶圆直径以d a表示。

2、齿根圆：通过轮齿根部的圆周。

齿根圆直径以d f表示。

3、分度圆：齿轮上具有标准模数和标准齿形角的圆。

分度圆直径以d表示。

4、齿厚：在端平面上，一个齿的两侧端面齿廓之间的分度圆弧长。

齿厚以s表示。

5、齿槽宽：在端平面上，一个齿槽的两侧端面齿廓之间的分度圆弧长。

齿槽宽以e表示。

6、齿距：两个相邻且同侧端面齿廓之间的分度圆弧长。

齿距以p表示。

7、齿宽：齿轮的有齿部位沿分度圆柱面直母线方向量度的宽度。

齿宽以b表示。

8、齿顶高：齿顶圆与分度圆之间的径向距离。

齿顶高以h a表示。

9、齿根高：齿根圆与分度圆之间的径向距离。

齿根高以h f表示。

展示多媒体图片，使学生对渐开线标准直齿圆柱齿轮各部分的名称认识更直观。

10、齿高：齿顶圆与齿根圆之间的径向距离。

齿高以h表示。

任务二、渐开线标准直齿圆柱齿轮的基本参数直齿圆柱齿轮的基本参数共有：齿数、模数、齿形角、齿顶高系数和顶隙系数五个，是齿轮各部分几何尺寸计算的依据。

1、齿数z一个齿轮的轮齿总数。

2、模数m齿距与齿数的乘积等于分度圆的周长，即pz=πd,式中z是自然数，π是无理数。

为使d为有理数的条件是p/π为有理数，称之为模数。

即：m=p/π模数的大小反映了齿距的大小，也及时反映了齿轮的大小、已标准化。

模数是齿轮几何尺寸计算时的一个基本参数。

齿数相等的齿轮，模数越大，齿轮尺寸就越大，齿轮就越大，承载能力越强：分度圆直径相等的齿轮，模数越大，承载能力越强。

如图所示：出示教具并提问：模数与轮齿有什么关系？3、齿形角α在端平面上，通过端面齿廓上任意一点的径向直线与齿廓在该点的切线所夹的锐角称为齿形角，用α表示。

渐开线齿廓上各点的齿形角不相等，离基圆越远，齿形角越大，基圆上的齿形角α=0°。

对于渐开线齿轮，通常所说的齿形角是指分度圆上的齿形角。

国标规定：渐开线齿轮分度圆上的齿形角α=20°。

渐开线标准直齿圆柱齿轮各部分的名称及基本参数

第四节渐开线标准直齿圆柱齿轮各部分的名称及基本参数
制作人
一、齿轮各部分的名称
1、齿顶圆：轮齿顶端所在的圆柱面与端面的交线，直径
da
2、齿根圆：轮齿齿根所在的圆柱面与端面的交线。直径 f 3、齿宽：沿齿轮轴线方向量得轮齿宽度b 4、齿厚与齿槽：在齿轮的任意圆周上，一个轮齿两侧间的弧长， sk 称为齿厚，用表示：相邻两齿之间的空间称为齿槽，一个齿槽两侧齿廓在该圆上所截取 ek 的弧长，为齿槽宽，用表示
p = s +e
h
h
h
da
二、直齿圆柱齿轮的基本参数
1、模数m 齿轮齿数z p p dπ= zp ⇒ m = z ⇒ m = ⇒ d = mz π π 2、m越大（p愈大）则齿轮愈大，齿轮抗弯能力也愈高。 * 3、齿顶高系数 ha （正常齿为1，短齿为0.8）和顶隙 * 系数 c （正常齿为0.25，短齿为 0.3） * a a
h = h m
hf = ha m + c m
*
二、直齿圆柱齿轮的基本参数
3、压力角渐开线齿廓上各点的压力角是不相等的，齿廓在分度圆上的压力角称为齿轮的压力角，用α表示，他也是加工轮齿时所用刀具的刀具角，为了便于制造我国规定α=20°。
三、标准直齿圆柱齿轮的几何尺寸计算公式
• 凡齿轮的模数、压力角、齿顶高系数、顶隙系数都是标准值，同时分度圆上齿厚和齿槽相等的齿轮称为标齿轮。计算公式见右表：
dቤተ መጻሕፍቲ ባይዱ
da
一、齿轮各部分的名称
5、分度圆：在齿顶圆和齿根圆之间，直径为d。 6、齿距：沿任意圆周所量得的相邻两齿同侧齿廓之间的弧长，用表示， k p k 7、全齿高、齿根高与齿顶高：分度圆到齿顶圆的径向齿高称为齿顶高，用 a 表示：从分度圆到齿根圆的径向齿高称为齿根高，用 f表示：从齿根圆到齿顶圆的径向齿高称为全齿高，用表示。 8、顶隙：为了防止齿顶齿根相碰，应使齿顶高略小于齿根高，在一轮齿顶到另一轮齿根间留有径向间隙，称为顶隙

渐开线标准直齿轮几何尺寸计算公式

渐开线标准直齿轮几何尺寸计算公式渐开线标准直齿轮几何尺寸计算公式基本参数名称符号公式分度圆直径 d 齿顶高 h a齿根高 h f 全齿高 h 齿顶圆直径 d a (参照注释1) 齿根圆直径 d f (参照注释1) 基圆直径 d b 齿距 p齿厚 s槽宽 e中心距 a (参照注释1) 顶隙 c基圆齿距 p b (参照注释2) 法向齿距 p n注释:1、上面的符号用于外齿轮，下面的符号用于内齿轮;中心距计算公式上面符号用于外啮合齿轮传动,下面符号用于内啮合齿轮传动。

2、因为，所以。

齿轮基本参数:螺纹计算公式1、齿数Z闭式齿轮传动一般转速较高，为了提高传动的平稳性，减小冲击振动，以齿数多一些为好，小一些为好，小齿轮的齿数可取为z1=20~40。

开式(半开式)齿轮传动，由于轮齿主要为磨损失效，为使齿轮不致过小，故小齿轮不亦选用过多的齿数，一般可取z1=17~20。

为使齿轮免于根切，对于α=20o的标准支持圆柱齿轮，应取z1?17。

Z2=u?z1。

2、压力角α rb=rcosα=1/2mzcosα在两齿轮节圆相切点P处，两齿廓曲线的公法线(即齿廓的受力方向)与两节圆的公切线(即P点处的瞬时运动方向)所夹的锐角称为压力角，也称啮合角。

对单个齿轮即为齿形角。

标准齿轮的压力角一般为20”。

在某些场合也有采用α,14.5? 、15? 、22.50?及25?等情况。

3、模数m=p/ π齿轮的分度圆是设计、计算齿轮各部分尺寸的基准，而齿轮分度圆的周长,πd,z p模数m是决定齿轮尺寸的一个基本参数。

齿数相同的齿轮模数大，则其尺寸也大。

4、齿顶高系数和顶隙系数—h*a 、C*两齿轮啮合时，总是一个齿轮的齿顶进入另一个齿轮的齿根，为了防止热膨胀顶死和具有储成润滑油的空间，要求齿根高大于齿顶高。

为次引入了齿顶高系数和顶隙系数。

正常齿:h*a =1; C*=0.25 短齿:h*a =0.8; C*=0.3一般的直齿圆柱齿轮,啮合的条件是:模数相等,压力角相等一、 60?牙型的外螺纹中径计算及公差(国标GB 197/196)a. 中径基本尺寸计算:螺纹中径的基本尺寸=螺纹大径-螺距×系数值公式表示:d/D-P×0.6495例:外螺纹M8螺纹中径的计算8-1.25×0.6495=8-0.8119?7.188b.常用的6h外螺纹中径公差(以螺距为基准)上限值为”0”下限值为P0.8-0.095 P1.00-0.112 P1.25-0.118 P1.5-0.132 P1.75-0.150 P2.0-0.16 P2.5-0.17上限计算公式即基本尺寸,下限值计算公式d2-hes-Td2即中径基本尺寸-偏差-公差M8的6h级中径公差值:上限值7.188 下限值:7.188-0.118=7.07C常用的6g级外螺纹中径基本偏差: (以螺距为基准)P 0.80-0.024 P 1.00-0.026 P1.25-0.028 P1.5-0.032P1.75-0.034 P2-0.038 P2.5-0.042 上限值计算公式d2-ges即基本尺寸-偏差下限值计算公式d2-ges-Td2即基本尺寸-偏差-公差例M8的6g级中径公差值:上限值7.188-0.028=7.16下限值:7.188-0.028-0.118=7.042 注:?以上的螺纹公差是以粗牙为准,对细牙的螺纹公差相应有些变化,但均只是公差变大,所以按此控制不会越出规范界限,故在上述中未一一标出.?螺纹的光杆坯径尺寸在生产实际中根据设计要求的精度和螺纹加工设备的挤压力的不同而相应比设计螺纹中径尺寸加大0.04—0.08之间,为螺纹光杆坯径值,例我们公司的M8外螺纹6g级的螺纹光杆坯径实在7.08—7.13即在此范围.?考虑到生产过程的需要外螺纹在实际生产的未进行热处理和表面处理的中径控制下限应尽量保持在6h级为准二、 60?内螺纹中径计算及公差(GB 197 /196)a. 6H级螺纹中径公差(以螺距为基准)上限值:P0.8+0.125 P1.00+0.150 P1.25+0.16 P1.5+0.180P1.25+0.00 P2.0+0.212 P2.5+0.224 下限值为”0”,上限值计算公式2+TD2即基本尺寸+公差例:M8-6H内螺纹中径为:7.188+0.160=7.348 上限值:7.188为下限值b. 内螺纹的中径基本尺寸计算公式与外螺纹相同即D2=D-P×0.6495即内螺纹中径螺纹大径-螺距×系数值c. 6G级螺纹中径基本偏差E1(以螺距为基准)P0.8+0.024 P1.00+0.026 P1.25+0.028 P1.5+0.032P1.75+0.034 P1.00+0.026 P2.5+0.042例:M8 6G级内螺纹中径上限值:7.188+0.026+0.16=7.374下限值:7.188+0.026=7.214上限值公式2+GE1+TD2即中径基本尺寸+偏差+公差下限值公式2+GE1即中径尺寸+偏差三、外螺纹大径的计算及公差(GB 197/196)a. 外螺纹的6h大径上限值即螺纹直径值例M8为φ8.00上限值公差为”0”b. 外螺纹的6h级大径下限值公差(以螺距为基准)P0.8-0.15 P1.00-0.18 P1.25-0.212 P1.5-0.236 P1.75-0.265P2.0-0.28 P2.5-0.335大径下限计算公式:d-Td 即螺纹大径基本尺寸-公差例:M8外螺纹6h大径尺寸:上限为φ8,下限为φ8-0.212=φ7.788c. 外螺纹6g级大径的计算与公差6g级外螺纹的基准偏差(以螺距为基准)P0.8-0.024 P1.00-0.026 P1.25-0.028 P1.5-0.032 P1.25-0.024 P1.75 –0.034 P2.0-0.038 P2.5-0.042上限计算公式 d-ges 即螺纹大径基本尺寸-基准偏差下限计算公式 d-ges,Td 即螺纹大径基本尺寸-基准偏差-公差例: M8 外螺纹6g级大径上限值φ8-0.028=φ7.972下限值φ8-0.028-0.212=φ7.76注:?螺纹的大径是由螺纹光杆坯径及搓丝板/滚丝轮的牙型磨损程度来决定的,而且其数值在同样毛坯及螺纹加工工具的基础上与螺纹中径成反比出现即中径小则大径大,反之中径大则大径小.?对需进行热处理和表面处理等加工的零件,考虑到加工过程的关系实际生产时应将螺纹大径控制在6h级的下限值加0.04mm以上,如M8的外螺纹在搓(滚)丝的大径应保证在φ7.83以上和7.95以下为宜.四、内螺纹小径的计算与公差a. 内螺纹小径的基本尺寸计算(D1)径基本尺寸=内螺纹基本尺寸-螺距×系数例:内螺纹M8的小径基本尺寸 8-1.25×1.0825=6.646875?6.647b. 内螺纹6H级的小径公差(以螺距为基准)及小径值计算P0.8 +0. 2 P1.0 +0. 236 P1.25 +0.265 P1.5 +0.3 P1.75 +0.335P2.0 +0.375 P2.5 +0.48内螺纹6H级的下限偏差公式D1+HE1即内螺纹小径基本尺寸+偏差注:6H级的下偏值为“0”内螺纹6H级的上限值计算公式=D1+HE1+TD1即内螺纹小径基本尺寸+偏差+公差例:6H级M8内螺纹小径的上限值 6.647+0=6.6476H级M8内螺纹小径的下限值 6.647+0+0.265=6.912c. 内螺纹6G级的小径基本偏差(以螺距为基准)及小径值计算P0.8 +0.024 P1.0 +0.026 P1.25 +0.028 P1.5 +0.032 P1.75 +0.034P2.0 +0.038 P2.5 +0.042内螺纹6G级的小径下限值公式=D1+GE1即内螺纹基本尺寸+偏差例: 6G级M8内螺纹小径的下限值 6.647+0.028=6.6756G级M8内螺纹小径的上限值公式D1+GE1+TD1即内螺纹基本尺寸+偏差+公差例: 6G级M8内螺纹小径的上限值是6.647+0.028+0.265=6.94注:?内螺纹的牙高直接关系到内螺纹的承载力矩的大小,故在毛坯生产中应尽量在其6H级上限值以内?在内螺纹的加工过程中,内螺纹小径越小会给加工具——丝锥的使用效益有所影响.从使用的角度讲是小径越小越好,但综合考虑时一般采用小径的在中限至上限值之间,如果是铸铁或铝件时应采用小径的下限值至中限值之间 ?内螺纹6G级的小径在毛坯生产中可按6H级执行,其精度等级主要考虑螺纹中径的镀层,故只在螺纹加工时考虑丝锥的中径尺寸而不必考虑光孔的小径。

20渐开线标准直齿圆柱齿轮的几何尺寸计算

渐开线标准直齿圆柱齿轮的几何a* m
机
hf =（ha*+ c*）m
械基
正常齿：
础
ha*=1, c*=0.25
短齿：
h顶a*隙=c0＝.8c，*mc*=0.3
es p
c*m
ha
hf
d
O
渐开线标准直齿圆柱齿轮的几何尺寸计算
3 几何尺寸计算
● 标准齿轮：m，α，ha*，c*等于标准数值,齿sz=e
e
B 齿间
(齿槽) sp
机
齿顶高ha ：ha ha*m
pb
械基
齿根高hf ：hf (ha* c* )m
础
齿全高h ：h ha hf
分度圆直径d : d mz
齿顶圆直径da: da d 2ha (z 2ha* )m
d f d 2hf (z 2ha* 2c* )m
齿根圆直径df:
齿轮传动
---渐开线标准直齿圆柱齿轮的几何尺寸计算
渐开线标准直齿圆柱齿轮的几何尺寸计算
1 齿轮各部分名称
基圆 (db, rb) :
产生渐开线的圆
机
齿顶圆da(ra)：
连接齿轮各齿顶的圆
械
基础
齿根圆df(rf):
齿槽底部连接的圆
B
齿z
齿槽
eek
s sk
p pk
齿厚 sk:
在dk圆周上, 一个轮齿左右两侧齿廓间的弧线长
db d cos mz cos
基圆直径db :
O
渐开线标准直齿圆柱齿轮的几何尺寸计算
● 标准齿轮：m，α，ha*，c*等于标准数值, s=e
齿z
B 齿间
齿距p： p m

渐开线标准直齿圆柱齿轮的啮合传动

Machine Design Foundation
渐开线直齿圆柱齿轮
图10-5 渐开线齿轮传动的啮合特性
返回
机械设计基础
Machine Design Foundation
渐开线直齿圆柱齿轮的啮合传动
1．传动比的恒定性由图10-5，可推得齿轮传动的瞬时传动比
i12
1 2
vK1 / O1K vK 2 / O2 K
O1和O2为圆心，过节点P作两个相切的圆，称为节圆。节圆半径r'1=
O1P，r'2= O2P。所以
i12
1 2
rb 2 rb1
r2 ' r1 '
（10-11）
即一对渐开线齿轮传动的瞬时传动比也等于两节圆半径的反比。
2．啮合角的不变性
一对齿轮通过齿廓的直接接触来传递运动和动力，所有啮合点
都在啮合线上。当不计摩擦时，其齿廓间的正压力将沿接触点的公
B2 B1 1
（10-15）
pb
返回
机械设计基础
Machine Design Foundation
渐开线直齿圆柱齿轮的啮合传动
1.4 安装中心距和标准安装中心距
一对外啮合渐开线标准齿轮传动的安装中心距a'是两齿轮节圆
半径之和，即a'=r1'+ r2'。由式（10-1）可得 r'= rb/cosα'，式中α'是节
1.2 渐开线齿轮的正确啮合条件
如图10-6a所示，设相邻两齿同侧齿廓与啮合线（也是公法线）
N1N2的交点分别为K1和K2，线段K1K2的长度称为齿轮的法向齿距。要使两轮正确啮合，它们的法向齿距必须相等。由渐开线的性质可
知，法向齿距等于两轮基圆上的齿距。因此，要使两轮正确啮合，

一对渐开线标准圆柱直齿轮的啮合角

一、概述渐开线标准圆柱直齿轮作为一种常见的传动装置，被广泛应用于机械设备中。

在两个啮合的渐开线标准圆柱直齿轮中，啮合角是一个重要的参数，它直接影响着齿轮传动系统的工作性能。

本文将对渐开线标准圆柱直齿轮的啮合角进行深入分析和探讨。

二、渐开线标准圆柱直齿轮的啮合角1. 定义渐开线标准圆柱直齿轮的啮合角是指两个啮合齿轮齿廓线上法向与渐开线的夹角。

在传动过程中，啮合角反映了两个啮合齿轮之间的啮合条件和啮合方式，是齿轮啮合理论中的重要参数之一。

2. 计算方法渐开线标准圆柱直齿轮的啮合角可以通过几何方法来计算，也可以通过啮合条件和齿轮参数来确定。

一般来说，可以利用啮合角的三角函数表达式来计算啮合角。

啮合角的计算是齿轮设计和分析中的重要环节，需要仔细计算和验证。

3. 影响因素渐开线标准圆柱直齿轮的啮合角受到多种因素的影响，包括齿轮参数、啮合条件、运动状态等。

其中，齿轮压力角、齿轮模数、啮合条件等因素对啮合角的影响较为显著。

在实际设计和应用中，需要充分考虑这些因素，合理确定啮合角的数值。

三、啮合角的作用1. 啮合特性啮合角直接影响着齿轮的啮合性能和传动效率。

合理的啮合角可以使啮合条件良好，减小啮合间隙和啮合失配，减小齿面接触应力，提高传动效率，降低齿轮噪声和振动。

2. 传动性能啮合角还影响着齿轮传动系统的传动性能和工作稳定性。

合适的啮合角可以使齿轮传动系统在工作过程中具有良好的传动特性和稳定性，确保齿轮传动的可靠性和安全性。

3. 对齿轮设计的影响啮合角对齿轮的设计和制造具有一定的指导作用。

合理确定啮合角可以为齿轮的设计提供重要依据，保证齿轮的正常运转和使用性能。

四、啮合角的优化1. 理论分析在设计和优化渐开线标准圆柱直齿轮时，可以通过理论分析和计算来确定最佳的啮合角。

利用啮合角的计算公式和优化方法，可以选择最合适的啮合角，使齿轮传动系统具有最佳的传动效率和工作性能。

2. 模拟仿真借助计算机辅助设计和仿真分析技术，可以对渐开线标准圆柱直齿轮的啮合角进行模拟仿真和优化设计。

正常标准渐开线直齿轮最少齿数

正常标准渐开线直齿轮最少齿数
正常标准渐开线直齿轮最少齿数是一个重要的技术指标，它可以反映出直齿轮的质量和性能。

因此，正确计算正常标准渐开线直齿轮最少齿数对于确保直齿轮的质量和性能具有重要意义。

首先，要计算正常标准渐开线直齿轮最少齿数，必须确定直齿轮的转速、轴向负荷、轴向力矩、轴向摩擦力等参数。

其次，根据直齿轮的转速、轴向负荷、轴向力矩、轴向摩擦力等参数，可以计算出正常标准渐开线直齿轮最少齿数。

此外，正常标准渐开线直齿轮最少齿数的计算还受到直齿轮的材料、精度、硬度等因素的影响。

因此，在计算正常标准渐开线直齿轮最少齿数时，必须考虑到这些因素，以确保计算结果的准确性。

正常标准渐开线直齿轮最少齿数的计算是一个复杂的过程，需要考虑到多种因素，如直齿轮的转速、轴向负荷、轴向力矩、轴向摩擦力等参数，以及直齿轮的材料、精度、硬度等因素。

因此，在计算正常标准渐开线直齿轮最少齿数时，必须综合考虑这些因素，以确保计算结果的准确性。

正常标准渐开线直齿轮最少齿数的计算是一项重要的技术任务，它可以反映出直齿轮的质量和性能。

因此，正确计算正常标准渐开线直齿轮最少齿数对于确保直齿轮的质量和性能具有重要意义。

总之，正常标准渐开线直齿轮最少齿数的计算是一项复杂的任务，需要考虑到多种因素，如直齿轮的转速、轴向负荷、轴向力矩、轴向摩擦力等参数，以及直齿轮的材料、精度、硬度等因素。

因此，在计算正常标准渐开线直齿轮最少齿数时，必须综合考虑这些因素，以确保计算结果的准确性。

只有正确计算正常标准渐开线直齿轮最少齿数，才能确保直齿轮的质量和性能。

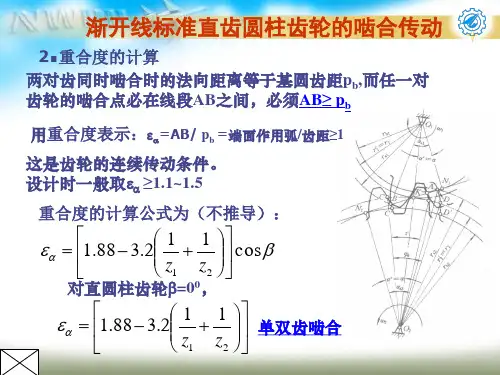
渐开线标准直齿圆柱齿轮的基本参数和几何尺寸计算

(10).齿距(circular pitch)（或称周节） ──相邻两个轮齿同侧齿廓之间在某一个圆上对应点的的圆周弧长。不同圆周上的齿距不同，在半径为rk的圆上，齿距用pk表示，显然有pk=sk+ek；在半径为r 的分度圆上，齿距用p表示，同样p=s+e。若为标准齿轮，则有s=e= 。
❖(11).法向齿距(norm base pitch)──相邻两个轮齿同侧齿廓之间在法线方向上的距离，用pn表示。由渐开线特性可知：pn=pb（基圆齿距）。
传动时一齿轮c的*齿m顶与另一齿轮的齿根相碰撞，而且能贮存润滑油，有利于齿轮的啮
合传动。
§ 1.3标准直齿圆柱齿轮的几何尺寸计算
为避免齿轮传动中出现空程并发生冲击，要求：模数相等节圆与分度圆重合啮合角等于分度圆上压力角，即
' 20
满足上述要求的中心距称为正确安装的标准中心距，用a表示，于是有：
齿顶高和齿根高与模数成正比。所以， ha和hf可分别表示为：
ha ha*m hf (ha* c*)m h*f m
我国标准规定的齿顶高系数 ha’ 和齿根高系hf’数：
系数 ha’
正常齿制 1.0
短齿制 0.8
hf’
1.25
1 .1
❖
称为顶隙，顶隙是一齿轮顶圆与另一齿轮顶圆之间的径向距离。顶隙可避免
计、制造的基准圆，其半径用r表示。
❖(5).齿顶高(addendum)──齿顶圆与
分度圆之间的径向距离，其长度用 ha表示。 (6).齿根高(dedendum)──齿根圆与分度圆之间的径向距离，其长度用hf 表示。
(7).全齿高──齿顶圆与齿根圆之间的径向距离，其长度用h表示，且h=ha+hf。

第5章渐开线标准直齿圆柱齿轮的啮合传动

渐开线标准直齿圆柱齿轮的啮合传动
.2 重合度的计算
两对齿同时啮合时的法向距离等于基圆齿距pb,而任一对齿轮的啮合点必在线段AB之间，必须AB≥ pb
用重合度表示：=AB/ pb =端面作用弧/齿距≥1
这是齿轮的连续传动条件。设计时一般取 ≥1.1~1.5
重合度的计算公式为（不推导）：
1.88
a、范成运动：插刀和轮坯以 i=n刀/ n坯= z坯/ z刀恒定传动比回转，它如同齿轮啮合传动一样。
b、切削运动：插刀沿轮坯轴线作往复切削运动。 c、进给运动：插刀向轮坯中心逐步移动，直至达到规定中心距。
d、让刀运动：为防止损伤切好的齿面，退刀时有一个让刀运动。
同样原理也可用于齿条插刀加工
渐开线齿轮的切齿原理及变位齿轮简介
减轻措施：提高硬度及质量、注意清洁。
齿轮传动的损伤形式及计算准则
4、齿面胶合胶合是相互啮合的轮齿表面在一定的压力下直接接触粘连到一起，同时伴随齿面的相对运动，使金属从齿面上撕落现象。
热胶合重载高速→摩擦热大，油膜破坏→金属熔焊工作面沿滑动方向有撕裂状沟痕，胶合部有颜色变化（回火）。
冷胶合重载低速（未经跑合）→局部压力很大→金属粘着跑合后会消失。
为什么加工精度低？
齿廓形状决定于基圆rb = mzcos ，故m一定，但z不同，齿形
有差异，所以要制造精确，对每一模数于每一种齿数就要准备一把铣刀，就是不可能的。实际情况是一把标准铣刀对应于一定模
数和几种齿数的齿轮。
渐开线齿轮的切齿原理及变位齿轮简介
2、范成法这种方法是利用一对齿轮互相啮合时其轭齿廓互为包络线原理来切齿的。 1）插齿
选材料时要尽量不用合金钢，有些合金元素还要进口，例如过去镍(Ni)要进口，我们就要用三吨对虾去换一吨镍，所以只有在重要场合才用合金钢，要根据具体情况来选用，要尽量节约材料。齿轮材料选择实例二：

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2、直齿圆柱齿轮的主要参数
1)齿数 Z ：一个齿轮的轮齿总数。
2)模数 m：齿距p除以圆周率π所得的商称为模数，即m=P/π，单位
为mm。
a、齿数相等的齿轮，模数越大，尺寸就越大，轮齿也越大，承载能力越强。
b、分度圆直径相等的齿轮，模数越大，承载能力越强，但是齿数越少。
3)压力角：齿廓曲线与分度圆交点处的速度方向与该点法线方向所夹
• 布置作业
一标准直齿圆柱齿轮齿根圆直径df=82.5mm，齿数z=30。试确定该齿轮的主要参数：模数m、分度圆直径d、齿顶圆直径da、齿高h。
锐角，为分度圆上压力角α。规定α =20º 。
4)齿顶高系数ha* :齿顶高* =1。
顶隙系数 c* ：齿轮啮合时，应留有一定的径向间隙，称为顶隙，用
C表示，且C=C* m。规定C*=0.25。
采用标准模数，压力角，齿顶高系数，顶隙系数，分度圆齿厚等于齿槽宽(s＝e)的渐开线直齿圆柱齿轮称为标准直齿圆柱齿轮，简称标准直齿轮。
回忆一下
7.3 渐开线标准直齿轮的基本参数和几何尺寸
7.3.1 直齿圆柱齿轮各部分的名称及主要参数
1、各部分名称 • 齿顶圆da：通过轮齿顶部的圆周。 • 齿根圆df：通过轮齿根部的圆周。 • 分度圆d：齿轮上齿厚和齿槽宽相等的圆。 • 齿厚s：一个轮齿在分度圆上的弧长。 • 齿槽宽e：一个齿槽在分度圆上的弧长。 • 齿距p：两个相邻轮齿的同侧的在分度圆上的弧长。 • 齿宽b：轮齿的宽度。 • 齿顶高ha：齿顶圆与分度圆之间的径向距离。 • 齿根高hf：齿根圆与分度圆之间的径向距离。 • 齿高h：齿顶圆与齿根圆之间的径向距离。
课堂练习：
为修配一个损坏的标准渐开线外齿轮，实测齿轮的齿顶圆直径da=120mm，齿数z=28。试确定该齿轮的主要参数：模数m、分度圆直径d、齿根圆直径df。解： 1)模数：因为 da=m(z+2)，所以 m=da/(z+2)=120/(28+2)=4(mm) 2)分度圆直径d：d=mz=4x28=112(mm) 3)齿根圆直径df：df=m(z-2.5)=4x(28-2.5)=102(mm)
讲评小结和作业
•
本节课学习的主要内容是直齿圆柱齿轮各部分的名称及主要参数，以及各部分几何尺寸计算。通过这次课的学习，我们应该掌握标准直齿圆柱齿轮的主要参数及尺寸（包括：m、d、da、df）的计算，并且学会运用所学知识解决实际问题．本课概念较多，公式也多，但都比较容易理解。希望同学们多花点时间，多做练习，从而更加熟练地应用公式。
7.3.2 渐开线标准直齿圆柱齿轮几何尺寸计算
1、齿顶高：ha=ha*m=m 齿根高：hf=ha+C=(ha*+C*)m=1.25m 齿全高：h=ha+hf=2.25m
2、分度圆径： d=mz（周长=πd=zp）齿顶圆直径：da=d+2ha=mz+2m=m(z+2) 齿根圆直径：df=d-2hf=mz-2X1.25m=m(z-2.5)
3、齿距：p=πm（因为m=P/π） 4、中心距： a=d1/2+d2/2=m(z1+z2) /2 齿厚：s=p/2=πm/2 齿槽宽：e=s=p/2=πm/2 分度圆
P62 例题：已知一渐开线标准直齿圆柱齿轮（正常齿制）模数m=2mm，齿数Z=23，试计算齿轮各部分尺寸。解：因为标准齿轮的参数ha* =1，C*=0.25；m=2mm，z=23。所以各部分尺寸：ha=m=2（mm） hf=1.25m=1.25X2=2.5（mm） h=2.25m=2.25X2=4.5（mm） d=mz=2X23=46（mm） da=m(z+2)=2X(23+2)=50（mm） df=m(z-2.5)=2X(23-2.5)=41（mm） p=πm=3.14X2=6.28（mm） s=e=p/2=3.14（mm）