半角旋转模型
- 格式:doc
- 大小:1.70 MB
- 文档页数:9
专题01 旋转中的三种全等模型(手拉手、半角、对角互补模型)本专题重点分析旋转中的三类全等模型(手拉手、半角、对角互补模型),结合各类模型展示旋转中的变与不变,并结合经典例题和专项训练深度分析基本图形和归纳主要步骤,同时规范了解题步骤,提高数学的综合解题能力。
模型1.手拉手模型【模型解读】将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。
其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
手拉模型解题思路:SAS型全等(核心在于导角,即等角加(减)公共角)。
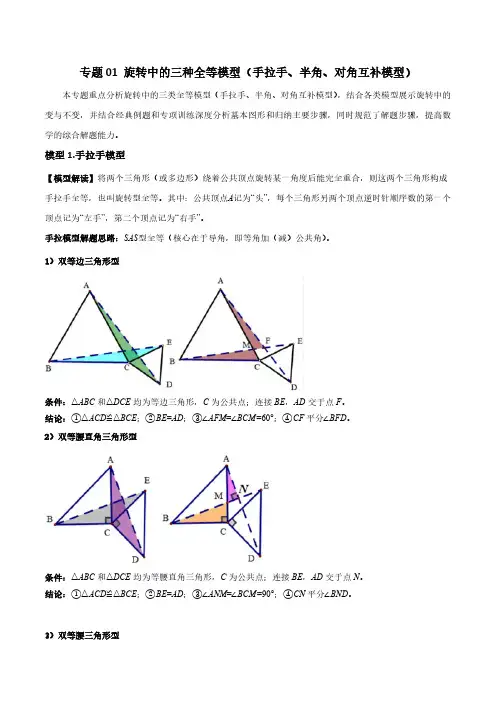
1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。
2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。
结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BND。
3)双等腰三角形型条件:△ABC 和△DCE 均为等腰三角形,C 为公共点;连接BE ,AD 交于点F 。
结论:①△ACD ≌△BCE ;②BE =AD ;③∠ACM =∠BFM ;④CF 平分∠AFD 。
4)双正方形形型条件:△ABCFD 和△CEFG 都是正方形,C 为公共点;连接BG ,ED 交于点N 。
结论:①△△BCG ≌△DCE ;②BG =DE ;③∠BCM =∠DNM=90°;④CN 平分∠BNE 。
例1.(2022·黑龙江·中考真题)ABC V 和ADE V 都是等边三角形.(1)将ADE V 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE V 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE V 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC+=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,PA =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明CAP BAF ≌△△(SAS ),得CAP BAF Ð=Ð,AF AP =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明BAP CAF ≌△△(SAS ),得出CAF BAP Ð=Ð,AP AF =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∵△ABC 是等边三角形,∴AB =AC ,∵点P 与点A 重合,∴PB =AB ,PC =AC ,PA =0,∴PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC=+证明:在BP 上截取BF CP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC CAD DAE CAD Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AC =AB ,CP =BF , ∴CAP BAF ≌△△(SAS ),∴CAP BAF Ð=Ð,AF AP =,∴CAP CAF BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC BAE DAE BAE Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AB =AC ,BP =CF ,∴BAP CAF ≌△△(SAS ),∴CAF BAP Ð=Ð,AP AF =,∴BAF BAP BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.例2.(2023·湖南·长沙市八年级阶段练习)如图1,在Rt △ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE .(1)如图2,将△BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是 ;(2)如图3,DE ∥BC ,连接AE ,判断△EAC 的形状,并求出EC 的长;(3)继续旋转△BDE ,当∠AEC =90°时,请直接写出EC 的长.例3.(2023·黑龙江·虎林市九年级期末)已知Rt △ABC 中,AC =BC ,∠ACB =90°,F 为AB 边的中点,且DF =EF ,∠DFE =90°,D 是BC 上一个动点.如图1,当D 与C 重合时,易证:CD 2+DB 2=2DF 2;(1)当D 不与C 、B 重合时,如图2,CD 、DB 、DF 有怎样的数量关系,请直接写出你的猜想,不需证明.(2)当D 在BC 的延长线上时,如图3,CD 、DB 、DF 有怎样的数量关系,请写出你的猜想,并加以证明.【答案】(1)CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2,证明见解析【分析】(1)由已知得222DE DF =,连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论;(2)连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论.【详解】解:(1)CD 2+DB 2=2DF 2证明:∵DF =EF ,∠DFE =90°,∴222DF EF DE += ∴222DE DF = 连接CF ,BE ,如图∵△ABC 是等腰直角三角形,F 为斜边AB 的中点∴CF BF =,CF AB ^,即90CFB Ð=° ∴45FCB FBC Ð=Ð=°,90CFD DFB Ð+Ð=°又90DFB EFB Ð+Ð=° ∴CFD EFB Ð=Ð在CFD D 和BFE D 中CF BF CFD BFE DF EF =ìïÐ=Ðíï=î∴CFD D @BFED ∴CD BE =,45EBF FCB Ð=Ð=° ∴454590DBF EBF Ð+Ð=°+°=° ∴222DB BE DE +=∵CD BE =,222DE DF =∴CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2 证明:连接CF 、BE∵CF =BF ,DF =EF 又∵∠DFC +∠CFE =∠EFB +∠CFB=90°∴∠DFC =∠EFB ∴△DFC ≌△EFB ∴CD =BE ,∠DCF =∠EBF =135°∵∠EBD =∠EBF -∠FBD =135°-45°=90° 在Rt △DBE 中,BE 2+DB 2=DE 2∵ DE 2=2DF 2 ∴ CD 2+DB 2=2DF 2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键,学会添加常用辅助线,构造全等三角形解决问题.例4.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若ABC V 和ADE V 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =;(2)解决问题:如图2,若ACB △和DCE V 均为等腰直角三角形,90ACB DCE Ð=Ð=°,点A ,D ,E 在同一条直线上,CM 为DCE V 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE Ð=°;2AE AD DE BE CM=+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ≌△CAE ,即可得出结论;(2)同(1)的方法判断出△BAD ≌△CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论.【解析】(1)证明:∵ABC V 和ADE V 是顶角相等的等腰三角形,∴AB AC =,AD AE =,BAC DAE Ð=Ð,∴BAC CAD DAE CAD Ð-Ð=Ð-Ð,∴BAD CAE Ð=Ð.在BAD V 和CAE V 中,AB AC BAD CAE AD AE =ìïÐ=Ðíï=î,∴()BAD CAE SAS ≌△△,∴BD CE =.(2)解:90AEB =°∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE V V ,∴AD BE =,ADC BEC ÐÐ=,∵CDE △是等腰直角三角形,∴45CDE CED Ð=Ð=°,∴180135ADC CDE Ð=°-Ð=°,∴135BEC ADC Ð=Ð=°,∴1354590AEB BEC CED Ð=Ð-Ð=°-°=°.∵CD CE =,CM DE ^,∴DM ME =.∵90DCE Ð=°,∴DM ME CM ==,∴2DE CM =.∴2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ≌△BCE 是解本题的关键.3)15°模型2.半角模型【模型解读】半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半思想方法:通过旋转构造全等三角形,实现线段的转化1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④D AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。

半角旋转模型结论及证明一、引言半角旋转模型是一种常见的物理模型,广泛应用于工程、物理学等领域。
本文将探讨半角旋转模型的结论及其证明,并对其在实际应用中的重要性进行讨论。
二、半角旋转模型的定义半角旋转模型是指一个刚体绕一个固定点旋转的模型,最典型的例子就是地球绕着太阳旋转。
在这种模型中,刚体的转动角度小于180度,即为半角旋转模型。
三、半角旋转模型的结论1. 转动方向:根据右手法则,刚体的转动方向与旋转轴的方向相同。
2. 角速度的变化:根据角动量守恒定律,刚体在旋转过程中,角速度保持不变。
3. 角位移的计算:根据角速度和旋转时间的乘积,可以计算刚体的角位移。
4. 转动惯量的影响:刚体的转动惯量决定了其转动的难易程度。
转动惯量越大,刚体的转动越困难。
四、半角旋转模型的证明1. 转动方向的证明根据右手法则,可以证明刚体的转动方向与旋转轴的方向相同。
右手握住旋转轴,螺旋指向刚体旋转的方向。
2. 角速度的变化的证明根据角动量守恒定律,可以证明刚体在旋转过程中,角速度保持不变。
角动量守恒定律表明,在没有外力矩的情况下,刚体的角动量保持不变,因此角速度也保持不变。
3. 角位移的计算的证明根据角速度和旋转时间的乘积,可以证明刚体的角位移。
角速度定义为单位时间内角度的变化率,因此将角速度乘以旋转时间,得到刚体的角位移。
4. 转动惯量的影响的证明刚体的转动惯量可以通过质量和几何形状来计算。
转动惯量越大,代表刚体的分布越分散,因此刚体的转动越困难。
这一点可以通过实际观察不同形状的物体进行旋转实验来证明。
五、半角旋转模型的实际应用半角旋转模型在工程、物理学等领域有广泛的应用。
例如,对于机械工程师来说,了解半角旋转模型的结论和证明可以帮助他们设计更稳定的旋转机械装置。
在物理学研究中,半角旋转模型提供了理解地球自转、分子旋转等现象的重要工具。
六、结论半角旋转模型是一个常见的物理模型,通过对其结论和证明的讨论,我们可以更深入地理解旋转运动的特性和规律。

半角模型结论及证明过程嘿,朋友!咱们今天来聊聊半角模型,这可有意思啦!你知道吗?半角模型就像是一个藏着宝藏的神秘盒子,一旦你打开它,就能发现里面奇妙的规律。
咱们先来说说半角模型的结论。
比如说一个正方形,有一个角度是正方形内角一半的角,那围绕这个半角产生的一些线段和图形之间,就有着特别的关系。
就像有个例子,正方形 ABCD 边长是 a,∠EAF = 45°,E 在 BC 边上,F 在 CD 边上。
这时候你会发现,EF = BE + DF 。
是不是很神奇?那怎么证明这个结论呢?咱们一步步来。
先把△ABE 绕着点 A 顺时针旋转 90°,让 AB 和 AD 重合,新的点记作 E' 。
这样一转,BE 就变成了 DE' 。
这时候你看,∠EAF = 45°,∠DAE' = 45°,那∠FAE' 不也是 45°吗?再看看△AEF 和△AE'F ,AE = AE' ,AF 是公共边,∠EAF =∠E'AF ,这不就全等了嘛!全等之后,EF 不就等于 E'F 了?而 E'F 正好就是 DE' + DF ,也就是 BE + DF 。
你说这像不像走迷宫,找到一条正确的路,一下子就通了?其实啊,半角模型在很多数学问题里都能派上大用场。
比如说解决一些几何图形的面积问题,或者是判断线段之间的关系。
它就像是一把神奇的钥匙,能打开很多难题的锁。
想想看,如果在考试里遇到这样的题目,你一下子就用半角模型把答案找出来了,那得多厉害,多有成就感啊!所以说,半角模型可是数学里的一个宝贝,咱们可得把它好好掌握,让它成为咱们解题的利器!朋友,你觉得半角模型有趣不?是不是也想多练练,把它用得炉火纯青?。

半角模型十五个结论及证明《探索半角模型的十五个结论及证明》嗨,大家好!今天我要和大家一起探索一个超有趣的数学知识——半角模型的十五个结论及证明。
这就像是一场奇妙的数学冒险,跟我来呀!一、什么是半角模型呢?半角模型呀,就像是一个神秘的数学宝藏,藏在各种几何图形里。
想象一下,我们有一个正方形或者等腰直角三角形,然后在这个图形里出现了一个角,这个角是另外一个大角的一半,这就形成了半角模型。
比如说,在正方形里,一个角是45度,它就是直角90度的一半呢。
这时候啊,就会有好多神奇的结论冒出来。
二、结论一:线段相等我给大家举个例子哈。
在正方形ABCD中,∠EAF = 45度(E、F分别在BC、CD 上)。
我们能发现BE + DF = EF。
这是为啥呢?我们可以把△ADF绕着点A顺时针旋转90度,这样AD就和AB重合了。
旋转后的点F变成了F'。
那这个时候呀,我们就会发现△AEF和△AEF'是全等的。
为啥呢?因为AF = AF',∠EAF = ∠EAF' = 45度,AE是公共边啊。
就像两个一模一样的小积木,那EF就等于EF'了,而EF'就是BE + DF呀。
你们说神奇不神奇?这就好比是把分散的力量集中起来了,原本分开的BE和DF,通过旋转这个魔法,就变成了和EF相等的线段。
三、结论二:三角形面积关系还有一个有趣的结论呢。
三角形AEF的面积等于三角形ABE的面积加上三角形ADF的面积。
这又怎么理解呢?我们刚刚把△ADF旋转到了△ABF'的位置。
那三角形AEF的面积就等于三角形AEF'的面积啦。
而三角形AEF'的面积就是三角形ABE的面积加上三角形ABF'(也就是原来的三角形ADF)的面积。
这就好像是把两个小地块合并起来就等于一个大地块的面积一样。
四、结论三:角平分线如果我们延长CB到G,使得BG = DF,连接AG。
我们会发现AG是∠EAG的角平分线呢。



中考几何模型之半角模型【模型由来】半角模型是指:共顶点的两个一大一小的角,其中小角是大角的一半。
如下图中:若小角∠EAD等于大角∠BAC的一半,我们习惯上称之为“半角模型”。
【模型思想】通过旋转变化后构造全等三角形,实线边的转化。
【基本模型】类型一、90°中夹45°(正方形中的半角模型)条件:在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,BD为对角线,交AE于M点,交AF于N点。
结论①:图1、2中,EF=BE+FD;证明:如图3中,将AF绕点A顺时针旋转90°,F点落在F’处,连接BF’,∴∠EAF’=90°-∠EAF=90°-45°=45°=∠EAF,且AE=AE,AF=AF’,∴△FAE≌△F’AE(SAS),∴EF=EF’,又∠D=∠ABF’=90°,∠ABE=90°,∴∠ABE+∠ABF’=90°+90°=180°,∴F’、B、E三点共线,∴EF’=BE+BF’=BE+DF。
结论②:图2中MN²=BM²+DN²;证明:如图4中,将AN绕点A顺时针旋转90°,N点落在N’处,连接AN’、BN’、MN’,∴∠N’AM=90°-∠EAF=90°-45°=45°=∠MAN,且AM=AM,AN=AN’,∴△MAN’≌△MAN(SAS),∴MN=MN’,又∠ADN=45°=∠ABN ’,∠ABD=45°,∴∠MBN ’=∠ABD+∠ABN ’=45°+45°=90°,∴在Rt △MBN ’中,MN ’²=BM ²+BN ’²,即MN ²=BM ²+BN ’²。
结论③:图1、2中EA 平分∠BEF ,FA 平分∠DFE 。

旋转半角模型条件结论1. 嘿,你知道旋转半角模型的条件吗?就好像拼图的关键一块!比如在正方形 ABCD 中,∠EAF=45°,这就是典型的例子呀!这不是很神奇吗?2. 哎呀呀,旋转半角模型的结论可重要啦!就如同找到了打开宝藏的钥匙。
像三角形 AEF 的面积就等于三角形 ABE 和三角形 ADF 的面积之和,在很多题目里都能看到呢,是不是很厉害?3. 旋转半角模型的条件之一,那可是至关重要的呀!好比是大楼的基石。
比如当有共顶点的等线段时,这就是个明显信号呀,你能想到吗?4. 哇塞,旋转半角模型的结论有时候真让人惊叹!就像突然看到了美丽的彩虹。
像证明某些线段相等,这可太有用了,在那个三角形问题里不就是这样嘛!5. 你瞧,旋转半角模型的条件真的很特别呢!如同黑夜中的一盏明灯。
比如有相等的角,这就是线索呀,你理解了吗?6. 嘿呀,旋转半角模型的结论有时候真的很巧妙!好比是魔术师的神奇魔法。
像得出特殊的角度关系,在那个图形里不就完美呈现了嘛!7. 旋转半角模型的条件,这可是不能忽视的呀!就像前进道路上的指示牌。
例如有特定的图形结构,这不就是关键所在嘛,对不对?8. 哇哦,旋转半角模型的结论真的超有趣!如同发现了一个新的世界。
像找到图形之间的隐藏联系,在那个复杂问题里可派上大用场了呢!9. 旋转半角模型的条件,那可是很有讲究的哟!好像是解开谜题的密码。
比如出现半角的情况,这不就是暗示嘛,你明白了吧?10. 哎呀,旋转半角模型的结论真的会让人眼前一亮!如同看到了璀璨的星星。
像利用结论快速解题,这多棒呀,就像那次我们一起做的那道题一样!我的观点结论就是:旋转半角模型条件结论很重要,我们要好好掌握和运用它呀!。

旋转模型-角含半角模型【内容介绍】本次资料主要包含数学科目,重点指导学生了解旋转模型相关知识,掌握不同旋转模型的解题方法;主要是通过要点梳理,帮助大家综合掌握角含半角模型的含义和解题方法,再通过典型例题的分析,帮助大家了解常考题型。
建议大家深入学习掌握要点梳理,认真研读例题,并在日常学习中注重练习,实现对学习目标的综合把握。
【要点梳理】1)半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半2)思想方法:通过旋转构造全等三角形,实现线段的转化3)基本模型要点一、正方形含半角图1 图2△△△△AEF AEB AFDS S +S )4(;BEF 分平 EA ,DFE 分平 FA )3(;半一的长周形方正是长周的(2) CEF EF=BE+DF;)1(:论结的下以明证,EAF=45,点的上边CD 、BC 是别分F 、E ,中ABCD 形方正在:1图如:题例=∠∠∠︒。
化转的角和段线现实,形角三等全造构转旋过通,型模角半合符,角45有含中角90:析分︒︒△△△△△△△△△AEG AEF AEG AEF G AFE AFD CEF BE BG BE DF AEF AEG AEB AEG AEB AFD 证得S S =S S S S ;证得;证得EF+CE+CF=BE+CE+DF+CF=BC+CD,(2)长周的。
立成=+=+≅∴∠=∠∠=∠=∠∴∴+=+,(4),,,(3)=(1),△△△△△EF EG AEG AEF AE AE AEG AEF EAG EAF AG AF EAG EAF EAF G B C GBC ABG ABC ABG AG AF ABG D BG DF ABCD AD AB ,,中和在,,线共点三、、则,到得,转旋针时顺点沿将,中形方正在,图如:答解∴==∴≅⎩=⎪⎨∠∠⎪⎧=∴∠∠︒∠︒∴∴∠∠+∠︒∠︒∆=∠=∠=︒=∠=︒=︒,===45=45==180ABC =90,90,,GAF 90,2,ADF A 90。

半角模型(一)把过等腰三角形顶角的顶点引两条射线,使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。
1、常见的图形正方形,正三角形,等腰直角三角形等。
特点:①大角内部有一小角,且小角角度是大角角度的一般②大角的两边相等,保证旋转之后能够完全重合③大角的两边与其他两边形成的两个角互补,保证旋转之后的两个三角形两边能在同一直线上2、解题思路①将半角两边的三角形通过旋转到一边合并形成新的三角形;②证明与半角形成的三角形全等;③通过全等的性质得出线段之间的数量关系,从而解决问题。
二、基本模型1、正方形内含半角例题1、如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°,求证:EF=BE+DF。
2、等边三角形内含半角例题2、如图,已知△ABC 是等边三角形,点 D 是△ABC 外一点,DB = DC 且∠BDC = 120°,∠EDF = 60°,DE ,DF 分别交AB ,AC 于点E , F 。
求证:EF = BE + CF3、等腰直角三角形内含半角例题3、如图,已知△ABC 是等腰直角三角形,点D ,E 在BC 上,且满足∠DAE = 45°。
求证:DE^2 = BD^2 + CE^2半角模型练习(二)条件:ABCD为正方形,∠MAN=45°,AM 与AN 分别与BC 边和CD 边交与M,N 两点,连接MN.思路:1、旋转辅助线;①延长CD 到E ,使ED=BM ,连AE 或延长CB 到F ,使FE=DM ,连AF②将三角形AND 绕点A 顺时针旋转90°,得到三角形ABF 。
注意:旋转需证F,B.M 三点共线结论:MN=BM+DN(2)C 三角形CMN=2AB(3)AM,AN 分别平分∠BMN,∠MND2、翻转(对称)辅助线:①做AP 垂直MN ,交MN 于点P②将三角形AND,三角形ABM 分别沿着AM,AM 翻转,但一定要证明M,P ,N 三点共线如图,正方形ABCD 的边长为2,点EF 分别是在AD ,CD 上,若∠EBF=45°,则三角形EDF 的周长等于多少?例题: 已知,如图1,四边形ABCD 是正方形,E 、F 分别在边BC 、CD 上,且∠EAF=45°,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转时一种常用的方法.(1)在图1中,连接EF ,为了证明结论“EF=BE+DF ”,小明将△ADF 绕点A 顺时针旋转90°后解答了这个问题,请按小明的思路写出证明过程; (2)如图2,当∠EAF 的两边分别与CB 、DC 的延长线交于点E 、F ,连接EF ,试探究线段EF 、BE 、DF 之间的数量关系,并证明:。

第4讲 半角模型和其他模型 模块1 半角模型【知识梳理】知识点1 “半角”旋转模型“半角”旋转模型,经常会出现在等腰直角三角形、正方形中,在一般的等腰三角形中也会有涉及.【经典例题】例1 E、F 分别是正方形ABCD 的边BC、CD 上的点,且∠EAF=45°,AH⊥EF, H 为垂足,求证: AH=AB.例2 如图所示,在四边形ABCD 中,AB=BC,∠A=∠C=90°,∠B=135°,K、N 分别是AB AB 、BC 上的点,若△BKN 的周长为AB 的2倍,求∠KDN 的度数.模块2 等腰与辅助线CHFE DB A KNDCB A【知识梳理】知识点2 等腰相关辅助线1.“等腰+垂直=中点+角平分线”若AB=AC,则辅助线可描述为_______________,可以推出________________________,依据是____________________2.“等腰+平行=等腰”若AB=AC,则辅助线可描述为_______________,可以推出________________________,依据是____________________3.“60°造等边”若∠BAC=60°,则辅助线可描述为_______________,可以推出________________________,依据是____________________________________________________________4.“30°+垂直=线段比1:2”若∠BAC=30°,则辅助线可描述为_______________,可以推出________________________,依据是____________________________________________________________【经典例题】例3 如图,在△ABC 中,已知∠ABC =45°,过点C 作CD ⊥AB 于点D ,过点B 作BM ⊥AC 于点M ,CD 与BM 相交于点E ,且点E 是CD 的中点,连接MD ,过点D 作DN ⊥MD ,交BM 于点N .(1)求证:△DBN ≌△DCM ;(2)请探究线段NE 、ME 、CM 之间的数量关系,并证明你的结论.例4 (1)老师在课上给出了这样一道题目:如图1,等边△ABC 边长为2,过AB 边上一点P 作PE ⊥AC 于E ,Q 为BC 延长线上一点,且AP =CQ ,连接PQ 交AC 于D ,求DE 的长.小明同学经过认真思考后认为,可以通过点P 作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE 的长.(2)【类比探究】BCC B老师引导同学继续研究:①等边△ABC边长为2,如图2当P为BA的延长线上一点时,作PE⊥CA的延长线于点E,Q为边BC上一点,且AP=CQ,连接PQ交AC于D.求DE的长并证明.②已知等边△ABC,当P为AB的延长线上一点时,作PE⊥射线AC于点E,Q为BC延长线上一点,且AP=CQ,连接PQ交直线AC于点D,请在图3中补全图形,并证明DE长度保持不变.例5 已知:△ABC中,AB=AC,∠BAC=90°,△ABD为等边三角形,E是BD中点,AE,CD相交于O点.(1)求∠DCB的度数;(2)求证:BC=2DO.例6 如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.(1)依题意补全图形;(2)若∠ACN=α,求∠BDC的大小(用含α的式子表示);(3)用等式表示线段PB,PC与PE之间的数量关系,并证明.附加题1 如图,在△ABC中,AB=AC,D为BC上一点且∠ADC=60°,CE⊥AD于点E,点A关于CE的对称点为点F,CF交AB于点G.(1)依题意补全图形;(2)求∠AGC的度数;(3)写出BD与DF之间的数量关系,并证明.附加题2 已知:如图,等边△ABC和等边△ADE,连接BD、CE交于点O.(1)求证:BD=CE;(2)连接AO,猜想线段AO、BO、CO的数量关系,并证明.【作业】作业1 已知等边△ABC的边长为6,点M是射线AB上的动点,点N是边BC延长线上的动点,在运动的过程中始终满足AM=CN,作MD垂直于射线AC于D,连接MN交射线AC于E.(1)如图1,当点M为AB的三等分点(靠近点A)时,DE的长为 ___.(2)点M、N分别从点A、C同时出发、分别在射线AB、边BC的延长线上以相同的速度开始运动,动点M、N在运动过程中,DE的长会 ____(变小、变大、不变).作业2 如图,在等边三角形ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于Q.求证:(1)△ABE≌△CAD;(2)BP=2PQ.作业3 如图1,已知△ABC是等边三角形,点D是BC边上一点.(1)以AD为边构造等边△ADE(其中点D、E在直线AC两侧),连接CE,猜想CE与AB 的位置关系,并证明你的结论;(2)若过点C作CM∥AB,在CM上取一点F,连AF、DF,使得AF=DF,试猜想△ADF 的形状,并证明你的结论.。
初中数学 ︵ 八年级 ︶培优篇全等三角形在中考数学几何模块中占据着重要地位,也是学生必须掌握的一块内容,本专题就半角模型进行梳理及对应试题分析,方便掌握.半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半. 思想方法:通过旋转(或截长补短)构造全等三角形,实现线段的转化.解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形,从而进行等量代换,然后证明与半角形成的三角形全等,再通过全等的性质得到线段之间的数量关系.半角模型(题中出现角度之间的半角关系)利用旋转——证全等——得到相关结论.【模型展示】 1)正方形半角模型条件:四边形ABCD 是正方形,∠ECF =45°;结论:①△BCE ≌△DCG ;②△CEF ≌△CGF ;③EF =BE +DF ;④ AEF 的周长=2AB ;⑤CE 、CF 分别平分∠BEF 和∠EFD.2)等腰直角三角形半角模型初中数学 ︵ 八年级 ︶培优篇 条件: ABC 是等腰直角三角形,∠DAE =45°;结论:①△BAD ≌△CAG ;②△DAE ≌△GAE ;③∠ECG==90°;④DE 2=BD 2+EC 2;例1.如图,正方形ABCD 中,45MAN ,MAN 绕点A 顺时针旋转,它的两边分别交BC 、DC (或它们的延长线)于点M 、N .(1)当MAN 绕点A 旋转到BM DN 时(如图1),证明:2M N BM ; (2)绕点A 旋转到BM DN 时(如图2),求证:M N BM DN ;例2.如图,在Rt ABC 中,AB AC,45ABCACB ,D 、E 是斜边BC 上两点,且45DAE ∠,若3BD ,4CE ,15ADE S ,则ABD △与AEC △的面积之和为( )A .36B .21C .30D .221)等边三角形半角模型(120°-60°型)初中数学 ︵ 八年级︶培优篇条件: ABC 是等边三角形, BDC 是等腰三角形,且BD =CD ,∠BDC =120°,∠EDF =60°;结论:①△BDE ≌△CDG ;②△EDF ≌△GDF ;③EF =BE +FC ;④ AEF 的周长=2AB ;⑤DE 、DF 分别平分∠BEF 和∠EFC .2)等边三角形半角模型(60°-30°型)例1.在等边△ABC 的两边AB、AC 所在直线上分别有两点M 、N ,D 为△ABC 外一点,且∠MDN =60°,∠BDC =120°,BD =DC .探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系.(1)如图1,当点M 、N 边AB 、AC 上,且DM =DN 时,BM 、NC 、MN 之间的数量关系是 ;(2)如图2,点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想(1)问的结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由.初中数学 ︵ 八年级 ︶培优篇例2.如图,在等边三角形ABC中,在AC 边上取两点M 、N 使30 MBN .若AM m ,MN x ,CN n , 则以x 、m 、n 的为边长的三角形的形状为( )A .锐角三角形B .直角三角形C .钝角三角形D .随x 、m 、n 的值而定例3.如图,△ABC 中,∠BAC =120°,AB =AC ,点D 为BC 边上一点.点E 为线段CD 上一点,且CE =2,AB =DAE =60°,则DE 的长为___.例4.如图,已知△ABC 是边长为4的等边三角形,DBC △是顶角为120°的等腰三角形,动点E 、F 分别在边AB 、AC 上,且60EDF ,则AEF △的周长是( )A .12B .10C .8D .6初中数学 ︵ 八年级 ︶培优篇条件:∠BAC=2 ,AB =AC ,∠DAE = ;结论:①△BAD ≌△CAF ;②△EAD ≌△EAF ;③∠ECF=180°-2 .例1.如图,梯形ABCD 中,AD ∥BC ,AB = BC = DC ,点E 、F 分别在AD 、AB 上,且12FCE BCD. (1)求证:BF EF ED ;(2)连结AC ,若80,70B DEC ,求ACF 度数.1.如图,在边长为5的正方形ABCD 内作45EAF =,AE 交BC 于点E ,AF 交CD 于点F ,连接EF .若2DF ,则BE 的长为( )初中数学 ︵ 八年级 ︶培优篇A.157B .432.如图,正方形ABCD 中,点E 、F 分别在线段BC 、CD 上运动,且满足∠EAF =45°,AE 、AF 分别与BD 相交于点M 、N ,下列说法中:①BE +DF =EF ;②点A 到线段EF 的距离一定等于正方形的边长;③BE =2,DF =3,则S △AEF =15;④若AB =,BM =3,则MN =5.其中结论正确的个数是( )A .4B .3C .2D .13.如图,已知正方形ABCD 的边长为5,点E ,F 分别是AB ,BC 边上的点,且∠EDF =45°,将△ADE 绕点D 逆时针旋转90°得到△CDM .若AE =2,则MF 的长为_______.4.在等边三角形ABC 中.初中数学 ︵ 八年级 ︶培优篇(1)如图1,D 、E 是边BC 上两动点,且∠DAE =30°,将△ABE 绕点A 逆时针旋转60°后,得到△ACF ,连接DF ;①求证:△AED ≌△AFD ;②当BE =2,CE =5时,求DE 的长;(2)如图2,点D 是等边三角形ABC 的边BC 所在直线上的一动点,连接AD ,将线段AD 绕点A 顺时针旋转60°得到线段AE ,连接CE ,当BD =2,BC =6时,CE 的长为________.。
八年级上册数学半角模型
半角模型是指以等腰三角形顶角的顶点为端点,引两条射线,与等腰三角形顶角相邻的边重合,这两条射线所形成的夹角为等腰三角形顶角的一半。
在八年级上册的数学中,半角模型可以用于解决一些几何问题。
例如,在一个等边三角形ABC中,点D是BC的中点,连接AD并延长到E 点,使得DE等于AE。
求证:角BAE等于角BCE。
这个问题可以通过半角模型来解决。
首先,将三角形ABD绕点A旋转到三角形ACD'的位置,使得AD'与AE重合。
由于旋转过程中只改变了角度,所以旋转前后的图形全等,因此角BAE等于角D'CE。
而由于DE等于AE,所以角D'CE 等于角BCE。
因此,角BAE等于角BCE。
总之,半角模型是一种有用的几何工具,可以用于证明一些等角、等线段的问题。
旋转中的几何模型模型一角含半角模型模型特征:角含半角模型,顾名思义即一个角包含着它的一半大小的角。
它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。
解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。
1综合与实践:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF= 45°,连接EF,求证:DE+BF=EF.李伟同学是这样解决的:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,再证明△GAF≌△EAF,可得结论.(1)如图2,在四边形ABCD中,AD∥BC AD>BC,∠D=90°,AD=CD=10,且∠BAE= 45°,DE=4,求BE的长;(2)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD2+CE2=DE2始终成立,请说明理由.【思路点拨】(1)过A作AG⊥BC,交BC延长线于G,由正方形的性质得出CG=AD=10,再运用勾股定理和方程求出BE的长;(2)运用旋转性质和勾股定理判断说明等式成立.【解题过程】解:(1)如图2,过点A作AG⊥BC,交CB延长线于点G.四边形ADCG中,∠D=∠C=∠G=90°,AD=DC,∴四边形ADCG是正方形.∴CG=AD=10.已知∠BAE=45°,根据已知材料可得:BE=GB+DE.设BE=x,则BG=x-4,∴BC=14-x.在Rt△BCE中,BE2=BC2+CE2,∴x2=14-x2+62,解得x=58 7.∴BE=587.(2)如图3,将△ACE绕点A顺时针旋转90°至△ABH位置,则CE=BH,AE=AH,∠ABH=∠C=45°,旋转角∠EAH=90°.连接HD,在△EAD和△HAD中,AE=AH∠HAD=∠EAD AD=AD,∴△EAD≌△HAD SAS.∴DH=DE.又∠HBD=∠ABH+∠ABD=90°,∴BD2+BH2=HD2,∴BD2+CE2=DE2.2如图,△ABC中,AB=AC,∠BAC=90°,点D、E在BC边上,∠DAE=45°,将△ACE绕点A顺时针旋转90°得△ABF.(1)求证:BF⊥BC;(2)连接DF,求证:△ADF≌△ADE;(3)若BD=3,CE=4,则DF=,四边形AFDE的面积=.【思路点拨】(1)由旋转的性质得∠C=∠ABF,从而得到∠DBF=∠ABC+∠ABF=90°,即可证明结论;(2)由旋转的性质得AF=AE,∠BAF=∠CAE,则∠BAD+∠BAF=∠BAD+∠CAE=45°,再利用SAS即可证明;(3)如图,过点A作AH⊥BC于H,由(1)得,∠DBF=90°,在Rt△DBF中,由勾股定理得DF= BD2+BF2=32+42=5,则BC=BD+DF+CE=3+5+4=12,再根据直角三角形斜边上的中线等于斜边的一半求出AH,再利用S四边形AFDE=2S△ADE可得出答案.【解题过程】(1)证明:∵将△ACE绕点A顺时针旋转90°得△ABF,∴∠C=∠ABF,∵在△ABC中,AB=AC,∠BAC=90°,∴∠ABC=∠C=45°,∴∠DBF=∠ABC+∠ABF=45°+45°=90°,∴BF⊥BC.(2)证明:∵将△ACE绕点A顺时针旋转90°得△ABF,∴AF=AE,∠BAF=∠CAE,∵∠DAE=45°,∠BAC=90°,∴∠BAD+∠CAE=90°-45°=45°,∴∠BAD+∠BAF=∠BAD+∠CAE=45°,∴∠DAF=∠DAE,在△ADF和△ADE中,AF=AE∠DAF=∠DAE AD=AD,∴△ADF≌△ADE SAS.(3)解:如图,过点A作AH⊥BC于H,∵将△ACE绕点A顺时针旋转90°得△ABF,BD=3,CE=4,∴BF=CE=4,由(1)得,∠DBF=90°,在Rt△DBF中,DF=BD2+BF2=32+42=5,由(2)得,△ADF≌△ADE,∴DE=DF=5,S△ADF=S△ADE,∴BC=BD+DE+CE=3+5+4=12,∵在△ABC中,AB=AC,∠BAC=90°,AH⊥BC∴BH=CH,∴AH=12BC=6,∴四边形AFDE的面积:S四边形AFDE=S△ADF+S△ADE=2S△ADE=2×12×DE×AH=DE×AH=5×6=30.故答案为:5;30.针对训练13如图,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°,分别连接EF、BD,BD与AF、AE分别相交于点M、N(1)求证:EF=BE+DF为了证明“EF=BE+DF”,小明延长CB至点G,使BG=DF,连接AG,请画出辅助线并按小明的思路写出证明过程.(2)若BE=2,DF=3,请求出正方形ABCD的边长.(3)请直接写出线段BN、MN、DM三者之间的数量关系【分析】(1)延长BC 到G ,使BG =DF ,连接AG ,证得△ABG ≌△ADF ,△AEF ≌△AEG ,最后利用等量代换求得答案即可;(2)根据(1)中的结论,设正方形的边长为x ,列方程可解答;(3)在AG 截取AH =AM ,连接NH 、BH ,证得△ABH ≌△ADM ,△AMN ≌△AHN ,最后利用勾股定理求得答案即可.【解析】(1)证明:如图1,延长CB 至点G ,使BG =DF ,连接AG,∵四边形ABCD 为正方形,∴AB =AD ,∠BAD =∠ADF =∠ABE =∠ABG =90°,在△ABG 和△ADF 中,AB =AD ∠ABG =∠ADF BG =DF,∴△ABG ≌△ADF (SAS ),∴∠DAF =∠BAG ,AF =AG ,∴∠GAE =∠BAG +∠BAE =∠DAF +∠BAE =90°-45°=45°=∠EAF ,在△AEF 和△AEG 中,AF =AG ∠FAE =∠GAE AE =AE,∴△AEF ≌△AEG (SAS ),∴EF =EG ,∵EG =BE +BG ,∴EF =BE +DF ;(2)解:设正方形的边长为x ,∵BE =2,DF =3,∴CE =x -2,CF =x -3,由(1)得:EF =BE +DF =2+3=5,Rt △CEF 中,EF 2=CE 2+CF 2,52=(x -2)2+(x -3)2,解得:x =6或-1(舍),答:正方形ABCD 的边长为6.(3)解:BN 2+DM 2=MN 2;理由是:如图2,在AG 上截取AH =AM ,连接HN 、BH ,在△AHB 和△AMD 中,AB =AD ∠HAB =∠MAD AH =AM,∴△AHB ≌△AMD (SAS ),∴BH =DM ,∠ABH =∠ADB =45°,又∵∠ABD =45°,∴∠HBN =90°.∴BH 2+BN 2=HN 2.在△AHN 和△AMN 中,AH =AM ∠HAN =∠MAN AN =AN,∴△AHN ≌△AMN (SAS ),∴MN =HN .∴BN 2+DM 2=MN 2.4如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE .(1)求证:CE =CF ;(2)在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么?(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题:①如图2,在四边形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =6,E 是AB 的中点,且∠DCE =45°,求DE 的长;②如图3,在△ABC 中,∠BAC =45°,AD ⊥BC ,BD =4,CD =6,则△ABC 的面积为60(直接写出结果,不需要写出计算过程).【分析】(1)因为ABCD 为正方形,所以CB =CD ,∠B =∠CDA =90°,又因为DF =BE ,则△BCE ≌△DCF ,即可求证CE =CF ;(2)因为∠BCD =90°,∠GCE =45°,则有∠BCE +∠GCD =45°,又因为△BCE ≌△DCF ,所以∠ECG =∠FCG ,CE =CF ,CG =CG ,则△ECG ≌△FCG ,故GE =BE +GD 成立;(3)①过点C 作CG ⊥AD 交AD 的延长线于点G ,利用勾股定理求得DE 的长;②由题中条件,建立图形,根据已知条件,运用勾股定理,求出AD 的长,再求得△ABC 的面积.【解析】(1)在正方形ABCD 中CB =CD ,∠B =∠CDA =90°,∴∠CDF =∠B =90°.在△BCE 和△DCF 中,CB =CD ∠B =∠CDF BE =DF,∴△BCE ≌△DCF (SAS ).∴CE =CF .(2)GE =BE +GD 成立.理由如下:∵∠BCD =90°,∠GCE =45°,∴∠BCE +∠GCD =45°.∵△BCE ≌△DCF (已证),∴∠BCE =∠DCF .∴∠GCF =∠GCD +∠DCF =∠GCD +∠BCE =45°.∴∠ECG =∠FCG =45°.在△ECG 和△FCG 中,CE =CF ∠ECG =∠FCG CG =CG,∴△ECG ≌△FCG (SAS ).∴GE =FG .∵FG =GD +DF ,∴GE =BE +GD .(3)①如图2,过点C 作CG ⊥AD ,交AD 的延长线于点G ,由(2)和题设知:DE =DG +BE ,设DG =x ,则AD =6-x ,DE =x +3,在Rt △ADE 中,由勾股定理得:AD 2+AE 2=DE 2,∴(6-x )2+32=(x +3)2,解得x =2.∴DE =2+3=5;②如图3,将△ABD 沿着AB 边折叠,使D 与E 重合,△ACD 沿着AC 边折叠,使D 与G 重合,可得∠BAD =∠EAB ,∠DAC =∠GAC ,∴∠EAG =∠E =∠G =90°,AE =AG =AD ,BD =EB =4,DC =CG =6,∴四边形AEFG 为正方形,设正方形的边长为x ,则BF =x -4,CF =x -6,在Rt △BCF 中,根据勾股定理得:BF 2+CF 2=BC 2,即(x -4)2+(x -6)2=(4+6)2,解得:x =12或x =-2(舍去),∴AD =12,∴S △ABC =12BC •AD =12×10×12=60.故答案为:60拓展类型 构造旋转模型解题方法指导:若一个图形中含有相等的线段和特殊的角度,通常是以等线段的公共端点为旋转中心进行旋转,使得相等的边重合,得出特殊的图形.1请阅读下列材料:问题:如图1,在等边△ABC 内有一点P ,且PA =2,PB =3,PC =1,求∠BPC 的度数和等边△ABC 的边长.李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠BPC =∠AP′B=150°,进而求出等边△ABC的边长为7,问题得到解决.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA= 5,BP=2,PC=1.求∠BPC的度数和正方形ABCD的边长.解:将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A.∴AP′=PC=1,BP′=BP=2.易证∠PBP′=∠ABC=90°.连接PP′,在Rt△BP′P中,∵BP=BP′=2,∠PBP′=90°,∴PP′=2,∠BP′P=45°.在△AP′P中,AP′=1,PP′=2,AP=5,∵12+22=(5)2,即AP′2+PP′2=AP2,∴△AP′P是直角三角形,即∠AP′P=90°.∴∠AP′B=∠AP′P+∠BP′P=135°.∴∠BPC=∠AP′B=135°.过点B作BE⊥AP′,交AP′的延长线于点E,则△BEP′是等腰直角三角形.∵BP′=2,∴EP′=BE=1.∴AE=2.∴在Rt△ABE中,由勾股定理,得AB=5.∴∠BPC=135°,正方形ABCD的边长为5.2如图1,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.(1)求证:EB=GD且EB⊥GD;(2)若AB=2,AG=2,求BE的长;【答案】(1)见解析;(2)10;(3)不变,△ABG与△DAE的面积之差为0【分析】(1)在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,得到∠GAD=∠EAB,从而△EAB≌△GAD,即EB=GD;由∠AEB=∠AGD,∠EOH=∠AOG,即可得出∠EHG=∠EAG=90°;(2)设BD与AC交于点O,由AB=AD=2,在Rt△ABD中求得DB,在Rt△GOD中利用勾股定理即可求得结果;【详解】(1)如图1,∵四边形EFGA和四边形ABCD是正方形,∴AG=AE,AB=AD,∠EAG=90°,∠DAB=90°,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,∴∠GAD=∠EAB,在△EAB和△GAD中,AB=AD∠EAB=∠GAD AE=AG,∴△EAB≌△GAD(SAS),∴EB=GD;∠AEB=∠AGD,∵∠EOH=∠AOG,∴∠EHG=∠EAG=90°,∴EB=GD且EB⊥GD;(2)如图2,连接BD,BD与AC交于点O,∵AB=AD=2,在Rt△ABD中,DB=AB2+AD2=22+22=22,∴AO=DO=2,∴OG=OA+AG=2+2=22,∴EB=GD=OG2+OD2=222+22=10;【点睛】本题考查了正方形的性质及全等三角形的判定与性质、勾股定理、三角形外角的性质,作出辅助线,利用三角形全等是解题的关键.针对训练25以△ABC的AB、AC为边作△ABD和△ACE,且AE=AB,AC=AD,CE与BD相交于M,∠EAB=∠CAD=α.(1)如图1,若α=40°,求∠EMB 的度数;(2)如图2,若G 、H 分别是EC 、BD 的中点,求∠AHG 的度数(用含α式子表示);(3)如图3,连接AM ,直接写出∠AMC 与α的数量关系是 90°+12α .【分析】(1)由“SAS ”可证△AEC ≌△ABD ,可得∠AEC =∠ABD ,由外角的性质可得结论;(2)由“SAS ”可证△ACG ≌△ADH ,可得AG =AH ,∠CAG =∠DAH ,即可求解;(3)由全等三角形的性质可得S △ACG =S △ADH ,EC =BD ,由面积法可求AP =AN ,由角平分线的性质可求∠AMD ,即可求解.【解答】解:(1)∵∠EAB =∠CAD =α,∴∠EAC =∠BAD ,在△AEC 和△ABD 中,AE =AB ∠EAC =∠BAD AC =AD,∴△AEC ≌△ABD (SAS ),∴∠AEC =∠ABD ,∵∠AEC +∠EAB =∠ABD +∠EMB ,∴∠EMB =∠EAB =40°;(2)连接AG ,AH ,由(1)可得:EC =BD ,∠ACE =∠ADB ,∵G 、H 分别是EC 、BD 的中点,∴DH =CG ,在△ACG 和△ADH 中,AC =AD ∠ACE =∠ADB CG =DH,∴△ACG ≌△ADH (SAS ),∴AG =AH ,∠CAG =∠DAH ,∴∠AGH =∠AHG ,∠CAG -∠CAH =∠DAH -∠CAH ,∴∠GAH =∠DAC ,∵∠DAC =α,∴∠GAH =α,∵∠GAH +∠AHG +∠AGH =180°,∴∠AHG =90°-12α;(3)如图3,连接AM ,过点A 作AP ⊥EC 于P ,AN ⊥BD 于N ,∵△ACE ≌△ADB ,∴S △ACE =S △ADB ,EC =BD ,∵12EC ×AP =12×BD ×AN ,∴AP =AN ,又∵AP ⊥EC ,AN ⊥BD ,∴∠AME =∠AMD =180°-α2,∴∠AMC =∠AMD +∠DMC =90°+12α,故答案为:90°+12α.6在△ABC 中,∠BAC =90°,AC =AB ,点D 为直线BC 上的一动点,以AD 为边作△ADE (顶点A 、D 、E 按逆时针方向排列),且∠DAE =90°,AD =AE ,连接CE .(1)如图1,若点D 在BC 边上(点D 与B 、C 不重合),①求证:△ABD ≌△ACE ;②求证:DE 2=BD 2+CD 2(2)如图2,若点D 在CB 的延长线上,若DB =5,BC =7,则△ADE 的面积为.(3)如图3,若点D 在BC 的延长线上,以AD 为边作等腰Rt △ADE ,∠DAE =90°,连结BE ,若BE =10,BC =6,则AE 的长为.【答案】(1)①见解析;②见解析;(2)1694;(3)34【分析】(1)①根据∠BAC =∠DAE ,推出∠BAD =∠CAE ,再结合AB =AC ,AD =AE ,即可证明△ABD ≌△ACE ,②根据∠ABD =∠ACE ,可得∠ABD +∠ACB =∠ACE +∠ACB =∠BCE ,根据BD =CE ,即可证明结论;(2)过点A 作AF ⊥DE 于点F ,利用等腰三角形的性质和直角三角形的性质,易得AF =12DE ,利用全等三角形的判定定理可得△ABD ≌△ACE ,由全等三角形的性质可得∠ADB =∠AEC ,DB =EC ,易得EC =5,DC =12,利用勾股定理可得DE 的长,利用三角形的面积公式可得结论;(3)根据Rt △BCE 中,BE =10,BC =6,求得CE =102-62=8,进而得出CD =8-6=2,在Rt △DCE 中,求得DE =22+82=68,最后根据△ADE 是等腰直角三角形,即可得出AE 的长.【详解】(1)①∵∠BAC =∠DAE ,∴∠BAD =∠CAE ,又∵AB =AC ,AD =AE ,∴△ABD ≌△ACE ,②∵△ABD≌△ACE,∴∠ABD=∠ACE,BD=CE,∴∠ABD+∠ACB=∠ACE+∠ACB=∠DCE=90°,∴DE2=CD2+CE2=CD2+BD2;(2)过点A作AF⊥DE于点F.∵AD=AE,∴点F是DE的中点,∵∠DAE=90°,∴AF=12DE,同理可证△ABD≌△ACE,∴∠ADB=∠AEC,DB=EC,∵DB=5,BC=7,∴EC=5,DC=12,∵∠DAE=90°,∴∠ADE+∠AED=90°,∴∠ADC+∠CDE+∠AED=90°,∴∠AEC+∠AED+∠CDE=90°,即∠CED+∠CDE=90°,∴∠ECD=90°,∴DE2=CE2+CD2=25+144=169,∵DE>0,∴DE=13,∴AF=132,∴△ADE的面积为=12DE•AF=12×13×132=1694;(3)由(1)可知:△ABD≌△ACE,∴BD=CE,∠ABD=∠ACE,∴∠BCE=∠ACB+∠∠ACE=∠ACB+∠ABD=90°,∴Rt△BCE中,BE=10,BC=6,∴CE=102-62=8,∴BD=CE=8,∴CD=8-6=2,∴Rt△DCE中,DE=22+82=68,∵△ADE是等腰直角三角形,∴AE=DE2=682=34.【点睛】本题主要考查了全等三角形的判定定理及性质定理,还有等腰三角形的性质等,综合利用定理,作出恰当的辅助线是解答此题的关键.巩固练习1已知在△ABC中,BC=4。
小伟遇到这样一个问题:如图 1,在正方形 ABCD 中,点 E 、F 分别为 DC 、BC 边上的点,/ EAF =45° ,连结 EF ,求证: DE+BF=EF .小伟是这样思考的: 要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段△ ADE 绕点A 顺时针旋转 90得到△ ABG (如图2),此时GF 即是DE + BF . 请回答:在图2中,/ GAF 的度数是 参参考小伟得到的结论和思考问题的方法,解决下列问题:D (1)如图3C 在直角梯形 ABCD E 中, A•内容:半角旋转模型,三垂直模型,以及旋转相似模型探究:(1)如图1,在正方形 ABCD 中,E 、F 分别是BC 、CD 上的点,且/ EAF = 45 ° 试判断 BE 、DF 与 EF 三条线段之间的数量关系,直接写出判断结 果: ;(2) 如图2,若把(1)问中的条件变为 在四边形ABCD 中,AB = AD , / B + Z D = 180° E 、1F 分别是边BC 、CD 上的点,且/ EAF= — / BAD ,则(1)问中的结论是否仍然成立?若2成立,请给出证明,若不成立,请说明理由;(3) 在(2)问中,若将△ AE F 绕点A 逆时针旋转,当点分别 E 、F 运动到BC 、CD 延长 线上时, 如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予 以证明..R E CB图1OCBx图3B 图4上•他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题•他的方法是将 图3AD // BC (AD >BC ),/ D=90° AD=CD=10, E 是 CD 上一点,若/ BAE=45° DE=4,贝U BE= _________________ .(2)如图4,在平面直角坐标系 xOy 中,点B 是x 轴上一 动点,且点 A ( _3,2),连结AB 和AO ,并以AB 为边向上作 正方形ABCD ,若C ( x ,y ),试用含x 的代数式表示y , 贝 y y= .已知:正方形 ABCD 中, .MAN =45;,绕点A 顺时针旋转,它的两边分别交 CB 、DC(或它们的延长线)于点M 、N .(1)如图1,当.MAN(2)当.MAN 绕点A 旋转到如图3的位置时,线段BM , DN 和MN 之间有怎样的等量关系?请写出你的猜想, 并证明.绕点A 旋转到BM 二DN 时,有BM DN 二MN •当.MAN绕点A 旋转到BM = DN 时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;24.如图1,在等腰直角 △ ABC 中,/ BAC=90 ° AB=AC=2,点E 是BC 边上一点,/ DEF =45 ° 且角的两边分别与边 AB ,射线CA 交于点P, Q.(1) 如图2,若点E 为BC 中点,将/ DEF 绕着点E 逆时针旋转,DE 与边AB 交于点P,EF 与CA 的延长线交于点 Q.设BP 为x, CQ 为y,试求y 与x 的函数关系式,并写 出自变量x 的取值范围;(用含k 的代数式表示);(2) (2)如图3,点E 在边BC 上沿B 到C 的方向运动(不与 B, C 重合),且DE 始终经过 点A,EF 与边AC 交于Q 点•探究:在/ DEF 运动过程中,△ AEQ 能否构成等腰三 角形,若能,求出 BE 的长;若不能,请说明理由.海淀25.如图1,两个等腰直角三角板 ABC 和DEF 有一条边在同一条直线 I 上, DE = 2 , AB =1 .将直线EB 绕点E 逆时针旋转45 ,交直线AD 于点M •将图1中的三角板ABC 沿直线I 向右平移,设 C 、E 两点间的距离为k .①当点C 与点F 重合时,如图2所示,可得 如 的值为DM②在平移过程中,如的值为DM将图2中的三角板 ABC 绕点C 逆时针旋转,原题中的其他条件保持不变•当点A 落在线段DF 上时,如图3所示,请补全图形,计算 如 的值;DM(3)将图1中的三角板ABC 绕点C 逆时针旋转:-度,0::: : <90,原题中的其他条件保 持不变•计算如的值(用含k 的代数式表示)DM图3图3(1)BAP C ,连接PP',得到两昌平22.阅读下面材料:小伟遇到这样一个问题:如图1 ,在正三角形 ABC 内有一点 P,且PA=3 , PB=4 , PC=5,求/ APB 的度数.小伟是这样思考的:如图 2,利用旋转和全等的知识构造△个特殊的三角形,从而将问题解决.请你回答:图1中/APB 的度数等于 ___________ .参考小伟同学思考问题的方法,解决下列问题:(1) 如图 3,在正方形 ABCD 内有一点 P,且 PA=2、、2, PB=1 , PD=、_17,则/ APB 的 度数等于 _____ ,正方形的边长为 _______ ;(2) 如图4,在正六边形 ABCDEF 内有一点 P,且FA= 2 , PB=1, PF=、_13,则/ APB 的 度数等于 _____ ,正六边形的边长为 ________ .通州24. ( 9分)在平面直角坐标系 xOy 中,点B(0, 3),点C 是x 轴正半轴上一点,连结 BC ,过点C 作直线CP // y 轴.(1) 若含45。
.内容:半角旋转模型,三垂直模型,以及旋转相似模型探究:(1)如图1,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45°,试判断BE 、DF 与EF 三条线段之间的数量关系,直接写出判断结果: ;(2)如图2,若把(1)问中的条件变为“在四边形ABCD 中,AB =AD ,∠B +∠D =180°,E 、F 分别是边BC 、CD 上的点,且∠EAF=21∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;(3)在(2)问中,若将△AE F 绕点A 逆时针旋转,当点分别E 、F 运动到BC 、CD 延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明..小伟遇到这样一个问题:如图1,在正方形ABCD 中,点E 、F 分别为DC 、BC 边上的点,∠EAF =45°,连结EF ,求证:DE +BF =EF .小伟是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段集中到同一条线段上.他先后尝试了平移、翻折、旋转的方法,发现通过旋转可以解决此问题.他的方法是将△ADE 绕点A 顺时针旋转90°得到△ABG (如图2),此时GF 即是DE +BF .请回答:在图2中,∠GAF 的度数是 .参考小伟得到的结论和思考问题的方法,解决下列问题:(1)如图3,在直角梯形ABCD 中,AD ∥BC (AD >BC ),F ED AB C B EDA G F D AB C C图1图2图3CDAOBx y 图4F E D A B C B EDA G F E D ABC C图1图2图3CD AO B x y 图4∠D =90°,AD =CD =10,E 是CD 上一点,若∠BAE =45°, DE =4,则BE = .(2)如图4,在平面直角坐标系xOy 中,点B 是x 轴上一 动点,且点A (3-,2),连结AB 和AO ,并以AB 为边向上作 正方形ABCD ,若C (x ,y ),试用含x 的代数式表示y , 则y = .已知:正方形ABCD 中,45MAN ∠=,绕点A 顺时针旋转,它的两边分别交CB 、DC (或它们的延长线)于点M 、N .(1)如图1,当MAN ∠绕点A 旋转到BM DN =时,有BM DN MN +=.当MAN ∠绕点A 旋转到BM DN ≠时,如图2,请问图1中的结论还是否成立?如果成立,请给予证明,如果不成立,请说明理由;(2)当MAN ∠绕点A 旋转到如图3的位置时,线段BM DN ,和MN 之间有怎样的等量关系?请写出你的猜想,并证明.24. 如图1,在等腰直角△ABC 中,∠BAC =90°,AB =AC =2,点E 是BC 边上一点,∠DEF =45°且角的两边分别与边AB ,射线CA 交于点P ,Q . (1)如图2,若点E 为BC 中点,将∠DEF 绕着点E 逆时针旋转,DE 与边AB 交于点P ,EF 与CA 的延长线交于点Q .设BP 为x ,CQ 为y ,试求y 与x 的函数关系式,并写出自变量x 的取值范围;CDOAB图4xy(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.海淀25.如图1,两个等腰直角三角板ABC和DEF有一条边在同一条直线l上,2DE=,1AB=.将直线EB绕点E逆时针旋转45︒,交直线AD于点M.将图1中的三角板ABC 沿直线l向右平移,设C、E两点间的距离为k.图1 图2 图3解答问题:(1)①当点C与点F重合时,如图2所示,可得AMDM的值为;②在平移过程中,AMDM的值为(用含k的代数式表示);(2)将图2中的三角板ABC绕点C逆时针旋转,原题中的其他条件保持不变.当点A落在线段DF上时,如图3所示,请补全图形,计算AMDM的值;(3)将图1中的三角板ABC绕点C逆时针旋转α度,0α<≤90,原题中的其他条件保持不变.计算AMDM的值(用含k的代数式表示).图1 图2 图3 图4昌平22. 阅读下面材料:小伟遇到这样一个问题:如图1,在正三角形ABC 内有一点P ,且P A =3 ,PB =4,PC =5,求∠APB 的度数.小伟是这样思考的:如图2,利用旋转和全等的知识构造△AP C ',连接PP ',得到两个特殊的三角形,从而将问题解决.PCBAABC PP 'D PACBABC DP FE请你回答:图1中∠APB 的度数等于 . 参考小伟同学思考问题的方法,解决下列问题:(1)如图3,在正方形ABCD 内有一点P ,且P A=PB =1,PD,则∠APB 的度数等于 ,正方形的边长为 ;(2)如图4,在正六边形ABCDEF 内有一点P ,且P A =2,PB =1,PFAPB 的度数等于 ,正六边形的边长为 .通州24.(9分)在平面直角坐标系xOy 中,点B (0,3),点C 是x 轴正半轴上一点,连结BC ,过点C 作直线CP ∥y 轴. (1)若含45°角的直角三角形如图所示放置.其中,一个顶点与点O 重合,直角顶点D在线段BC 上,另一个顶点E 在CP 上.求点C 的坐标; (2)若含30°角的直角三角形一个顶点与点O 重合,直角顶点D 在线段BC 上,另一个顶点E 在CP 上,求点C 的坐标.备用图备用图第24题图(西城19)如图所示,在平面直角坐标系xOy中,正方形PABC的边长为1,将其沿x轴的正方向连续滚动,即先以顶点A为旋转中心将正方形PABC顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为(,)x y.(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P的坐标;(2)画出点(,)P x y运动的曲线(0≤x≤4),并直接写出该曲线与x轴所围成区域的面积.东城24. 问题1:如图1,在等腰梯形ABCD中,AD∥BC,AB=BC=CD,点M,N分别在AD,CD上,若∠MBN=12∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;问题2:如图2,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD的延长线上,若∠MBN=12∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.昌平24.在△ABC中,AB=4,BC=6,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,连接AA1,CC1.若△CBC1的面积为3,求△ABA1的面积;(3)如图3,点E 为线段AB 中点,点P 是线段AC 上的动点,在△ABC 绕点B 按逆时针方向旋转的过程中,点P 的对应点是点P 1,直接写出线段EP 1长度的最大值与最小值.C 1C BA 1A图2A 1C 1ABC图1图3A朝阳24.在Rt △ABC 中,∠A =90°,D 、E 分别为AB 、AC 上的点.(1)如图1,CE =AB ,BD =AE ,过点C 作CF ∥EB ,且CF =EB ,连接DF 交EB 于点G ,连接BF ,请你直接写出EBDC 的值;(2)如图2,CE =kAB ,BD =kAE ,12EB DC =,求k 的值.西城24.在Rt △ABC 中,∠ACB =90°,∠ABC =α,点P 在△ABC 的内部.(1) 如图1,AB =2AC ,PB =3,点M 、N 分别在AB 、BC 边上,则cos α=_______, △PMN 周长的最小值为_______;(2) 如图2,若条件AB =2AC 不变,而P A =2,PB =10,PC =1,求△ABC 的面积; (3) 若P A =m ,PB =n ,PC =k ,且cos sin k m n αα==,直接写出∠APB 的度数.图2B 图1FB门头沟24.已知:在△ABC 中,AB =AC ,点D 为BC 边的中点,点F 是AB 边上一点,点E 在线段DF 的延长线上,点M 在线段DF 上,且∠BAE =∠BDF ,∠ABE =∠DBM . (1) 如图1,当∠ABC =45°时,线段 DM 与AE 之间的数量关系是 ; (2) 如图2,当∠ABC =60°时,线段 DM 与AE 之间的数量关系是 ;(3)① 如图3,当ABC α∠=(0<<90α︒︒)时,线段 DM 与AE 之间的数量关系是 ;② 在(2)的条件下延长BM 到P ,使MP =BM ,连结CP ,若AB =7,AE =27,求sin ∠ACP 的值.顺义24.如图1,将三角板放在正方形ABCD 上,使三角板的直角顶点E 与正方形ABCD 的顶点A 重合.三角板的一边交CD 于点F ,另一边交CB 的延长线于点.G (1)求证:EF EG =; (2)如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变, (1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由; (3)如图3,将(2)中的“正方形ABCD ”改为“矩形ABCD ”,且使三角板的一边经过点B ,其他条件不变,若AB a =,BC b =,求EFEG的值.A BCDEFM MFED CBA ABCD EF M 图1图2图3朝阳22.阅读下列材料:小华遇到这样一个问题,如图1, △ABC 中,∠ACB =30º,BC =6,AC =5,在△ABC 内部有一点P ,连接P A 、PB 、PC ,求P A +PB +PC 的最小值.小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC 绕点C 顺时针旋转60º,得到△EDC ,连接PD 、BE ,则BE 的长即为所求.(1)请你写出图2中,P A +PB +PC 的最小值为 ; (2)参考小华的思考问题的方法,解决下列问题:①如图3,菱形ABCD 中,∠ABC =60º,在菱形ABCD 内部有一点P ,请在图3中画出并指明长度等于P A +PB +PC 最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD 的边长为4,请直接写出当P A +PB +PC 值最小时PB 的长.丰台24.在Rt △ABC 中,AB =BC ,∠B =90°,将一块等腰直角三角板的直角顶点O 放在斜边AC 上,将三角板绕点O 旋转. (1)当点O 为AC 中点时,①如图1, 三角板的两直角边分别交AB ,BC 于E 、F 两点,连接EF ,猜想线段AE 、CF 与EF 之间存在的等量关系(无需证明);②如图2, 三角板的两直角边分别交AB ,BC 延长线于E 、F 两点,连接EF ,判断①中的猜想是否成立.若成立,请证明;若不成立,请说明理由;ECB图2B图3CB 图12)当点O 不是AC 中点时,如图3,,三角板的两直角边分别交AB ,BC 于E 、F 两点,若14AO AC=,求OE OF的值.朝阳期末25已知:在ABC ∆中︒=∠90ACB ,AB CD ⊥于点D ,点E 在AC 上,BE 交CD 于点G ,BE EF ⊥交AB 于点F 。