旋转中的半角模型视频讲义
- 格式:pdf
- 大小:299.32 KB
- 文档页数:2
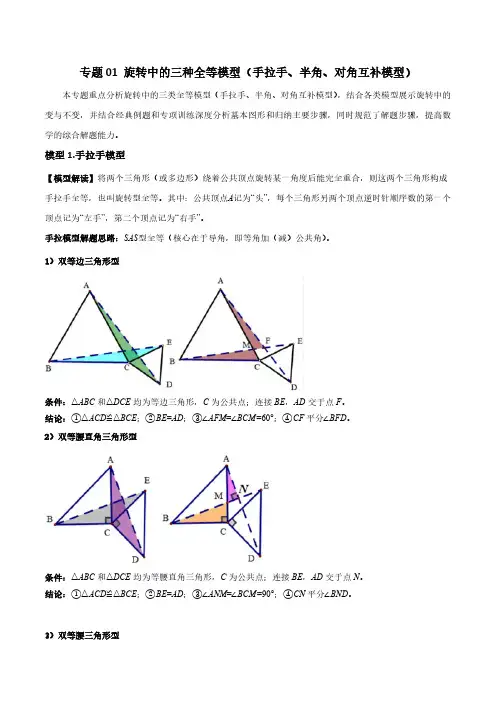
专题01 旋转中的三种全等模型(手拉手、半角、对角互补模型)本专题重点分析旋转中的三类全等模型(手拉手、半角、对角互补模型),结合各类模型展示旋转中的变与不变,并结合经典例题和专项训练深度分析基本图形和归纳主要步骤,同时规范了解题步骤,提高数学的综合解题能力。
模型1.手拉手模型【模型解读】将两个三角形(或多边形)绕着公共顶点旋转某一角度后能完全重合,则这两个三角形构成手拉手全等,也叫旋转型全等。
其中:公共顶点A记为“头”,每个三角形另两个顶点逆时针顺序数的第一个顶点记为“左手”,第二个顶点记为“右手”。
手拉模型解题思路:SAS型全等(核心在于导角,即等角加(减)公共角)。
1)双等边三角形型条件:△ABC和△DCE均为等边三角形,C为公共点;连接BE,AD交于点F。
结论:①△ACD≌△BCE;②BE=AD;③∠AFM=∠BCM=60°;④CF平分∠BFD。
2)双等腰直角三角形型条件:△ABC和△DCE均为等腰直角三角形,C为公共点;连接BE,AD交于点N。
结论:①△ACD≌△BCE;②BE=AD;③∠ANM=∠BCM=90°;④CN平分∠BND。
3)双等腰三角形型条件:△ABC 和△DCE 均为等腰三角形,C 为公共点;连接BE ,AD 交于点F 。
结论:①△ACD ≌△BCE ;②BE =AD ;③∠ACM =∠BFM ;④CF 平分∠AFD 。
4)双正方形形型条件:△ABCFD 和△CEFG 都是正方形,C 为公共点;连接BG ,ED 交于点N 。
结论:①△△BCG ≌△DCE ;②BG =DE ;③∠BCM =∠DNM=90°;④CN 平分∠BNE 。
例1.(2022·黑龙江·中考真题)ABC V 和ADE V 都是等边三角形.(1)将ADE V 绕点A 旋转到图①的位置时,连接BD ,CE 并延长相交于点P (点P 与点A 重合),有PA PB PC +=(或PA PC PB +=)成立;请证明.(2)将ADE V 绕点A 旋转到图②的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?并加以证明;(3)将ADE V 绕点A 旋转到图③的位置时,连接BD ,CE 相交于点P ,连接PA ,猜想线段PA 、PB 、PC 之间有怎样的数量关系?直接写出结论,不需要证明.【答案】(1)证明见解析 (2)图②结论:PB PA PC =+,证明见解析 (3)图③结论:PA PB PC+=【分析】(1)由△ABC 是等边三角形,得AB =AC ,再因为点P 与点A 重合,所以PB =AB ,PC =AC ,PA =0,即可得出结论;(2)在BP 上截取BF CP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明CAP BAF ≌△△(SAS ),得CAP BAF Ð=Ð,AF AP =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论;(3)在CP 上截取CF BP =,连接AF ,证明BAD CAE V V ≌(SAS ),得ABD ACE Ð=Ð,再证明BAP CAF ≌△△(SAS ),得出CAF BAP Ð=Ð,AP AF =,然后证明AFP V 是等边三角形,得PF AP =,即可得出结论:PA PB PF CF PC +=+=.(1)证明:∵△ABC 是等边三角形,∴AB =AC ,∵点P 与点A 重合,∴PB =AB ,PC =AC ,PA =0,∴PA PB PC +=或PA PC PB +=;(2)解:图②结论:PB PA PC=+证明:在BP 上截取BF CP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC CAD DAE CAD Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AC =AB ,CP =BF , ∴CAP BAF ≌△△(SAS ),∴CAP BAF Ð=Ð,AF AP =,∴CAP CAF BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PC PF BF PB +=+=;(3)解:图③结论:PA PB PC +=,理由:在CP 上截取CF BP =,连接AF ,∵ABC V 和ADE V 都是等边三角形,∴AB AC =,AD AE =,60BAC DAE Ð=Ð=°∴BAC BAE DAE BAE Ð+Ð=Ð+Ð,∴BAD CAE Ð=Ð,∴BAD CAE V V ≌(SAS ),∴ABD ACE Ð=Ð,∵AB =AC ,BP =CF ,∴BAP CAF ≌△△(SAS ),∴CAF BAP Ð=Ð,AP AF =,∴BAF BAP BAF CAF Ð+Ð=Ð+Ð,∴60FAP BAC Ð=Ð=°,∴AFP V 是等边三角形,∴PF AP =,∴PA PB PF CF PC +=+=,即PA PB PC +=.【点睛】本题考查等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键.例2.(2023·湖南·长沙市八年级阶段练习)如图1,在Rt △ABC 中,∠B =90°,AB =BC =4,点D ,E 分别为边AB ,BC 上的中点,且BD =BE .(1)如图2,将△BDE 绕点B 逆时针旋转任意角度α,连接AD ,EC ,则线段EC 与AD 的关系是 ;(2)如图3,DE ∥BC ,连接AE ,判断△EAC 的形状,并求出EC 的长;(3)继续旋转△BDE ,当∠AEC =90°时,请直接写出EC 的长.例3.(2023·黑龙江·虎林市九年级期末)已知Rt △ABC 中,AC =BC ,∠ACB =90°,F 为AB 边的中点,且DF =EF ,∠DFE =90°,D 是BC 上一个动点.如图1,当D 与C 重合时,易证:CD 2+DB 2=2DF 2;(1)当D 不与C 、B 重合时,如图2,CD 、DB 、DF 有怎样的数量关系,请直接写出你的猜想,不需证明.(2)当D 在BC 的延长线上时,如图3,CD 、DB 、DF 有怎样的数量关系,请写出你的猜想,并加以证明.【答案】(1)CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2,证明见解析【分析】(1)由已知得222DE DF =,连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论;(2)连接CF ,BE ,证明CDF BEF D @D 得CD =BE ,再证明BDE D 为直角三角形,由勾股定理可得结论.【详解】解:(1)CD 2+DB 2=2DF 2证明:∵DF =EF ,∠DFE =90°,∴222DF EF DE += ∴222DE DF = 连接CF ,BE ,如图∵△ABC 是等腰直角三角形,F 为斜边AB 的中点∴CF BF =,CF AB ^,即90CFB Ð=° ∴45FCB FBC Ð=Ð=°,90CFD DFB Ð+Ð=°又90DFB EFB Ð+Ð=° ∴CFD EFB Ð=Ð在CFD D 和BFE D 中CF BF CFD BFE DF EF =ìïÐ=Ðíï=î∴CFD D @BFED ∴CD BE =,45EBF FCB Ð=Ð=° ∴454590DBF EBF Ð+Ð=°+°=° ∴222DB BE DE +=∵CD BE =,222DE DF =∴CD 2+DB 2=2DF 2 ;(2)CD 2+DB 2=2DF 2 证明:连接CF 、BE∵CF =BF ,DF =EF 又∵∠DFC +∠CFE =∠EFB +∠CFB=90°∴∠DFC =∠EFB ∴△DFC ≌△EFB ∴CD =BE ,∠DCF =∠EBF =135°∵∠EBD =∠EBF -∠FBD =135°-45°=90° 在Rt △DBE 中,BE 2+DB 2=DE 2∵ DE 2=2DF 2 ∴ CD 2+DB 2=2DF 2【点睛】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、证明三角形全等是解决问题的关键,学会添加常用辅助线,构造全等三角形解决问题.例4.(2022·青海·中考真题)两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,把具有这个规律的图形称为“手拉手”图形.(1)问题发现:如图1,若ABC V 和ADE V 是顶角相等的等腰三角形,BC ,DE 分别是底边.求证:BD CE =;(2)解决问题:如图2,若ACB △和DCE V 均为等腰直角三角形,90ACB DCE Ð=Ð=°,点A ,D ,E 在同一条直线上,CM 为DCE V 中DE 边上的高,连接BE ,请判断∠AEB 的度数及线段CM ,AE ,BE 之间的数量关系并说明理由.图1 图2【答案】(1)见解析 (2)90DCE Ð=°;2AE AD DE BE CM=+=+【分析】(1)先判断出∠BAD =∠CAE ,进而利用SAS 判断出△BAD ≌△CAE ,即可得出结论;(2)同(1)的方法判断出△BAD ≌△CAE ,得出AD =BE ,∠ADC =∠BEC ,最后用角的差,即可得出结论.【解析】(1)证明:∵ABC V 和ADE V 是顶角相等的等腰三角形,∴AB AC =,AD AE =,BAC DAE Ð=Ð,∴BAC CAD DAE CAD Ð-Ð=Ð-Ð,∴BAD CAE Ð=Ð.在BAD V 和CAE V 中,AB AC BAD CAE AD AE =ìïÐ=Ðíï=î,∴()BAD CAE SAS ≌△△,∴BD CE =.(2)解:90AEB =°∠,2AE BE CM =+,理由如下:由(1)的方法得,≌ACD BCE V V ,∴AD BE =,ADC BEC ÐÐ=,∵CDE △是等腰直角三角形,∴45CDE CED Ð=Ð=°,∴180135ADC CDE Ð=°-Ð=°,∴135BEC ADC Ð=Ð=°,∴1354590AEB BEC CED Ð=Ð-Ð=°-°=°.∵CD CE =,CM DE ^,∴DM ME =.∵90DCE Ð=°,∴DM ME CM ==,∴2DE CM =.∴2AE AD DE BE CM =+=+.【点睛】此题是三角形综合题,主要考查了全等三角形的判定和性质,等腰三角形,等边三角形,等腰直角三角形的性质,判断出△ACD ≌△BCE 是解本题的关键.3)15°模型2.半角模型【模型解读】半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半思想方法:通过旋转构造全等三角形,实现线段的转化1)正方形半角模型条件:四边形ABCD是正方形,∠ECF=45°;结论:①△BCE≌△DCG;②△CEF≌△CGF;③EF=BE+DF;④D AEF的周长=2AB;⑤CE、CF分别平分∠BEF和∠EFD。


教材分析
本节课是鲁教版八年级上册第四章《图形的平移与旋转》的第二节课,本节立足于学生小学阶段学习基础和已有的生活经验,通过分析各种旋转现象的共性,直观地认识旋转,探索平面图形旋转的基本性质,利用旋转的基本性质进行简单的旋转画图,最后通过具体情境认识图形之间的变化关系。
具体分为三个课时:第一课时认识平面图形的旋转,探索旋转的基本性质;第二课时主要研究旋转画图;第三课时通过具体情境认识图形之间的变换关系。
《图形的旋转》这部分知识在其他版本教材中分别是人教版九年级上册第二十三章;北师大版八年级下册第三章第二节,这两个版本的教材内容主要研究旋转的定义,旋转的性质及其应用。
这几个版本的教材都是在学生学习了平移和轴对称基础上学习的,对发展学生的空间观念是一个渗透,是后续学习中心对称图形及其图形变化的基础,是空间与图形领域的基础知识,在教材中,起着承上启下的作用,同时,旋转在日常生活中的应用也非常广泛,利用旋转可以帮助我们解决很多实际问题。

旋转模型-角含半角模型【内容介绍】本次资料主要包含数学科目,重点指导学生了解旋转模型相关知识,掌握不同旋转模型的解题方法;主要是通过要点梳理,帮助大家综合掌握角含半角模型的含义和解题方法,再通过典型例题的分析,帮助大家了解常考题型。
建议大家深入学习掌握要点梳理,认真研读例题,并在日常学习中注重练习,实现对学习目标的综合把握。
【要点梳理】1)半角模型概念:过多边形一个顶点作两条射线,使这两条射线夹角等于该顶角一半2)思想方法:通过旋转构造全等三角形,实现线段的转化3)基本模型要点一、正方形含半角图1 图2△△△△AEF AEB AFDS S +S )4(;BEF 分平 EA ,DFE 分平 FA )3(;半一的长周形方正是长周的(2) CEF EF=BE+DF;)1(:论结的下以明证,EAF=45,点的上边CD 、BC 是别分F 、E ,中ABCD 形方正在:1图如:题例=∠∠∠︒。
化转的角和段线现实,形角三等全造构转旋过通,型模角半合符,角45有含中角90:析分︒︒△△△△△△△△△AEG AEF AEG AEF G AFE AFD CEF BE BG BE DF AEF AEG AEB AEG AEB AFD 证得S S =S S S S ;证得;证得EF+CE+CF=BE+CE+DF+CF=BC+CD,(2)长周的。
立成=+=+≅∴∠=∠∠=∠=∠∴∴+=+,(4),,,(3)=(1),△△△△△EF EG AEG AEF AE AE AEG AEF EAG EAF AG AF EAG EAF EAF G B C GBC ABG ABC ABG AG AF ABG D BG DF ABCD AD AB ,,中和在,,线共点三、、则,到得,转旋针时顺点沿将,中形方正在,图如:答解∴==∴≅⎩=⎪⎨∠∠⎪⎧=∴∠∠︒∠︒∴∴∠∠+∠︒∠︒∆=∠=∠=︒=∠=︒=︒,===45=45==180ABC =90,90,,GAF 90,2,ADF A 90。

旋转中的几何模型模型一角含半角模型模型特征:角含半角模型,顾名思义即一个角包含着它的一半大小的角。
它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。
解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。
1综合与实践:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF= 45°,连接EF,求证:DE+BF=EF.李伟同学是这样解决的:将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,再证明△GAF≌△EAF,可得结论.(1)如图2,在四边形ABCD中,AD∥BC AD>BC,∠D=90°,AD=CD=10,且∠BAE= 45°,DE=4,求BE的长;(2)类比(1)证明思想完成下列问题:在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),在旋转过程中,等式BD2+CE2=DE2始终成立,请说明理由.2如图,△ABC中,AB=AC,∠BAC=90°,点D、E在BC边上,∠DAE=45°,将△ACE绕点A顺时针旋转90°得△ABF.(1)求证:BF⊥BC;(2)连接DF,求证:△ADF≌△ADE;(3)若BD=3,CE=4,则DF=,四边形AFDE的面积=.针对训练13如图,在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=45°,分别连接EF、BD,BD与AF、AE分别相交于点M、N(1)求证:EF=BE+DF为了证明“EF=BE+DF”,小明延长CB至点G,使BG=DF,连接AG,请画出辅助线并按小明的思路写出证明过程.(2)若BE=2,DF=3,请求出正方形ABCD的边长.(3)请直接写出线段BN、MN、DM三者之间的数量关系4如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?(3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题:①如图2,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=6,E是AB的中点,且∠DCE=45°,求DE的长;②如图3,在△ABC中,∠BAC=45°,AD⊥BC,BD=4,CD=6,则△ABC的面积为(直接写出结果,不需要写出计算过程).拓展类型 构造旋转模型解题方法指导:若一个图形中含有相等的线段和特殊的角度,通常是以等线段的公共端点为旋转中心进行旋转,使得相等的边重合,得出特殊的图形.1请阅读下列材料:问题:如图1,在等边△ABC内有一点P,且PA=2,PB=3,PC=1,求∠BPC的度数和等边△ABC的边长.李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),所以∠BPC =∠AP′B=150°,进而求出等边△ABC的边长为7,问题得到解决.请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA= 5,BP=2,PC=1.求∠BPC的度数和正方形ABCD的边长.2如图1,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.(1)求证:EB=GD且EB⊥GD;(2)若AB=2,AG=2,求BE的长;针对训练25以△ABC的AB、AC为边作△ABD和△ACE,且AE=AB,AC=AD,CE与BD相交于M,∠EAB=∠CAD=α.(1)如图1,若α=40°,求∠EMB的度数;(2)如图2,若G、H分别是EC、BD的中点,求∠AHG的度数(用含α式子表示);(3)如图3,连接AM,直接写出∠AMC与α的数量关系是.6在△ABC中,∠BAC=90°,AC=AB,点D为直线BC上的一动点,以AD为边作△ADE (顶点A、D、E按逆时针方向排列),且∠DAE=90°,AD=AE,连接CE.(1)如图1,若点D在BC边上(点D与B、C不重合),①求证:△ABD≌△ACE;②求证:DE2=BD2+CD2(2)如图2,若点D在CB的延长线上,若DB=5,BC=7,则△ADE的面积为.(3)如图3,若点D在BC的延长线上,以AD为边作等腰Rt△ADE,∠DAE=90°,连结BE,若BE=10,BC=6,则AE的长为.巩固练习1已知在△ABC中,BC=4。




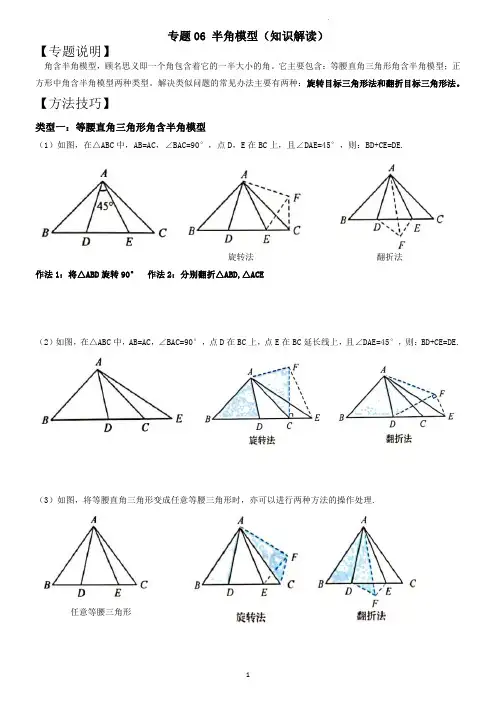
专题06半角模型(知识解读)【专题说明】角含半角模型,顾名思义即一个角包含着它的一半大小的角。
它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。
解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。
【方法技巧】类型一:等腰直角三角形角含半角模型(1)如图,在△ABC中,AB=AC,∠BAC=90°,点D,E在BC上,且∠DAE=45°,则:BD+CE=DE.旋转法翻折法作法1:将△ABD旋转90°作法2:分别翻折△ABD,△ACE(2)如图,在△ABC中,AB=AC,∠BAC=90°,点D在BC上,点E在BC延长线上,且∠DAE=45°,则:BD+CE=DE.(3)如图,将等腰直角三角形变成任意等腰三角形时,亦可以进行两种方法的操作处理.任意等腰三角形类型二:正方形中角含半角模型(1)如图,在正方形ABCD 中,点E,F 分别在边BC,CD 上,∠EAF=45°,连接EF,过点A 作AG⊥于EF 于点G,则:EF=BE+DF,AG=AD.图示(1)作法:将△ABE 绕点A 逆时针旋转90°(2)如图,在正方形ABCD 中,点E,F 分别在边CB,DC 的延长线上,∠EAF=45°,连接EF,则:EF=DF-BE.图示(2)作法:将△ABE 绕点A 逆时针旋转90°(3)如图,将正方形变成一组邻边相等,对角互补的四边形,在四方形ABCD 中,AB=AD,∠BAD+∠C=180°,点E,F 分别在边BC,CD 上,∠EAF=21∠BAD,连接EF,则:EF=BE+DF.图示(3)作法:将△ABE 绕点A 逆时针旋转∠BAD 的大小类型三:等边三角形中120°含60°的半角模型作辅助线:延长FC到G,使得CG=BE,连接DG结论:▲DEF≌▲DGF;EF=BE+CF【类型一:等腰直角三角形角含半角模型】【典例1】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,若将△ABC绕着点C逆时针旋转90°得△EDC.(1)求证:∠ADC+∠CDE=180°;(2)若AB=3cm,AC=,求AD的长;(3)在(2)的条件下,求四边形ABCD的周长和面积.【变式1-1】如图,Rt△ABC中,∠BAC=90°,AB=AC,D、E为BC边上两点,∠DAE=45°,过A点作AF⊥AE,且AF=AE,连接DF、BF.下列结论:①△ABF≌△ACE,②AD平分∠EDF;③若BD=4,CE=3,则AB=6;④若AB=BE,S△ABD=,其中正确的个数有()A.1个B.2个C.3个D.4个【变式1-2】如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM =1,CN=3,则MN的长为.【类型二:正方形中角含半角模型】【典例2】(2022春•西山区校级月考)如图,已知正方形ABCD,点E、F分别是AB、BC边上,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:△EDF≌△MDF;(2)若正方形ABCD的边长为5,AE=2时,求EF的长?【变式2-1】(2022春•路北区期末)如图,在边长为6的正方形ABCD内作∠EAF=45°,AE交BC于点E,AF 交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG.(1)求证:GE=FE;(2)若DF=3,求BE的长为.【变式2-2】(2021秋•山西期末)阅读以下材料,并按要求完成相应的任务:从正方形的一个顶点引出夹角为45°的两条射线,并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型.半角模型可证出多个几何结论,例如:如图1,在正方形ABCD中,以A为顶点的∠EAF=45°,AE、AF与BC、CD边分别交于E、F两点.易证得EF =BE+FD.大致证明思路:如图2,将△ADF绕点A顺时针旋转90°,得到△ABH,由∠HBE=180°可得H、B、E三点共线,∠HAE=∠EAF=45°,进而可证明△AEH≌△AEF,故EF=BE+DF.任务:如图3,在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BAD=120°,以A为顶点的∠EAF=60°,AE、AF与BC、CD边分别交于E、F两点.请参照阅读材料中的解题方法,你认为结论EF=BE+DF是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.【典例3】已知正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N,AH⊥MN于点H.(1)如图①,当∠MAN绕点A旋转到BM=DN时,请你直接写出AH与AB的数量关系:;(2)如图②,当∠MAN绕点A旋转到BM≠DN时,(1)中发现的AH与AB的数量关系还成立吗?如果不成立请写出理由,如果成立请证明;(3)如图③,已知∠MAN=45°,AH⊥MN于点H,且MH=2,AH=6,求NH的长.(可利用(2)得到的结论)【变式3-1】探究:(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果:;(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明.【变式3-2】已知:如图边长为2的正方形ABCD中,∠MAN的两边分别交BC、CD边于M、N两点,且∠MAN=45°①求证:MN=BM+DN;②若AM、AN交对角线BD于E、F两点.设BF=y,DE=x,求y与x的函数关系式.【类型三:等边三角形中120°含60°的半角模型】【典例4】已知在△ABC中,AB=AC,D,E是BC边上的点,将△ABD绕点A旋转,得到△ACD',连接D'E.(Ⅰ)如图1,当∠BAC=120°,∠DAE=60°时,求证:DE=D'E;(Ⅱ)如图2,当DE=D'E时,请写出∠DAE与∠BAC的数量关系,并说明理由.(Ⅲ)当∠BAC=90°,DE=D'E,EC=CD'时,请直接写出BD与DE的数量关系(不必说明理由).【变式4-1】(2017秋•锦江区期末)在△ABC中,AB=AC,点E,F是边BC所在直线上与点B,C不重合的两点.(1)如图1,当∠BAC=90°,∠EAF=45°时,直接写出线段BE,CF,EF的数量关系;(不必证明)(2)如图2,当∠BAC=60°,∠EAF=30°时,已知BE=3,CF=5,求线段EF的长度;(3)如图3,当∠BAC=90°,∠EAF=135°时,请探究线段CE,BF,EF的数量关系,并证明.【变式4-2】等边△ABC,D为△ABC外一点,∠BDC=120°,BD=DC,∠MDN=60°,射线DM与直线AB相交于点M,射线DN与直线AC相交于点N,①当点M、N在边AB、AC上,且DM=DN时,直接写出BM、NC、MN之间的数量关系.②当点M、N在边AB、AC上,且DM≠DN时,猜想①中的结论还成立吗?若成立,请证明.③当点M、N在边AB、CA的延长线上时,请画出图形,并写出BM、NC、MN之间的数量关系.。

中考数学几何模型5 :角含半角模型TH名师点睛角含半角模型,顾名思义即一个角包含着它的一半大小的角。
它主要包含:等腰直角三角形角含半角 模型;正方形中角含半角模型两种类型。
解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折 目标三角形法。
类型一:等腰直角三角形角含半角模型(1) 如图,在厶ABC 中,AB=AC ,/ BAC=90 ° ,点 D , E 在 BC 上, 且/ DAE=45 ° ,贝U: BD 2+CE 2=DE 2(3)如图,将等腰直角三角形变成任意等腰三角形时,亦可以进行两种方法的操作处理图示(1)作法1:将厶ABD 旋转90° 作法2:分别翻折厶ABD, △ ACE(2)如图,在△ ABC 中,AB=AC ,/ BAC=90 ,点D 在BC 上,点E 在BC 延长线上,且/ DAE=45贝y : BD 2+CE 2=DE 2. 图示(2)旋转扶 翱折旅拨开云雾开门见山类型二:正方形中角含半角模型(1) 如图,在正方形 ABCD 中,点E, F 分别在边BC , CD 上,/ EAF=45 °,连接EF ,过点A 作AG 丄 于 EF 于点 G,则:EF=BE+DF , AG=AD.图示(2) 作法:将厶ABE 绕点A 逆时针旋转90°(3)如图,将正方形变成一组邻边相等,对角互补的四边形,在四方形ABCD 中,AB=AD ,/ BAD+ /1C=180。
,点 E, F 分别在边 BC, CD 上,/ EAF= / BAD ,连接 EF ,则:EF=BE+DF.2(2) 如图,在正方形ABCD 中,点E,F 分别在边 CB , DC 的延长线上,/ EAF=45,连接 EF,则:EF=DF-BE.图示(3)作法:将厶ABE绕点A逆时针旋转/ BAD的大小典题探究 ----------------------------------------------------------------例题1.如图,正方形 ABCD 的边长为4,点E, F 分别在AB, AD 上,若CE = 5,且/ ECF = 45°,贝U CF【解答】解:如图,延长 FD 到G,使DG = BE;连接CG 、EF ;CCB=CD•••四边形 ABCD 为正方形,在△ BCE 与厶 DCG 中,{/,「•△ BCE ◎△ DCG ( SAS),I BE =DG••• CG = CE,/ DCG = Z BCE ,.・./ GCF = 45°,GC=ICZGCF=ZECF ,^^ GCF ◎△ ECF ( SAS ), • GF = EF , CF=CF•/ CE= 5, CB = 4,「. BE= 3, • AE = 1,设 AF = x,贝V DF = 4 - x, GF = 1+ (4 - x)= 5 - x,「. EF =寸扎g? +/=〈]+J , •••( 5- x) 2= 1+x 2,「. x=―,即 AF =—,••• DF = 4-—丄,__________ 555 5• CF = J :千】=4 I( _: =4_<l ,故答案为:4. i.变式练习>>> AB = BC+AD , / DAC = 45°, E 为 CD 上一点,且/ )•/ AD // BC,[启迪思维探究重点1.如图四边形BAE = 45 ° ABCD 中,AD // BC ,/ BCD = 90°.若CD = 4,则厶ABE 的面积为(B .晋【解答】解法一:作 AF 丄CB 交CB 的延长线于C.5048 F ,在CF 的延长线上取一点 G ,使得FG = DE .•••/ BCD+ / ADC = 180°,•••/ ADC = / BCD =/ AFC = 90°,•四边形ADCF是矩形,•// CAD = 45••• AD = CD,•••四边形ADCF是正方形,•AF = AD,/ AFG =Z ADF = 90°,•△ AFG ◎△ ADE,•AG = AE,/ FAG=Z DAE ,•••/ FAG+ / FAB = / EAD + / FAB= 45 ° =/ BAE, •△ BAE◎△ BAG ,BE= BG= BF+GF = BF+DE ,设 BC = a,则 AB= 4+a, BF = 4 - a,在 Rt△ ABF 中,42+ (4- a) 2=( 4+a) 2,解得 a = 1, BC= 1, BF = 3,设 BE= b,贝U DE = b - 3, CE= 4 -在Rt△ BCE 中,12+ (7 - b) 2(b-3)= 7- b.=b2,解得 b= —BG = BE = 251x25x 4= 50~77例题2.在正方形 ABCD中,连接BD .(1)如图1 , AE丄BD于E.直接写出/ BAE的度数.(2)如图1,在(1 )的条件下,AB'与BD交于M , AE '的延长线与 BD交于N .①依题意补全图1;②用等式表示线段 BM、DN和MN之间的数量关系,并证明.(3)如图2, E、F是边BC、CD上的点,△ CEF周长是正方形交于M、N,写出判断线段 BM、DN、MN之间数量关系的思路. ABCD周长的一半, AE、AF分另U与 BD (不必写出完整推理过程)【解答】解:(1)v BD是正方形ABCD的对角线,•••/ ABD = / ADB = 45°,•/ AE丄 BD,ABE = / BAE = 45°,(2)①依题意补全图形,如图 1所示,②BM、DN和MN之间的数量关系是 BM2+MD2= MN2, 将厶AND 绕点D顺时针旋转 90°,得到△ AFB,ADB = / FBA , / BAF = / DAN , DN = BF , AF = AN , •••在正方形 ABCD中,AE丄BD ,ADB = / ABD = 45°,FBM =/ FBA+ / ABD = / ADB+ /ABD = 90°,在Rt△ BFM中,根据勾股定理得,FB2+BM2= FM2, •••旋转△ ANE 得到 AB1E1,• S A ABE = S A ABG =⑶如團2,A 顺时针濮转得到心EG ,:、D2GE 、•「正方形肋CD 的周长肓4AD△CEF 周长为 EF-ECY 。