下载文档原格式
多因素方差分析多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS调用“Univariate”过程，检验不同水平组合之间因变量均数，由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用，也可以分析因素之间的交互作用，以及分析协方差，以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来，且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量，协变量与因变量不彼此独立。
因素变量是分类变量，可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。
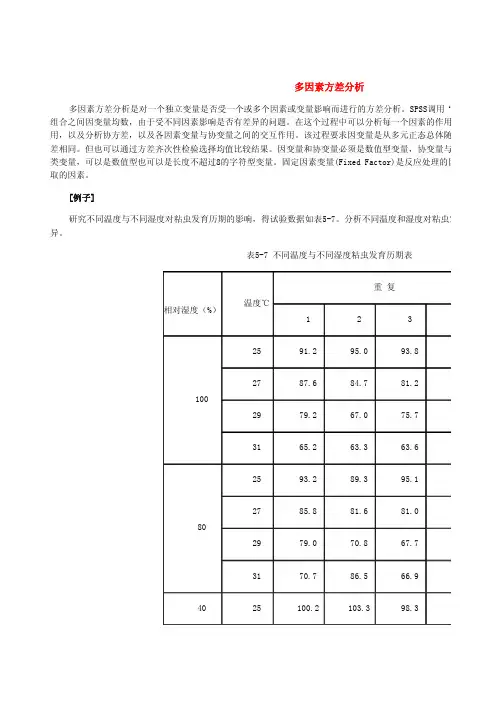
[例子]研究不同温度与不同湿度对粘虫发育历期的影响，得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
表5-7 不同温度与不同湿度粘虫发育历期表数据保存在“DATA5-2.SAV”文件中，变量格式如图5-1。
1）准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量，因素变量温度“A”，湿度为“B”变量，重复变量“重复”。
然后输入对应的数值，如图5-6所示。
或者打开已存在的数据文件“DATA5-2.SAV”。
图5-6 数据输入格式2）启动分析过程点击主菜单“Analyze”项，在下拉菜单中点击“General Linear Model”项，在右拉式菜单中点击“Univariate”项，系统打开单因变量多因素方差分析设置窗口如图5-7。
图5-7 多因素方差分析窗口3）设置分析变量设置因变量:在左边变量列表中选“历期”，用向右拉按钮选入到“Dependent Variable：”框中。
设置因素变量:在左边变量列表中选“a”和“b”变量，用向右拉按钮移到“Fixed Factor(s):”框中。
可以选择多个因素变量。
多因素方差分析多因素方差分析是对一个独立变量是否受一个或多个因素或变量影响而进行的方差分析。
SPSS调用“Univariate”过程，检验不同水平组合之间因变量均数，由于受不同因素影响是否有差异的问题。
在这个过程中可以分析每一个因素的作用，也可以分析因素之间的交互作用，以及分析协方差，以及各因素变量与协变量之间的交互作用。
该过程要求因变量是从多元正态总体随机采样得来，且总体中各单元的方差相同。
但也可以通过方差齐次性检验选择均值比较结果。
因变量和协变量必须是数值型变量，协变量与因变量不彼此独立。
因素变量是分类变量，可以是数值型也可以是长度不超过8的字符型变量。
固定因素变量(Fixed Factor)是反应处理的因素;随机因素是随机地从总体中抽取的因素。
[例子]研究不同温度与不同湿度对粘虫发育历期的影响，得试验数据如表5-7。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
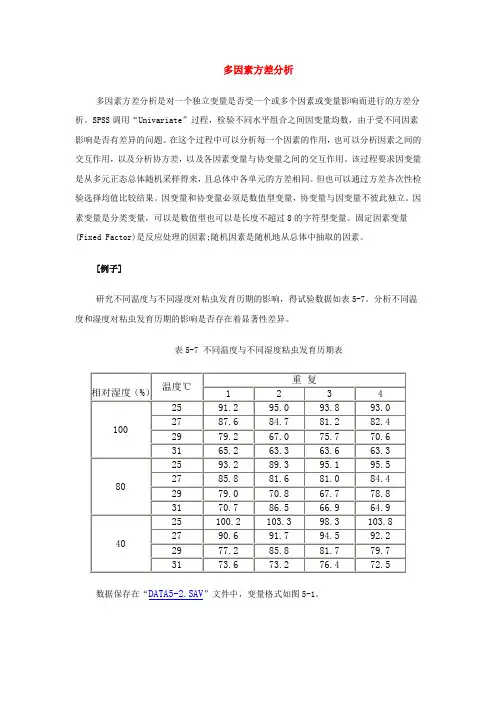
表5-7 不同温度与不同湿度粘虫发育历期表表5-7 不同温度与不同湿度粘虫发育历期表相对湿度（%）温度℃重复1 2 3 4100 25 91.2 95.0 93.8 93.027 87.6 84.7 81.2 82.429 79.2 67.0 75.7 70.631 65.2 63.3 63.6 63.380 25 93.2 89.3 95.1 95.527 85.8 81.6 81.0 84.429 79.0 70.8 67.7 78.831 70.7 86.5 66.9 64.940 25 100.2 103.3 98.3 103.827 90.6 91.7 94.5 92.229 77.2 85.8 81.7 79.731 73.6 73.2 76.4 72.51）准备分析数据在数据编辑窗口中输入数据。
建立因变量历期“历期”变量，因素变量温度“A”，湿度为“B”变量，重复变量“重复”。
然后输入对应的数值，如图5-6所示。
多因素方差分析结果解读多因素方差分析是一种统计学方法，用于衡量研究变量之间的统计关系，以了解不同变量之间的交互作用。
多因素方差分析(ANOVA)可以使科学家、工程师和其他研究者探索并发现不同因素（变量）之间的关系，以便对有效的解释和可视化的信息进行解读。
本文将讨论多因素方差分析结果解读的基本概念，以及基于多因素方差分析数据分析结果正确解读的重要性。
首先，需要了解多因素方差分析的基本知识和步骤。
“多因素方差分析”是一种在统计学中用来确定多个变量之间关系的统计方法。
它可以在每个变量之间检测不同水平的均方差，以了解变量之间的交互作用。
这种分析通过定义变量并应用严格的统计标准来识别和分析变量之间的关系。
多因素方差分析的结果解释是有价值的，因为它们可以帮助研究者了解不同变量之间的关系，从而推断其中的交互作用。
多因素方差分析结果的正确解读可以帮助科学家和其他研究者更好地了解和探究变量之间的关系，以便建立准确有效的模型。
进行多因素方差分析时，最重要的是执行正确的统计分析，以便对数据进行准确描述。
多因素方差分析结果解释也是一种重要的工具，可以帮助研究者确定变量之间的关系，从而建立有效的模型。
正确的解释需要考虑变量之间的相关性，以及它如何影响整个分析的结果。
多因素方差分析的结果可以很好地说明变量之间的关系。
研究者可以根据结果检查各个变量之间的相关性，以及每个变量如何影响研究结果。
多因素方差分析结果解释可以帮助研究者更好地识别和分析变量之间的关系，从而建立有效的模型。
多因素方差分析结果解释的重要性在于它可以帮助研究者更加准确地了解研究问题，并对不同变量之间的相互作用做出准确的推断。
多因素方差分析的结果可以帮助研究者了解具体的研究内容，从而更好地回答研究问题。
总之，多因素方差分析结果解释在研究变量之间关系的统计学中十分重要，可以帮助研究者更加准确地了解研究变量之间的关系，并对不同变量之间的相互作用做出准确的推断。
正确理解和使用多因素方差分析结果解释，可以帮助研究者更好地利用和分析其研究结果，从而产生更有效的解决方案。
