下载文档原格式
机械原理课后答案第2章第2章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答：参考教材5~7页。
2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答：机构运动简图可以表示机构的组成和运动传递情况，可进行运动分析，而且也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时，机构的运动将发生什么情况?答：参考教材12~13页。
2-4 何谓最小阻力定律?试举出在机械工程中应用最小阻力定律的1、2个实例。
2-5 在计算平面机构的自由度时，应注意哪些事项? 答：参考教材15~17页。
2-6 在图2-20所示的机构中，在铰链C、B、D处，被连接的两构件上连接点的轨迹都是重合的，那么能说该机构有三个虚约束吗?为什么?答：不能，因为在铰链C、B、D中任何一处，被连接的两构件上连接点的轨迹重合是由于其他两处的作用，所以只能算一处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答：参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答：参考教材20~21页。
2-9 任选三个你身边已有的或能观察到的下列常用装解：342511f=⨯-⨯-=A为复合铰链（b）解：（1）图示机构在D处的结构与图2-1所示者一致，经分析知该机构共有7个活动构件，8个低副(注意移动副F与F’，E与E’均只算作一个移动副)，2个高副；因有两个滚子2、4，所以有两个局部自由度，没有虚约束，故机构的自由度为F=3n- (2p l+p h- p’)- F’=3ⅹ7- (2ⅹ8+2-0)- 2=1 （2）如将D处结构改为如图b所示形式，即仅由两个移动副组成。
注意，此时在该处将带来一个虚约束。
因为构件3、6和构件5、6均组成移动副，均要限制构件6在图纸平面内转动，这两者是重复的，故其中有一个为虚约束。
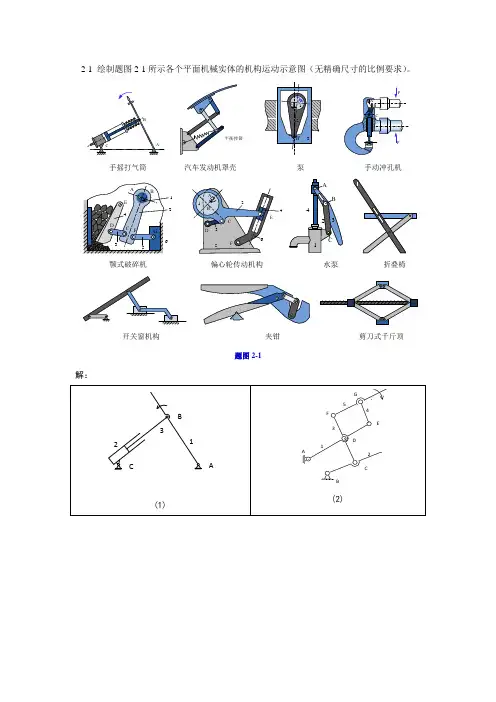
2-1 绘制题图2-1所示各个平面机械实体的机构运动示意图（无精确尺寸的比例要求）。
手摇打气筒汽车发动机罩壳泵手动冲孔机1颚式破碎机偏心轮传动机构水泵折叠椅开关窗机构夹钳剪刀式千斤顶题图2-1解：2-4 在题图2-4所示的铰链四杆机构中，已知l AB =50mm ，l BO 1=35mm ，l O 1O 3 =30mm ，取O 1O 3为机架。
（1） 如果该机构能成为曲柄摇杆机构，且O 1A 是曲柄，求l AO 1的取值范围； （2） 如果该机构能成为双曲柄机构，求l AO 1的取值范围； （3） 如果该机构能成为双摇杆机构，求l AO 1的取值范围。
AB1O 3O题图2-4答：(1) l AO115mm(2) 45mm l AO155mm(3) 15mm< l AO1<45mm 或55< l AO1<1152-5 在题图2-5所示的铰链四杆机构中，各杆件长度分别为l AB =28mm ，l BC =70mm ，l CD =50mm ，l AD =72mm 。
若取AB 为机架，该机构将演化为何种类型的机构为什么请说明这时C 、D 两个转动副是周转副还是摆转副ABC题图2-5答：由于28+72 < 70+50，因此存在曲柄，又因为AB 为最短杆，故若取AB 为机架，该机构将演化为为双曲柄机构。
这时C 、D 均为摆转副。
2-6 试推导有无偏置条件下，曲柄滑块机构中的曲柄存在条件。
已知曲柄长为a ，连杆长为b ，偏置为e 。
答：无偏置时，曲柄存在的条件是ab ；有偏置时，曲柄存在的条件是a +eb 。
例2-10 在例2-10图所示中，已知各构件的尺寸及机构的位置，各转动副处的摩擦圆如图中虚线圆，移动副及凸轮高副处的摩擦角为ϕ，凸轮顺时针转动，作用在构件4上的工作阻力为Q 。
试求该图示位置：1． 各运动副的反力（各构件的重力和惯性力均忽略不计）； 2． 需施加于凸轮1上的驱动力矩1M ； 3． 机构在图示位置的机械效率η。
例2-10解题要点：考虑摩擦时进行机构力的分析，关键是确定运动副中总反力的方向。
为了确定总反力的方向，应先分析各运动副元素之间的相对运动，并标出它们相对运动的方向；然后再进行各构件的受力分析，先从二力构件开始，在分析三力构件。
解：选取长度比例尺l μ(m/mm)作机构运动简图。
1． 确定各运动副中总反力的方向。
如例2-10(a)图，根据机构的运动情况和力的平衡条件，先确定凸轮高副处的总反力12R 的方向，该力方向与接触点B 处的相对速度21B B v 的方向成090ϕ+角。
再由51R 应切于运动副A 处的摩擦圆，且对A 之矩的方向与1ω方向相反，同时与12R 组成一力偶与1M 平衡，由此定出51R 的方向；由于连杆3为二力构件，其在D ，E 两转动副受两力23R 及43R 应切于该两处摩擦圆，且大小相等方向相反并共线，可确定出23R 及43R 的作用线，也即已知32R 及34R 的方向线；总反力52R ，应切于运动副C 处的摩擦圆，且对C 之矩的方向应与25ω方向相反，同时构件2受到12R ，52R 及32R 三个力，且应汇交于一点，由此可确定出52R 的方向线；滑块4所受总反力54R 应与45v 的方向成090ϕ+角，同时又受到34R ，54R 及Q 三个力，也应汇交于一点，由此可确定出54R 的方向线。
2． 求各运动副中总反力的大小。
分别取构件2，4为分离体，列出力平衡方程式 构件2 1232520R R R ++= 构件434540R R Q ++=而34432332R R R R =-==-根据上述3个力平衡方程式，选取力比例尺F μ(N/mm)，并作力多边形如例2-10(b)图所示。
第2章连杆机构分析和设计2.1内容要求1.掌握平面四杆机构的基本型式、特点及其演化方法。
2.熟练掌握和推导铰链四杆机构曲柄存在条件，并灵活运用来判断铰链四杆机构的类型；掌握曲柄滑块机构及导杆机构等其他四杆机构的曲柄存在条件的推导过程。
3.掌握平面四杆机构的压力角、传动角、急回运动、极位夹角、行程速比系数、等基本概念；掌握连杆机构最小传动角出现的位置及计算方法；掌握极位夹角与行程速比系数的关系式；掌握掌握死点在什么情况下出现及死点位置在机构中的应用。
4.掌握速度瞬心的概念及如何确定机构中速度瞬心的数目；掌握“三心定理”并应用“三心定理”确定机构中速度瞬心的位置及对机构进行速度分析。
5.了解建立Ⅰ级机构、RRR杆组、RRP杆组、RPR杆组、PRP杆组、RPP杆组的运动分析数学模型；掌握相对运动图解法及杆组法机构运动分析的方法。
6.掌握移动副、转动副中摩擦力的计算和自锁问题的讨论；掌握计及摩擦时平面连杆机构受力分析的方法；掌握计算机械效率的几种方法；掌握从机械效率的观点研究机械自锁条件的方法和思想。
7.掌握平面四杆机构的运动特征及其设计的基本问题；了解“函数机构”、“轨迹机构”、“导引机构”的设计思想、方法；掌握按给定行程速比系数设计四杆机构的方法。
2.2内容提要一、本章重点本章重点是铰链四杆机构曲柄存在条件，并灵活运用来判断铰链四杆机构的类型；连杆机构最小传动角出现的位置及计算方法；速度瞬心法对机构进行速度分析；计及摩擦时平面连杆机构受力分析的方法；按给定行程速比系数设计四杆机构的方法。
1．平面四杆机构的基本型式及其演化型式平面四杆机构的基本型式是平面铰链四杆机构。
在此机构中，与机架相联的构件称为连架杆；能作整周回转的连架杆称为曲柄，而不能作整周回转的连架杆称为摇杆；与机架不相连的中间构件称为连杆。
能使两构件作整周相对转动的转动副称为周转副；而不能作整周相对转动的转动副称为摆转副。
平面铰链四杆机构又根据两连架杆运动形式不同分为曲柄摇杆机构、双曲柄机构及双摇杆机构。
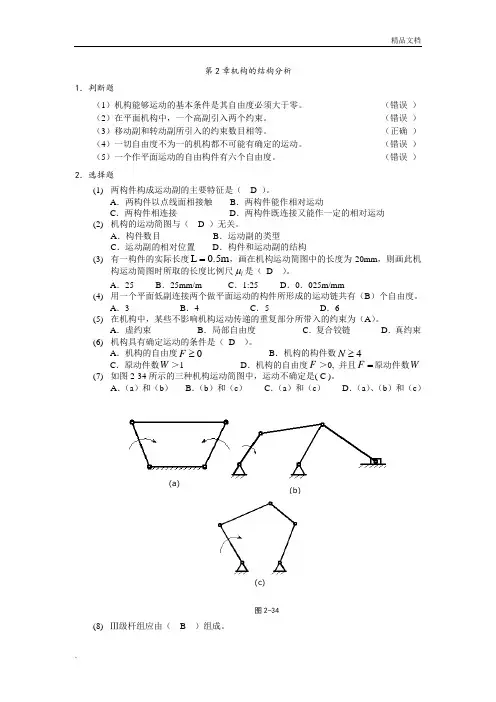
第2章机构的结构分析1．判断题（1）机构能够运动的基本条件是其自由度必须大于零。
（错误 ）（2）在平面机构中，一个高副引入两个约束。
（错误 ）（3）移动副和转动副所引入的约束数目相等。
（正确 ）（4）一切自由度不为一的机构都不可能有确定的运动。
（错误 ）（5）一个作平面运动的自由构件有六个自由度。
（错误 ）2．选择题(1) 两构件构成运动副的主要特征是（ D ）。
A ．两构件以点线面相接触B ．两构件能作相对运动C ．两构件相连接D ．两构件既连接又能作一定的相对运动(2) 机构的运动简图与（ D ）无关。
A ．构件数目B ．运动副的类型C ．运动副的相对位置D ．构件和运动副的结构(3) 有一构件的实际长度0.5m L =，画在机构运动简图中的长度为20mm ，则画此机构运动简图时所取的长度比例尺l μ是（ D ）。
A ．25B ．25mm/mC ．1:25D ．0．025m/mm(4) 用一个平面低副连接两个做平面运动的构件所形成的运动链共有（B ）个自由度。
A ．3B ．4C ．5D ．6(5) 在机构中，某些不影响机构运动传递的重复部分所带入的约束为（A ）。
A ．虚约束B ．局部自由度C ．复合铰链D ．真约束(6) 机构具有确定运动的条件是（ D ）。
A ．机构的自由度0≥FB ．机构的构件数4≥NC ．原动件数W ＞1D ．机构的自由度F ＞0, 并且=F 原动件数W(7) 如图2-34所示的三种机构运动简图中，运动不确定是( C )。
A ．（a ）和（b ）B ．（b ）和（c ）C ．（a ）和（c ）D ．（a ）、（b ）和（c ）(8) Ⅲ级杆组应由（ B ）组成。
(a) (c)(b)图2-34A．三个构件和六个低副 B．四个构件和六个低副C．二个构件和三个低副D．机架和原动件(9)有两个平面机构的自由度都等于１，现用一个有两铰链的运动构件将它们串成一个平面机构，这时自由度等于（ B ）。
机械原理第二章练习题答案机械原理第二章练习题答案第一题：一个质量为10kg的物体以2m/s的速度向上运动，经过2s后速度变为4m/s，请问这个物体所受到的力是多少？解析：根据牛顿第二定律，力等于质量乘以加速度。
首先计算加速度，加速度等于速度变化量除以时间，即(4m/s - 2m/s) / 2s = 1m/s²。
然后将加速度代入公式，力等于质量乘以加速度，即10kg * 1m/s² = 10N。
所以这个物体所受到的力是10N。
第二题：一个力为20N的物体受到一个与其运动方向相反的恒力作用，物体的加速度为4m/s²，请问物体的质量是多少？解析：根据牛顿第二定律，力等于质量乘以加速度。
将已知数据代入公式，20N = 质量* 4m/s²。
解方程可得质量= 20N / 4m/s² = 5kg。
所以物体的质量是5kg。
第三题：一个质量为2kg的物体受到一个力为10N的作用，物体的加速度是多少？解析：根据牛顿第二定律，力等于质量乘以加速度。
将已知数据代入公式，10N = 2kg * 加速度。
解方程可得加速度 = 10N / 2kg = 5m/s²。
所以物体的加速度是5m/s²。
第四题：一个质量为5kg的物体受到一个力为30N的作用，物体的加速度是多少？解析：根据牛顿第二定律，力等于质量乘以加速度。
将已知数据代入公式，30N = 5kg * 加速度。
解方程可得加速度= 30N / 5kg = 6m/s²。
所以物体的加速度是6m/s²。
第五题：一个质量为10kg的物体受到一个力为50N的作用，物体的加速度是多少？解析：根据牛顿第二定律，力等于质量乘以加速度。
将已知数据代入公式，50N = 10kg * 加速度。
解方程可得加速度= 50N / 10kg = 5m/s²。
所以物体的加速度是5m/s²。
通过以上练习题，我们可以看到牛顿第二定律在解决物体运动问题中的应用。
2.3 试题精解和答题技巧例2-1 如例2-1图所示，已知四杆机构各构件长度：a =240mm ，b =600mm ，c =400mm ，d =500mm 。
试问：1． 当取构件4为机架时，是否存在曲柄？如存在则哪一构件为曲柄？2． 如选取别的构件为机架时，能否获得双曲柄或双摇杆机构？如果可以，应如何得到？ 解题要点：根据铰链四杆机构曲柄存在条件进行分析。
在铰链四杆机构中，其杆长条件是机构有曲柄的根本条件。
即最短杆与最长杆长度之和小于或等于其他两杆长度之和；这时如满足杆长条件，以最短或与最短杆相邻的杆为机架，机构则有曲柄；否则无曲柄；如不满足杆长条件，无论取那个构件为机架，机构均无曲柄，机构为双摇杆机构。
解： 1. 现在a+b =840mm<c+d =900mm 条件成立。
取构件4为机架时，最短杆a 为曲柄。
2. 当取最短杆a 为机架时，得双曲柄机构；若选最短杆的对杆c 为机架时，则得双摇杆机构。
例2-1图例2-2图 例2-2 试根据铰链四杆机构的演化原理，由曲柄存在条件推导如例2-2图所示偏置导杆机构成为转动导杆机构的条件。
解题要点：如例2-2图所示机构是由铰链四杆机构演化而来，本题关键在于铰链四杆机构曲柄存在条件的灵活运用。
解：因为导杆与滑块组成移动副，所以转动副中心D 在无穷远处，即： ∞→CD l ， ∞→AD l 并且 AD l ＞CD l 要使机构成为转动导杆机构，则各杆长度应满足下列条件： AB l +AD l ≤BC l +CD l AB l +(AD l -CD l )≤BC l b e a ≤+例2-3如例2-3图所示铰链四杆机构中，已知mm l BC 500=，mm l CD 350=，mm l AD 300=，AD 为机架。
试问：1．若此机构为曲柄摇杆机构，且AB 为曲柄，求AB l 的最大值； 2． 若此机构为双曲柄机构，求AB l 的最小值； 3． 若此机构为双摇杆机构，求AB l 的的取值范围。
解题要点：在铰链四杆机构由曲柄的条件中，其杆长条件是机构 例2-3图有曲柄的根本条件。
若满足杆长条件，以最短杆或与最短杆相邻的杆为机架，机构则有曲柄；否则无曲柄；若不满足杆长条件，无论取哪个构件为机架，机构均无曲柄，即为双摇杆机构。
解：1. 因AD 为机架，AB 为曲柄，故AB 为最短杆，有mm l l l l BC AD CD AB 150500300350=-+=-+≤ mm l AB 150max=2． 因AD 为机架，AB 及CD 均为曲柄，故AD 杆必为最短杆，有下列两种情况： 若BC 为最长杆，则500=<BC AB l l ，且CD AB BC AD l l l l +≤+ 故 mm l l l l CD BC AD AB 450350500300=-+=-+≥ 得 500450<≤AB l若AB 为最长杆，则500=>BC AB l l ，且CD BC AB AD l l l l +≤+ 故 mm l l l l AD CD BC AB 550300350500=-+=--≤ 得 550500<<AB l mm l AB 450min =3．如果机构尺寸不满足杆长条件，则机构必为双摇杆机构。
若AB l 为最短杆，则AD CD BC AB l l l l +>+故 mm mml l l l l AB BC AD CD AB 150150500300350max ==-+=-+> 若AB l 为最长杆，则CD BC AB AD l l l l +>+故 mm l l l l AD BC BC AB 550300350500=-+=-+> 若AB l 即不是最短杆，也不是最长杆，则ADBC AB CD l l l l +>+故 mm l l l l CD BC AD AB 450350500300=-+=-+<若要保证机构成立，则应有mm l l l l AD CD BC AB 1150300350500=++=++<故当该机构为双摇杆机构时, AB l 的取值范围为mm 150<mm l AB 450<和mm l mm AB 1150550<<.例2-4 如例2-4图所示铰链四杆机构中，已知杆杆长度mm l AB 20=，mm l BC 60=，mm l CD 85=，mm l AD 50=。
要求：1． 试确定该机构是否有曲柄；2． 判断此机构是否存在急回运动，若存在，试确定其极位夹角，并估计形成速比系数； 3． 若以构件AB 为原动件，试画出该机构的最小传动角和最大传动角的位置； 4． 回答：在什么情况下此机构有死点位置？(a) (b)例2-4图 解题要点：本题机构分析表明，四杆机构的分析常常涉及机构的类型，急回运动，传动角及死点位置这四个方面的问题。
机构类型的判别关键是确定机构是否存在曲柄；机构急回运动分析关键是确定机构的极位夹角θ和传动角γ大小的确定，除用作图法外，还可以用解析法进行精确求解，但是求解比较繁琐。
解：1. mm l l CD AB 1058520=+=+mm l l BC AD 1105060=+=+<，且连架杆AB 为最短杆，故该机构有曲柄，且AB 杆为曲柄。
此机构为曲柄摇杆机构。
2. 取mm mm l /1=μ作摇杆CD 处两极位时机构位置图D C AB 11和D C AB 22如例2-4(b)图所示，图中21AC C ∠θ=为极位夹角，且由图量得59=θ，故此机构有急回运动，可求得：98.1)59180/()59180()180/()180(≈-+=-+=θθK3. 若曲柄AB 为原动件，则机构在曲柄AB 与机架AD 共线的两位置时存在最小传动角和最大传动角。
用作图法作出机构在这两个位置D C B A ''和D C B A ''''，由图可知：55max =''∠=D C B γ, 15min =''''∠=D C B γ4. 若以曲柄AB 为主动件，则从动件摇杆CD 与连杆BC 所夹的锐角为机构的传动角γ（即BCD ∠）。
因不存在0=γ的位置，故机构无死点位置。
若以摇杆CD 为主动件，则从动件曲柄AB 与连杆BC 所夹的锐角为机构的传动角γ。
此时，机构存在曲柄AB 与连杆BC 共线两位置即传动角0=γ的位置，故机构存在两个死点位置。
例2-5如例2-5图所示六杆机构。
已知1ω、1ϕ，各杆长度及位置，求滑块5的速度F ν及构件4的角速度4ω。
例2-5图 解题要点：用瞬心法求解此题时，只要找出构件2及构件4的绝对瞬心，便可求出F ν 及4ω。
瞬心法的缺点有：①不能作机构的加速度分析；②瞬心靠作图来找，机构在运动时位置不断变化，顺心的位置也随着变化。
有时瞬心将落在图纸外，使解题发生困难。
解： 1. 延长1216P P 、3623P P ，两线交点26P 即为构件2的绝对瞬心。
12P 是构件1和构件2的相对瞬心，则l AB B P P l v μωω⋅⋅=⋅=261221 126122ωμω⋅⋅=lABP P l12612262426242ωμωAB l E l P P P P P P v ⋅=⋅⋅= (向下)（l μ为机构比例尺）2. 构件4上E 、F 两点的绝对速度方向已知，分别作E v 、F v 的垂线，两垂线相交于46P 点，便是构件4 的绝对瞬心。
构件4 的角速度4ω为 AB ll El P P P P P P P P v 126122624262426244ωμμω⋅⋅⋅=⋅=1261226244645262446454ωμωAB l F l P P P P P P P P P P v ⋅⋅⋅=⋅⋅=例2-6 1. 找出例2-6(a)中六杆机构的所有瞬心位置。
2. 角速度比24/ωω是多少？3. 角速度比25/ωω是多少？4. 求点C 的速度。
26P(a) (b) 例2-6解题要点：当用瞬心法求两构件之角速度比或某点速度比时，用到的仅为几个与求解有关的瞬心，故在题目中不要求找出所有的瞬心时，则用哪个瞬心找哪个瞬心，此外求构件上某点的速度时，可能有多种求解方法。
在进行分析时应力求简便；构件间的速度瞬心与构件所处的位置有关，瞬心法求出的构件间的角速比或构件的速度具有瞬时性，当机构运动至下一瞬心后，构件间的瞬心位置将发生相应变化，构件间的角速比及构件上某点的速度也发生相应变化。
解： 1. 找瞬心位置时，首先分析此六杆机构的瞬心数15=N 。
它们是：16P 、15P 、14P 、13P 、12P 、26P 、25P 、24P 、23P 、36P 、35P 、34P 、46P 、45P 、56P 。
为确保找对以上瞬心，可利用例2-6(b)图所示的瞬心多边形。
多边形各顶点上的数字代表机构中各构件的编号，两顶点之间的连线代表一个瞬心。
各瞬心位置可用所学知识定出：两构件直接组成转动副时，转动副中心即为两构件的瞬心；两构件组成移动副时，可运用“三心定理”。
所求瞬心位置如例2-6(a)图所示。
2． 求24/ωω即因24P 构件2与构件4上的等速重合点，故有l l P P P P μωμω⋅⋅=⋅⋅24144241222414241224//P P P P =ωω 3． 求25/ωω找出构件2与构件5的等速重合点即25P ，则： l l P P P P μωμω⋅⋅=⋅⋅25155251222515251225//P P P P =ωω4． 求C 的速度C 为杆5上的点，故 l C C P v μω⋅⋅=1552251525125/ωω⋅=P P P P故 l C P P C P P P v μω⋅⋅⋅=22515152512/另外由于C 点亦为滑块6上的点，滑块6上各点速度相等，故也可用26P 求得l P C P P v v μω⋅⋅==2261226例2-7 如例2-7(a)图所示齿轮连杆机构中，已知构件1的角速度为1ω，求图示位置构件3的角速度3ω。
(a)(b)例2-7图解题要点：此题为含有高副机构的速度分析题。
在确定组成高副的两构件的瞬心位置时，应分析在接触点处是否为纯滚动，若是纯滚动，则接触点即为瞬心；若不是纯滚动，则瞬心在过接触点的公法线上。
只要找出绝对速度瞬心35P 、15P 和相对速度瞬心13P ，即可根据瞬心的概念求出3ω。
解：先标出直接可确定的瞬心位置12P 、15P 、23P 、34P 、45P 、14P 。
先需求出瞬心35P、13P ，作出瞬心多边形如例2-7(b)图所示。
