5达朗伯原理
- 格式:ppt
- 大小:7.66 MB
- 文档页数:68





达朗伯原理
埃利斯·达朗伯(Ernst Darmbach)的原理是20世纪著名的概率统计家,也是
贝叶斯统计学诞生的催化剂。
达朗伯原理是他主要的成果,也称为达朗伯表达,是用逻辑统计学来推导事件可能性的一种方法。
达朗伯原理可以合理地推断不确定因素,包括条件及概率等,从而计算出综合结果。
基本的达朗伯原理因子包括条件独立性,事件概率和传递概率。
比如,考虑一个实验,事件A和B发生后,观察另外一个事件C的概率。
通常情况下,先考虑
条件独立性,即A和B事件发生后C事件发生的概率是确定的,比如0.5;这就是事件概率。
接下来,考虑传递概率,即A和B事件发生首先发生的概率组合。
比如,A和B事件同时发生的概率为0.3,则A和B两个条件发生后,C事件发生的概率等于0.3*0.5=0.15。
达朗伯原理使用概率统计学的观点推断出有可能性的事件,它可以把不确定性减少到最低,而且应用范围广泛,并且非常有效,例如保险、航空安全等行业,单个事件的观测结果,可以推断出更多的事件可能性,比如灾难的发生可能性,都是基于达朗伯原理之上。
总之,达朗伯原理是20世纪著名概率统计家埃利斯·达朗伯(Ernst Darmbach)发明的一种用于推断事件概率的原理。
它可以有效地降低不确定性,减少概率性风险,并且可以广泛应用于保险、航空安全和其他行业,改善安全性和可靠性。


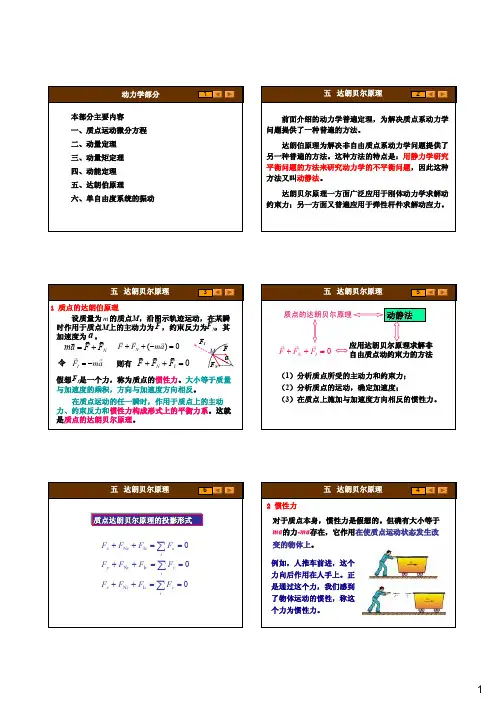
达朗伯原理和惯性力达朗贝尔原理是法国科学家达朗贝尔于1743年提出的,是分析力学的两个基本原理之一。
该原理揭示,对动力系统加入惯性力后,惯性力与外力构成平衡,因而提供一种用静力平衡方法处理动力学问题的普遍方法——动静法。
1、质点达朗贝尔原理如图1所示,质量为m 的质点沿曲线轨道运动,受主动力F 和约束力NF 作用,由牛顿第二定律有N m +=F F a即0N m +-=F Fa 引入惯性力I m =-F a (1)则有0N I ++=F F F (2)这就是质点的达朗贝尔原理:作用在质点上的所有主动力、约束力和惯性力组成平衡力系。
这样,我们完全可以采用静力学的方法和技巧,求解动力学问题。
顺便指出,达朗贝尔原理作为分析力学的基本原理之一是不需要推导证明的。
这里由牛顿第二定律导出,可以说明它与牛顿力学在数学上的等价性。
问题1 如图所示,重为G 的小球用细绳悬挂,试求AC 绳断瞬时AB 绳的张力。
答 研究小球,加惯性力I F ,受力如图所示,由质点达朗贝尔原理,有0I T ++=F G F由力三角形有 cos T F G =θ可见,加上惯性力,采用静力学中三力平衡的几何法求解决,直观简便。
2、惯性力的概念质点的惯性力I F 可以想象为:当质点加速运动时外部物质世界作用在质点上的一个场力,其大小等于质点的质量与其加速度的乘积,方向与质点加速度方向相反。
惯性力与万图1 质点达朗贝尔原理 I F 问题1图有引力是完全等效的。
惯性力与参考系相关,如图2(a)所示,小球在旋转水平圆台上沿光滑直槽运动。
在地面惯性参考系观察,小球运动的绝对轨迹为螺旋线,见图2(b),在水平面内受滑槽侧壁对它的作用力N F 作用,加速度如图所示;从转动圆台非惯性参考系观察,小球的运动轨迹沿槽直线,在半径方向,受牵连法向惯性力2()n n Ie Ie F mr ω=F 作用,小球沿直槽加速向外运动。
在垂直半径方向,小球受约束力N F 、哥氏惯性力IC F 与牵连切向惯性力Ie τF 作用处于相对平衡,见图2(a)。


达朗伯原理
达朗伯原理是热力学中的一个基本定律,它描述了能量的转换和热力学系统中的能量守恒关系。
达朗伯原理的提出对于热力学的发展具有重要的意义,它为我们理解能量转化和热力学系统的行为提供了重要的理论基础。
达朗伯原理最早由法国科学家萨迪·卡诺在19世纪中期提出,并被后来的热力学家进一步发展和完善。
该原理的核心思想是,在一个封闭的热力学系统中,能量不能自发地从低温物体传递到高温物体,而只能在高温物体和低温物体之间进行传递或转化。
这一原理揭示了热力学系统中能量流动的规律,为热机和制冷机的工作原理提供了重要的理论支持。
达朗伯原理的重要性在于它为热力学系统中能量转化的过程建立了基本的限制条件。
在实际应用中,我们可以利用达朗伯原理来分析和优化热力学系统的能量转化过程,提高能源利用效率,减少能量的浪费。
此外,达朗伯原理还为我们理解自然界中许多现象提供了重要的依据,如地球大气环流、海洋环流等都受到达朗伯原理的制约。
在工程领域,达朗伯原理也有着广泛的应用。
例如,在热力学系统的设计和优化中,我们可以根据达朗伯原理来选择合适的工作物质和工作条件,以提高系统的能量转化效率。
在制冷技术中,达朗伯原理也为我们提供了重要的理论指导,帮助我们设计出更加高效节能的制冷设备。
总之,达朗伯原理作为热力学中的基本定律,对于我们理解能量转化和热力学系统的行为具有重要的意义。
它不仅为我们提供了分析和优化热力学系统的理论基础,也为工程技术的发展提供了重要的指导和支持。
通过深入研究和应用达朗伯原理,我们可以更好地利用能源资源,推动绿色能源和可持续发展的进程。

第16章达朗伯( D′Alembert)原理※引言※几个工程实际问题※质点的惯性力与动静法※质点系的达朗伯原理※刚体惯性力系的简化※动绕定轴转动刚体的轴承动反力※结论与讨论引言♉引进惯性力的概念,将动力学系统的二阶运动量表示为惯性力,进而应用静力学方法研究动力学问题——达朗伯原理(动静法)。
♉达朗伯原理为解决非自由质点系的动力学问题提供了有别于动力学普遍定理的另外一类方法。
♉达朗伯原理一方面广泛应用于刚体动力学求解动约束力;另一方面又普遍应用于弹性杆件求解动应力。
几个工程实际问题爆破时烟囱怎样倒塌几个工程实际问题几个工程实际问题sF I F NFm axzyO mAF N ——约束力;F ——主动力;§16-1 惯性力·质点的达朗伯原理根据牛顿定律m a =F + F NF + F N -m a =0F I =-m a F + F N +F I =0——质点的惯性力。
非自由质点的达朗伯原理作用在质点上的主动力和约束力与假想施加在质点上的惯性力,形式上组成平衡力系。
F I =-m aF + F N +F I =0应用达朗伯原理求解非自由质点动约束力的方法动静法1、分析质点所受的主动力和约束力;2、分析质点的运动,确定加速度;3、在质点上施加与加速度方向相反的惯性力。
非自由质点达朗贝尔原理的投影形式00N N =++=++=++I I y y y x x x F F F F F F F F FωBACll l lααO 1x 1y 1例题16-1离心调速器已知:m 1-球A 、B 的质量;m 2-重锤C 的质量;l -杆件的长度;ω-O 1 y 1轴的旋转角速度。
求:ω-α的关系。
解:1、分析受力:以球B (或A )和重锤C 为研究对象,分析所受的主动力和约束力BF F T2CF T3F T1′2、分析运动:施加惯性力。
球绕O 1y 1轴作等速圆周运动,惯性力方向与法向加速度方向相反,其值为F I =m 1l ω2sin αF IBF F T2CF T3F T1′F I3、应用动静法:)cos (00)sin (sin 0T2T111T2T1211=-+=∑=+-=∑αααωF F g m F F F l m F y x 对于重锤CT1T12T1T3T1cos 2F F gm F F F ===''',,α对于球Bg l m m m 2121cos ωα+=例题16-2y振动筛平衡位置Oy=a sin t求:颗粒脱离台面的最小振动频率平衡位置Oy yma m g F NF I解:通过分析受力、分析运动并施加惯性力,确定颗粒脱离台面的位置和条件。