现代控制理论 第4章传递函数矩阵的状态空间实现共30页文档
- 格式:ppt
- 大小:551.00 KB
- 文档页数:30



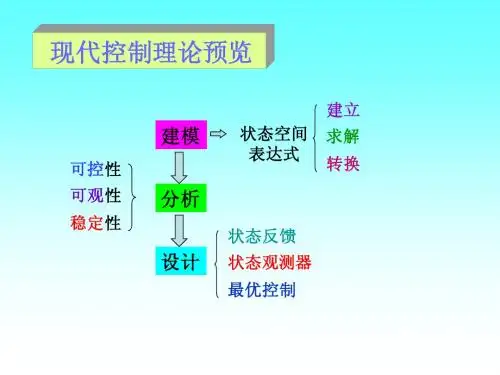

III、综合部分第四早线性多变量系统的综合与设计4.1引言前面我们介绍的内容都属于系统的描述与分析。
系统的描述主要解决系统的建模、各种数学模型(时域、频域、内部、外部描述)Z间的相互转换等;系统的分析,则主要研究系统的定量变化规律(如状态方程的解,即系统的运动分析等)和定性行为(如能控性、能观测性、稳定性等)。
而综合与设计问题则与此相反,即在己知系统结构和参数(被控系统数学模型)的基础上,寻求控制规律,以使系统具有某种期望的性能。
一般说来,这种控制规律常取反馈形式,因为无论是在抗干扰性或鲁棒性能方面,反馈闭环系统的性能都远优于非反馈或开环系统。
在本章中,我们将以状态空间描述和状态空间方法为基础,仍然在吋域中讨论线性反馈控制规律的综合与设计方法。
4. 1. 1问题的提法给定系统的状态空间描述若再给定系统的某个期望的性能指标,它既可以是时域或频域的某种特征量(如超调量、过渡过程时间、极、零点),也可以是使某个性能函数取极小或极大。
此时,综合问题就是寻求一个控制作用u,使得在该控制作用下系统满足所给定的期望性能指标。
对于线性状态反馈控制律u = -Kx + r对于线性输岀反馈控制律u = -Ffy + r其中r e R'为参考输入向量。
由此构成的闭环反馈系统分别为x - {A- BK)x+ Br y-Cx或x = {A-BHC)x+Br y = Cx闭坏反馈系统的系统矩阵分别为九=A — BKA H=A-BHC即工K = (A—BK,B,C)或工〃=(A—BHC,B,C)°闭环传递函数矩阵G K⑶=C '[si-(A-BK)Y] BG H G) = C_,[si-(A-BHOf B我们在这里将着重指出,作为综合问题,将必须考虑三个方面的因素,即1)抗外部干扰问题;2)抗内部结构与参数的摄动问题,即鲁棒性(Robustness)问题;3)控制规律的工程实现问题。
一般说来,综合和设计是两个有区别的概念。


《现代控制理论》MOOC课程1.4从状态空间表达式求传递函数矩阵一. 传递函数矩阵的定义定义:对于多输入-多输出线性定常系统,输入向量为,输出向u =u 1u 2⋯u r T 量为, 且假定初始状态为零。
分别表示的拉氏y =y 1y 2⋯y m T ෝu i s ,ෝy i s u i ,y i ොy 1s =w 11s ොu 1s +w 12s ොu 2s +⋯+w 1r s ොu r sොy 2s =w 21s ොu 1s +w 22s ොu 2s +⋯+w 2r s ොu r s⋮ොy m s =w m1s ොu 1s +w m2s ොu 2s +⋯+w mr s ොu r sෝy (s)=ොy 1(s)⋮ොy m (s)=w 11s⋯w 1r s⋮⋯⋮w m1s⋯w mr s ොu 1(s)⋮ොu r (s)=W (s )ෝu (s )写成向量形式:称为系统的传递函数矩阵。
W (s )变换,表示第j 个输入端到第i 个输出端的传递函数,系统的输入输出关系可描述为:w ij (s )x=A x+Bu x0=0y=C x+Du结论:对应于状态空间描述W(s)=C(sI−A)−1B+D 其传递函数矩阵为:证明:lims→∞W s=D且有:W(s)并且,当D≠0时,为真有理分式矩阵,当D=0时,为严格真有理分式矩阵,W s对状态空间表达式取拉氏变换:s X(s)=AX(s)+BU(s)Y(s)=CX(s)+DU(s)由状态方程的拉氏变换表达式可得:X(s)=(sI−A)−1B U(s)Y(s)=(C(sI−A)−1B+D )U(s)代入输出方程的拉氏变换表达式可得:故传递函数矩阵为:W(s)=C(sI−A)−1B+D对于传递函数矩阵:W(s )=C (sI −A )−1B +D 考虑:(sI −A)−1=Τadj(sI −A )det (sI −A )且伴随矩阵每个元素多项式的最高次幂都小于的最高次幂,故adj (sI −A )det (sI −A )lim s→∞W s =D因此有:lim s→∞(sI −A )−1=0当D =0时,为严格真有理分式;W s 故当D ≠0时,为真有理分式;W s三. 传递函数矩阵的唯一性证明:一个系统的状态空间表达式是非唯一的,但其传递函数矩阵是唯一的。



传递函数矩阵的状态空间最小实现传递函数矩阵最小实现方法——降阶法人们在设计复杂系统时,总是希望在构造系统之前用模拟计算机或数字计算机对所设计的系统进行仿真,以检查系统性能是否达到指标要求。
给定严格真传递函数矩阵()G s ,为寻找一个维数最小的(A,B,C ),使1()()C sI A B G s --=,则称该(A,B,C )是()G s 的最小实现,也称为不可约实现。
最小实现是系统实现的一种非常重要的实现方式,关于最小实现的特性,有下列几个重要结论:(1)(A,B,C )为严格真传递函数矩阵()G s 的最小实现的充要条件是(A,B )能控且(A,C )能观测。
(2)严格真传递函数矩阵()G s 的任意两个最小实现(A,B,C )与(,,)A B C 之间必代数等价,即两个最小实现之间由非奇异线性变换阵T 使得式子11,,A T AT B T B C CT --===成立。
(3)传递函数矩阵()G s 的最小实现的维数为()G s 的次数n δ,或()G s 的极点多项式的最高次数。
为了寻求传递函数矩阵的最小实现,就意味着要把系统中不能控和不能观测的状态变量消去而不至于影响系统的传递函数。
求最小实现的方法有三种:1、降阶法。
根据给定的传递函数矩阵()G s ,第一步先写出满足()G s 的能控型实现,第二步从中找出能观测子系统;或者第一步先写出满足()G s 的能观测型实现,第二步从中找出能控子系统,均可求得最小实现。
2、直接求取约当型最小实现的方法。
若()G s 诸元容易分解为部分分式形式,运用直接求取约当型最小实现的方法是较为方便的。
3用汉克尔矩阵法求取最小实现的方法。
下面主要研究降阶法(先求能控型再求能观测子系统的方法)并举例说明。
先求能控型再求能观测子系统的方法设(p ×q )传递函数矩阵()G s ,且p <q 时,优先采用本法。
取出()G s 的第j 列,记为j ()G s ,是j u 至()y s 的传递函数矩阵,有j ()G s =1[()....()]Tj qj g s g s =11()()[]()()j qj T j qj p s p s q s q s记()j d s 为1()j q s ,()qj q s 的最小公倍式,则j ()G s =11[()()]()T j qj j n s n s d s设()j d s =1,1,1,0jj j nn j n j j s a sa s a --++++则12,1,2,1,0()j j j j n n ij ij n ij n ij ij n s sss ββββ----=++++ ,1,...i q =在此()j d s 是q 个子系统传递函数的公共部分,由单输入-多输出系统的实现可知,能用能控规范Ⅰ型的j A 、j b 实现()j d s ,由()ij n s 的诸系数确定j C ,这时j ()G s 的实现为1,0,0,10j j j jn j j j j n n n I A a a a --⨯⎡⎤=⎢⎥---⎢⎥⎣⎦ 1001j j n b ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦1,01,11,1,0,1,1j j q n jj j j n j qj qj qj n C ββββββ⨯--⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 令1,,j p =,便可得j ()G s 的实现为12n nP A A A A ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦ 12n pP b b B b ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦[]12q n P C C C C ⨯=当p <q 时,显见A 、B 、C 的维数均较小,且有1pj j n n ==∑。

《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解:由图,令32211,,x u x i x i c ===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论实验报告学院:机电学院学号:XXXXX姓名:XXXXX班级:XXXX实验一 系统的传递函数阵和状态空间表达式的转换一、实验目的1.熟悉线性系统的数学模型、模型转换。
2.了解MATLAB 中相应的函数 二、实验内容及步骤 1.给定系统的传递函数为1503913.403618)(23++++=s s s s s G 要求(1)将其用Matlab 表达;(2)生成状态空间模型。
2.在Matlab 中建立如下离散系统的传递函数模型y (k + 2) +5y (k +1) +6y (k ) = u (k + 2) + 2u (k +1) +u (k ) 3.在Matlab 中建立如下传递函数阵的Matlab 模型⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++++++++++=726611632256512)(2322s s s s s s s s s s s s G 4.给定系统的模型为)4.0)(25)(15()2(18)(++++=s s s s s G求(1)将其用Matlab 表达;(2)生成状态空间模型。
5.给定系统的状态方程系数矩阵如下:[]0,360180,001,0100011601384.40==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=D C B A用Matlab 将其以状态空间模型表示出来。
6.输入零极点函数模型,零点z=1,-2;极点p=-1,2,-3 增益k=1;求相应的传递函数模型、状态空间模型。
三、实验结果及分析 1. 程序代码如下:num = [18 36];den = [1 40.3 391 150]; tf(num,den) ss(tf(num,den))Transfer function:18 s + 36----------------------------s^3 + 40.3 s^2 + 391 s + 150a =x1 x2 x3x1 -40.3 -24.44 -2.344x2 16 0 0x3 0 4 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 1.125 0.5625d =u1y1 0Continuous-time model.2.2.程序代码如下:num=[1 2 1];den=[1 5 6];tf(num,den,-1)运行结果:Transfer function:z^2 + 2 z + 1-------------z^2 + 5 z + 6Sampling time: unspecified3.程序代码如下:num={[1 2 1],[1 5];[2 3],[6]};den={[1 5 6],[1 2];[1 6 11 6],[2 7]};tf(num,den)Transfer function from input 1 to output...s^2 + 2 s + 1#1: -------------s^2 + 5 s + 62 s + 3#2: ----------------------s^3 + 6 s^2 + 11 s + 6Transfer function from input 2 to output...s + 5#1: -----s + 26#2: -------2 s + 74. 程序代码如下:sys=zpk(-2,[-15 -25 -0.4],18)ss(sys)运行结果:1)Zero/pole/gain:18 (s+2)---------------------(s+15) (s+25) (s+0.4)2)a =x1 x2 x3x1 -0.4 1.265 0x2 0 -15 1x3 0 0 -25b =u1x1 0x2 0x3 8c =x1 x2 x3y1 2.846 2.25 0d =u1y1 0Continuous-time model.5.程序代码如下:A=[-40.4 -138 -160;1 0 0;0 1 0];B=[1 0 0]';C=[0 18 360];D=0;ss(A,B,C,D)运行结果:a =x1 x2 x3x1 -40.4 -138 -160x2 1 0 0x3 0 1 0b =u1x1 1x2 0x3 0c =x1 x2 x3y1 0 18 360d =u1y1 0Continuous-time model.6. 程序代码如下:sys=zpk([1 -2],[-1 2 -3],1) tf(sys)ss((sys)运行结果:Zero/pole/gain:(s-1) (s+2)-----------------(s+1) (s+3) (s-2)Transfer function:s^2 + s - 2---------------------s^3 + 2 s^2 - 5 s - 6a =x1 x2 x3x1 -1 2.828 1.414x2 0 2 2x3 0 0 -3b =u1x1 0x2 0x3 2c =x1 x2 x3y1 -0.7071 1 0.5d =u1y1 0Continuous-time model.四、实验总结本次实验主要是熟悉利用matlab建立线性系统数学模型以及模型间的相应转换(如状态空间、传递函数模型等)、并了解matlab中相应函数的使用,如tf、ss、zp2ss、ss2tf等。
第二章 线性系统的状态空间分析法§1 线性系统的状态空间描述 §2 线性定常连续系统的分析 §3 线性定常离散系统的分析 §4 系统的传递函数矩阵一、定义及表达式零初始条件下,输出向量的拉氏变换式与输入向量 的拉氏变换式之间的传递关系——传递函数矩阵。
& ⎧ x(t ) = Ax(t ) + Bu(t ) ⇒ sX(s ) = AX(s ) + BU (s ) ⎨ ⎩y (t ) = Cx(t ) + Du(t ) ⇒ Y(s ) = CX(s ) + DU(s )∴ X(s ) = (sI − A ) BU (s )−1∴ Y(s ) = C(sI − A ) BU (s ) + DU(s ) = G (s )U(s )−1G (s ) = C(sI − A ) B + D−1q× p1⎡Y1 (s )⎤ ⎡G11 (s ) G12 (s ) L G1 p (s )⎤ ⎡U1 (s ) ⎤ ⎢Y (s )⎥ ⎢G (s ) G (s ) L G (s )⎥ ⎢U (s )⎥ 22 2p ⎢ 2 ⎥ = ⎢ 21 ⎥⎢ 2 ⎥ ⎢ M ⎥ ⎢ M M M ⎥⎢ M ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢Yq (s )⎥ ⎢Gq1 (s ) Gq 2 (s ) L Gqp (s )⎥ ⎢U p (s )⎥ ⎣ ⎦ ⎣ ⎦⎣ ⎦Y1 (s ) = G11 (s )U1 (s ) + G12 (s )U 2 (s ) + L + G1 j (s )U j (s ) + L + G1 p (s )U p (s )Yi (s ) = Gi1 (s )U1 (s ) + Gi 2 (s )U 2 (s ) + L + Gij (s )U j (s ) + L + Gip (s )U p (s )Yq (s ) = Gq1 (s )U1 (s ) + Gq 2 (s )U 2 (s ) + L + Gqj (s )U j (s ) + L + Gqp (s )U p (s )Gij (s ) =Yi (s ) , i = 1,2, L , q; j = 1,2 ,L ,p U j (s )第 j 个输入与第i 个输出之间的传递函数。