北大版高等数学第一章 函数及极限答案 习题1.3-推荐下载

高等数学北大版教材答案为了帮助学生更好地学习高等数学北大版教材，下面提供一些常见题目的答案。

请注意，由于篇幅限制，以下仅列举一部分题目的答案。

1. 题目1:求函数$f(x)=\sqrt{x^2+1}-x$的极限$\lim\limits_{x\to\infty}f(x)$。

解答：首先，我们可以对函数$f(x)$进行简化，将根式进行有理化。

利用差平方公式可得：$f(x) = \frac{(\sqrt{x^2+1})^2-x^2}{\sqrt{x^2+1}+x} =\frac{1}{\sqrt{x^2+1}+x}$接下来，我们考虑当$x\to\infty$时，函数$f(x)$的极限。

由于$x$趋向无穷大，可以忽略1与$x^2$的对比，即$\sqrt{x^2+1}\approx x$。

那么：$\lim\limits_{x\to\infty}f(x) =\lim\limits_{x\to\infty}\frac{1}{\sqrt{x^2+1}+x} =\lim\limits_{x\to\infty}\frac{1}{2x} = 0$所以，$\lim\limits_{x\to\infty}f(x) = 0$。

2. 题目2:求函数$f(x)=\int_0^x(2t^2+3t)dt$的原函数$F(x)$。

解答：根据定积分的性质，我们可以通过求导的方式求得函数$f(x)$的原函数$F(x)$。

首先，对被积函数进行求导：$\frac{d}{dx}(2t^2+3t) = 4t+3$得到被积函数的导函数为$4t+3$。

接下来，我们对导函数积分得到原函数：$F(x) = \int (4t+3)dt = 2t^2+\frac{3}{2}t+C$所以，函数$f(x)$的原函数$F(x)$为$2t^2+\frac{3}{2}t+C$。

3. 题目3:已知函数$f(x)$在点$x=1$处的导数为$3$，求曲线$y=f(x)$在点$(1,f(1))$处的切线方程。

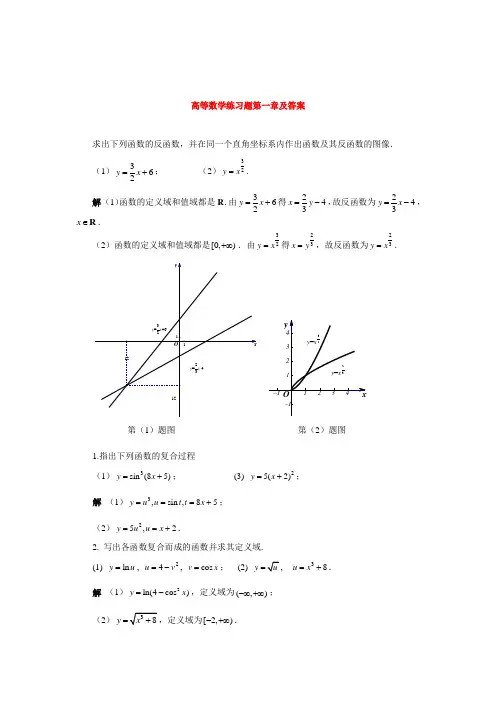
高等数学练习题第一章及答案求出下列函数的反函数，并在同一个直角坐标系内作出函数及其反函数的图像．（1）362y x =+； （2）32y x =.解 （1）函数的定义域和值域都是R ．由362y x =+得243x y =-，故反函数为243y x =-，x ∈R ．（2）函数的定义域和值域都是[0,)+∞．由32y x =得23x y =，故反函数为23y x =．第（1）题图 第（2）题图1.指出下列函数的复合过程（1）3sin (85)y x =+； (3) 25(2)y x =+； 解 （1）3,sin ,85y u u t t x ===+； （2）25,2y u u x ==+．2. 写出各函数复合而成的函数并求其定义域.(1) ln y u =, 24u v =-, cos v x =；(2) y , 38u x =+． 解 （1）2ln(4cos )y x =-，定义域为(,)-∞+∞；（2）y =[2,)-+∞．练习1.1.31．某款手机价格为P 时，需求量Q 关于P 的需求函数P Q 210-=，当价格3=P 时，求Q 的值．【解】(3)10234Q =-⨯=．2．设某商品的价格函数是Q P 318000-=（单位：元），求该商品的收益函数，并求销售1000件商品时的总收益和平均收益．【解】211()(8000)800033R Q PQ Q Q Q Q ==-=-．1. 利用函数图像求下列极限.(1) 0lim x x C → (C 为常数) ；(2) 1lim ()2x x →+∞；(3) lim 2x x →-∞； (4) 0lim sin x x →；解 做出相应的函数图像（略）．（1）观察常函数y C =的图像知，0lim x x C C →=；（2）观察函数1()2x y =的图像知，1lim()02x x →∞=；（3）观察函数2x y =的图像知，11lim 2lim()lim 022x x x x x x →-∞→∞→∞===；（4）观察函数sin y x =的图像知，0limsin sin00x x →==．2. 作出函数 2,01()3,12x x f x x x ⎧=⎨-<⎩，≤≤≤ 的图像，并求1lim ()x f x →.解 函数图像如下：第2题图观察图像知，1lim ()2x f x →=．计算下列极限：(1) 22lim(352)x x x →-+ ； (2) 342lim 31x x xx x →∞+-+；(3) 233lim 1x x x →-+ ； (4) 239lim 3x x x →--．解 (1) 222222lim(352)3lim 5lim lim 2121024x x x x x x x x →→→→-+=-+=-+=；(2) 3224224241111lim lim lim lim 03131311lim 1lim lim x x x x x x x x x x x x x x x x xx x →∞→∞→∞→∞→∞→∞→∞+++===-+-+-+； (3) 3322333lim lim 33lim 01lim lim1x x x x x x x x x →→→→→--==++； (4) 23339(3)(3)lim lim lim(3)633x x x x x x x x x →→→--+==+=--．练习1.2.3（1）当1x →时，比较无穷小 1x - 和 31x -．（2）当1→x 时，比较无穷小 1x - 和21(1)2x -．解 （1）3221111(1)(1)lim lim lim(1)311x x x x x x x x x x x→→→--++==++=--，所以，当1x →时， 1x - 和 31x -为同阶无穷小； （2）21111(1)1(1)(1)12lim lim lim(1)11212x x x x x x x x x →→→--+==+=--， 所以，当1x →时，1x -和21(1)2x -为等阶无穷小，即当1x →时，1x -～21(1)2x -．设函数21,0,()2,01,3, 1.x x f x x x x x -<⎧⎪=⎨⎪->⎩≤≤（1）作出函数图像，讨论函数在0x =及1x =处的连续性； （2）指出函数的连续区间. 解 （1）函数图像如下：y x123–1–2–1–2–3123O练习题1.3.1图观察图像知，函数在0x =处不连续，在1x =处的连续； （2）函数的连续区间为(,0)-∞与[0,)+∞． 1．计算下列极限：（1）2lim 2x x →； （2）322lim61x x x →-+++；（3）01lim1cos x x →+； （4）2π3lim sin x x →．解（1）函数2x y =是初等函数，定义域为R ，故22lim 224x x →==；（2）函数2261x y x -+=++是初等函数，定义域为[2,)+∞．故3223223lim461361x x x →-+-+==++++； （3）函数11cos y x =+是初等函数，定义域为{}|(21)π,x x k k ≠-∈Z ．故0111lim1cos 1cos02x x →==++．2．利用高级计算器求方程321109140x x x ++-=...的实数近似解（精确到0.0001）．解 设置保留4位小数，在输入窗格输入“321109140x x x ++-=...”，点击输入，显示：．练习1.4.1某人把50万元借给某公司10年，约定以复利计息，年利率为6%，那么10年末他的本利和为多少？假设一年按平均12期计息，那么10年末他的本利和为多少？假设计息练习1.4.2假设年利率为5%，现在投资多少元，20年末可以得到100万元？【解】200100(15%)37.6889A -=⨯+≈（万元）．。

（完整版）函数与极限习题与答案第⼀章函数与极限（A ）⼀、填空题 1、设x x x f lg lg 2)(+-=，其定义域为。

2、设)1ln()(+=x x f ，其定义域为。

3、设)3arcsin()(-=x x f ，其定义域为。

4、设)(x f 的定义域是[0，1]，则)(sin x f 的定义域为。

5、设)(x f y =的定义域是[0，2] ，则)(2x f y =的定义域为。

6、432lim23=-+-→x kx x x ，则k= 。

7、函数xxy sin =有间断点，其中为其可去间断点。

8、若当0≠x 时，xxx f 2sin )(= ，且0)(=x x f 在处连续，则=)0(f 。

9、=++++++∞→)21(lim 222nn nn n n n n Λ。

10、函数)(x f 在0x 处连续是)(x f 在0x 连续的条件。

11、=++++∞→352352)23)(1(lim xx x x x x 。

12、3)21(lim -∞→=+e nknn ，则k= 。

13、函数231x1是⽐3-+x 15、当0→x 时，⽆穷⼩x --11与x 相⽐较是⽆穷⼩。

16、函数xe y 1=在x=0处是第类间断点。

17、设113--=x x y ，则x=1为y 的间断点。

18、已知33=??πf ，则当a 为时，函数x x a x f 3sin 31sin )(+=在3π=x 处连续。

19、设??>+<=0)1(02sin )(1x ax x xxx f x 若)(lim 0x f x →存在，则a= 。

20、曲线2sin 2-+=xxx y ⽔平渐近线⽅程是。

21、114)(22-+-=x x x f 的连续区间为。

22、设??>≤+=0,cos 0,)(x x x a x x f 在0=x 连续，则常数a= 。

⼆、计算题1、求下列函数定义域（1）211xy -= ；（2）x y sin = ；（3）x2、函数)(x f 和)(x g 是否相同？为什么？（1）x x g x x f ln 2)(,ln )(2 == ；（2）2)(,)(x x g x x f == ；（3）x x x g x f 22tan sec )(,1)(-== ；3、判定函数的奇偶性（1）)1(22x x y -= ；（2）323x x y -= ；（3）)1)(1(+-=x x x y ；4、求由所给函数构成的复合函数（1）22,sin ,x v v u u y === ；（2）21,x u uy +==；5、计算下列极限（1）)2141211(lim n n ++++∞→Λ；（2）2)1(321lim nn n -++++∞→Λ；（3）35lim 22-+→x x x ；（4）112lim 221-+-→x x x x ；（5）)12)(11(lim 2x x x -+∞→；（6）2232) 2(2lim -+→x x x x ；（7）x x x 1sin lim 20→；（8）xx x x +---→131lim 21 ；（9）)1(lim 2x x x x -++∞→；6、计算下列极限（1）xwx x sin lim 0→；（2）x x→；（4）xx xx )1(lim +∞→；（5）1)11(lim -∞→-+x x x x ；（6）x x x 10)1(lim -→；7、⽐较⽆穷⼩的阶（1）32220x x x x x --→与，时；（2）)1(21112x x x --→与，时；8、利⽤等价⽆穷⼩性质求极限（1）30sin sin tan lim x x x x -→；（2）),()(sin ) sin(lim0是正整数m n x x m n x →；9、讨论函数的连续性。

高等数学iCourse教材答案第一章：函数与极限1. 函数的概念和性质函数是数学中重要的概念之一。

函数是一种特殊的关系，它将一个集合中的每个元素映射到另一个集合中的唯一一个元素。

函数可以用数学符号表示为f(x)，其中x是自变量，f(x)是因变量。

2. 极限的定义与性质极限是函数中非常重要的概念之一。

极限描述了函数在某个点上的趋势和变化。

根据极限的定义，当自变量无限接近某个值时，函数的值也会无限接近一个值。

3. 极限的计算方法计算极限时，可以运用一些基本的极限计算方法，例如代入法、夹逼准则、无穷小代换法等。

这些方法可以帮助我们求解更复杂的极限问题。

4. 函数的连续性连续性是函数的一个重要性质，它描述了函数在某个区间上的平滑程度和无间断性。

如果函数在某个点上连续，则该函数在该点的左、右极限存在且相等。

第二章：导数与微分1. 导数的定义与性质导数描述了函数在某个点上的变化速率。

在数学中，导数用来研究函数的变化趋势和曲线的斜率。

导数的定义是函数在某点的极限，可以通过差商的极限来求得。

2. 导数的计算方法计算导数时，可以运用一些基本的求导法则，例如常数法则、幂法则、和差法则、乘积法则、商法则等。

这些方法可以帮助我们求解更复杂的导数问题。

3. 函数的微分与微分法微分是函数运算中的一种重要方法，它描述了函数在某个点上的线性变化。

微分法是求导数的基本方法，可以帮助我们求得偏导数、高阶导数以及应用问题中的相关导数。

4. 应用问题的求解导数和微分在应用问题中的求解中起着重要的作用。

例如，可以利用导数和微分求解最值问题、优化问题、曲线的切线与法线等。

第三章：微分中值定理与导数的应用1. 罗尔定理与拉格朗日中值定理罗尔定理和拉格朗日中值定理是微分中值定理的两个重要定理。

罗尔定理描述了函数在某个区间的两个端点上取相同值的情况，而拉格朗日中值定理描述了函数在某个区间内必然存在某个点，该点的切线斜率与区间的平均斜率相等。

2. 高阶导数与泰勒展开高阶导数是导数的延伸，它描述了函数变化的更高阶性质。

习题1-11. 下列函数是否相等,为什么? 函数 函数的概念 函数相同的条件222(1)()();(2)sin (31),sin (31);1(3)(),() 1.1f xg x y x u t x x f x g x x x ===+=+-==+- 解: (1)相等.因为两函数的定义域相同,都是实数集R ;x =知两函数的对应法则也相同;所以两函数相等.(2)相等.因为两函数的定义域相同,都是实数集R ,由已知函数关系式显然可得两函数的对应法则也相同,所以两函数相等.(3)不相等.因为函数()f x 的定义域是{,1}x x x ∈≠R ,而函数()g x 的定义域是实数集R ,两函数的定义域不同,所以两函数不相等. 2. 求下列函数的定义域 函数 函数的概念 定义域和值域的概念211(1)arctan ;(2);lg(1)(3); (4)arccos(2sin ).1y y x x xy y x x ==-==-解: (1)要使函数有意义,必须40x x -≥⎧⎨≠⎩ 即 4x x ≤⎧⎨≠⎩ 所以函数的定义域是(,0)(0,4]-∞.(2)要使函数有意义,必须30lg(1)010x x x +≥⎧⎪-≠⎨⎪->⎩即 301x x x ≥-⎧⎪≠⎨⎪<⎩所以函数的定义域是[-3,0)∪(0,1).(3)要使函数有意义,必须210x -≠ 即 1x ≠±所以函数的定义域是(,1)(1,1)(1,)-∞--+∞.(4)要使函数有意义,必须12sin 1x -≤≤ 即 11sin 22x -≤≤ 即ππ2π2π66k x k -+≤≤+或5π7π2π2π66k x k +≤≤+,(k 为整数). 也即ππππ66k x k -+≤≤+ (k 为整数).3. 设1()1x f x x -=+,求1(0),(),().f f x f x-函数函数的概念 函数的基本运算解: 10(0)110f -==+,1()1(),1()1x x f x x x --+-==+--1111().111x x f x x x--==++ 4. 设1,10()1,02x f x x x -≤<⎧=⎨+≤≤⎩,求(1)f x -.函数函数的概念 函数的基本运算解: 1,1101,01(1).(1)1,012,13x x f x x x x x -≤-<≤<⎧⎧-==⎨⎨-+≤-≤≤≤⎩⎩5. 设()2,()ln x f x g x x x ==,求(()),(()),(())f g x g f x f f x 和(())g g x . 函数函数的概念 复合函数的概念解: ()ln (())22,g x x x f g x ==(())()ln ()2ln 2(ln 2)2,x x x g f x f x f x x ==⋅=⋅()2(())22,(())()ln ()ln ln(ln ).xf x f f xg g x g x g x x x x x ====6. 求下列函数的反函数及其定义域:函数 反函数、复合函数 反函数的定义2531(1); (2)ln(2)1;1(3)3; (4)1cos ,[0,π].x xy y x xy y x x +-==+++==+∈ 解: (1)由11x y x -=+解得11yx y-=+, 所以函数11x y x -=+的反函数为1(1)1xy x x-=≠-+. (2)由ln(2)1y x =++得1e 2y x -=-,所以,函数ln(2)1y x =++的反函数为1e 2()x y x -=-∈ R .(3)由253x y +=解得31(log 5)2x y =- 所以,函数253x y +=的反函数为31(log 5)(0)2y x x =-> .(4)由31cos y x =+得cos x =又[0,π]x ∈,故x =又由1cos 1x -≤≤得301cos 2x ≤+≤,即02y ≤≤,故可得反函数的定义域为[0,2],所以,函数31cos ,[0,π]y x x =+∈的反函数为(02)y x =≤≤.7. 判断下列函数在定义域内的有界性及单调性:函数 函数的特性 有界性、单调性2(1); (2)ln 1xy y x x x==++ 解: (1)函数的定义域为(-∞,+∞), 当0x ≤时,有201x x ≤+,当0x >时,有21122x x x x ≤=+, 故(,),x ∀∈-∞+∞有12y ≤.即函数21xy x =+有上界.又因为函数21xy x =+为奇函数,所以函数的图形关于原点对称,由对称性及函数有上界知,函数必有下界,因而函数21xy x =+有界. 又由1212121222221212()(1)11(1)(1)x x x x x x y y x x x x ---=-=++++知,当12x x >且121x x <时,12y y >,而 当12x x >且121x x >时,12y y <. 故函数21xy x=+在定义域内不单调. (2)函数的定义域为(0,+∞),10,0M x ∀>∃>且12;e 0M x M x >∃>>,使2ln x M >.取012max{,}x x x =,则有0012ln ln 2x x x x M M +>+>>, 所以函数ln y x x =+在定义域内是无界的. 又当120x x <<时,有12120,ln ln 0x x x x -<-<故1211221212(ln )(ln )()(ln ln )0y y x x x x x x x x -=+-+=-+-<. 即当120x x <<时,恒有12y y <,所以函数ln y x x =+在(0,)+∞内单调递增.8. 已知水渠的横断面为等腰梯形,斜角ϕ=40°,如图所示.当过水断面ABCD 的面积为定值S 0时,求湿周L (L =AB +BC +CD )与水深h 之间的函数关系式,并指明其定义域.函数 函数的概念 定义域、值域的概念图1-1解:011()(2cot )(cot )22S h AD BC h h BC BC h BC h ϕϕ=+=++=+ 从而 0cot S BC h hϕ=-. 000()22cot sin sin 2cos 2cos 40sin sin 40L AB BC CD AB CD S h hBC h hS S h h h h ϕϕϕϕϕ=++==+=+---=+=+ 由00,cot 0S h BC h hϕ>=->得定义域为0tan 40)S .9. 下列函数是由哪些基本初等函数复合而成的?函数 基本初等函数 基本初等函数5122412(1)(1);(2)sin (12);1(3)(110);(4).1arcsin 2xy x y x y y x-=+=+=+=+解: (1)124(1)y x =+是由124,1y u u x ==+复合而成.(2)2sin (12)y x =+是由2,sin ,12y u u v v x ===+复合而成. (3)512(110)x y -=+是由152,1,10,w y u u v v w x ==+==-复合而成.(4)11arcsin 2y x=+是由1,1,arcsin ,2y u u v v w w x -==+==复合而成.习题1-21. 写出下列数列的通项公式,并观察其变化趋势:极限 数列极限的概念与性质 数列极限的定义1234579(1)0,,,,,; (2)1,0,3,0,5,0,7,0,; (3)3,,,,.3456357----解: 1(1),1n n x n -=+当n →∞时,1n x →. 1(2)cos π2n n x n -=,当n 无限增大时,有三种变化趋势:趋向于+∞,趋向于0,趋向于-∞.21(3)(1)21nn n x n +=--,当n 无限增大时,变化趁势有两种,分别趋于1,-1. 2. 对下列数列求lim n n a x →∞=,并对给定的ε确定正整数()N ε,使对所有()n N ε>,有n x a ε-<:极限数列极限的概念与性质 数列极限的定义1π(1)sin ,0.001; (2)0.0001.2n n n x x n εε==== 解: (1)lim 0n n a x →∞==,0ε∀>,要使11π0sin 2n n x n n ε-=<<,只须1n ε>.取1N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,必有0n x ε-<. 当0.001ε=时,110000.001N ⎡⎤==⎢⎥⎣⎦或大于1000的整数.(2)lim 0n n a x →∞==,0ε∀>,要使0n x ε-==<=<1ε>即21n ε>即可.取21N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,有0n x ε-<. 当0.0001ε=时, 821100.0001N ⎡⎤==⎢⎥⎣⎦或大于108的整数. 3. 根据数列极限的定义，证明:极限 数列极限的概念与性质 数列极限的定义21313(1)lim0;(2)lim ;212(3)1;(4)lim 0.999 1.n n n n n n n n →∞→∞→∞→∞-==+== 个证: (1)0ε∀>,要使22110n n ε=<-,只要n >.取N =,则当n>N 时,恒有210nε<-.故21lim 0n n →∞=. (2) 0ε∀>,要使555313,2(21)4212n n n n n ε-=<<<-++只要5n ε>,取5N ε⎡⎤=⎢⎥⎣⎦,则当n>N 时,恒有313212n n ε-<-+.故313lim212n n n →∞-=+. (3) 0ε∀>,要使2221a n ε=<<-,只要n >,取n =,则当n>N 时,1ε<,从而1n →∞=. (4)因为对于所有的正整数n ,有10.99991n <-个,故0ε∀>,不防设1ε<,要使1,0.999110n n ε=<-个只要ln ,ln10n ε->取ln ,ln10N ε-⎡⎤=⎢⎥⎣⎦则当n N >时,恒有,0.9991n ε<-个故lim 0.9991n n →∞=个.4. 若lim n n x a →∞=,证明lim n n x a →∞=,并举反例说明反之不一定成立.极限 函数极限的概念与性质 函数极限的定义证:lim 0n n x →∞=,由极限的定义知,0,0N ε∀>∃>,当n N >时,恒有n x a ε-<.而 n n x x a a ε-<-<0,0N ε∴∀>∃>,当n N >时,恒有n x a ε-<,由极限的定义知lim .n n x a →∞=但这个结论的逆不成立.如(1),lim 1,nn n n x x →∞=-=但lim n n x →∞不存在.5. 利用收敛准则证明下列数列有极限,并求其极限值:极限数列极限的概念与性质数列极限的定义1111(1)1,2,; (2)1,1,1,2,.1nn n nx x x n x x n x ++=====+=+证: (1)122x =<,不妨设2k x <,则12k x +=<=.故对所有正整数n 有2n x <,即数列{}n x 有上界.又1n n n x x x +-==0>,又由2n x <从而10n n x x +->即1n n x x +>,即数列{}n x 是单调递增的.由极限的单调有界准则知,数列{}n x 有极限. 设lim n n x a →∞=,则a =于是22a a =,2,0a a ==(不合题意,舍去),lim 2n n x →∞∴=.(2) 因为110x =>,且111nn nx x x +=++, 所以02n x <<, 即数列有界又 111111111(1)(1)n n n n n n nn n n x x x x x x x xx x --+---⎛⎫⎛⎫++-=-= ⎪ ⎪++++⎝⎭⎝⎭ 由110,10n n x x -+>+>知1n n x x +-与1n n x x --同号， 从而可推得1n n x x +-与21x x -同号， 而 1221131,1,022x x x x ==+=-> 故10n n x x +->, 即1n n x x +>所以数列{}n x 单调递增，由单调有界准则知，{}n x 的极限存在. 设lim n n x a →∞=, 则11a a a=++， 解得1122a a +==(不合题意，舍去). 所以1lim 2n n x →∞=习题1-31. 选择题 （1）设1,1()0,1x f x x ≠⎧=⎨=⎩，则0lim ()x f x →=（D ）A.不存在B.∞C.0D.1（2）设()f x x =，则1lim ()x f x →=（B ） A.1- B.1 C.0 D.不存在（3）0(0)f x +与0(0)f x -都存在是函数()f x 在点0x x =处有极限的一个（A ）A.必要条件B.充分条件C.充要条件D.无关条件（4）函数()f x 在点0x x =处有定义，是当0x x →时()f x 有极限的（D ）A.必要条件B.充分条件C.充分必要条件D.无关条件 （5）设1()1x f x x -=-，则1lim ()x f x →=（D ） A.0 B.1- C.1 D.不存在 2.证明01lim arctanx x→不存在. 0000011lim arctan ,lim arctan ,2211lim arctan lim arctan ,1limarctan x x x x x x x x xx ππ+-+-→→→→→==-∴≠∴不存在。

第一章总练习题221.:581 2.3|58|1422.|58|6,586586,.3552(2)33,52333,015.5(3)|1||2|1(1)(2),2144,.22|2|,.2,2,4,2;2,3x x x x x x x x x x x x x x x x x y x x x y x y x y x y x y x -≥-≥-≥-≥-≤-≥≤-≤-≤-≤≤≤+≥-+≥-+≥-+≥=+-≤=+≤=->=求解下列不等式（）或或设试将表示成的函数当时当时解解解2.解222312312,4,(2).32,41(2), 4.313.1.22,4(1)44,0.1,0.4.:1232(1)2.222221211,.22123222n n y x y y y x y y x x x x x x x x x x n n n n ->=--≤⎧⎪=⎨->⎪⎩<+≥-<++<++>≥-≠+++++=-+==++的全部用数学归纳法证明下列等式当时,2-等式成立设等式对于成立,则解证1231111121211222112312222222124(1)(1)3222,22221..1(1)(2)123(1).(1)1(11)1(1)1,(1)(1)n n n n n n n n n n n n n n n n n n n n n x nx x x nxx x x x x n x x ++++++-+++++=++++++++-+++=-+=-=-+-++++++=≠--++-===--即等式对于也成立故等式对于任意正整数皆成立当时证1,1212.1(1)123(1)(1)(1)n n n nnn n x nx x x nxn x n x x +--++++++++=++-等式成立设等式对于成立,则122122112211221221(1)(1)(1)(1)1(1)(12)(1)(1)1(1)(2)(1)(1)1(1)(2)(1)(1)1(2)(1),(1)1n n n n n n n n n n n n n n n n n n n x nx x n x x n x nx x x n x x n x nx x x x n x n x nx x x x n x n x n x x n ++++++++++-+++-+=--+++-++=--+++-++=--+++-++=--+++=-+即等式对于成立.,.|2|||25.()(1)(4),(1),(2),(2);(2)();(3)0()(4)224211222422(1)(4)1,(1)2,(2)2,(2)0.41224/,2(2)()x x f x xf f f f f x x f x x f f f f x x f x +--=---→→----------==--==-====----≤-=由归纳原理等式对于所有正整数都成立设求的值将表成分段函数当时是否有极限:当时是否有极限?解00022222222;2,20;0,0.(3).lim ()2,lim ()0lim ().(4).lim ()lim (4/)2,lim ()lim 22lim (),lim () 2.6.()[14],()14(1)(0),x x x x x x x x x x x f x f x f x f x x f x f x f x f x x f x x f →-→+→-→--→--→-+→-+→--→-⎧⎪-<≤⎨⎪>⎩==≠=-======--无因为有设即是不超过的最大整数.求003,;2(2)()0?(3)()?391(1)(0)[14]14,1467.[12]12.244(2).lim ()lim[14]14(0).(3).()12,()x y x x f f f x x f x x f f f f x y f f x f x →→+⎛⎫⎪⎝⎭==⎛⎫⎡⎤⎡⎤=-=-=-=-+=-=-=- ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦=-=-==-的值在处是否连续在连续因为不连续因为解111111.7.,0,,:(1)(1);(2)(1).n n n n n n a b a b n b a b a n b n a b a b a++++=-≤<--<++<--设两常数满足对一切自然数证明1111111()()(1),(1).118.1,2,3,,1,1.:{},{}..111,1,7,111n n n n n n n n n n n n nn n n n n n n b a b a b b a a b b b b n b b a b a b a n a b an a b n n a b a b a b n nn ++--+++--+++=<+++=+--->+-⎛⎫⎛⎫==+=+ ⎪ ⎪⎝⎭⎝⎭<+=++⎛+ ⎝类似有对令证明序列单调上升而序列单调下降,并且令则由题中的不等式证证=11111111111(1)1,111111111(1)11(1)1111111,11111.1111(1)11n n nn n nn nn nn n n n n n n n n n n n n n n n n n n n n n +++++++⎫⎛⎫-+⎪ ⎪+⎛⎫⎭⎝⎭<++ ⎪⎝⎭-+⎛⎫⎛⎫⎛⎫+-+<++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+-+<+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫+<+ ⎪ ⎪+⎝⎭⎝⎭⎛⎫+ ⎛⎫⎝⎭++< ⎪+⎝⎭111111121111111111(1)1111(1)11111111111111111.1111111.111n n nn n nn n n n n n n n n n n n n n n n n n nn n n n n +++++++⎛⎫-+⎪ ⎪+⎝⎭-+⎛⎫⎛⎫⎛⎫++<+-+ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+<+-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+++<+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫++>+ ⎪++⎝⎭⇔我们证明22111211111(1)11..(1)(1)1111,1,1,11.nn n n n n n n n n n n e e e n n n n ++++>+++++⇔>++⎛⎫⎛⎫⎛⎫⎛⎫→∞+→+→+<<+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭最后不等式显然成立当时故9.求极限22222222221111lim 1111234111111112341324351111().2233442210.()lim (00, ()lim n n n n n n n n n n n n nxf x a nx ax nxf x nx a →∞→∞→∞⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭++==→→∞=≠+===+作函数)的图形.解解0;1/,0.x x ⎧⎨≠⎩1111.?,()[,]|()|,[,].,(),[,],max{||,||}1,|()|,[,].,|()|,[,],(),[,].12.f x a b M f x M x a b M N f x N x a b M M N f x M x a b M f x M x a b M f x M x a b <∀∈≤≤∀∈=+<∀∈<∀∈-<<∀∈1在关于有界函数的定义下证明函数在区间上为有界函数的充要条件为存在一个正的常数使得设存在常数使得M 取则有反之若存在一个正的常数使得则证12121212:()()[,],()()()()[,].,,|()|,|()|,[,].|()()||()||()|,|()()||()||()|,[,].113.:()cos 0y f x y g x a b f x g x f x g x a b M M f x M g x M x a b f x g x f x g x M M f x g x f x g x M M x a b f x x x xπ==+<<∀∈+≤+<+=<∀∈==证明若函数及在上均为有界函数则及也都是上的有界函数存在证明在的任一证,0().11(,),00,,,(),1()(,)0,()(21/2)cos(21/2)0,21/20().n x f x M n n M f n M n nf x f x n n n x f x δδδδδδπ→->><>=>-=→=++=→∞+→n 邻域内都是无界的但当时不是无穷大量任取一个邻域和取正整数满足和则故在无界.但是x 故当时不是无穷大量证11111000114.lim (1)ln (0).1ln 1,ln ln(1),.lim lim 10.ln(1)ln(1)lim lim ln(1)ln lim(1)ln 1,ln (1)ln ().ln(1)15.()()nn nn n n n n y y y y y n nn n x x x xx y x y n y x n y y y y e y y xn x x n y f x g x →∞→∞→∞→→→-=>-==+==-=++=+=+==-=→→∞+证明令则注意到我们有设及在实轴上有证00002022222220000.:()(),,()lim ()lim ()().1cos 116.lim.22sin 1cos 2sin 1sin 12lim lim lim lim 1422n n n n n x x x y y f x g x x x x f x f x g x g x x x x x y y x x y y →∞→∞→→→→→→===-=⎛⎫-==== ⎪⎝⎭定义且连续证明若与在有理数集合处处相等,则它们在整个实轴上处处相等.任取一个无理数取有理数序列证明证证0011000000001.2ln(1)17.:(1)lim 1;(2)lim .ln(1)(1)lim lim ln(1)ln lim(1)ln 1.(1)11(2)lim lim lim lim ln(1)ln(1)lim1.1x a xa y x y y y y y x a a a x x aa ax x x y y a a y e e e y x y y y e ye e e e e y e e e y x x x y ye e +→→→→→+→→→→→=+-==+=+=+==---====++==证明证0111018.()lim ()0,()lim ()()0.|()|,0||.0,0,0|||()|/.min{,},0||,|()()||()||()|,li x ax ay f x a f x y g x a f x g x g x M x a x a f x M x a f x g x f x g x M Mδεδδεδδδδεε→→====<<-<>><-<<=<-<=<=设在点附近有定义且有极限又设在点附近有定义,且是有界函数.证明设对于任意存在使得当时令则时故证m ()()0.x af xg x →=19.()(,),,()()|()|() () ()(),()(,).y f x c g x f x f x c g x c f x cc f x c g x g x =-∞+∞≤⎧⎪=>⎨⎪-<-⎩-∞+∞设在中连续又设为正的常数定义如下 当当当试画出的略图并证明在上连续0000000000000|()|,0,||lim ()lim ()()().(),0,||()lim ()lim ().(),().0,,0,x x x x x x x x f x c x x g x f x f x g x f x c x x f x c g x c c g x f x c g x c c δδδδεεδ→→→→<>-<===>>-<>=====><>一若则存在当时|f(x)|<c,g(x)=f(x),若则存在当时,g(x)=c,若则对于任意不妨设存在使证()0000121212|||()|.||.(),()(),|()()||()|,(),(),|()-()|0.()()min{(),}max{(),}().max{(),()}(|()()|()())/2.min x x f x c x x f x c g x f x g x g x f x c f x c g x c g x g x g x f x c f x c f x f x f x f x f x f x f x δεδεε-<-<-<≤=-=-<>==<=+--=-++得当时设若则若 则二利用证121212123123123111123{(),()}(|()()|(()())/2.120.()[,],[()()()],3,,[,].[,],().()()(),(),.()min{(),(),()},f x f x f x f x f x f x f x a b f x f x f x x x x a b c a b f c f x f x f x f x c x f x f x f x f x f ηηη=--++=++∈∈======设在上连续又设其中证明存在一点使得若则取即可否则设证31231313000000()min{(),(),()},()(),[,],,[,],().21.()(),()g(),,.0()g()()g()x f x f x f x f x f x f x x c a b f c y f x x g x x x kf x l x x k l l kf x l x x kf x l x x ηη=<<∈==+=+≠+在连续根据连续函数的中间值定理存在一点使得设 在点连续而在点附近有定义但在不连续问是否在连续其中为常数如果在连续;如果在解,l 0,000000||()[[()lg()]()]/.22.Dirichlet ..,()1;,()0;lim (),()11(1)lim 0;(2)lim (arctan )sin 12n n n n x x x x x g x kf x x kf x l x x x x D x x x D x D x D x x x x x →→∞→+∞=+-''→→→→+⎛⎫= ⎪+⎝⎭不连续,因否则将在连续证明函数处处不连续任意取取有理数列则取无理数列则故不存在在不连续.23.求下列极限:证222001/112132100;2tan 5tan 5/5(3)lim lim 5.ln(1)sin [[ln(1)]/]sin /1lim(1).24.()[0,),0().0,(),(),,().{x x y x y n n x x x x x x x x x x x y e y f x f x x a a f a a f a a f a π→→→→+=====++++=+==+∞≤≤≥===设函数在内连续且满足设是一任意数并假定一般地试证明11},lim .lim ,(),().(),{}()0(1,2,),{}n n n n n n n n n n n n a a l a l f x x f l l a f a a a a f a n a →∞→∞++====≤=≥=单调递减且极限存在若则是方程的根即单调递减.又单调递减有下界,证111lim ,lim lim ()(lim )().25.()(,),:(0)1,(1),()()().()((,)).()()().()()n n n n n n n n n x n n a l a l a f a f a f l y E x E E e E x y E x E y E x e x E x x E x E x E nx E x +→∞→∞→∞→∞======-∞+∞==+==∀∈-∞+∞++==故有极限.设则设函数在内有定义且处处连续并且满足下列条件证明用数学归纳法易得于是证11.,()(11)(1).1(0)(())()()(),().().1111,(1)()()()(),().11()()().,n n n n n n nn mmm n n n E n E E e E E n n E n E n e E n E n e E n e n E E n E n E e E E e n n n n m E E m E e e r E n n n -=++====+-=-=--======⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭设是正整数则于对于任意整数对于任意整数即对于所有有理数lim ().,,(),()lim ()lim ().nn n r x x x x n n n r e x x E x E x E x e e e e →∞→∞→∞=→====n 对于无理数取有理数列x 由的连续性的连续性。

高等数学第一章 函数、极限、连续§1．1 函数一．求函数的定义域例1．求函数()2100ln ln ln x x x f -+=的定义域 例2．求5ln 1-+-=x x x y 的定义域例3．设()x f 的定义域为[]()0,>-a a a ，求()12-x f 的定义域 例4．设()⎩⎨⎧≤≤<≤=42 ,220 ,1x x x g 求()()()12-+=x g x g x f 的定义域，并求⎪⎭⎫ ⎝⎛23f 。

二．求函数的值域 例1．求3311-=x ey 的值域例2．求()()⎪⎩⎪⎨⎧>--≤≤---<-==2,2122,52,323x x x x x x x f y 的值域，并求它的反函数 三．求复合函数有关表达式 1．已知()x f 和()x g ，求()[]x g f 例1．已知()1-=x xx f ，求()⎥⎦⎤⎢⎣⎡-11x f f 例2．设()21x x x f +=，求()()[]()重复合n x f x f f f n =例3．设()⎩⎨⎧>≤-=2,02,42x x x x f ，求()[]x f f 2．已知()x g 和()[]x g f ，求()x f 例1．设()x e e e f x xx++=+21，求()x f例2．已知()xxxee f -='，且()01=f ，求()x f例3．设()x x fsin =，求()x f '例4．已知()x x f 2cos 3sin -=，求证()x x f 2cos 3cos += 3．已知()x f 和()[]x g f ，求()x g例．已知()()x x f +=1ln ，()[]x x g f =，求()x g 解：()[]x fx g 1-=实际上为求反函数问题()[]()[]x x g x g f =+=1ln ，()x e x g =+1 ()1-=x e x g 4．有关复合函数方程 例．设()x x f x x f 2311-=⎪⎭⎫⎝⎛-+，求()x f 四．有关四种性质例1．设()()x f x F ='，则下列结论正确的是[ ]（A ）若()x f 为奇函数，则()x F 为偶函数。

高等数学（本）第一章 函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0，问：⑴()2x f ； ⑵()x f sin ； ⑶()()0>+a a x f ； ⑷()()a x f a x f -++ ()0>a 的定义域是什么？（1）][；，－的定义域为所以知－11)(,111022x f x x ≤≤≤≤[]ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(－的定义域为所以知－由][φ时，定义域为当时，定义域为当从而得－知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a ax a a x a x班级 姓名 学号3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ，()x e x g =，求()[]x g f 和()[]x f g ，并做出这两个函数的图形。

⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明: .0lim =∞→n n n y x{}结论成立。

（完整word版）第⼀章求极限练习题答案1．求下列极限：(1) 2221lim (1)n n n n →∞++- 解：原式=2221lim 21n n n n n →∞++-+=22112lim 211n n n n n→∞++-+=2 (2) 20lim(1)x x x →+解：原式=12lim[(1)]x x x →+=2e(3) 32lim3x x →- 解：原式=3x →=x →=14(4) 1lim (1)x x x e →∞-解：原式=1(1)lim1xx e x→∞-=1(5) 0x ≠当时，求lim cos cos cos 242n n x x x→∞L .解：原式=cos cos (2cos sin )2422lim2sin 2n n n n x x x x x →∞L =1cos sin22lim 2sin 2n n nx x x →∞-=sin lim 2sin 2n nn x x →∞ =sin 2lim()sin 2n n n x x x x →∞g =sin x x(6) 21sinlim x x 解：原式=21limx x g=limx=limx=(7)22212lim()12n nn n n n n n n→∞+++++++++L 解：令2221212n ny n n n n n n n=+++++++++L 因 2222(1)(1)12122211n n n n n n ny n n n n n n n n n n ++++++++=≤≤=++++++++L L ⽽2(1)12lim 2n n n n n n →∞+=++， 2(1) 12lim 12n n n n n →∞+=++，故222121n n n n n n n n n →∞+++=++++++L(8) n →∞解：原式=2n n →∞→∞==1.3 函数的极限作业1. 根据函数极限的定义,验证下列极限: (1) 3 1lim0x x→∞= 解: 0ε?>,要使3311|0|||x x ε-=<,即||x >只要取X =,则当||x X >时,恒有 31|0|x ε-<, 所以31lim 0x x →∞=.(2) 42x →= 解: 0ε?>,要使|4||2|2x ε-=<<,则当0|4|x δ<-<时,恒有|2|ε<,所以42x →=. 2. 求下列数列极限:(1) 22212lim()12n nn n n n n n n→∞+++++++++L 解：令2221212n ny n n n n n n n =+++++++++L 因 2222(1)(1)12122211n n n n n n ny n n n n n n n n n n ++++++++=≤≤=++++++++L L ⽽2(1)12lim 2n n n n n n →∞+=++， 2(1) 12lim 12n n n n n →∞+=++，故222121lim()122n n n n n n n n n →∞+++=++++++L(2) n →∞解：原式=2n n →∞→∞==3．求下列函数极限：(1) 225lim 3x x x →+- 解：原式=-9(2) 224lim 2x x x →-- 解：原式=2 lim(2)x x →+=4(3) 21lim1x x →-解：原式=14x x →→==-(4) x →∞ 解：原式=0x =(5) 2(21)(32)lim (21)x x x x →∞--+ 解：原式=226723lim4412x x x x x →∞-+=++ (6) 2121lim()11x x x →--- 解：原式=211(1)11lim lim 112x x x x x →→---==--+ 4. 设23 2 0() 1 01 1 x>11x x f x x x x ?+≤=+<≤-? ，分别讨论()f x 在0x →，1x →和2x →时的极限是否存在.解：0lim ()2x f x -→=，0lim ()1x f x +lim ()x f x →不存在. 1lim ()2x f x -→=，1lim ()x f x +→趋向⽆穷⼤，故1lim ()x f x →不存在. 2lim ()1x f x -→=，2lim ()1x f x +→=，故2lim ()1x f x →=.1.43．求下列函数极限：(1) 225lim 3x x x →+-=-9(3) 224lim 2x x x →--=2lim(2)x x →+=4 1x →14x x →→==-(7) 000h h h →→→===(9) x →∞=0x =(11) 2(21)(32)lim (21)x x x x →∞--+=226723lim 4412x x x x x →∞-+=++(13) limlim0x x == (15) 2121lim()11x x x →---=211(1)11lim lim 112x x x x x →→---==--+ 2. 设10100()01112x x x f x x x x -?==<极限，并说明这两点的极限是否存在. 解：001lim ()lim11x x f x x --→→-==-，00lim ()lim 0x x f x x ++→→==，00lim ()lim ()x x f x f x -+→→≠ 故lim ()x f x →不存在.11lim ()lim 1x x f x x --→→==，11lim ()lim11x x f x ++→→== 11lim ()lim ()x x f x f x -+→→= 1lim ()1x f x →=. 1.51．求下列极限：(1) 0sin 3sin 3lim lim 333x x x xx x→→=?=00tan 333(3)limlim sin 444x x x x x x →→==222200022sin 222(5)lim 2sin 224()2x x x x x x x xx→→→?===? 注:在0(0,)U δ，2sin 02x ≥.222000222(5)lim 2sin24x x x x x x x →→→===(7) 02cos lim sin 2x x x →解: 原式=2021sin cos lim sin cos )2x x x x=2002sin sin lim sin 2x x x x x x →→+g =2021sin sin lim2()2x x x xx →+220sin sin 2lim ()x x x x x →=+=4 注意: 代数和中的⼀部分不能⽤⽆穷⼩替换. 错原式=0x →220212lim 1cos )4x x x x x →+ (8) 01sin cos lim1sin cos x x xx xββ→+-+-解: 原式=2022sin cos 2sin 222lim 2sin cos 2sin 222x x x x x x x βββ→++=0sin (cos sin ) 222lim sin (cos sin )222x x x x x x x βββ→++=00sin cos sin 222limlim sin cos sin222x x x x x x x x βββ→→++g =02lim 12x x x β→g =1β注意: 代数和的⼀部分不能⽤⽆穷⼩替换.错 01sin cos lim 1sin cos x x x x x ββ→+-+-=202112lim 12x x x x x βββ→+=+ 33333(9)lim(1)lim[(1)]xx x x e x x →∞→∞+=+=244424(11)lim()lim[(1)]22x x x x x e x x +---→∞→∞--=+=++330(13)lim(13)lim[(13)]x x x x x x e →→+=+=4. 当0x →时，下列函数中哪些是x 的⾼阶⽆穷⼩，哪些是x 的同阶⽆穷⼩，哪些是x的低阶⽆穷⼩？32(1)1000x x +322001000lim lim (1000)0x x x x x x x→→+=+=解：因为 321000()x x o x +=所以3(2)2sin x 32002sin sin lim lim 2sin 0x x x x x x x→→=?=解：因为 3sin ()x o x =所以(3) ln(1)x +解: 100ln(1)limlim ln(1)1x x x x x x→→+=+=因为ln(1)~x x +所以 (4) 1cos x -解: 2002sin sin1cos 22limlim lim(sin )022x x x x xxx xxx →→→-===g 因为，1cos ()x o x -=所以(5) sin x x + 解: 因为 0sin limx x x x →+=0sin lim(1)x xx→+=2，故sin x x +是x 的同阶⽆穷⼩.(6): 因为0x →=1312033sin 11lim[())cos x x xx x →g g =∞，故是x的低阶⽆穷⼩.或：因为0x →=0x →0x →x 的低阶⽆穷⼩. 思考题：1．11331lim (39)lim 9(1)3x x xx xx x x x →+∞→+∞+=+g g =1331lim 9[(1)]3x xx x x →+∞+g =90e =9 2．0arccot limx x x →=∞，因为当0x →时，arccot 2 x π→.习题2.2 1．求下列函数的导数：2(1)cos y x x =+解：'sin 2y x x =-+=2cos (sin )()'222x x x -g g =2cos (sin )22x x -gcos sin 22x x -g(7)sin 3y x =解：'3cos3y x =2(9)sin(1)y x x =++解：2'(21)cos(1)y x x x =+++3(11)ln y x =解：1139'(ln )'(3ln )'222y x x x x x=+=+=(6) 6(21)y x =+解：5'6(21)2y x =+g =512(21)x + (10) ln(ln )y x =解：1'(ln )'ln y x x ==11ln x x g(11)ln ln(sin )y x =解：1'(sin )'sin y x x =+1cos sin x x +g2．在下列⽅程中，求隐函数的导数： (1)cos()y x y =+解：'sin()(1')y x y y =-+?+(2)222333x y a +=解：113322x y y --+=3. 求反函数的导数：(1)ln y x x =+解：1111dx dy dy dx x==+(2) arcsin x y e =解：sin ln x y =，故1cos ln dx y dyy=?=4. 求下列函数的导数(1) 2sin y x x =解：'y =22sin cos x x x x + 3(3)ln y x x=23221'3ln 3ln y x x x x x x x=+=+解： (5) 1ln 1ln xy x-=+解：21ln 1ln '(1ln )x xx x y x +---=+211ln y x=-++ 22212'0(1ln )(1ln )y x x x x =-=-++ (7) 21cosy x x=解1'2cos y x x =+2x 1(sinx -12cos x x +2x 1(sin)x -(9)ln(y x ='y x =+==解：(10)12(0)xxy x e a =->解：112'2xxy xe x e =+g g(ln (x x a a a --(11) arccos ln x y x = -arccos ln(1ln xy x x=--解：1'y x=-+2arccos 1x x x =-+2arccos x x =- ln (13)x y x =2ln ln (ln )x x x y e e ?==解： ln ln 11'2ln 2ln x x y x x x x x-=??=? (14) cos (sin )xy x =解：ln cos lnsin y x x =Q ，对该式两边求导数得11'sin ln sin cos cos sin y x x x x y x=-+cos '(sin )(sin ln sin cos tan )x y x x x x x ∴=-+ (15) y x =11ln ln ln(1)ln(1)22y x x x =+--+Q ，对该式两边求导数得1111'2(1)2(1)y yxx x =---+arcsin lnx y x =-解：'[ln(1(ln )'y x =++(11x +(2)x -1x +1x4. 求反函数的导数：(1)ln y x x =+解：1111dx dy dydx x==+arcsin x y e =解：sin ln x y =，故=?=求下列参数⽅程的导数'y ： 211(1)(1)x t t y t ?=?+?=+242(1)2(1)'()1(1)1'()1(1)t t t dy y t t t dx x t t t +-?+-+===+-+解：(2)3233131at x t at y t ?=??+??=?+? 解：322332323326(1)333(2)(1)3(1)333(12)(1)at t at t dydy at t t dt dx a x at t dxa t dt t +-?-+===+-?-+(3)2ln(1)arctan x t y t t ?=+?=-? 解：222111221dy dyt dt tdx t dx t dt t-+===+2．若()F x 在点a 连续，且()0F x ≠。

第一章 函数与极限1. 设 ⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21=224sin )4(==ππϕ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0，问：⑴()2x f ； ⑵()x f sin ； ⑶()()0>+a a x f ； ⑷()()a x f a x f -++ ()0>a 的定义域是什么？（1）][；，－的定义域为所以知－11)(,111022x f x x ≤≤≤≤ []ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(－的定义域为所以知－由 ][φ时，定义域为当时，定义域为当从而得－知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a ax a ax a a x a x3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ，()xe x g =，求()[]x gf 和()[]x fg ，并做出这两个函数的图形。

⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}nx 有界, 又,0lim =∞→nn y证明:.0lim =∞→n n n y x{}结论成立。

从而时，有，当自然数即又有对有界，∴=<=-<>∃>∀=≤∀>∃∴∞→ ..0)(,0,0lim ,,0εεεεMM y x y x My N n N y Mx n M x n n n n n n n n n 5. 根据函数的定义证明: ⑴()813lim 3=-→x x8)13(lim 813303,033,33813,03=-<--<-<>∀<-<-=-->∀→x x x x x x x 所以成立时，恒有，当＝取故即可。

高等数学章节练习题及答案第一章作业1.1.11．求下列函数的定义域.(1)y ；(2) 213y x =- ；(3) πsin ,0,2π,π.2x x y x x ⎧<⎪⎪=⎨⎪<⎪⎩≤≤解 （1）解不等式243x x -+≥0得x ≤1或x ≥3；故函数定义域为(,1][3,)-∞+∞； （2）解不等式2x +≥0得x ≥2，由230x -≠知x ≠；故函数定义域为[2,)+∞； （3）分段函数的定义域为各段取值范围的并集，故定义域为[0,π)．2. 设3()21f x x x =-+，求(0),(1),(2),(1)f f f f x -+．解 (0)0011f =-+=；3(1)12112f -=--⨯-+=（）（）；3(2)22215f =-⨯+=； 33232(1)12113312213f x x x x x x x x x x +=+-++=+++--+=++（）（）3. 设23,1,()4,x x f x x -<⎧=⎨⎩≥1，求(2)f -，(0)f ，(2)f ．解 (2)23(2)8f -=-⨯-=；(0)2f =；(2)4f =．4. 求下列函数的反函数，并在同一个坐标系中作出它们的图像 （1）23y x =-； （2）21y x =-，(0,)x ∈+∞ 解 （1）函数的定义域和值域都是R ，由23y x =-得322y x =+，故其反函数为 322x y =+，x ∈R ． 它们的图像为第4（1）题图（2）函数的定义域为(0,)+∞，值域为(1,)-+∞，由21y x =-得x =为y=(1,)x ∈-+∞．它们的图像为第4（2）题图1．写出下列函数的复合过程.(1) 21x y e -= ； (2) ln(3)y x =- ； (3) y =(4) 2πsin (3)6y x =-． 解 （1）u y e =，21u x =-； （2）ln y u =，3u x=-； （3）y =tan u v =，2xv =； （4）2π,sin ,36y y u v v x ===-．2．写出各函数复合而成的函数并求其定义域 .(1) 5u y =, u = ln v x = ； (2) ln y u = ， 381u x =+.解 （1）y =[,)e +∞‘（2）3ln(81)y x =+，定义域为1(,)2-+∞．作业1.1.31．市场对某种商品的需求量Q 满足：()2002Q P P =-，其中P 为商品价格，而生产商对此商品的供应量S 满足：()3100S P P =-，求该种商品的市场均衡价格P 和均衡数量Q ．解（1）()2002Q P P =-= ()3100S P P =-得 P =60，将P =60代入()2002Q P P =-得Q =80．2．已知某商品的成本函数（单位：万元）为()608C Q Q =+，其中Q 为该商品的产量． （1）该商品的计划售价为12万元/件，那么该商品的盈亏平衡点（保本点）Q 0是多少件？ （2）求生产50件时的成本和平均成本为多少？（3）当该商品以计划售价的五折出售时，能否盈利？ 解（1）Q 0=15（件）；（2）(50)(50)100,(50)250C C C ===（万元）；（3）不会盈利，会造成亏空．3．某商品的销售价格为100元，月销售量为4000件，当销售价格每提高2元，月销售量会减少50件，在不考虑其他因素情况下，（1）求这商品月销售量与价格之间的函数关系； （2）当价格提高到多少元时，这商品会卖不出去？解（1）()650025Q P P =-；（2）260元．作业1.2.11.通过观察对应函数图像，讨论下列极限：（1）1lim1x x →∞+； （2）1lim 4x x →+∞（）；（3）lim 3x x →-∞；（4）1lim(2)x x→∞-；（5）0lim x +→（6）1limln x x →． （7）π3lim sin x x →； （8）设1,()1,x x f x x x -<⎧=⎨+⎩0,≥0，求0lim ()x f x →．解 做出相应的函数图像（略）． （1）观察函数11y x =+的图像知，1lim 01x x →∞=+；第1（1）题图 第1（2）题图（2）观察函数1()4x y =的图像知，1lim 04xx →+∞=（）；（3）观察函数3x y =的图像知，lim 30x x →-∞=；第1（3）题图（4）观察函数12y x =-（5）观察函数y =的图像知，0lim0x →=；第1（5）题图 第1（6）题图 （6）观察函数ln y x =的图像知，1limln ln10x x →==．（7）观察函数sin y x =的图像知，π3πlim sin sin3x x →=；第1（7）题图 第1（8）题图 （8）观察函数的1,()1,x x f x x x -<⎧=⎨+⎩0,≥0图像知，0lim ()x f x →=1；1.计算下列极限：（1）331lim(2)x x x→∞+-；（2）2222lim 341x x x x x →∞+--+；（3）21lim 1x x x →∞--解 （1）333131lim(2)lim2lim lim 2x x x x x x x x →∞→∞→∞→∞+-=+-=；（2）2222122222lim lim 4133413x x x x x x x x x x→∞→∞+-+-==-+-+； （3）222111lim lim 0111x x x x x x x→∞→∞--==--．2.计算下列极限：（1）324lim()x x x →+； （2）4322lim ()x x x→--；（3）222lim 2x x x →-+.解（1）3322444lim()limlim 8412x x x x x x x →→→+=+=+=；（2）443322222265lim ()lim lim 1684x x x x x x x→-→-→--=-=-=-； （3）222421lim 2222x x x →--==++.3.作出函数21,1,(),11x x f x x x -⎧<⎪=⎨-⎪⎩≥ 的图像． (1) 写出1lim ()x f x →-和2lim ()x f x →；(2) 写出1lim ()x f x -→和1lim ()x f x +→；(3) 判断1lim ()x f x →是否存在，若存在求出来．解 函数图像如图下：第3题图（1）观察函数图像知，1lim ()2x f x →-=，2lim ()3x f x →=；（2）11lim ()lim (1)0x x f x x --→→=-=，211lim ()lim (1)0x x f x x ++→→=-=；（3）因为1lim ()x f x →=1lim ()x f x +→=0，所以1lim ()x f x →存在，且1lim ()0x f x →=．4. 已知函数231,1,(),>11x x f x x x -⎧<⎪=⎨+⎪⎩,求1lim ()x f x →． 解 11lim ()lim (31)2x x f x x --→→=-=，211lim ()lim (1)2x x f x x ++→→=+=． 故 1lim ()x f x →=2.5. 利用微软高级计算器计算下列各极限（1）2lim(1)x x x →∞+；（2）0sin5lim 2x x x →；（3）0tan lim x x x →；（4）01lim sin x x x →．解（1）22lim(1)x x e x →∞+=； （2）0sin55lim 22x x x →=；（3）0tan lim1x x x →=； （4）01lim sin 0x x x→=．1.判断下列命题是否正确（正确的填“√”，错误的填“×”） （1）10000.001是无穷小； （ × ） （2）当x →-∞时，10x 是无穷小； （ × ） （3）当x →-∞时，0是无穷小； （ √ ） （4）当x →-∞时，2x 是无穷小； （ √ ） （5）当x →∞时，2x 是无穷小； （ × ） （6）当2x →时，24x -是无穷小． （ √ ）2.比较下列各组无穷小.（1）当0x →时，4x 与2x ;（2）当2x →时， 2x -与38x -;（3）当x →∞时，318x -与12x -. 解 （1）因为40lim 0x x →=，2lim 0x x →=，且42200lim lim 0x x x x x →→==，所以当0x →时，4x 是比2x 较高阶的无穷小．（2）因为2lim(2)0x x →-=，32lim(8)0x x →-=，且3222222211limlim lim 8(2)(1)17x x x x x x x x x x x →→→--===--++++， 所以，当2x →时， 2x -与38x -是同阶无穷小．（3）因为31lim08x x →∞=-，1lim 02x x →∞=-，且3233311228lim lim lim 018812x x x x x xx x x x→∞→∞→∞---===---， 所以，当2x →时，318x -为比12x -较高阶的无穷小．3.确定函数1()1x f x x +=-为无穷小的条件． 解 由于-1111lim=0111x x x →+-+=---，故函数为无穷小的条件为“ 1x →-”。

第一章函数历年试题模拟试题课后习题（含答案解析）[单选题]1、设函数，则f(x)=（）A、x(x+1)B、x(x-1)C、(x+1)(x-2)D、(x-1)(x+2)【正确答案】B【答案解析】本题考察函数解析式求解.，故[单选题]2、已知函数f(x)的定义域为[0，4]，函数g(x)=f(x+1)+f(x-1)的定义域是（）.A、[1，3]B、[-1，5]C、[-1，3]D、[1，5]【正确答案】A【答案解析】x是函数g(x)中的定义域中的点，当且仅当x满足0≤x+1≤4且0≤x-1≤4即-1≤x≤3且1≤x≤5也即1≤x≤3，由此可知函数g(x)的定义域D(g)={x|1≤x≤3}=[1,3]. [单选题]3、设函数f（x）的定义域为[0，4]，则函数f（x2）的定义域为（）.A、[0，2]B、[0，16]C、[-16，16]D、[-2，2]【正确答案】D【答案解析】根据f(x)的定义域，可知中应该满足：[单选题]4、函数的定义域为（）.A、[-1,1]B、[-1,3]C、(-1,1)D、(-1,3)【正确答案】B【答案解析】根据根号函数的性质，应该满足：即[单选题]写出函数的定义域及函数值（）.A、B、C、D、【正确答案】C【答案解析】分段函数的定义域为各个分段区间定义域的并集，故D=(－∞，-1]∪（-1，＋∞）.[单选题]6、设函数,则对所有的x，则f(-x)=（）.A、B、C、D、【正确答案】A【答案解析】本题考察三角函数公式。

.[单选题]7、设则=（）.A、B、C、D、【正确答案】B【答案解析】令则，故[单选题]8、则（）.A、B、C、D、【正确答案】D【答案解析】[单选题]9、在R上，下列函数中为有界函数的是（）.xA、eB、1＋sin xC、ln x【正确答案】B【答案解析】由函数图像不难看出在R上e x,lnx,tanx都是无界的，只有1+sinx可能有界，由于|sinx|≤1,|1+sinx|≤1+|sinx|≤2所以有界.[单选题]10、不等式的解集为（）.A、B、C、D、【正确答案】D【答案解析】[单选题]11、（）.A、B、C、D、【正确答案】A【答案解析】根据二角和公式，[单选题]12、函数的反函数是（）.A、B、C、D、【正确答案】A【答案解析】由所以，故.[单选题]13、已知则（）.A、B、C、D、【正确答案】C【答案解析】[单选题]14、已知为等差数列，，则（）.A、-2B、1C、3D、7【正确答案】A因为同理可得：故d=a4－a3=－2.[单选题]15、计算（）.A、B、C、D、【正确答案】A【答案解析】根据偶次根式函数的意义，可知，故[单选题]16、计算（）.A、0B、1C、2D、4【正确答案】C【答案解析】原式=[单选题]将函数|表示为分段函数时，=（）.A、B、C、D、【正确答案】B【答案解析】由条件[单选题]18、函数f(x)=是（）.A、奇函数B、偶函数C、有界函数D、周期函数【正确答案】C【答案解析】易知不是周期函数，,即不等于，也不等于，故为非奇、非偶函数.，故为有界函数.[单选题]19、函数,则的定义域为（）.A、[1,5]C、(1,5]D、[1,5)【正确答案】A【答案解析】由反正切函数的定义域知：，故定义域为[1,5].[单选题]20、下列等式成立的是()A、B、C、D、【正确答案】B【答案解析】A中(e x)2=，C中，D中[单选题]21、下列函数为偶函数的是()A、y=xsinxB、y=xcosxC、y=sinx+cosxD、y=x(sinx+cosx)【正确答案】A【答案解析】sinx是奇函数，cosx是偶函数。

6
高等数学习题集
(5) lim 1 x 1 x ；
x0
x
(6)
lim
x1

x
1 1

3 x3 1

．
3.
设
lim
x

x2 1 x 1

ax

b


0,
求 a 和 b 的值．
7
高等数学习题集
§1.6 极限存在准则 两个重要极限
1. 选择题.
(1)
lim
x x0
f
(x )存在是
f (x) 在 x0 的某一去心领域内有界的______ 条件.
(2)
设函数
ax2 f (x)
2x 1
x 1, 且 lim f (x) 存在，则 a _____. x 1 x1
3* 根据函数极限的定义证明：
(1)
lim
x
1 x3 2x3
x x0
x x0
A) lim f x lim f x
x x0
x x0
C) lim f x 不一定存在 x x0
(2) lim x2 9 (
).
x3 x 3
).
B) lim f x lim f x
x x0
x x0
1 x sin x 1
(题集
§1.8 函数的连续性与间断点
1. 选择题.
(1) 设 f x 在 x x0 处 连 续 , 且 存 在 0 , 使 当 0 x x0 时 有 f x 0, 则
(
)．
A) f x0 0

北大版高等数学第一章函数及极限答案习题1.2（范文）第一篇：北大版高等数学第一章函数及极限答案习题1.2（范文）习题 1.2 1.求下列函数的定义域:(1)y=ln(x2-4);(2)y=ln1+x5x-x211-x;(3)y=ln4;(4)y=2x2+5x-3.解(1)x2-4>0,|x|2>4,|x|>2,D=(-∞,-2)⋃(2,+∞).(2)1+x1-x>0.⎧⎨1-x>0或⎧1-x<0⎩1+x>0⎨⎩1+x<0.-1<x<1,D=(-1,1).(3)5x-x24>1,x2-5x-4<0.x2 -5x+4=0,(x-1)(x-4)=0,x1=1,x2=4.D=(1,4).(4)2x2+5x-3>0.(2x-1)(x+3 )=0,x1=-3,x2=1/2.D=(-∞,-3)⋃(1/2,+∞).2.求下列函数的值域f(X),其中X为题中指定的定义域.(1)f(x)=x2+1,X=(0,3).f(X)=(1,10).(2)f(x)=ln(1+sinx),X=(-π/2,π],f(X) =(-∞,ln2].(3)f(x)=3+2x-x2,X=[-1,3],3+2x-x2=0,x2-2x-3=0,(x+1)(x-3 )=0,x1=-1,x2=3,f(X)=[0,f(1)]=[0,4].(4)f(x)=sinx+cosx,X=(-∞,+∞).f(x)= 2(sinxcos(π/4)+cosxsin(π/3))=2sin(x+π/4),f(X)=[-2,2].3.求函数值：设f(x)=lnx2(1)ln10,求f(-1),f(-0.001),f(100);(2)设f(x)=arcsinx1+x2,求f(0),f(1),f(-1);(3)设f(x)=⎧⎨ln(1-x),-∞<x≤0,⎩-x, 0<x<+∞,求f(-3),f(0),f(5).⎧cosx,0≤x<1,(4)设f(x)=⎪⎨1/2, x=1,求f(0),f(1),f(3/2),f(2).⎪⎩2x, 1<x≤3解(1)f(x)=logx2,f(-1)=log1=0,f(-0.001)=log(10-6)=-6,f(100)=log104 =4.(2)f(0)=0,f(1)=arcsin(1/2)=π/6,f(-1)=arcsin(-1/2)=-π/6.(3)f(-3)=l n4,f(0)=0,f(5)=-5.(4)f(0)=cos0=1,f(1)=1/2,f(3/2)=22,f(2)=4.4.设函数f(x)=2+x2-x,x≠±2,求f(-x),f(x+1),f(x)+1,f⎛1⎫1⎝x⎪⎭,f(x).解f(-x)=2-x2+x+13+x2+x,x≠±2;f(x+1)=2-x-1=1-x,x≠1,x≠-3,2+x4⎛1⎫2-1/x2x-1+1=,x≠±2;f ⎪==,x≠0,x≠±1/2,2-x2-x⎝x⎭2+1/x2x+11 2+x=,x≠±2.f(x)2-xf(x+∆x)-f(x)5.设f(x)=x3,求，其中∆x为一个不等于零的量.∆xf(x+∆x)-f(x)(x+∆x)3-x3x3+3x2∆x+3x∆x2+∆x3-x3解===3x2+3∆x+∆x2.∆x∆x∆x6.设f(x)=lnx,x>0,g(x)=x2,-∞<x<+∞,试求f(f(x)),g(g(x)),f(g(x)),g(f(x)).f(x)+1=解f(f(x))=f(lnx)=lnlnx,x>1;g(g(x))=g(x2)=x4,-∞<x<+∞;f(g(x))=f(x2)=lnx 2,x≠0;g(f(x))=g(lnx)=ln2x,x>0.⎧0, x≥0,⎧x, x≥0;7.设f(x)=⎨g(x)=⎨求f(g(x)),g(f(x)).-x,x<0;1-x,x<0,⎩⎩解∀x,g(x)≥0,f(g(x))=0.⎧g(0), x≥0,⎧0, x≥0,g(f(x))=⎨=⎨g(-x),x<0.⎩⎩-x,x<0.8.作下列函数的略图:(1)y=[x],其中[x]为不超过x的最大整数;(2)y=[x]+x;1(3)y=sinhx=(ex-e-x)(-∞<x<+∞);21(4)y=coshx=(ex+e -x)(-∞<x<+∞);2⎧x2, 0≤x<0,(5)y=⎨⎩x-1,-1≤x<0.（1）（2）（3）（4）（5）⎧x29.设f(x)=⎨,x≥0,求下列函数并且作它们的图形⎩x, x<0,:(1)y=f(x2);(2)y=|f(x)|;(3)y=f(-x);(4)y=f(|x|).解(1)y=x4,-∞<x<+∞.(2)y=|f(x)|=⎧⎨x2,x≥0，⎩-x, x<0.(3)y=f(-x)=⎧⎨x2,-x≥0,⎧x2,x≤0,⎩-x, -x<0=⎨⎩-x, x>0.(4)y=f(|x|)=x2,-∞<x<+∞.3求下列函数的反函数:(1)y=x2-2x(0<x<+∞);(2)y=sinhx(-∞<x<+∞);(3)y=coshx(0<x<+∞).解(1)x2-2x=y,x2-2yx-4=0,x=y+y2+4,y=x+x2+4(-∞<x<+∞).ex-e-x(2)=y ,z=ex,z2-2yz-1=0,ex=z=y+y22+1,x=ln(y+y2+1),y=ln(x+x2+1),(-∞<x< +∞).(3)ex+e-x2=y,z=ex,z2-2yz+1=0,ex=z=y+y2-1,x=ln(y+y2-1),y=ln (x+x2-1),(x≥1).证明cosh2x-sinh2x=1.⎛ex+e-x⎫2⎛ex-e-x⎫2(e2x证coshx-sinhx=+e-2x+2)-(e2x+e-2x22-2)⎝2⎪⎭-⎝2⎪⎭=4=1.下列函数在指定区间内是否是有界函数?(1)y=ex2,x∈(-∞,+∞);否(2)y=ex2x∈(0,1010);是(3)y=lnx,x∈(0,1);否(4)y=lnx,x∈(r,1),其中r>0.是2(5)y=e-x2+sinx+cos(2x),x∈(-∞,+∞);是|y|≤12-1+1=2.4 10.11.12.(6)y=x2sinx,x∈(-∞,+∞);否.(7)y=x2cosx,x∈(-1010,1010).是13.证明函数y=1+x-x在(1,+∞)内是有界函数.证y=1+x-x=(1+x-x)(1+x+x)1+x+x=11+x+x<12+1(x>1).13.研究函数y=x6+x4+x21+x6在(-∞,+∞)内是否有界.|x|≤1时,x6+x4+x2x6+x4+x23x6解1+x6≤3,|x|>1时,1+x6≤x6=3,|y|=y≤3,x∈(-∞,+∞).5第二篇：北大版高等数学第一章函数及极限答案习题1.4 习题1.41.直接用ε-δ说法证明下列各极限等式:(1)limx→ax=a(a>0);(2)limx=a;(3)lime=e;(4)limcosx=cosa.x→ax→ax→a22xa证(1)∀ε>0,要使||x-a|x-a|=|x-a|x-a<ε,由于|x-a|x+a<|x-a|ax-,a|<ε,故lim只需<ε,|x-a|<aε.取δ=aε,则当|x-a|<δ时,|x=a.ax→a(2)∀ε>0,不妨设|x-a|<1.要使|x2-a2|=|x+a||x-a|<ε,由于|x+a|≤|x-a|+|2a|<1+|2a|,只需(1+|2a|)|x-a|<ε,|x-a|<ε当1+|2a|.取δ=min{ε1+|2a|,1},则|x-a|<δ时,|x2-a2|<ε,故limx2=a2.x→a(3)∀ε>0,设x>a.要使|ex-ea|=ea(ex-a-1)<ε,即0<(ex-a-1)<εea,1<ex-a<1+εea,0<x-a<ln⎛ε⎫=min{ε1+,1},则当0<x-a<δ时,|ex-eaa⎪,取δ|<⎝e+|2a|ε,⎭1故limex=ea.类似证limex=ea.故limex=ea.x→a+x→a-x→a(4)∀ε>0,要使|cosx-cosa|=2sinx+aa2sinx-a2=2sinx+a2sinx-2≤|x-a|,取δ=ε,则当|x-a|<δ时,|cosx-cosa|<ε,故limcosx=cosa.x→a2.设limf(x)=l,证明存在a的一个空心邻域(a-δ,a)⋃(a,a+δ),使得函数u=f(x)在x→a该邻域内使有界函数.证对于ε=1,存在δ>0,使得当0<|x-a|<δ时,|f(x)-l|<1,从而|f(x)|=|f(x)-l+l|≤|f(x)-l|+|l|<1+|l|=M.3.求下列极限:2(1)lim(1+x)2-1=lim2x+x=lim(1+x1.x→02xx→02xx→02)=22sin2⎛x⎛⎫(2)lim1-cosx⎝2⎪⎭=1 sin⎛x ⎫⎫⎪⎪1x→0x2=limx→0x22lim ⎝2⎭⎪=γ12 =1.x→0 x ⎪22⎝2⎪⎭(3)limx+a-axx=lim=1(a>0).x→0x→0x(x+a+a)2a(4) limx2-x-2x→12x2-2x-3=-2-3.x2(5)lim-x-2-2x→02x2-2x-3=-3.1 201030(6)lim(2x-3)(2x+2)x→∞(2x+1)30=2230=1.(7)lim1+x-1-x=lim2x=1.x→0xx→0x(1+x+1-x)(8)lim⎛13⎫x2-x+1-3x2-x-2x→-1 -⎝x+1x3+1⎪=lim⎭x→-1(x+1)(x2-x+1)=limx→-1(x+1)(x2-x+1)=lim(x+ 1)(x-2)(x-2)=-3x→-1(x+1)(x2-x+1)=limx→-1(x2-x+1)3=-1.(9)lim1 +2x-3=lim(1+2x-3)(x+2)(1+2x+3)x→4x-2x→4(x-2)(x+2)(1+2x+3)=li m(2x-8)(x+2)=2γ4x→4(x-4)(1+2x+3)6=43.n(n-1)2nlimxn-1n(10)-1ny+2y+Λ+yx-1=lim(1+y)x→1y→0y=lim=n.y→0y(11)limx2+1-x2-1)=lim2=0.x→∞(x→∞x2+1+x2-1mm-1(12)lima0x+a1x+Λ+amamx →0bnn-10x+b+Λ+b(bn≠0)=1xnb.n-1⎧a0/b0,m=n(13)lima0xm+a1 xm+Λ+amx→∞bnbn-1+Λ+b(aγb⎪00≠0)=⎨0, n>m0x+1xn⎪⎩∞, m>n.x4+81+8/x4(14)limx+11+1/x2=1.x→∞2=limx→∞31+3x-3(15)li m1-2xx→0x+x2(3221+3x-333=lim1-2x)(1+3x+1+3xγ31-2x+31-2x )x→0x+x2)(321+3x+31+3xγ31-2x+32(1-2x)=lim5xx→0x(1+x)(321+ 3x+321+3xγ31-2x+31-2x)=lim522=5x→0(1+x)(31+3x+31+3xγ31-2x+31-2x)3.(16)a>0,li mx-a+x-a=lim⎛x-a1⎫x→a+0x2-a2x→a+0 ⎝x2-a2+x+a⎪⎪⎭=lim⎛(x-a) (x+a)+1⎫x→a+0 ⎝x+ax-a(x+a)x+a⎪⎪⎭2=lim⎛(x-a)+1⎫x→a+0 ⎝x+ax-a(x+a)x+a⎪⎭=lim⎛x-a+1⎫1.x→a+0 ⎝x+a(x+a)x+a⎪⎪=⎭2ax4.利用limsinx=1及lim⎛1x→xx→∞1+⎫⎝x⎪=e求下列极限:⎭(1)limsinαxsinαxαx→0tanβx=limx→0sinβxlimcosβx=x→0β.sin( 2x2)sin(2x2(2)lim)2x2x→3x=lim1γ0=0x→02x2γlimx→03x=(3)limta n3x-sin2x=limtan3xsin2x21x→0sin5xx→0sin5x-limx→0sin5x=35 -5=5.(4)limx=limxx→0+1-cosxx→0+2sinx=2.2cosx+aa(5)limsinx-s ina2sinx-2=cosa.x→ax-a=limx→ax-a2-k⎛k⎫-xx(-k)⎡x(6)limlimk=⎢⎛k⎫k⎤=e-k.∞1+x→⎝x⎪⎭x→∞1+⎫k=⎛⎝x⎪⎭⎢limx→∞1+⎪⎥⎣⎝x⎭⎥⎦-5(7)lim(1 -5y)1/y=⎡1/(5y)⎤-5y→0⎢⎣lim(1-5y)⎥=e.y→0⎦x+100x10(8)lim⎛1+10= lim⎛1+1=e.x→∞⎫⎝x⎪⎭x→∞⎫⎡⎛1⎫⎤⎝x⎪⎭⎢lim⎣x→∞1+⎝x⎪⎭⎥⎦5.给出limf(x)=+∞及limf(x)=-∞的严格定义.x→ax→-∞limf(x)=+∞:对于任意给定的A>0,存在δ>0,使得当0<|x-a|<δ时f(x)>A.x→alimf(x)=-∞:对于任意给定的A>0,存在∆>0,使得当x<-∆时f(x)<-A.x→-∞3第三篇：北大版高等数学第一章函数及极限答案习题1.6 习题1.61.证明:任一奇数次实系数多项式至少有一实根.证设P(x)是一奇数次实系数多项式,不妨设首项系数是正数,则limP(x)=+∞,x→+∞limP(x)=-∞,存在A,B,A<B,P(A)<0,P(B)>0,P在[A,B]连续,根据连续函数x→-∞的中间值定理,存在x0∈(A,B),使得P(x0)=0.2.设0<ε<1,证明对于任意一个y0∈R,方程y0=x-εsinx有解,且解是唯一的.证令f(x)=x-εsinx,f(-|y0|-1)=-|y0|-1+ε<-|y0|≤y0,f(|y0|+1)≥|y0|+1-ε>|y0|≥y0,f在[-|y0|-1,|y0|+1]连续,由中间值定理,存在x0∈[-|y0|-1,|y0|+1],f(x0)=y0.设x2>x1,f(x2)-f(x1)=x2-x1-ε(sinx2-sinx1)≥x2-x1-ε|x2-x1|>0,故解唯一.3.设f(x)在(a,b)连续,又设x1,x2∈(a,b),m1>0,m2>0,证明存在ξ∈(a,b)使得f(ξ)=m1f(x1)+m2f(x2)m1+m2.证如果f(x1)=f(x2),取ξ=x1即可.设f(x1)<f(x2),则f(x1)=m1f(x1)+m2f(x1)m1+m2≤m1f(x1)+m2f(x2)m1+m2≤m1f(x2)+m2f(x2)m1+m2=f(x2),在[x1,x2]上利用连续函数的中间值定理即可.4.设y=f(x)在[0,1]上连续且0≤f(x)≤1,∀x∈[0,1].证明在存在一点t∈[0,1]使得f(t)=t.证g(t)=f(t)-t,g(0)=f(0)≥0,g(1)=f(1)-1≤0.如果有一个等号成立,取t为0或1.如果等号都不成立,则由连续函数的中间值定理,存在t∈(0,1),使得g(t)=0,即f(t)=t.5.设y=f(x)在[0,2]上连续,且f(0)=f(2).证明在[0,2]存在两点x1与x2,使得|x1-x2|=1,且f(x1)=f(x2).证令g(x)=f(x+1)-f(x),x∈[0,1].g(0)=f(1)-f(0),g(1)=f(2)-f(1)=f(0)-f(1)=-g(0 ).如果g(0)=0,则f(1)=f(0),取x1=0,x2=1.如果g(0)≠0,则g(0),g(1)异号,由连续函数的中间值定理,存在ξ∈(0,1)使得g(ξ)=f(ξ+1)-f(ξ)=0,取x1=ξ,x2=ξ+1.第四篇：北大版高等数学第一章函数及极限答案习题1.3习题1.31.设xn=nn+2(n=1,2,Λ),证明limxn=1,即对于任意ε>0,求出正整数N,使得n→∞当n>N时有 |xn-1|<ε,并填下表:n-1|=2n+2<ε,只需n>2-2,取证∀ε>0,不妨设ε<1,要使|xn-1|=|N=n+2ε⎡2⎤-2,则当n>N时,就有|xn-1|<ε.⎢ε⎥⎣⎦n→∞n→∞2.设liman=l,证明lim|an|=|l|.证∀ε>0,∃N,使得当n>N时,|an-l|<ε,此时||an|-|l||≤|an-l|<ε,故lim|an|=|l|.n→∞3.设{an}有极限l,证明(1)存在一个自然数N,n<N|an|<|l|+1;(2){an}是一个有界数列,即存在一个常数M,使得|an|≤M(n=12,Λ).证(1)对于ε=1,∃N,使得当n>N时,|an-l|<1,此时|an|=|an-l+l|≤|an-l|+|l|<|l|+1.(2)令M=max{|l|+1,|a1|,Λ,|aN|},则|an|≤M(n=12,Λ).4.用ε-N说法证明下列各极限式:(1)limn→∞3n+12n-3=;(2)limn→∞n+1=0;(3)limnq=0(|q|<1);(4)limn→∞n→∞2nn!nn=0;⎛1⎫11(5)lim ++Λ+⎪=1;n→∞1γ22γ3(n-1)γn⎝⎭⎛⎫11(6)lim +Λ+=0.3/ 23/2⎪n→∞(n+1)(2n)⎝⎭证(1)∀ε>0,不妨设ε<1,要使3n+12n-3-32=112(2n-3)<ε,只需n>112ε+3,取N=3n+133n+13⎡11⎤+3,当n>N时,-<ε,故lim=.⎢2ε⎥n→∞2n-32n-322⎣⎦(2)∀ε>0,要使<ε,由于≤只需<ε,n>ε3,⎡1取N=⎢ε3⎣(3)|q|=|nq|=n⎤,当n>N时⎥⎦1<ε.1+αn(α>0).n>4=1+nα+<124nαnn(n-1)(1+α)6nnα+n(n-1)(n-2)α+Λ+α⎤}.⎥⎦3n<(n-1)(n-2)αn!nn<ε,n>⎡1⎢ε⎣⎤.⎥⎦εα,N=max{4,⎡24⎢εα3⎣(4)≤1n<ε,n>ε,N=⎛1⎫11(5) ++Λ+⎪-1(n-1)γn⎭⎝1γ22γ3⎛⎛11⎫⎛11⎫⎛11⎫⎫11⎡1=-⎪+-⎪+Λ+-⎪⎪-1=<ε,n>,N=⎢nε⎣ε⎝(n-1)n⎭⎭⎝⎝12⎭⎝23⎭⎤.⎥⎦1(n+1)n→∞3/2+Λ+1(2n)3/2≤n(n+1)3/2<<ε,n>ε,N=⎡1⎢ε2⎣⎤.⎥⎦5.设liman=0,{bn}是有界数列,即存在常数M,使得|bn|<M(n=1,2,Λ),证明limanbn=0.n→∞证∀ε>0,∃正整数 N,使得|an|<故limanbn=0.n→∞εM,|anbn|=|an||bn|≤εMγM=ε,6.证明limn→∞=1.证∀ε>0,要使1|n(1+ε)n1<ε,只需n(1+ε)n<1.4nε1+nε+nn(n-1)<ε(n-1)ε<4nε,只需<1,n>ε,N=⎡4⎢ε2⎣⎤.⎥⎦7.求下列各极限的值:(1)limn→∞=limn→∞=0.22(2)limn→∞n+3n-1004n-n+2(2n+10)n+n =limn→∞1+3/n-100/n4-1/n+2/n=.(3)limn→∞=limn→∞(2+10/n)1+1/nn=16.-21⎫⎛(4)lim 1+⎪n→∞n⎭⎝-2n⎡1⎫⎤⎛=⎢lim 1+⎪⎥n→∞n⎭⎥⎝⎢⎣⎦=e.-21⎫1⎛(5)lim 1-⎪=limn-1n→∞n→∞n⎭⎝1⎫⎛1⎫⎛1+1+⎪⎪n-1⎭⎝n-1⎭⎝=1⎫⎛lim 1+⎪n→∞n-1⎭⎝1⎫⎛(6)lim 1-⎪n→∞n⎭⎝nnnn-1=1⎫⎛lim 1+⎪n→∞n-1⎭⎝nn1e.⎡⎛1⎫⎤11⎫⎛=lim⎢1-⎪⎥,取q∈(,1),∃N,当n>N时, 1-⎪<qn→∞n⎭⎥en⎭⎝⎢⎣⎝⎦⎡⎛1⎫⎤1⎫⎛1-=0,即lim1-⎢⎥⎪⎪n→∞nn⎝⎭⎝⎭⎢⎥⎣⎦nnnnn⎡⎛1⎫⎤nn0<⎢1-⎪⎥<q,limq=0,limn→∞n→∞n⎭⎥⎢⎣⎝⎦nnn=0.1⎫1⎫1⎫1⎛⎛⎛(7)lim 1-2⎪=lim 1+⎪lim 1-⎪=e=1.n→∞n→∞n⎭n⎭n→∞⎝n⎭e⎝⎝8.利用单调有界序列有极限证明下列序列极限的存在性:(1)xn=xn<1+(2)xn=11+11γ212+1+Λ+1n,xn+1=xn+=2-12+1n1(n+1)>xn,+Λ+1(n-1)n11n<2.xn单调增加有上界，故有极限.,xn+1=xn+n+1+2+1+Λ++1>xn,1-n1111⎛111⎫1<1.xn=+2+Λ+n=1++2+Λ+n-1⎪=2222⎝222⎭21-12xn单调增加有上界，故有极限.(3)xn=1n+1+1n+2+Λ+1n+n.xn+1-xn=12n+2-1n+1=-12n+2<0,xn+1<xn,xn>0,xn单调减少有下界，故有极限.(4)xn=1+1+12!+Λ+1n!.xn+1-xn=1(n+1)!>0,1⎫⎛11⎫1⎫1⎛⎛1xn≤2+1-⎪+-⎪+Λ+-⎪=3-<3.2⎭⎝23⎭n⎝⎝n-1n⎭xn单调增加有上界，故有极限.11⎫⎛9.证明e=lim 1+1++Λ+⎪.n→∞2!n!⎭⎝1⎫1n(n-1)1n(n-1)Λ(n-k+1)1⎛证 1+⎪=1+n+2+Λ++knn2!nk!n⎝⎭Λ+n(n-1)Λ(n-n+1)1n!nnn=2+1⎛1⎫1⎛1⎫⎛k-1⎫1⎛1⎫⎛n-1⎫1-+1-Λ1-+1-Λ1-⎪⎪⎪⎪⎪2!⎝n⎭k!⎝n⎭⎝n⎭n!⎝n⎭⎝n⎭1n1⎫11⎫⎛⎛<1+1++Λ+.e=lim 1+⎪≤lim 1+1++Λ+⎪.n→∞n→∞2!n!n⎭2!n !⎭⎝⎝对于固定的正整数k,由上式,当n>k 时,1⎫1⎛1⎫1⎛1⎫⎛k-1⎫⎛1+>2+1-+1-Λ1-⎪⎪⎪⎪,n⎭2!⎝n⎭k!⎝n⎭⎝n⎭⎝11⎫⎛令n→∞得e≥1+1++Λ+⎪,2!k!⎝⎭11⎫11⎫⎛⎛e≥lim 1+1++Λ+=lim1+1++Λ+⎪n→∞⎪.k→∞2!k!2!n!⎝⎭⎝⎭10.设满足下列条件:|xn+1|≤k|xn|,n=1,2,Λ,其中是小于1的正数.证明limxn=0.n→∞nn-1证由|xn+1|≤k|xn|≤k|xn-1|≤Λk|x1|→0(n→∞),得limxn=0.n→∞第五篇：北大版高等数学第一章函数及极限答案习题1.5 习题1.5 1.试用ε-δ说法证明(1)1+x在x=0连续(2)sin5x在任意一点x=a连续.证(1)∀ε>0,要使|x<ε,|x|<221+x-21+0|=2x22<ε.由于22x22≤x,只需221+x+11+x+11+0|<ε,故1+x在x=0连续.5(x-a)2|<ε.ε,取δ=ε,则当|x|<δ时有|1+x-5x+5a2||sin(2)(1)∀ε>0,要使|sin5x-sin5a|=2|cos由于2|cos取δ=5x+5a2||sin5(x-a)2|≤5|x-a|,只需5|x-a|<ε,|x-a|<ε5,ε5,则当|x-a|<δ时有|sin5x-sin5a|<ε,故sin5x在任意一点x=a连续.2.设y=f(x)在x0处连续且f(x0)>0,证明存在δ>0使得当|x-x0|<δ时f(x)>0.证由于f(x)在x0处连续,对于ε=f(x0)/2,存在存在δ>0使得当|x-x0|<δ时f(x)-f(x0)|<f(x0)/2, 于是f(x)>f(x0)-f(x0)/2=f(x0)/2>0.3.设f(x)在(a,b)上连续,证明|f(x)|在(a,b)上也连续,并且问其逆命题是否成立?证任取x0∈(a,b),f在x0连续.任给ε>0,存在δ>0使得当|x-x0|<δ时|f(x)-f(x0)|<ε,此时||f(x)|-|f(x0)||≤|f(x)-f(x0)|<ε,故|f|在x0连续.其逆命题⎧1,x是有理数不真,例如f(x)=⎨处处不连续,但是|f(x)|≡1处处连续.⎩-1,x是无理数4.适当地选取a,使下列函数处处连续: 2⎧⎧ln(1+x), x≥1,⎪1+x,x<0,(1)f(x)=⎨(2)f(x)=⎨⎩aarccosπx,x<1.⎪⎩a+x x≥0;解(1)limf(x)=limx→0-x→0-x→1+x→1+1+x2=1=f(0),limf(x)=f(0)=a=1.x →0+x→1-x→1-(2)limf(x)=limln(1+x)=ln2=f(1),limf(x)=limaarccosπx=-a=f(1)=ln2,a=-ln2.5.利用初等函数的连续性及定理3求下列极限:(1)limcosx→+∞1+x-x=22x=coslimx→+∞1+x-xx=cos0=1.(2)limxx →2x.sin2xsin3x2sin2x(3)limex→0sin3x=elimx→0=e3.=arctanlimx →∞(4)limarctanx→∞x+8x+124x+8x+124=arctan1=π4.1(5)limx→∞( x+1-3|x|x+1+22x-2)|x|=⎤⎥=2x-2⎦x→x02lim⎡(x→∞⎣x+1-22x-2)|x|⎤⎦=⎡lim⎢x→∞⎣x→x0⎡⎤3lim⎢⎥=22x→∞⎣1+1/x+1-2/x⎦g(x)32.6.设limf(x)=a>0,limg(x)=b,证明lim)f(x)x→x0lim[(lnf(x))g(x)]=a.=a.bb证lim)f(x)x→x0g(x)=lim)ex→x0(lnf(x))g(x)=ex→x0=eblna7.指出下列函数的间断点及其类型,若是可去间断点,请修改函数在该点的函数值,使之称为连续函数:(1)f(x)=cosπ(x-[x]),间断点n∈Z,第一类间断点.(2)f(x)=sgn(sinx),间断点nπ,n∈Z,第一类间断点.⎧x,x≠1,(3)f(x)=⎨间断点x=1,第一类间断点.⎩1/2,x=1.⎧x+1,0≤x≤1⎪(4)f(x)=⎨间断点x=1,第二类间断点.π,1<x≤2,⎪sinx-1⎩⎧1,0≤x≤1,⎪2-x⎪(5)f(x)=⎨x,1<x≤2,间断点x=2,第一类间断点.⎪1⎪,2<x≤3.⎩1-x228.设y=f(x)在R上是连续函数,而y=g(x)在R上有定义,但在一点x0处间断.问函数h(x)=f(x)+g(x)及ϕ(x)=f(x)g(x)在x0点是否一定间断?解h(x)=f(x)+g(x)在x0点一定间断.因为如果它在x0点连续,g(x)=(f(x)+g(x))-f(x)将在x0点连续,矛盾.而ϕ(x)=f(x)g(x)在x0点未必间断.例如f(x)≡0,g(x)=D(x).。

习题1.1222222222222222222.,,.3,3.3,,313 2.961,9124,31.3,93,3,3.,,.,,,,p p p q p q p q q p p k p k p k k p k k p p k k q q k q p q p a a a b p a pb b b====+=+=++=++======为互素自然数除尽必除尽否则或除将余故类似得除尽与互素矛盾.设是正的素数为互素自然数,则素证 2.证 1.2222222,,.,..,:(1)|||1| 3.\;(2)|3| 2.0,13,22,1,(1,0);01,13,13,(0,1);1,13,3/2,(1,3/2).(1,0)(0,1)p a p a a pk p k pb pk b p b a b x x x x x x x x x x x x x x x X ===+-<-<<-+-<>->--<<+-<<>+-<<=-⋃数除尽故除尽类似得除尽此与为互素自然数矛盾.解下列不等式若则若则若则3.解(1)222(1,3/2).(2)232,15,1||5,1||(1).,(1)||||||;(2)||1,|||| 1.(1)|||()|||||||||,||||||.(2)|||()||||||x x x x x a b a b a b a b a b a a b b a b b a b b a b a b a b a b b a b b ⋃-<-<<<<<<<=⋃-+≥--<<+=++-≤++-=+++≥-=+-≤+-<设为任意实数证明设证明证4.,| 1.(1)|6|0.1;(2)||.60.160.1. 5.9 6.1.(, 6.1)( 5.9,).(2)0,(,)(,);0,;0,(,).11,01,.1, 1.11x x a l x x x x X l X a l a l l x a l X a a n n a b a ++>->+>+<->-<-=-∞-⋃-+∞>=++∞⋃-∞-=≠<=-∞+∞-><<>=>-=-=解下列不等式或或若若若若证明其中为自然数若解(1)证5.:6.1200001)(1)1).(,),(,).1/10.{|}.(,),,{|},10{|}./10,(1)/10,/10(1)/101/10n n n n n n n n n n n b b n a b a b n b a mA A m A a b ABC B A x x b C A x x a B m m C b a m m --+++><-=∈⋂=∅=⋃=⋂≥=⋂≤-∈-≤-Z 设为任意一个开区间证明中必有有理数取自然数 满足考虑有理数集合= 若则中有最小数-=证7.(,),(,).1/10.|}.10n n nn a b a b mn b a A m <-=∈Z ,此与的选取矛盾. 设为任意一个开区间证明中必有无理数取自然数 满足考虑无理数集合 以下仿8题.8.证习题1.26426642642666613.(1,)1).13.(,).13||13,||1,3,11||3,(,).yy xx x xyxx x x x x x xx xx x xy y x=+∞===<>++=-∞+∞+++++≤≤>≤=++=≤∈-∞+∞证明函数内是有界函数.研究函数在内是否有界时,时证解习题1.4221.-(1)0);(2)lim;(3)lim;(4)lim cos cos.1)0,|,,||.,||,|,(2)0x ax a x a x a x ax aa x a e e x ax a x aεδεεεδδεε→→→→→=>===∀>=<<<-<=-<<=∀>直接用说法证明下列各极限等式:要使取则当时故证(222222,|| 1.||||||,|||||2|1|2|,1|2|)||,||.min{,1},||,1|2|1|2|||,lim(3)0,.||(1),01),1x ax a a x a x aax a x a x a x ax a x a a aa x a x a x aa ax a x ax a e e e e eeεεεεδδεεεε→---<-=+-<+≤-+<++-<-<=-<++-<=∀>>-=-<<-<<不妨设要使由于只需(取则当时故设要使即(.1,0ln1,min{,1},0,||,1|2|lim lim lim0,|cos cos|2sin sin2sin sin||,2222,|,|cos cosx aax aax a x a x ax a x a x aeex a x a e ee ae e e e e ex a x a x a x ax a x a x a x aεεεδδεεδεδ-→+→-→<+⎛⎫<-<+=<-<-<⎪+⎝⎭===+-+-∀>-==≤-=-<-取则当时故类似证故要使取则当|时...(4)2|,lim cos cos.2.lim(),(,)(,),().1,0,0|-|,|()|1,|()||()||()|||1||.(1)1(1)lim lim2x ax ax xx af x l a a a a a u f xx a f x lf x f x l l f x l l l Mxxεδδεδδ→→→→<==-⋃+==><<-<=-+≤-+<+=+-=故设证明存在的一个空心邻域使得函数在该邻域内使有界函数对于存在使得当 时从而求下列极限证3.:2002222200000221222lim(1) 1.222sin sin1cos11122(2)lim lim lim1.2222(3)0).22(4)lim.22332(5)lim22xx x xx xxxx x xxx xxxx xax xx xx xx x→→→→→→→→+=+=⎛⎫⎛⎫⎛⎫⎪ ⎪⎪-⎝⎭⎝⎭⎪====⎪⎪⎝⎭==>---=-------2.33-=-20103030300022********(23)(22)2(6)lim 1.(21)2 1.13132(8)lim lim lim 11(1)(1)(1)(1)(1)(2)lim lim (1)(1)x x x x x x x x x x x x x x x x x x x x x x x x x x x x →∞→→→-→-→-→--+==+==-+---⎛⎫-== ⎪+++-++-+⎝⎭+-==+-+214442100(2)31.(1)3244.63(1)1(1)12(10)lim lim lim .1(11)lim x x x nnnx y y x x x x n n ny y y x y n x y y→-→→→→→→→∞--==--+====-+++-+-===-1011001001010010120.(12)lim (0)./,(13)lim(0)0, , .(14)lim lim 1x m m m mnn n x n n m m m n nx nx x a x a x a a b b x b x b b a b m na x a x a ab n m b xb x b m n x --→--→∞→∞→∞==+++≠=+++=⎧+++⎪≠=>⎨+++⎪∞>⎩=+21.11/x =+033233223220312(1212)5lim(112)55lim .3(112)(16)0,l x x x xx x x x x x xx x x x x x a →→→→-+=+-+-=++-+==++-+>00im lim lim x a x a x a →+→+→+⎛⎫=⎛⎫=00lim lim x a x a →+→+⎛⎫=⎫==000222200000sin 14.lim 1lim 1sin sin (1)limlim lim cos .tan sin sin(2)sin(2)2(2)lim lim lim 100323tan 3sin 2tan 3sin 2(3)lim lim lim sin 5sin 5xx x x x x x x x x x x x e x x x x x x x x x x x x xx x x x x αααββββ→→∞→→→→→→→→→⎛⎫=+= ⎪⎝⎭=====-=-利用及求下列极限:00()1/0321.sin 5555(4)lim lim 2cos sinsin sin 22(5)lim lim cos .2(6)lim 1lim 1lim 1.(7)lim(15)x x x a x a kxxxk kk k x x x yy x x xxx a x a x a a x a x ak k k e x x x y →→+→→----→∞→∞→∞→=-===+--==--⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥+=+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦-=51/(5)50100100lim(15).111(8)lim 1lim 1lim 1.5.lim ()lim ().lim ():0,0,0|-|().lim (y y x xx x x x ax x a x y e e x x x f x f x f x A x a f x A f x δδ--→+→∞→∞→∞→→-∞→→-∞⎡⎤-=⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫⎛⎫+=++= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦=+∞=-∞=+∞>><<>给出及的严格定义对于任意给定的存在使得当时):0,0,().A x f x A =-∞>∆><-∆<-对于任意给定的存在使得当时习题1.5222 21.(2)sin5.(1)0,|.,,|||||,0555()(2)(1)0,|sin5sin5|2|cos||sin|.22xx x axx x x xx a x ax aεδεεεδδεεε-==∀>=<≤<<=<<=+-∀>-=<试用说法证明连续在任意一点连续要使只需取则当时有连续.要使由于证000000555()2|cos||sin|5||,5||,||,225,|||sin5sin5|,sin55()()0,0||()0.(),()/2,0||(x a x ax a x a x ax a x a x x a y f x x f x x x f xf x x f x x xf xεεεδδεδδεδδ+-≤--<-<=-<-<==>>-<>=>-<只需取则当时有故在任意一点连续.2.设在处连续且证明存在使得当时由于在处连续对于存在存在使得当时证000000000000 )()|()/2,()()()/2()/20.3.()(,),|()|(,),?(,),.0,0|||()()|,||()||()|||()()|,||.f x f x f x f x f x f xf x a b f x a bx a b f x x xf x f x f x f x f x f x f xεδδεε-<>-=>∈>>-<-<-≤-<于是设在上连续证明在上也连续并且问其逆命题是否成立任取在连续任给存在使得当时此时故在连续其证0001,,(),()|11,ln(1),1,0,(1)()(2)()arccos, 1.0;lim()lim1(0),lim()(0)x x xxf x f xxax xxf x f xa x xa x xf x f f x fπ→-→→+⎧=≡⎨-⎩+≥⎧<==⎨<+≥⎩⎪⎩=====逆命题是有理数不真例如处处不连续但是|处处连续.是无理数4.适当地选取,使下列函数处处连续:解(1)11112sin2limsin31.(2)lim()lim ln(1)ln2(1),lim()lim arccos(1)ln2,ln2.5.3:(1)lim cos lim cos0 1.(2)lim(3)lim xx x x xx xxxxxaf x x f f x a x a fae eπ→→+→+→-→-→+∞→+∞→→==+====-===-=====利用初等函数的连续性及定理求下列极限sin22sin33.(4)lim arctan arctan1.4xxx xeπ→∞→∞====()()(ln ())()(5)6.lim ()0,lim (),lim)().lim)()lim)x g x b x x x x x x g x f x g x x x x x f x a g x b f x a f x e →→→→→=====>====设证明证0lim [(ln ())()]ln 22.7.,,(1)()cos ([]),,(2)()sgn(sin ),,,,1,(3)()1,1/2, 1.1(4)()x x f x g x b a b e e a f x x x n f x x n n x x f x x x x f x ππ→===-∈=∈⎧≠==⎨=⎩+=Z Z 指出下列函数的间断点及其类型若是可去间断点请修改函数在该点的函数值,使之称为连续函数:间断点第一类间断点.间断点第一类间断点.间断点第一类间断点.,011,sin,12,11,01,2(5)(),12,2,1,2 3.1x x x x x x f x x x x x xπ⎧≤≤⎪=⎨<≤⎪-⎩⎧≤≤⎪-⎪=<≤=⎨⎪⎪<≤-⎩间断点第二类间断点.间断点第一类间断点.0000008.(),(),()()()()()()()()()()(()())()()()()()0,()().y f x y g x x h x f x g x x f x g x x h x f x g x x x g x f x g x f x x x f x g x x f x g x D x ϕϕ===+==+=+-=≡=R R 设在上是连续函数而在上有定义但在一点处间断.问函数及在点是否一定间断?在点一定间断.因为如果它在点连续,将在点连续,矛盾.而在点未必间断.例如解习题1.600001.:()lim (),lim (),,,,()0,()0,[,],,(,),()0.2.01,,sin ,.(x x P x P x P x A B A B P A P B P A B x A B P x y y x x f x εε→+∞→-∞=+∞=-∞<<>∈=<<∈=-R 证明任一奇数次实系数多项式至少有一实根.设是一奇数次实系数多项式,不妨设首项系数是正数,则存在在连续根据连续函数的中间值定理存在使得设证明对于任意一个方程有解且解是唯一的令证证000000000000000212121212121)sin ,(||1)||1||,(||1)||1||,[||1,||1],,[||1,||1],().,()()(sin sin )||0,.3.()(,x x f y y y y f y y y y f y y x y y f x y x x f x f x x x x x x x x x f x a b εεεεε=---=--+<-≤+≥+->≥--+∈--+=>-=---≥--->在连续由中间值定理存在设故解唯一设在1212112212121121121112212221212121212),,(,),0,0,(,)()()().()(),.()(),()()()()()()()(),[,]x x a b m m a b m f x m f x f m m f x f x x f x f x m f x m f x m f x m f x m f x m f x f x f x m m m m m m x x ξξξ∈>>∈+=+==<+++=≤≤=+++连续又设证明存在使得如果取即可设则在上利用连续函数的中间值定理证.4.()[0,1]0()1,[0,1].[0,1]().()(),(0)(0)0,(1)(1)10.,01.,,(0,1),()0,().5.()[0,2],(0)(2).y f x f x x t f t t g t f t t g f g f t t g t f t t y f x f f =≤≤∀∈∈==-=≥=-≤∈====即可设在上连续且证明在存在一点使得如果有一个等号成立取为或如果等号都不成立则由连续函数的中间值定理存在使得即设在上连续且证明证12121212[0,2],||1,()().()(1)(),[0,1].(0)(1)(0),(1)(2)(1)(0)(1)(0).(0)0,(1)(0),0, 1.(0)0,(0),(1),,(0,1)()(1x x x x f x f x g x f x f x x g f f g f f f f g g f f x x g g g g f ξξξ-===+-∈=-=-=-=-====≠∈=+在存在两点与使得且令如果则取如果则异号由连续函数的中间值定理存在使得证12)()0,, 1.f x x ξξξ-===+取第一章总练习题221.:581 2.3|58|1422.|58|6,586586,.3552(2)33,52333,015.5(3)|1||2|1(1)(2),2144,.22|2|,.2,2,4,2;2,3x x x x x x x x x x x x x x x x x y x x x y x y x y x y x y x -≥-≥-≥-≥-≤-≥≤-≤-≤-≤≤≤+≥-+≥-+≥-+≥=+-≤=+≤=->=求解下列不等式（）或或设试将表示成的函数当时当时解解解2.解222312312,4,(2).32,41(2), 4.313.1.22,4(1)44,0.1,0.4.:1232(1)2.222221211,.22123222n n y x y y y x y y x x x x x x x x x x n n n n ->=--≤⎧⎪=⎨->⎪⎩<+≥-<++<++>≥-≠+++++=-+==++的全部用数学归纳法证明下列等式当时,2-等式成立设等式对于成立,则解证1231111121211222112312222222124(1)(1)3222,22221..1(1)(2)123(1).(1)1(11)1(1)1,(1)(1)n n n n n n n n n n n n n n n n n n n n n x nx x x nxx x x x x n x x ++++++-+++++=++++++++-+++=-+=-=-+-++++++=≠--++-===--即等式对于也成立故等式对于任意正整数皆成立当时证1,1212.1(1)123(1)(1)(1)n n n nnn n x nx x x nxn x n xx +--++++++++=++-等式成立设等式对于成立,则122122112211221221(1)(1)(1)(1)1(1)(12)(1)(1)1(1)(2)(1)(1)1(1)(2)(1)(1)1(2)(1),(1)1n n n n n n n n n n n n n n n n n n n x nx x n x x n x nx x x n x x n x nx x x x n x n x nx x x x n x n x n x x n ++++++++++-+++-+=--+++-++=--+++-++=--+++-++=--+++=-+即等式对于成立.,.|2|||25.()(1)(4),(1),(2),(2);(2)();(3)0()(4)224211222422(1)(4)1,(1)2,(2)2,(2)0.41224/,2(2)()x x f x xf f f f f x x f x x f f f f x x f x +--=---→→----------==--==-====----≤-=由归纳原理等式对于所有正整数都成立设求的值将表成分段函数当时是否有极限:当时是否有极限?解00022222222;2,20;0,0.(3).lim ()2,lim ()0lim ().(4).lim ()lim (4/)2,lim ()lim 22lim (),lim () 2.6.()[14],()14(1)(0),x x x x x x x x x x x f x f x f x f x x f x f x f x f x x f x x f →-→+→-→--→--→-+→-+→--→-⎧⎪-<≤⎨⎪>⎩==≠=-======--无因为有设即是不超过的最大整数.求003,;2(2)()0?(3)()?391(1)(0)[14]14,1467.[12]12.244(2).lim ()lim[14]14(0).(3).()12,()x y x x f f f x x f x x f f f f x y f f x f x →→+⎛⎫⎪⎝⎭==⎛⎫⎡⎤⎡⎤=-=-=-=-+=-=-=- ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦=-=-==-的值在处是否连续在连续因为不连续因为解111111.7.,0,,:(1)(1);(2)(1).n n n n n n a b a b n b a b a n b n a b a b a++++=-≤<--<++<--设两常数满足对一切自然数证明1111111()()(1),(1).118.1,2,3,,1,1.:{},{}..111,1,7,111n n n n n n n n n n n n nn n n n n n n b a b a b b a a b b b b n b b a b a b a n a b an a b n n a b a b a b n nn ++--+++--+++=<+++=+--->+-⎛⎫⎛⎫==+=+ ⎪ ⎪⎝⎭⎝⎭<+=++⎛+ ⎝类似有对令证明序列单调上升而序列单调下降,并且令则由题中的不等式证证=11111111111(1)1,111111111(1)11(1)1111111,11111.1111(1)11n n nn n nn nn nn n n n n n n n n n n n n n n n n n n n n n +++++++⎫⎛⎫-+⎪ ⎪+⎛⎫⎭⎝⎭<++ ⎪⎝⎭-+⎛⎫⎛⎫⎛⎫+-+<++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+-+<+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫+<+ ⎪ ⎪+⎝⎭⎝⎭⎛⎫+ ⎛⎫⎝⎭++< ⎪+⎝⎭111111121111111111(1)1111(1)11111111111111111.1111111.111n n nn n nn n n n n n n n n n n n n n n n n n nn n n n n +++++++⎛⎫-+⎪ ⎪+⎝⎭-+⎛⎫⎛⎫⎛⎫++<+-+ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+<+-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+++<+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫++>+ ⎪++⎝⎭⇔我们证明22111211111(1)11..(1)(1)1111,1,1,11.nn n n n n n n n n n n e e e n n n n ++++>+++++⇔>++⎛⎫⎛⎫⎛⎫⎛⎫→∞+→+→+<<+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭最后不等式显然成立当时故9.求极限22222222221111lim 1111234111111112341324351111().2233442210.()lim (00, ()lim n n n n n n n n n n n n nxf x a nx ax nxf x nx a →∞→∞→∞⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭++==→→∞=≠+===+作函数)的图形.解解0;1/,0.x x ⎧⎨≠⎩1111.?,()[,]|()|,[,].,(),[,],max{||,||}1,|()|,[,].,|()|,[,],(),[,].12.f x a b M f x M x a b M N f x N x a b M M N f x M x a b M f x M x a b M f x M x a b <∀∈≤≤∀∈=+<∀∈<∀∈-<<∀∈1在关于有界函数的定义下证明函数在区间上为有界函数的充要条件为存在一个正的常数使得设存在常数使得M 取则有反之若存在一个正的常数使得则证12121212:()()[,],()()()()[,].,,|()|,|()|,[,].|()()||()||()|,|()()||()||()|,[,].113.:()cos 0y f x y g x a b f x g x f x g x a b M M f x M g x M x a b f x g x f x g x M M f x g x f x g x M M x a b f x x x xπ==+<<∀∈+≤+<+=<∀∈==证明若函数及在上均为有界函数则及也都是上的有界函数存在证明在的任一证,0().11(,),00,,,(),1()(,)0,()(21/2)cos(21/2)0,21/20().n x f x M n n M f n M n nf x f x n n n x f x δδδδδδπ→->><>=>-=→=++=→∞+→n 邻域内都是无界的但当时不是无穷大量任取一个邻域和取正整数满足和则故在无界.但是x 故当时不是无穷大量证11111000114.lim (1)ln (0).1ln 1,ln ln(1),.lim lim 10.ln(1)ln(1)lim lim ln(1)ln lim(1)ln 1,ln (1)ln ().ln(1)15.()()nn nn n n n n y y y y y n nn n x x x xx y x y n y x n y y y y e y y xn x x n y f x g x →∞→∞→∞→→→-=>-==+==-=++=+=+==-=→→∞+证明令则注意到我们有设及在实轴上有证00002022222220000.:()(),,()lim ()lim ()().1cos 116.lim.22sin 1cos 2sin 1sin 12lim lim lim lim 1422n n n n n x x x y y f x g x x x x f x f x g x g x x x x x y y x x y y →∞→∞→→→→→→===-=⎛⎫-==== ⎪⎝⎭定义且连续证明若与在有理数集合处处相等,则它们在整个实轴上处处相等.任取一个无理数取有理数序列证明证证0011000000001.2ln(1)17.:(1)lim 1;(2)lim .ln(1)(1)lim lim ln(1)ln lim(1)ln 1.(1)11(2)lim lim lim lim ln(1)ln(1)lim1.1x a xa y x y y y y y x a a a x x aa ax x x y y a a y e e e y x y y y e ye e e e e y e e e y x x x y ye e +→→→→→+→→→→→=+-==+=+=+==---====++==证明证0111018.()lim ()0,()lim ()()0.|()|,0||.0,0,0|||()|/.min{,},0||,|()()||()||()|,li x ax ay f x a f x y g x a f x g x g x M x a x a f x M x a f x g x f x g x M Mδεδδεδδδδεε→→====<<-<>><-<<=<-<=<=设在点附近有定义且有极限又设在点附近有定义,且是有界函数.证明设对于任意存在使得当时令则时故证m ()()0.x af xg x →=19.()(,),,()()|()|() () ()(),()(,).y f x c g x f x f x c g x c f x cc f x c g x g x =-∞+∞≤⎧⎪=>⎨⎪-<-⎩-∞+∞设在中连续又设为正的常数定义如下 当当当试画出的略图并证明在上连续0000000000000|()|,0,||lim ()lim ()()().(),0,||()lim ()lim ().(),().0,,0,x x x x x x x x f x c x x g x f x f x g x f x c x x f x c g x c c g x f x c g x c c δδδδεεδ→→→→<>-<===>>-<>=====><>一若则存在当时|f(x)|<c,g(x)=f(x),若则存在当时,g(x)=c,若则对于任意不妨设存在使证()0000121212|||()|.||.(),()(),|()()||()|,(),(),|()-()|0.()()min{(),}max{(),}().max{(),()}(|()()|()())/2.min x x f x c x x f x c g x f x g x g x f x c f x c g x c g x g x g x f x c f x c f x f x f x f x f x f x f x δεδεε-<-<-<≤=-=-<>==<=+--=-++得当时设若则若 则二利用证121212123123123111123{(),()}(|()()|(()())/2.120.()[,],[()()()],3,,[,].[,],().()()(),(),.()min{(),(),()},f x f x f x f x f x f x f x a b f x f x f x x x x a b c a b f c f x f x f x f x c x f x f x f x f x f ηηη=--++=++∈∈======设在上连续又设其中证明存在一点使得若则取即可否则设证31231313000000()min{(),(),()},()(),[,],,[,],().21.()(),()g(),,.0()g()()g()x f x f x f x f x f x f x x c a b f c y f x x g x x x kf x l x x k l l kf x l x x kf x l x x ηη=<<∈==+=+≠+在连续根据连续函数的中间值定理存在一点使得设 在点连续而在点附近有定义但在不连续问是否在连续其中为常数如果在连续;如果在解,l 0,000000||()[[()lg()]()]/.22.Dirichlet ..,()1;,()0;lim (),()11(1)lim 0;(2)lim (arctan )sin 12n n n n x x x x x g x kf x x kf x l x x x x D x x x D x D x D x x x x x →→∞→+∞=+-''→→→→+⎛⎫= ⎪+⎝⎭不连续,因否则将在连续证明函数处处不连续任意取取有理数列则取无理数列则故不存在在不连续.23.求下列极限:证222001/112132100;2tan 5tan 5/5(3)lim lim 5.ln(1)sin [[ln(1)]/]sin /1lim(1).24.()[0,),0().0,(),(),,().{x x y x y n n x x x x x x x x x x x y e y f x f x x a a f a a f a a f a π→→→→+=====++++=+==+∞≤≤≥===设函数在内连续且满足设是一任意数并假定一般地试证明11},lim .lim ,(),().(),{}()0(1,2,),{}n n n n n n n n n n n n a a l a l f x x f l l a f a a a a f a n a →∞→∞++====≤=≥=单调递减且极限存在若则是方程的根即单调递减.又单调递减有下界,证111lim ,lim lim ()(lim )().25.()(,),:(0)1,(1),()()().()((,)).()()().()()n n n n n n n n n x n n a l a l a f a f a f l y E x E E e E x y E x E y E x e x E x x E x E x E nx E x +→∞→∞→∞→∞======-∞+∞==+==∀∈-∞+∞++==故有极限.设则设函数在内有定义且处处连续并且满足下列条件证明用数学归纳法易得于是证11.,()(11)(1).1(0)(())()()(),().().1111,(1)()()()(),().11()()().,n n n n n n nn mmm n n n E n E E e E E n n E n E n e E n E n e E n e n E E n E n E e E E e n n n n m E E m E e e r E n n n -=++====+-=-=--======⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭设是正整数则于对于任意整数对于任意整数即对于所有有理数lim ().,,(),()lim ()lim ().nnn r x x x x n n n r e x x E x E x E x e ee e →∞→∞→∞=→====n 对于无理数取有理数列x 由的连续性的连续性习题2.1201.,.,.()2(0)(1),;(2),?(3)lim ,?x l O x x m x x x l x x m mx mx ∆→=≤≤∆∆∆∆∆∆设一物质细杆的长为其质量在横截面的分布上可以看作均匀的现取杆的左端点为坐标原点杆所在直线为轴设从左端点到细杆上任一点之间那一段的质量为给自变量一个增量求的相应增量求比值问它的物理意义是什么求极限问它的物理意义是什么2222222000(1)2()22(2)22(2).2(2)(2)2(2).(3)lim lim 2(2)4.lim x x x m x x x x x x x x x x x m x x x m x x x x x x x x m mx x x x x x∆→∆→∆→∆=+∆-=+∆+∆-=∆+∆∆∆+∆∆==+∆+∆∆∆∆∆∆=+∆=∆∆是到那段细杆的平均线密度.是细杆在点的线密度.解33332233222 00002.,:(1);(2)0;(3)sin5.()(1)lim(33)lim lim(33)3. (2)lim limlimxx xx xxy ax y p y xa x x axyxx x x x x x xa a x x x x axxyx∆→∆→∆→∆→→→==>=+∆-'=∆+∆+∆+∆-==+∆+∆=∆'==∆=根据定义求下列函数的导函数解00000limlim5(2)52cos sinsin5()sin522(3)lim lim55(2)552cos sin sin5(2)2222lim5lim cos lim5522xxx xx x xx x xx x xyx xx x x xx xx→→∆→∆→∆→∆→∆→===+∆∆+∆-'==∆∆+∆∆∆+∆==∆∆5cos5.2xx=00223.()(,()):(1)2,(0,1); (2)2,(3,11).(1)2ln2,(0)ln2,1ln2(-0),(ln2) 1.(2)2,(3)6,:116(3).4.2(0)(,)(0,0)xxy f x M x f xy M y x By y y x y xy x y y xy px p M x y x y===+''==-==+ ''==-=-=>>>求下列曲线在指定点处的切线方程切线方程切线方程试求抛物线上任一点处的切线斜率解,0,.2pF x⎛⎫⎪⎝⎭,并证明:从抛物线的焦点发射光线时其反射线一定平行于轴2000,().(),.,2,.2,.p py y M PMN Y y X x yy p y x N X y X x X x x y p p FN x FM p x FN FNM FMN M PQ x PMQ FNM FMN '===-=--=-=-=-=+=====+=∠=∠∠=∠=∠过点的切线方程：切线与轴交点(,0),故过作平行于轴则证2005.2341,.224,1,6,4112564(1),4 2.:6(1),.444y x x y x y x x y k y x y x y x y x =++=-'=+====⎛⎫-=-=+-=--=-+ ⎪⎝⎭曲线上哪一点的切线与直线平行并求曲线在该点的切线和法线方程切线方程:法线方程解323226.,,;(),,, (1)():(2)();(3)().()lim ()lim,lim ()limr R r R r R r R r g r GMrr R R g r R M G GM r R rg r r g r g r r GMr GMr R g r g r R RGM g r r →-→-→+→+⎧<⎪⎪=⎨⎪≥⎪⎩≠====离地球中心处的重力加速度是的函数其表达式为其中是地球的半径是地球的质量是引力常数.问是否为的连续函数作的草图是否是的可导函数明显地时连续.解,2lim (),()r R GMg r g r r R R→-==在连续.(2)33(3)()2(),()(),().r R g r GM GMg R g R g R g r r R R R-+-≠'''==-≠=时可导.在不可导227.(),:(1,3)(),(0)3,(2) 1.3(),()2.34111113,,3(),()3.2222P x y P x P P a b c P x ax bx c P x ax b b a b b a c a b P x x x ''===++=⎧⎪'=++=+=⎨⎪+=⎩==-=-+==-++求二次函数已知点在曲线上且解3222222222228.:(1)87,24 1.(2)(53)(62),5(62)12(53)903610.(3)(1)(1)tan (1)tan ,(2)tan (1)sec .9(92)(56)5(9)51254(4),56(56)y x x y x y x x y x x x x x y x x x x x y x x x x x x x x x x x x y y x x '=++=+'=+-=-++=+-'=+-=-=+-+++-+++'===++求下列函数的导函数22.(56)122(5)1(1),.11(1)x x y x y x x x ++'==-+≠=---23322222226(6)(1),.1(1)1(21)(1)1(7),.(8)10,1010ln1010(1ln10).sin cos sin (9)cos ,cos sin .(10)sin ,sin cos (s x x x x xx x x x x x x x x y x y x x x x x e e x x x x y y e e ey x y x x x x x xy x x y x x x x x y e x y e x e x e -'=≠=--+++-++-+-'==='==+=+-'=+=-+'==+=in cos ).x x +00000001001100009.:()()()(),()0().()()(1)(2).()()(),()0()()()()()()(()()())()(),(m k k k k k P x P x x x g x g x x P x m x P x k x P x k k P x x x g x g x P x k x x g x x x g x x x kg x x x g x x x h x h x ---=-≠'->=-≠''=-+-'=-+-=-定义若多项式可表为则称是的重根今若已知是的重根,证明是的重根证00)()0,()(1)kg x x P x k '=≠-由定义是的重根.000000010.()(,),()(),().()(0),(0)0.()(0)()(0)()(0)(0)lim lim lim (0),(0)0.()()11.(),lim 22x x x x f x a a f x f x f x f x f f f x f f x f f x f f f f x x xf x x f x x f x x f x→→→∆→--=''=-----'''==-=-=-+∆--∆'=∆若在中有定义且满足则称为偶函数设是偶函数,且存在试证明设在处可导证明证=000000000000000000000().()()()()()()1lim lim 22()()()()1lim 2()()()()11lim lim [()22x x x x x x f x x f x x f x x f x f x x f x x x x f x x f x f x x f x x x f x x f x f x x f x f x x x ∆→∆→∆→∆→∆→+∆--∆+∆--∆-⎡⎤=-⎢⎥∆∆∆⎣⎦+∆--∆-⎡⎤=+⎢⎥∆-∆⎣⎦+∆--∆-⎡⎤'=+=+⎢⎥∆-∆⎣⎦证002()]().12.,(0/2)()((),()):.f x f x y x t t P t x t y t OP x t t π''==<<=一质点沿曲线运动且已知时刻时质点所在位置满足直线与轴的夹角恰为求时刻时质点的位置速度及加速度.222222422222()()()tan ,()tan ,()()(tan ,tan ),()(sec ,2tan sec ),()(2sec tan ,2sec 4tan sec )2sec (sec ,2tan ).y t x t x t t y t t x t x t t t v t t t t v t t t t t t t t t ===='=''=+=位置解1/1/1/1/1/000013.,0()10, 00.1111(0)lim lim 1,(0)lim lim 0.1114.()||(),()()0.().()limxx x x x x x x x x xx f x ex x x x e e f f x e xe f x x a x x x a a f x x a f a ϕϕϕ→-→-→+→+-→⎧≠⎪=+⎨⎪=⎩=++''======++=-=≠='=求函数在的左右导数设其中在处连续且证明在不可导-+解证()()()()(),()lim ()().a x a a x x x a x a a a f a x a x aϕϕϕϕ-→---''=-==≠--+-f习题2.2()()()22221.,:111(2)[ln(1)],.[ln(1)](1).111(3)2.22x x xx x xx xx x x x''=-=-='''-=-=-=---'''⎡==⎣'''⎡=+=⎣=下列各题的计算是否正确指出错误并加以改正错错错3322222()221(4)ln|2sin|(14sin)cos,.2sin1ln|2sin|(14sin cos).2sin2.(())()|.() 1.(1)(),(0),(),(sin);(2)(),(sin);(3)u g xx x x xx xx x x xx xf g x f u f x xf x f f x f xd df x f xdx dx=='⎡⎤+=+⎣⎦+'⎡⎤+=+⎣⎦+''==+''''错记现设求求[]()[][]2222223(())(())?.(1)()2,(0)0,()2,(sin)2sin.(2)()()224.(sin)(sin)(sin)2sin cos sin2.(3)(())(()),(())(())().f g x f g xf x x f f x x f x xdf x f x x x x xdxdf x f x x x x xdxf g x f g x f g x f g x g x''''''====''===''==='''''=与是否相同指出两者的关系与不同解()()()222233312232323.2236(1),.111(2)sec,(cos)(cos)(cos)(cos)(sin)tan sec.(3)sin3cos5,3cos35sin5.(4)sin cos3,3sin cos cos33sin sin33sinx xy yx x xy x y x x x x x x x y x x y x xy x x y x x x x x---'==-=----'''===-=--='=+=-'==-=求下列函数的导函数:2(cos cos3sin sin3)3sin cos4.x x x x x x x-=22222222222232222222241sin 2sin cos cos (1sin )(sin )2(5),cos cos sin 2cos 2(1sin )(sin ).cos 1(6)tan tan ,tan sec sec 13tan sec tan tan (sec 1)tan .(7)sin ,s ax ax x x x x x x x y y x x x x x x x xy x x x y x x x x x x x x x y e bx y ae +-+-'==++='=-+=-+=-=-='==5422in cos (sin cos ).(8)cos 5cos sin 11(9)ln tan ,sec 24224tan 2411112tan cos 2sin 24242ax ax bx be bx e a bx b bx y y x x y y x x x x ππππππ+=+'==-=⎛⎫⎛⎫'=+=+ ⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭==⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭222cos 42411sec .cos sin()211()()1(10)ln (0,),.22()x x x x x a x a x a x a y a x a y a x a a x a x a x a ππ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭===+-++--'=>≠±==+-+-22222222224.:1(1)arcsin (0),11111(2)arctan (0),.1(3)arccos (||1),2arccos 1111(4)arctan ,.111(5)ar 2xy a y aa a x y a y a a a a a x x a y x x x y x x y y x x x xa y '=>==-'=>==+⎛⎫+ ⎪⎝⎭'=<=-'===-++=求下列函数的导函数csin (0),x a a>22222222(6)ln(0)212(7)arcsin,1ya xy aayxy xx'=+==+=>⎛⎫'=++===≠±+22222222221.112sgn(1)2.111(8)(0).212211sec2()tan()cos()s22x xyx xxxy a bxyxx xa b a b a b a b--'===++-⎫=>≥⎪⎪⎭⎛⎫'= ⎪⎝⎭==++-++-2in21.cos(9)(1ln(1ln(1ln(1 /.(10)(11)(12)xa b xy yy yy yy yy y=+=+++=++++ '=+⎡⎤'='=='==y y'==(13)ln(121(14)(ln(1)ln(31)ln(2),331211131321211.13132(15),(1).(16)xxxx e x e x x e y x y y x y x x x y y x x x y y x x x y e e y e e e e e ⎛⎫'==+==-=-+++-'-=++-+--⎡⎤'=++⎢⎥-+-⎣⎦'=+=+=+11112(0).ln ()ln ln ln ln .aaxa a xaaxa x a a a x a a x a ax a a x y x a a a y a x a a ax a aa aa x a aa x a a a ----=++>'=++=++222225.()1()()84,tan (),24001001()arctan ,()100110t x t t x t t t t t t t t θθθθ===='==+2一雷达的探测器瞄准着一枚安装在发射台上的火箭,它与发射台之间的距离是400m.设t=0时向上垂直地发射火箭,初速度为0,火箭以的匀加速度8m/s 垂直地向上运动;若雷达探测器始终瞄准着火箭.问:自火箭发射后10秒钟时,探测器的仰角的变化速率是多少?解222110,(10)0.1(/).505010101006.,2m t s θπθ'==⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭弧度在图示的装置中飞轮的半径为且以每秒旋转4圈的匀角速度按顺时针方向旋转.问:当飞轮的旋转角为=时,活塞向右移动的速率是多少?20()2cos8()16sin811()8,,,()16.2161616m/s.x t t x t t t t t x ππππαπππ='=-'====-活塞向右移动的速率是解习题2.323222(1)(1).1.0,?(1)10100.1(2)2(3)(1cos)2sin ,222.:0,()().()().()()3.()()(0),()()(0).o o o x o o o x x y x x x y x xy x x x x x x x x x x x x xx x x x x x αααααβ=→=++===-=→=====→=→当时下列各函数是的几阶无穷小量阶.阶.阶.已知当时试证明设试证明证00(1)(1)(1)()()()(0).()()()().()()().4.(1)sin ,/4.sin cos ,1,1.444(2)(1)(0).o o o o o o o x x x x x x x x x x xx x x x y x x x y x x x y dy dx y x y ααβαβαβππππα+=→+=+=+=+=⎛⎫⎫⎫''===+=+=+ ⎪⎪⎪⎝⎭⎭⎭=+>':上述结果有时可以写成计算下列函数在指定点处的微分:是常数证122(1),(0),.5.1222(1)1,,.11(1)(1)(2),(1).(1).26.(1),3 3.001,11,(3).222.001x x x x x x y dy dx x dx y y dy x x x x y xe y e xe e x dy e x dx y x x x y y αααα-'=+==-'==-+=-=-++++'==+=+=+=≠-''=-∆=求下列各函数的微分:设计算当由变到时函数的增量和向相应的微分.22解 y =-(x -1)1222113333332220.0010.0011,.2.00127..1.162(1) 2.002.5328.:11(1)(0).0,.33(2)()()(,,).2()2()dy y x y a a xy y y x x a y b c a b c x a y b y ---=-=-==+=⎛⎫''+=>+==- ⎪⎝⎭-+-='-+-=求下列方程所确定的隐函数的导函数为常数0,.x ay y b-'=--。

对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关，1系电过，力管根保线据护敷生高设产中技工资术0艺料不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层，机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试22下卷，高总而中体且资配可料置保试时障卷，各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看2度并22工且22作尽22下可22都能2可地护1以缩关正小于常故管工障路作高高；中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整，处核或理对者高定对中值某资，些料审异试核常卷与高弯校中扁对资度图料固纸试定，卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置，跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等，料，编5试要写、卷求重电保技要气护术设设装交备备4置底高调、动。中试电作管资高气，线料中课并3敷试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术，技含以来术线及避槽系免、统不管启必架动要等方高多案中项；资方对料式整试，套卷为启突解动然决过停高程机中中。语高因文中此电资，气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技，进术合行，理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对：于于在调差分试动线过保盒程护处中装，高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时，术，作是应为指采调发用试电金人机属员一隔，变板需压进要器行在组隔事在开前发处掌生理握内；图部同纸故一资障线料时槽、，内设需，备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切，验除线报从缆告而敷与采设相用完关高毕技中，术资要资料进料试行，卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。