第17章 空气动力计算

车辆空气动力学与车身造型空气动力学（Aerodynamics）是研究物体在与周围空气作相对运动时两者之间相互作用力的关系及运动规律的科学，它属于流体力学的一个重要分支。

长期以来，空气动力学成果的应用多侧重于航空及气象领域，特别是在航空领域内这门科学取得了巨大的进展，给汽车或路面车辆的空气动力学（Automotive Aerodynamics-Road Vehicle Aerodynamics）研究提供了借鉴。

然而进一步的深入研究表明，汽车或车辆的空气动力学问题从理论到实际两方面都与航空等问题有本质的区别，汽车空气动力学已逐步发展成为了空气动力学的一个独立分支，在方程式赛车领域更是得到了极大的应用。

下面就谈谈赛车中空气动力学的应用。

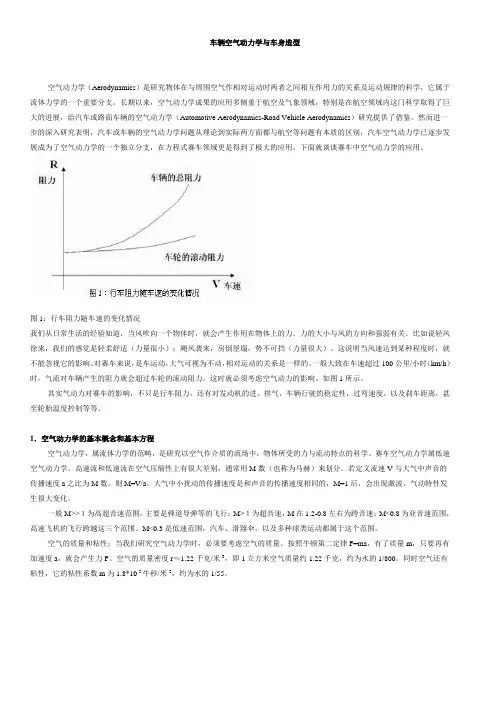
图1：行车阻力随车速的变化情况我们从日常生活的经验知道，当风吹向一个物体时，就会产生作用在物体上的力。

力的大小与风的方向和强弱有关。

比如说轻风徐来，我们的感觉是轻柔舒适（力量很小）；飓风袭来，房倒屋塌，势不可挡（力量很大）。

这说明当风速达到某种程度时，就不能忽视它的影响。

对赛车来说，是车运动，大气可视为不动，相对运动的关系是一样的。

一般大致在车速超过100公里/小时（km/h）时，气流对车辆产生的阻力就会超过车轮的滚动阻力。

这时就必须考虑空气动力的影响。

如图1所示。

其实气动力对赛车的影响，不只是行车阻力，还有对发动机的进、排气，车辆行驶的稳定性，过弯速度，以及刹车距离，甚至轮胎温度控制等等。

1．空气动力学的基本概念和基本方程空气动力学，属流体力学的范畴，是研究以空气作介质的流场中，物体所受的力与流动特点的科学。

赛车空气动力学属低速空气动力学。

高速流和低速流在空气压缩性上有很大差别，通常用M数（也称为马赫）来划分。

若定义流速V与大气中声音的传播速度a之比为M数，则M=V/a。

大气中小扰动的传播速度是和声音的传播速度相同的，M=1后，会出现激波，气动特性发生很大变化。

一般M>>１为高超音速范围，主要是弹道导弹等的飞行；M>１为超音速，M在1.2-0.8左右为跨音速；M<0.8为亚音速范围，高速飞机的飞行跨越这三个范围。

跨声速非定常空气动力计算Computation on Transonic Unsteady Aerodynamics北京大学力学与工程科学系理论与应用力学专业 00级陈雪梅摘要颤振问题一直是高速飞行器设计中的一大难题，特别在跨声速区段。

本文利用FLUENT6.1对一模型机翼的颤振行为进行了数值模拟，仿真机翼在高速气流中受激后扭曲变形最后发展成颤振的全过程，并对这一计算结果进行了初步分析，所得的算法具有普遍意义。

关键词：颤振，空气动力学，动网格[引言]早期的飞行器设计中的空气动力学分析都是将机翼﹑机身和其他气动部件当作刚体来处理。

但自第一架飞机诞生以来，空气动力学与飞机结构弹性的相互作用问题已经对航空技术的发展产生了重大影响，特别在‘彗星号’失事以后，人们对此倍加关心。

飞机在空气载荷作用下会出现可观的变形，这种变形将改变空气动载荷的分布，而它反过来又使变形发生变化。

在这种相互作用过程中，会引起振动，学术界称之为颤振。

这是一种自激振荡，它不断从气流中吸收能量。

当飞机发生颤振时，轻则出现不稳定和振动现象，重则因它引起材料‘疲劳’从而导致飞机在空中解体，以至机毁人亡。

在莱特兄弟首次试飞前，兰利的“空中旅行者”作了两次不成功的飞行试验。

第二次试飞时机翼和尾翼毁坏了，失败原因众说纷纭，气动弹性可能是第二次失败的罪魁祸首。

第一次世界大战中，英国的DH-9飞机尾翼颤振导致了飞行员死亡。

对此，英国空气动力学家贝尔斯托（L. Bairstow）首先对颤振进行了理论研究。

随着飞机速度的提高，空气动力增大，而重量小的结构形式使机翼抵抗变形的能力下降，所以气动弹性问题便得严重起来。

20世纪30年代初英国一家飞机连续发生有气动弹性引起的颤振事故，促使航空工程界对气动弹性问题普遍重视起来[摘自参考文献3，P118]。

其间的理论研究颇有成效。

美国力学家西奥多森（T. Theodorson）提交的研究报告对美国航空工业界建立颤振分析方法起了巨大作用。

空气动力学公式
以下是一些常见的空气动力学公式：
1.压力公式：P=1/2ρv²，其中P表示压力，ρ表示空气密度，v表
示速度。

2.升力公式：L=Cl×1/2ρv²×S，其中L表示升力，Cl表示升力系数，S表示受力面积。

3.阻力公式：D=Cd×1/2ρv²×S，其中D表示阻力，Cd表示阻力系数，S表示受力面积。

4.马赫数公式：M=v/a，其中M表示马赫数，v表示速度，a表示音速。

5. 空气动力学力公式：F = ma = (P2-P1) × A，其中F表示力，m
表示质量，a表示加速度，P表示压力，A表示受力面积。

6.爱丁顿近似公式：Cd=2∑((Fi/v²)×Δii),其中Cd表示阻力系数，F表示阻力，v表示速度，Δr表示重心位置的移动量。

7. 激波角公式：θ = arcsin(1/M)，其中θ表示激波角，M表示马
赫数。

8.汉克斯公式：L/D=Cl/Cd，其中L/D表示升阻比，Cl表示升力系数，Cd表示阻力系数。

9. 斯托克斯公式: Fd= 6πμrv，其中Fd表示粘滞阻力，μ表示空
气粘度，r表示颗粒半径，v表示速度。

以上仅是空气动力学公式中的部分，具体使用还要根据具体问题进行。

第17章 流体动力学分析 计算流体动力学分析（机进行数值计算，模拟流体流动时的各种相关物理现象，包括流动、热传导、声场等。

计算流体动力学分析广泛应用于航空航天器设计、★ 掌握流体动力学分析的基础理论。

17.1 流体动力学基础对于所有流动，都需要求解质量和动量守恒方程。

对于包含传热或可压性流动，还需要增加能量守恒方程。

如果是湍流问题，还要选择求解相应的湍流模型。

17.1.1 质量守恒方程适合可压和不可压流动的质量守恒形式为：m i iS u x t =∂∂+∂∂)(ρρ 式中：ρ为密度，t 为时间，i u 为速度张量，i x 为坐标张量。

等式左边第1项是密度变化率，当求解不可压缩流动时该项为零；第2项是质量流密度的散度；右边的源项m S 是稀疏相增加到连续相中的质量，如液体蒸发变成气体或者质量源项，在单相流中，该源项为零。

17.1.2 动量守恒方程在惯性坐标系下，i 方向的动量守恒方程为：第17章 流体动力学分析i i jij i j i j i F g x x p u u x u t ++∂∂+∂∂−=∂∂+∂∂ρτρρ)()( 式中：ρ为密度；t 为时间；i u 、j u 为速度张量；i x 、j x 为坐标张量；i g ρ为重力体积力；p 是静压；i F 是重力体积力和其他体积力（如源于两相之间的作用），i F 还可以包括其他模型源项或者自定义的源项；ij τ是应力张量，定义为：ijl l i j j i ij x u x u x u δμμτ∂∂−⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛∂∂+∂∂=32 式中：μ为流体粘性系数。

通过求解能量方程，可以计算流体和固体区域之间的传热问题。

能量守恒方程形式如下： h eff ij j j j j i eff i i i S u J h x T k x p E u x E t ++−∂∂∂∂=+∂∂+∂∂∑′′′)(())(()(τρρ 式中：T 为温度；k k k t eff +=，为有效导热系数（湍流导热系数根据湍流模型来定义）；j J ′是组分j ′的扩散通量。

跨声速非定常空气动力计算Computation on Transonic Unsteady Aerodynamics北京大学力学与工程科学系理论与应用力学专业 00级陈雪梅摘要颤振问题一直是高速飞行器设计中的一大难题，特别在跨声速区段。

本文利用FLUENT6.1对一模型机翼的颤振行为进行了数值模拟，仿真机翼在高速气流中受激后扭曲变形最后发展成颤振的全过程，并对这一计算结果进行了初步分析，所得的算法具有普遍意义。

关键词：颤振，空气动力学，动网格[引言]早期的飞行器设计中的空气动力学分析都是将机翼﹑机身和其他气动部件当作刚体来处理。

但自第一架飞机诞生以来，空气动力学与飞机结构弹性的相互作用问题已经对航空技术的发展产生了重大影响，特别在‘彗星号’失事以后，人们对此倍加关心。

飞机在空气载荷作用下会出现可观的变形，这种变形将改变空气动载荷的分布，而它反过来又使变形发生变化。

在这种相互作用过程中，会引起振动，学术界称之为颤振。

这是一种自激振荡，它不断从气流中吸收能量。

当飞机发生颤振时，轻则出现不稳定和振动现象，重则因它引起材料‘疲劳’从而导致飞机在空中解体，以至机毁人亡。

在莱特兄弟首次试飞前，兰利的“空中旅行者”作了两次不成功的飞行试验。

第二次试飞时机翼和尾翼毁坏了，失败原因众说纷纭，气动弹性可能是第二次失败的罪魁祸首。

第一次世界大战中，英国的DH-9飞机尾翼颤振导致了飞行员死亡。

对此，英国空气动力学家贝尔斯托（L. Bairstow）首先对颤振进行了理论研究。

随着飞机速度的提高，空气动力增大，而重量小的结构形式使机翼抵抗变形的能力下降，所以气动弹性问题便得严重起来。

20世纪30年代初英国一家飞机连续发生有气动弹性引起的颤振事故，促使航空工程界对气动弹性问题普遍重视起来[摘自参考文献3，P118]。

其间的理论研究颇有成效。

美国力学家西奥多森（T. Theodorson）提交的研究报告对美国航空工业界建立颤振分析方法起了巨大作用。

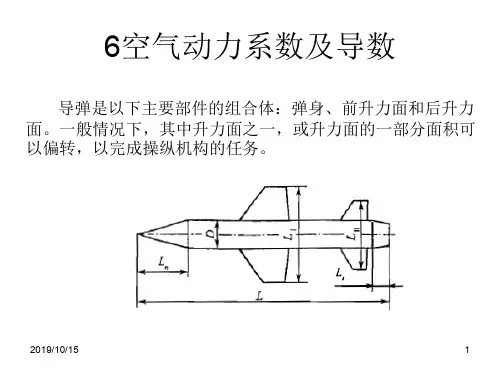
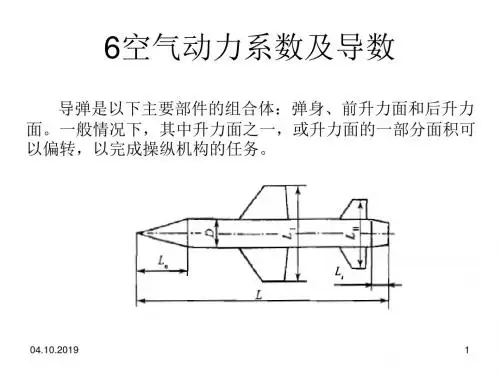
第一章 飞行器基本知识1.1飞行器几何参数飞行器通常由机翼、机身、尾翼以及动力装置等部件组成。

对于气动正问题及气动分析而言，已知飞行器几何外形，求其气动参数。

要解决这一问题首先要计算出飞行器各部件及组合体的几何参数。

当机翼和机身组合成一体时，机翼中间一部分面积为机身所遮蔽。

它外露在气流中的部分两边合起来，所构成的机翼为外露翼，由下标“wl ”表示 在组合体中把外露翼根部的前后缘向机身内延长并交于机身纵对称面，这样的机翼成为毛机翼。

第二章 机翼的气动特性分析2.1机翼几何参数2.1.1 翼型的几何参数翼型的前缘点与后缘点的连线称为弦线。

他们之间的距离称为弦长，用符号b 表示，是翼型的特征长度。

可以想象翼型是由厚度分布)(x y c 和中弧线分布)(x y f 叠加而成的，对于中等厚度和弯度的翼型，上下翼面方程可以写成 )()()(,x y x y x y c f L U += （2—1） 式中的正号用于翼型上表面，负号用于下表面。

b x x /=，b y y /=分别为纵、横向无量纲坐标。

相对厚度和相对弯度b c c /=，b f f /=。

最大厚度位置和最大弯度位置分别用c x 和f x 或用无量纲量b x c /和b x f /表示。

翼型前缘的内切圆半径叫做前缘半径，用L r 表示，后缘角τ是翼型上表面和下表面在后缘处的夹角。

2.1.2 机翼的几何参数1.机翼平面形状：根梢比、展弦比和后掠角机翼面积S 是指机翼在xOz 平面上的投影面积，即22()l l S b z dz-=ò（2—2）式中，b （z ）为当地弦长。

几何平均弦长pj b 和平均气动弦长A b 分别定义为/pj b S l = （2—3）2202()l A b b z dz S =ò （2—4）显然，pj b 是面积和展长都与原机翼相等的当量矩形翼的弦长；而A b 是半翼面心所在的展向位置的弦长，通常取A b 作为纵向力矩的参考长度。

空气动力学是力学的一个分支，它主要研究物体在同气体作相对运动情况下的受力特性、气体流动规律和伴随发生的物理化学变化。

空气动力学重点研究飞行器的飞行原理，是航空航天技术最重要的理论基础之一。

气体流动在不同的速度范围呈现不同的特点。

空气动力学的发展经历了低速、高速和新变革三个时期。

它是在流体力学的基础上，随着航空工业和喷气推进技术的发展而成长起来的一个学科。

空气动力学 - 简介相关书籍空气动力学是研究空气和其他气体的运动以及它们与物体相对运动时相互作用的科学，简称为气动力学。

空气动力学重点研究飞行器的飞行原理，是航空航天技术最重要的理论基础之一。

在任何一种飞行器的设计中，必须解决两方面的气动问题：一是在确定新飞行器所要求的性能后，寻找满足要求的外形和气动措施；一是在确定飞行器外形和其他条件后，预测飞行器的气动特性，为飞行器性能计算和结构、控制系统的设计提供依据。

这些在飞行速度接近到超过声速（又称音速）时更为重要。

20世纪以来，飞机和航天器的外形不断改进，性能不断提高，都是与空气动力学的发展分不开的。

亚音速飞机为获得高升阻比采用大展弦比机翼；跨音速飞机为了减小波阻采用后掠机翼，机翼和机身的布置满足面积律；超音速飞机为了利用旋涡升力采用细长机翼（见机翼空气动力特性）；高超音速再入飞行器为了减少气动加热采用钝的前缘形状，这些都是在航空航天技术中成功地应用空气动力学研究成果的典型例子。

除此以外，空气动力学在气象、交通、建筑、能源、化工、环境保护、自动控制等领域都得到广泛的应用。

空气动力学 - 学科分支空气动力学空气动力学是流体力学的一个分支。

气体流动在气体流动在不同的速度范围呈现不同的特点。

飞行器的飞行马赫数大于0.3时，就必须考虑空气压缩性。

当飞行速度接近音速时，在飞行器的绕流中会出现局部的超音速区，在其后形成激波，使迎面阻力剧增。

当飞行速度超过音速几倍时，由于高速气流的温度升高，气体内部发生种种物理化学变化，这时必须同时考虑气体的热力现象和动力现象，研究这些现象的学科就是空气动力学的一个分支气动热力学。

理论空气量计算范文理论空气量计算是空气动力学中的一个重要问题，用于确定空气对物体的作用力大小。

在大气中的物体受到的空气阻力与流过物体的空气量有关，因此了解理论空气量的计算方法对于物体的风洞试验设计和风力发电等领域都具有重要的意义。

第一种方法是通过测量空气速度来计算理论空气量。

在风洞实验或空气动力学研究中，可以通过安装在管道或试验物体上的风速仪等设备来测量流过的空气速度。

根据流体力学中的公式Q=A×v，其中Q为流量，A为流经截面的面积，v为流速，可以利用测得的空气速度及截面面积来计算理论空气量。

第二种方法是通过测量空气密度来计算理论空气量。

空气密度是指单位体积内的空气质量，一般用ρ表示。

理论空气量可以通过测量空气的密度来计算。

常见的空气密度测量方法有测量试验室温度和压力以及气体混合比例等方法。

由于温度和压力都会对气体密度产生影响，所以在计算理论空气量时需要考虑这些因素。

在实际计算中，可以根据已知的密度和速度通过公式Q=ρ×v×A来计算理论空气量。

其中Q为理论空气量，ρ为空气密度，v为流速，A为流经截面的面积。

例如，假设需要计算风力发电机叶片所受到的空气阻力，已知风力发电机叶片所在位置的空气速度为10 m/s，空气密度为1.2 kg/m³，叶片流经截面的面积为5 m²，可以通过公式Q=ρ×v×A计算出阻力的大小。

Q=1.2×10×5=60 kg/s因此，风力发电机叶片所受到的理论空气量为60 kg/s。

总结起来，理论空气量计算方法主要有通过测量空气速度和密度来实现。

通过测量空气速度和通过测量空气密度，可以利用公式Q=ρ×v×A 来计算理论空气量。

这种计算方法在空气动力学研究和风洞试验中具有重要的意义。