创新设计2016_2017学年高考数学第二章点直线平面之间的位置关系2.3.3直线与平面垂直的性质课时作业
- 格式:doc
- 大小:392.00 KB
- 文档页数:5


山西省忻州市2016-2017学年高中数学第二章点、直线、平面之间的位置关系2.2 直线与平面、平面与平面平行测试题(无答案)新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山西省忻州市2016-2017学年高中数学第二章点、直线、平面之间的位置关系2.2 直线与平面、平面与平面平行测试题(无答案)新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山西省忻州市2016-2017学年高中数学第二章点、直线、平面之间的位置关系2.2 直线与平面、平面与平面平行测试题(无答案)新人教A版必修2的全部内容。
直线与平面、平面与平面平行本试卷满分70+5分一.选择题(每小题5分,共25分)1.若平面α和平面相交于直线L,直线a在平面α内但不与直线L重合,则直线a与平面的位置关系是 ( )A。
相交 B.平行C.相交或平行D. a在平面内2.在正方体ABCD—A1B1C1D1中,下列四对截面中彼此平行的一对截面是()A.面A1BC1和面ACD1 B。
面BDC1和面B1D1CC。
面B1D1D和面BDA D。
面A1DC1和面AD1C3.已知甲命题是“如果直线a∥b,那么a∥平面α”,乙命题是“如果a∥平面α,那么a∥b"。
使上面两个命题都成立,需分别添加的条件是 ( )A.甲:“b⊂α”,乙:“b⊂α”B.甲:“b⊂α”,乙:“a⊂β且α∩β=b"C。
甲:“aα,b⊂α”,乙:“a⊂β且α∩β=b”D.甲:“aα,b⊂α”,乙:“b∥α”4。
直线a∥平面,平面内有n条直线相交于一点,那么这n条直线中与直线a平行的( )A。



第二章点、直线、平面之间的地址关系空间点、直线、平面之间的地址关系一、平面1、平面及其表示2、平面的基本性质①公义 1:A lB llAB②公义 2:不共线的三点确定一个平面③公义 3:Pl 则P lP二、点与面、直线地址关系1、A1、点与平面有 2 种地址关系2、B1、A l2、点与直线有 2 种地址关系2、 B l三、空间中直线与直线之间的地址关系1、异面直线2、直线与直线的地址关系订交共面平行异面3、公义 4 和定理公义 4:l1 Pl3l1 Pl 2l 2 Pl3定理:空间中若是两个角的两边分别对应平行,那么这两个角相等或互补。
4、求异面直线所成角的步骤:① 作:作平行线获取订交直线;② 证:证明作出的角即为所求的异面直线所成的角;③ 构造三角形求出该角。
提示: 1、作平行线常有方法有:直接平移,中位线,平行四边形。
2、异面直线所的角的范围是00 ,900。
四、空间中直线与平面之间的地址关系地址关系直线 a在平面内直线 a与平面订交直线 a与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a a I Aa P图形表示五、空间中平面与平面之间的地址关系地址关系两个平面平行两个平面订交公共点没有公共点有一条公共直线符号表示P I a图形表示直线、平面平行的判断及其性质一、线面平行1、判断:ba b Pb Pa(线线平行,则线面平行)2、性质:a PaPa b b(线面平行,则线线平行)二、面面平行1、判断:aba b P Pa Pb P(线面平行,则面面平行)2、性质 1:PI a a PbI b(面面平行,则线面平行)性质 2:Pm Pm(面面平行,则线面平行)说明( 1)判断直线与平面平行的方法:① 利用定义:证明直线与平面无公共点。
② 利用判判定理:从直线与直线平行等到直线与平面平行。
③ 利用面面平行的性质:两个平面平行,则其中一个平面内的直线必平行于另一个平面。
(2)证明面面平行的常用方法①利用面面平行的定义:此法一般与反证法结合。
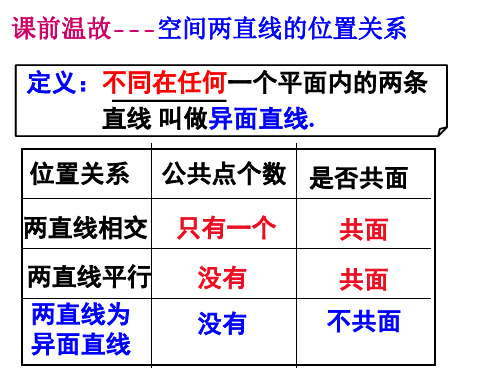
§1.2 点、线、面之间的位置关系1.2.1 平面的基本性质1.公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.用符号表示为:⎭⎪⎬⎪⎫A ∈αB ∈α⇒AB ⊂α 2.公理2:经过不在同一条直线上的三点,有且只有一个平面.简单说成,不共线的三点确定一个平面. (1)推论1 经过一条直线和这条直线外的一点,有且只有一个平面.(2)推论2 经过两条相交直线,有且只有一个平面.(3)推论3 经过两条平行直线,有且只有一个平面.3.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.用符号表示为:⎭⎪⎬⎪⎫P ∈αP ∈β⇒α∩β=l 且P ∈l .一、填空题1.下列命题:①书桌面是平面;②8个平面重叠起来,要比6个平面重叠起来厚;③有一个平面的长是50 m ,宽是20 m ;④平面是绝对的平、无厚度,可以无限延展的抽象数学概念.其中正确的是________.2.若点M 在直线b 上,b 在平面β内,则M 、b 、β之间的关系用符号可记作____________.3.已知平面α与平面β、γ都相交,则这三个平面可能的交线有________条.4.已知α、β为平面,A 、B 、M 、N 为点,a 为直线,下列推理错误的是__________(填序号).①A ∈a ,A ∈β,B ∈a ,B ∈β⇒a ⊂β; ②M ∈α,M ∈β,N ∈α,N ∈β⇒α∩β=MN ;③A ∈α,A ∈β⇒α∩β=A ; ④A 、B 、M ∈α,A 、B 、M ∈β,且A 、B 、M 不共线⇒α、β重合.5.空间中可以确定一个平面的条件是________.(填序号)①两条直线; ②一点和一直线; ③一个三角形; ④三个点.6.空间有四个点,如果其中任意三个点不共线,则经过其中三个点的平面有__________个.7.把下列符号叙述所对应的图形(如图)的序号填在题后横线上.(1)AD/∈α,a ⊂α________. (2)α∩β=a ,PD/∈α且PD/∈β________.(3)a ⊄α,a ∩α=A________. (4)α∩β=a ,α∩γ=c ,β∩γ=b ,a ∩b ∩c =O________.8.已知α∩β=m ,a ⊂α,b ⊂β,a ∩b =A ,则直线m 与A 的位置关系用集合符号表示为________.9.下列四个命题:①两个相交平面有不在同一直线上的三个公共点; ②经过空间任意三点有且只有一个平面;③过两平行直线有且只有一个平面; ④在空间两两相交的三条直线必共面.其中正确命题的序号是________.二、解答题10.如图,直角梯形ABDC中,AB∥CD,AB>CD,S是直角梯形ABDC所在平面外一点,画出平面SBD和平面SAC的交线,并说明理由.11.如图所示,四边形ABCD中,已知AB∥CD,AB,BC,DC,AD(或延长线)分别与平面α相交于E,F,G,H,求证:E,F,G,H必在同一直线上.证明几点共线的方法:先考虑两个平面的交线,再证有关的点都是这两个平面的公共点,或先由某两点作一直线,再证明其他点也在这条直线上.1.2.2空间两条直线的位置关系1.空间两条直线的位置关系有且只有三种:________、____________、____________.2.公理4:平行于同一条直线的两条直线____________.3.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角____ 或____.4.异面直线(1)定义:不同在任何一个平面内的两条直线叫做异面直线.(2)判定定理:过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线.5.异面直线所成的角:直线a,b是异面直线,经过空间任一点O,作直线a′,b′,使__________,__________,我们把a′与b′所成的锐角或直角叫做异面直线a与b所成的角.若两条直线所成的角是直角,则两条异面直线互相垂直,两条异面直线所成的角α的取值范围是____________.一、填空题1.若空间两条直线a,b没有公共点,则其位置关系是____________.2.若a和b是异面直线,b和c是异面直线,则a和c的位置关系是______________.3.在正方体ABCD—A1B1C1D1中,与对角线AC1异面的棱共有________条.4.空间四边形的两条对角线相互垂直,顺次连结四边中点的四边形的形状是________.5.给出下列四个命题:①垂直于同一直线的两条直线互相平行;②平行于同一直线的两直线平行;③若直线a,b,c满足a∥b,b⊥c,则a⊥c;④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线.其中假命题的个数是________.6.有下列命题:①两条直线和第三条直线成等角,则这两条直线平行;②四条边相等且四个角也相等的四边形是正方形;③经过直线外一点有无数条直线和已知直线垂直;④若∠AOB=∠A1O1B1,且OA∥O1A1,则OB∥O1B1.其中正确命题的序号为________.7.空间两个角α、β,且α与β的两边对应平行且α=60°,则β为________.8.已知正方体ABCD—A′B′C′D′中:(1)BC′与CD′所成的角为________;(2)AD与BC′所成的角为________.9.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论:①AB⊥EF;②AB与CM所成的角为60°;③EF与MN是异面直线;④MN∥CD.以上结论中正确结论的序号为________.二、解答题10.已知棱长为a的正方体ABCD-A1B1C1D1中,M,N分别是棱CD、AD的中点.求证:(1)四边形MNA1C1是梯形;(2)∠DNM=∠D1A1C1.11.如图所示,在空间四边形ABCD中,AB=CD且AB与CD所成的角为30°,E、F分别是BC、AD的中点,求EF与AB所成角的大小.作异面直线所成的角,可通过多种方法平移产生,主要有三种方法:①直接平移法(可利用图中已有的平行线);②中位线平移法;③补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).1.2.3 直线与平面的位置关系12.直线与平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.用符号表示为a⊄α,b⊂α且a∥b⇒a∥α.一、填空题1.以下说法(其中a,b表示直线,α表示平面)正确的个数为________.①若a∥b,b⊂α,则a∥α;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,b⊂α,则a∥b.2.已知a,b是两条相交直线,a∥α,则b与α的位置关系是________.3.如果平面α外有两点A、B,它们到平面α的距离都是a,则直线AB和平面α的位置关系是_____________.4.在空间四边形ABCD中,E、F分别是AB和BC上的点,若AE∶EB=CF∶FB=1∶3,则对角线AC和平面DEF的位置关系是________.5.过直线l外两点,作与l平行的平面,则这样的平面为____________个.6.过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有________条.7.经过直线外一点有________个平面与已知直线平行.8.如图,在长方体ABCD-A1B1C1D1的面中:(1)与直线AB平行的平面是______________;(2)与直线AA1平行的平面是______________;(3)与直线AD平行的平面是______________.9.在正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与过点A,E,C的平面的位置关系是___________.二、解答题10.如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱BC、C1D1的中点.求证:EF∥平面BDD1B1.11.如图所示,P是▱ABCD所在平面外一点,E、F分别在PA、BD上,且PE∶EA=BF∶FD.求证:EF∥平面PBC.直线与平面平行的判定方法(1)利用定义:证明直线a与平面α没有公共点.这一点直接证明是很困难的,往往借助于反证法来证明.(2)利用直线和平面平行的判定定理:a⊄α,a∥b,b⊂α,则a∥α.使用定理时,一定要说明“不在平面内的一条直线和平面内的一条直线平行”,若不注明和平面内的直线平行,证明过程就不完整.因此要证明a∥平面α,则必须在平面α内找一条直线b,使得a∥b,从而达到证明的目的.证明线线平行时常利用三角形中位线、平行线分线段成比例定理等.。
2.3.3 直线与平面垂直的性质
【课时目标】 1.理解直线和平面垂直的性质定理,并能用文字、符号和图形语言描述定理.2.能够灵活地应用线面垂直的性质定理证明相关问题.3.理解并掌握“平行”与“垂直”之间的相互转化.
文字语言 垂直于同一个平面的两条直线________ 符号语言 错误!⇒________
图形语言
作用
①线面垂直⇒线线平行
②作平行线
一、选择题
1.下列说法正确的是( )
A .若l 上有无数个点不在平面α内,则l ∥α
B .若直线l 与平面α垂直,则l 与α内的任一直线垂直
C .若E 、F 分别为△ABC 中AB 、BC 边上的中点,则EF 与经过AC 边的所有平面平行
D .两条垂直的直线中有一条和一个平面平行,则另一条和这个平面垂直
2.若M 、n 表示直线,α表示平面,则下列命题中,正确命题的个数为( )
①
⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α;②
⎭⎪⎬⎪
⎫m ⊥αn ⊥α⇒M ∥n ; ③
⎭
⎪⎬⎪
⎫m ⊥αn ∥α⇒M ⊥n; ④
⎭
⎪⎬⎪
⎫m ∥αm ⊥n ⇒n ⊥α. A .1B .2C .3D .4
3.已知直线PG ⊥平面α于G ,直线EF ⊂α,且PF ⊥EF 于F ,那么线段PE ,PF ,PG 的大小关系是( )
A .PE >PG >PF
B .PG >PF >PE
C .PE >PF >PG
D .PF >P
E >PG
4.PA 垂直于以AB 为直径的圆所在平面,C 为圆上异于A ,B 的任一点,则下列关系不正确的是( )
A .PA ⊥BC
B .B
C ⊥平面PAC C .AC ⊥PB
D .PC ⊥BC 5.下列命题:
①垂直于同一直线的两条直线平行; ②垂直于同一直线的两个平面平行; ③垂直于同一平面的两条直线平行;
④垂直于同一平面的两平面平行.
其中正确的个数是( )
A.1B.2C.3D.4
6.在△ABC所在的平面α外有一点P,且PA=PB=PC,则P在α内的射影是△ABC的( ) A.垂心B.内心C.外心D.重心
二、填空题
7.线段AB在平面α的同侧,A、B到α的距离分别为3和5,则AB的中点到α的距离为________.
8.直线a和b在正方体ABCD-A1B1C1D1的两个不同平面内,使a∥b成立的条件是________.(只填序号)
①a和b垂直于正方体的同一个面;②a和b在正方体两个相对的面内,且共面;③a和b平行于同一条棱;④a和b在正方体的两个面内,且与正方体的同一条棱垂直.9.如图所示,平面ABC⊥平面ABD,∠ACB=90°,CA=CB,△ABD是正三角形,O为AB 中点,则图中直角三角形的个数为________.
三、解答题
10.如图所示,在正方体ABCD—A1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.
求证:(1)MN∥AD1;
(2)M是AB的中点.
11.如图所示,设三角形ABC的三个顶点在平面α的同侧,AA′⊥α于A′,BB′⊥α于B′,CC′⊥α于C′,G、G′分别是△ABC和△A′B′C′的重心,求证:GG′⊥α.
能力提升
12.如图,△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,CE=CA=2BD,M是EA的中点,N是EC的中点,
求证:平面DMN∥平面ABC.
13.如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M,N分别是A1B,B1C1的中点.
(1)求证:MN⊥平面A1BC;
(2)求直线BC1和平面A1BC所成的角的大小.
1.直线和平面垂直的性质定理可以作为两条直线平行的判定定理,可以并入平行推导链中,实现平行与垂直的相互转化,即线线垂直⇒线面垂直⇒线线平行⇒线面平行.2.“垂直于同一平面的两条直线互相平行”、“垂直于同一直线的两个平面互相平行”都是真命题.但“垂直于同一直线的两条直线互相平行”、“垂直于同一平面的两个平面互相平行”都是假命题.
2.3.3 直线与平面垂直的性质答案
知识梳理
平行 a∥b 作业设计
1.B [由线面垂直的定义知B 正确.]
2.C [①②③正确,④中n 与面α可能有:n ⊂α或n ∥α或相交(包括n ⊥α).] 3.C [由于PG⊥平面α于G ,PF⊥EF, ∴PG 最短,PF<PE ,
∴有PG<PF<PE .故选C .]
4.C [PA⊥平面ABC ,得PA⊥BC,A 正确;
又BC⊥AC,∴BC⊥面PAC ,∴BC⊥PC,B 、D 均正确. ∴选C .]
5.B [由线线、线面垂直与平行的性质知②③正确,选B .]
6.C [设P 在平面α内的射影为O ,易证△PAO ≌△PBO ≌△PCO ⇒AO =BO =CO .] 7.4
解析 由直线与平面垂直的性质定理知AB 中点到α距离为以3和5为上、下底的直角梯形的中位线的长.
8.①②③
解析 ①为直线与平面垂直的性质定理的应用,②为面面平行的性质,③为公理4的应用.
9.6
解析 由题意知CO⊥AB, ∴CO⊥面ABD ,∴CO⊥OD,
∴直角三角形为△CAO,△COB,△ACB,△AOD,△BOD,△COD. 10.证明 (1)∵ADD 1A 1为正方形, ∴AD 1⊥A 1D .
又∵CD⊥平面ADD 1A 1,∴CD⊥AD 1. ∵A 1D∩CD=D ,∴AD 1⊥平面A 1DC . 又∵MN⊥平面A 1DC , ∴MN∥AD 1.
(2)连接ON ,在△A 1DC 中, A 1O =OD ,A 1N =NC .
∴ON 綊12CD 綊1
2
AB ,
∴ON∥AM. 又∵MN∥OA,
∴四边形AMNO 为平行四边形,∴ON=AM .
∵ON=12AB ,∴AM=1
2
AB ,∴M 是AB 的中点.
11.证明
连接AG 并延长交BC 于D ,连接A′G′并延长交B′C′于D′,连接DD′,由AA′⊥α,
BB′⊥α,CC′⊥α,得AA′∥BB′∥CC′.∵D、D′分别为BC和B′C′的中点,
∴DD′∥CC′∥BB′,∴DD′∥AA′,
∵G、G′分别是△ABC和△A′B′C′的重心,
∴AG
GD
=
A′G′
G′D′
,∴GG′∥AA′,
又∵AA′⊥α,∴GG′⊥α.
12.证明∵M、N分别是EA与EC的中点,∴MN∥AC,
又∵AC⊂平面ABC,MN⊄平面ABC,
∴MN∥平面ABC,
∵DB⊥平面ABC,EC⊥平面ABC,
∴BD∥EC,四边形BDEC为直角梯形,
∵N为EC中点,EC=2BD,
∴NC綊BD,∴四边形BCND为矩形,
∴DN∥BC,
又∵DN⊄平面ABC,BC⊂平面ABC,
∴DN∥平面ABC,
又∵MN∩DN=N,
∴平面DMN∥平面ABC.
13.
(1)证明如图所示,由已知BC⊥AC,BC⊥CC1,得BC⊥平面ACC1A1.
连接AC1,则BC⊥AC1.
由已知,可知侧面ACC1A1是正方形,所以A1C⊥AC1.
又BC∩A1C=C,
所以AC1⊥平面A1BC.
因为侧面ABB1A1是正方形,M是A1B的中点,连接AB1,则点M是AB1的中点.
又点N是B1C1的中点,则MN是△AB1C1的中位线,所以MN∥AC1.故MN⊥平面A1BC.(2)解如图所示,因为AC1⊥平面A1BC,设AC1与A1C相交于点D,
连接BD,则∠C1BD为直线BC1和平面A1BC所成的角.
设AC=BC=CC1=a,则C1D=
2
2
a,BC1=2a.
在Rt△BDC1中,sin∠C1BD=C1D
BC1=
1 2
,
所以∠C1BD=30°,
故直线BC1和平面A1BC所成的角为30°.。