直线与平面的位置关系_课件

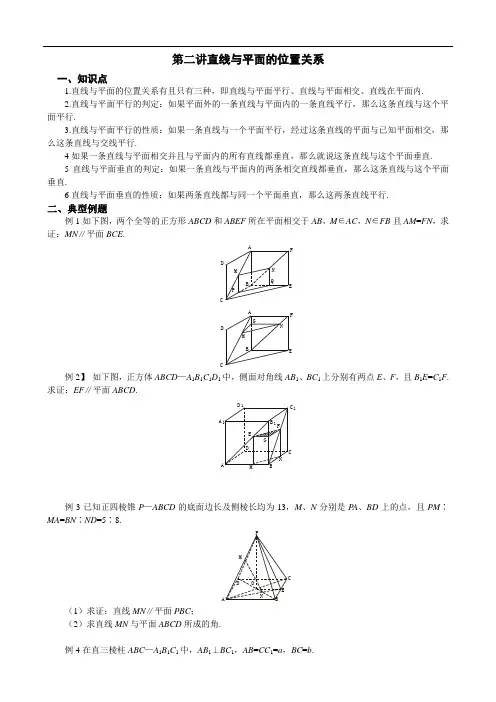
第二讲直线与平面的位置关系一、知识点1.直线与平面的位置关系有且只有三种，即直线与平面平行、直线与平面相交、直线在平面内.2.直线与平面平行的判定：如果平面外的一条直线与平面内的一条直线平行，那么这条直线与这个平面平行.3.直线与平面平行的性质：如果一条直线与一个平面平行，经过这条直线的平面与已知平面相交，那么这条直线与交线平行.4如果一条直线与平面相交并且与平面内的所有直线都垂直，那么就说这条直线与这个平面垂直. 5直线与平面垂直的判定：如果一条直线与平面内的两条相交直线都垂直，那么这条直线与这个平面垂直.6直线与平面垂直的性质：如果两条直线都与同一个平面垂直，那么这两条直线平行.二、典型例题例1如下图，两个全等的正方形ABCD 和ABEF 所在平面相交于AB ，M ∈AC ，N ∈FB 且AM =FN ，求证：MN ∥平面BCE .QAB CDMP FE NGA BCDM FE N例2】 如下图，正方体ABCD —A 1B 1C 1D 1中，侧面对角线AB 1、BC 1上分别有两点E 、F ，且B 1E =C 1F .求证：EF ∥平面ABCD .AA DBC BCD1111EFGMN例3已知正四棱锥P —ABCD 的底面边长及侧棱长均为13，M 、N 分别是P A 、BD 上的点，且PM ∶MA =BN ∶ND =5∶8.ABCD E O MNP（1）求证：直线MN ∥平面PBC ；（2）求直线MN 与平面ABCD 所成的角.例4在直三棱柱ABC —A 1B 1C 1中，AB 1⊥BC 1，AB =CC 1=a ，BC =b .AA CB BC E G F111（1）设E 、F 分别为AB 1、BC 1的中点，求证：EF ∥平面ABC ； （2）求证：A 1C 1⊥AB ；（3）求点B 1到平面ABC 1的距离.例5已知直线a ⊥平面α，直线b ⊥平面α，O 、A 为垂足.求证：a ∥b .Oα例6已知P A ⊥⊙O 所在的平面，AB 是⊙O 的直径，C 是⊙O 上任意一点，过A 点作AE ⊥PC 于点E ，求证：AE ⊥平面PBC .CABP.OE例7在直三棱柱ABC —A 1B 1C 1中，B 1C 1=A 1C 1，A 1B ⊥AC 1，求证：A 1B ⊥B 1C .AABBC CDD1111例8如图8—45, AB 是圆O 的直径,C 是圆上异于A,B 的任意一点,ABC PA 平面⊥,PC AF ⊥,求证PBC AF 平面⊥例9如图8—49, ABCD －1111D C B A 是正方形,求证BD C C A 11面⊥ 例10正方形ABCD －1111D C B A 中, 求()11BD 与面ABCD 所成角的正切值.(2)所成的角与面111D ABC BA ()所成角的正切值与面1113ACD D B例11.设有平面α、β和直线m 、n ，则m ∥α的一个充分条件是A.α⊥β且m ⊥βB.α∩β=n 且m ∥nC.m ∥n 且n ∥αD.α∥β且m β例12.设m 、n 是两条不同的直线，α、β、γ是三个不同的平面.给出下列四个命题，其中正确命题的序号是①若m ⊥α，n ∥α，则m ⊥n ②若α∥β，β∥γ，m ⊥α，则m ⊥γ ③若m ∥α，n ∥α，则m ∥n ④若α⊥γ，β⊥γ，则α∥βA.①②B.②③C.③④D.①④例13.一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是 A.异面 B.相交 C.平行 D.不能确定abcl αβγ例14设平面α∥平面β，A 、C ∈α，B 、D ∈β，直线AB 与CD 交于点S ，且AS =8，BS =9，CD =34，①当S 在α、β之间时，SC =_____________，②当S 不在α、β之间时，SC =_____________.例15设D 是线段BC 上的点，BC ∥平面α，从平面α外一定点A （A 与BC 分居平面两侧）作AB 、AD 、AC 分别交平面α于E 、F 、G 三点，BC =a ，AD =b ，DF =c ，则EG =_____________.例16在四面体ABCD 中，M 、N 分别是面△ACD 、△BCD 的重心，则四面体的四个面中与MN 平行的是________.三、练习题ABCDMN..1.“直线l 垂直于平面α内的无数条直线”是“l ⊥α”的 A.充分条件 B.必要条件 C.充要条件 D.既不充分又不必要条件2.给出下列命题，其中正确的两个命题是①直线上有两点到平面的距离相等，则此直线与平面平行 ②夹在两个平行平面间的两条异面线段的中点连线平行于这两个平面 ③直线m ⊥平面α，直线n ⊥m ，则n ∥α ④a 、b 是异面直线，则存在唯一的平面α，使它与a 、b 都平行且与a 、b 距离相等A.①②B.②③C.③④D.②④3.在正方形SG 1G 2G 3中，E 、F 分别是G 1G 2、G 2G 3的中点，D 是EF 的中点，沿SE 、SF 及EF 把这个正方 形折成一个四面体，使G 1、G 2、G 3三点重合，重合后的点记为G ，那么，在四面体S —EFG 中必有A.SG ⊥平面EFGB.SD ⊥平面EFGC.FG ⊥平面SEFD.GD ⊥平面SEF 4.在直四棱柱ABCD —A 1B 1C 1D 1中，当底面四边形ABCD 满足条件_____________时，有A 1C ⊥B 1D 1.（注：填上你认为正确的一种条件即可，不必考虑所有可能的情况）A AD DB BC C11115.设正方体ABCD —A 1B 1C 1D 1的棱长为1，则D D AA C CB B1111（1）A 点到CD 1的距离为________； （2）A 点到BD 1的距离为________；（3）A 点到面BDD 1B 1的距离为_____________； （4）A 点到面A 1BD 的距离为_____________； （5）AA 1与面BB 1D 1D 的距离为__________.6.两条直线a 、b 满足a ∥b ，b α，则a 与平面α的关系是 A.a ∥α B.a 与α相交 C.a 与α不相交 D.a α7.a 、b 是两条异面直线，A 是不在a 、b 上的点，则下列结论成立的是 A.过A 有且只有一个平面平行于a 、b B.过A 至少有一个平面平行于a 、b C.过A 有无数个平面平行于a 、b D.过A 且平行a 、b 的平面可能不存在8已知a 、b 为不垂直的异面直线，α是一个平面，则a 、b 在α上的射影有可能是①两条平行直线；②两条互相垂直的直线；③同一条直线；④一条直线及其外一点.在上面结论中，正确结论的编号是__________.（写出所有正确结论的编号）9.已知Rt △ABC 的直角顶点C 在平面α内，斜边AB ∥α，AB =26，AC 、BC 分别和平面α成45°和30°角，则AB 到平面α的距离为__________.10.如下图，四棱锥P —ABCD 的底面是边长为a 的正方形，侧棱P A ⊥底面ABCD ，侧面PBC 内有BE ⊥PC 于E ，且BE =36a ，试在AB 上找一点F ，使EF ∥平面P AD . A BC DEPGF11.如下图，设P 为长方形ABCD 所在平面外一点，M 、N 分别为AB 、PD 上的点，且MB AM =NPDN，求证：直线MN ∥平面PBC .ABCDMNPQ R。

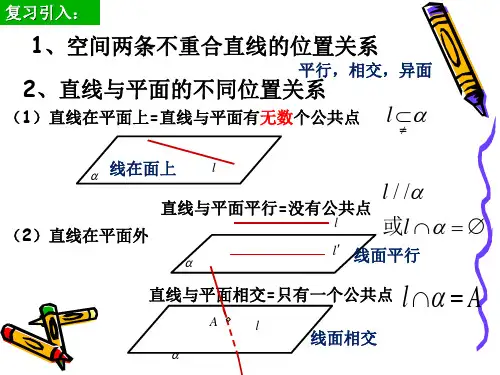
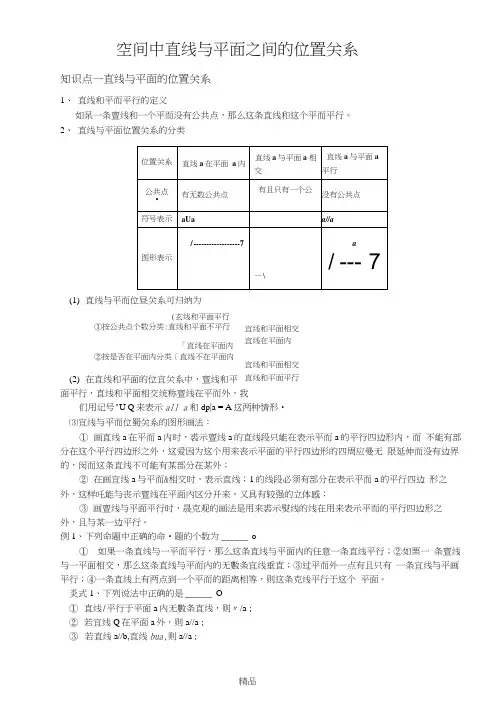
空间中直线与平面之间的位置关系知识点一直线与平面的位置关系1、 直线和平而平行的定义如杲一条亶线和一个平而没有公共点，那么这条直线和这个平而平行。

2、 直线与平面位置关系的分类(1) 直线与平而位昼关系可归纳为(玄线和平面平行①按公共点个数分类:直线和平面不平行「直线在平面内②按是否在平面内分类［直线不在平面内 (2) 在直线和平面的位宜关系中，亶线和平面平行，直线和平面相交统称亶线在平而外，我们用记号"U Q 来表示all a 和dp|a = A 这两种情形•⑶宜线与平而位蜀关系的图形画法：① 画直线a 在平而a 内时，裘示亶线a 的直线段只能在表示平而a 的平行四边形内，而 不能有部分在这个平行四边形之外，这爱因为这个用来丧示平面的平行四边形的四周应曼无 限延伸而没有边界的，闵而这条直线不可能有某部分在某外；② 在画宜线a 与平而&相交时，表示直线；1的线段必须有部分在表示平而a 的平行四边 形之外，这样吒能与丧示亶线在平面內区分开来，又具有较强的立体感；③ 画亶线与平面平行时，晟克观的画法是用来裘示熨线的线在用来表示平而的平行四边形之 外，且与某一边平行。

例1、下列命題中正确的命•題的个数为 ______ o① 如果一条直线与一平而平行，那么这条直线与平面内的任意一条直线平行；②如栗一 条亶线与一平面相交，那么这条直线与平而內的无數条宜线垂直；③过平而外一点有且只有 一条宜线与平画平行；④一条直线上有两点到一个平而的距离相等，则这条克线平行于这个 平面。

炎式1、下列说法中正确的是 ______ O① 直线/平行于平面a 內无數条直线，则〃/a ；② 若宜线Q 在平面a 外，则a//a ；③ 若直线a//b,直线bua,则a//a ；宜线和平面相交 宜线在平面内宜线和平面相交直线和平面平行④若直线a//b,直线bug 那么直线2就平行于平面a內的无數条宜线。

变式2、下列命题中正确的个数是（）①若直线1上有无数个点不在平而a内，则l//a②若直线1与平而a平行，则1与平而a内的任蕙一条直线都平行③如杲两条平行直线中的一条与一个平而平行，那么另一条也与这个平而平行④若直线1与平而Ot平行，则1与平而0C内的任意一条直线都没有公共点A.OB.lC.2D.3分析：如图2,图2我们借助长方体模型，AA,所在直线有无数点在平面ABCD外，但AA,所在直线与平面ABCP相交，所以命题①不正确；A IB I所在直线平行于平面ABCD, 显然不平行于BD,所以命題②不正确；所在直线平行于平面ABCP,但直线ABU平面ABCP.所以命题③不正确；1与平面0C平行，则1与a无公共点,1与平面«內所有直线都没有公共点，所以命题④正确. 卷案:B萸式3、若直线1上有两个点到平而oc的距离相等，讨论直线1与平而oc的位置关系.0 3解：直线1与平而oc的位亘关系有两种悄况（如图3）,直线与平而平行或賣线与平而相交. 例2、若两条相交直线中的一条在平面工內，讨论另一条直线与平而oc的位置关系.用符号语言表示为：若arib=A,bC：a,R>] aCZa或aAa=A.变式1、若两条异面直线中的一条在平而oc内，讨论另一条直线与平面oc的位虽关系.用符号语言表示为：若a与b异而则b//工或bAa=A.例3、若直线狄不平行于平而oc,且 y 则下列结论成立的是() A.a 内的所有直线与n 异而 B.oc 內的宜线与久都相交例如直线X B 与平而ABCD 相交，恵线AB 、CD 在平而ABCP 内，直线AB 与直线？/ B 相交，賣线CD 与直线工B 异面，所以A. B 都不正确；平面ABCP 內不存在与a 平行的 直线，所以应选D ・ 变式1.不在同一条直线上的三点A 、B 、C 到平而oc 的距离相等，且Aga,以下三个命题： ①AABC 中至少有一条边平行于oc;②AABC 中至多有两边平行于oc ；③ZLABC 中只可能有一条边与oo 相交.其中真命题畏 _______________ .其中真命题是①.萸式2、若賣线aCa,则下列结论中成立的个数是( (1) 00内的所有直线与a 异面 ⑵a 內的賣线与a 都相交 內不存在与次平行的直线A.OB.lC.2D.3分析：丁 直线 a (Za,/.a // a 或 ap|a=A.如图9,显然⑴⑵⑶(4)都有反例，所以应选A.咎案：A.知识点二直线与平面平行1、直线与平面平行的判定龙理：如杲平而外一条直线和这个平面内的一条直线平行，那么 这条直线和这个平而平行。