第八章 虚拟变量模型
- 格式:ppt
- 大小:730.50 KB
- 文档页数:56

第八章 包含虚拟变量的回归模型一、虚拟变量的基本含义通常在回归分析中,因变量不仅受一些定量变量的影响,而且还受一些定性变量的影响,比如性别、种族、婚姻状况等等。
为了在模型中反映这些因素的影响,需要把定性因素进行“量化”。
通常是引进人工变量完成。
通过定性因素的属性类别,构造取值为0或者1的变量,如、 1代表男性, 0代表女性; 1代表某人是大学毕业, 0代表某人不是大学毕业,这类取值为0,1的变量称为虚拟变量(dummy variable )。
虚拟变量与定量变量一样可用于回归分析。
事实上,一个回归模型的解释变量可以仅仅是虚拟变量。
解释变量仅是虚拟变量的模型称为方差分析模型( analysis-of-variance models ) (ANOVA)。
例1:1i i Y D i βα=++ε,其中Y 表示职工工资,。
10i D ⎧=⎨⎩,本科学历,非本科学历这个模型与我们前面讨论过的双变量模型类似,但这里的解释变量是虚拟变量。
1(0)i E Y D β==,1(1)i E Y D βα==+显然,1β表示非大学毕业生的平均初职年薪,1βα+表示具有大学学历职工的平均工资,α代表二者之差。
回归模型中可以有同时有虚拟变量以及定量变量。
例2:考虑是否上过大学和工龄作为职工工资的模型:12i i i Y X D i ββαε=+++Y ,表示职工工资,X表示工龄,D同上。
含虚拟变量的模型只要扰动项符合古典假定,仍用OLS方法估计模型。
注意:虚拟变量系数显著性检验的意义::0H 0α=;:1H 0α≠。
同学们思考:这个检验在上面两个例子中分别具有何实际意义?二、虚拟变量的引入模型的方式 1、加法方式上面考察的例子都是加法方式。
注意虚拟变量模型的几何意义:以上述例2考察。
例3:如果上述职工工资方程(例2)中,学历考虑三个层次:高中以下、高中、大学及以上。
该如何建模?引进两个虚拟变量:,1 1 0 D ⎧=⎨⎩高中其他2 1 0 D ⎧=⎨⎩大学及以上其他121222Y X D D ββαα=++++ε请同学们分析模型的含义。




第八章虚拟变量模型1. 回归模型中引入虚拟变量的作用是什么?答:在模型中引入虚拟变量,主要是为了寻找某(些)定性因素对解释变量的影响。
加法方式与乘法方式是最主要的引入方式,前者主要适用于定性因素对截距项产生影响的情况,后者主要适用于定性因素对斜率项产生影响的情况。
除此外,还可以加法与乘法组合的方式引入虚拟变量,这时可测度定性因素对截距项与斜率项同时产生影响的情况。
2. 虚拟变量有哪几种基本的引入方式? 它们各适用于什么情况?答:在模型中引入虚拟变量的主要方式有加法方式与乘法方式,前者主要适用于定性因素对截距项产生影响的情况,后者主要适用于定性因素对斜率项产生影响的情况。
除此外,还可以加法与乘法组合的方式引入虚拟变量,这时可测度定性因素对截距项与斜率项同时产生影响的情况。
3.什么是虚拟变量陷阱?答:根据虚拟变量的设置原则,一般情况下,如果定性变量有m个类别,则需在模型中引入m-1个变量。
如果引入了m个变量,就会导致模型解释变量出现完全的共线性问题,从而导致模型无法估计。
这种由于引入虚拟变量个数与类别个数相等导致的模型无法估计的问题,称为“虚拟变量陷阱”。
4.在一项对北京某大学学生月消费支出的研究中,认为学生的消费支出除受其家庭的每月收入水平外,还受在学校中是否得到奖学金,来自农村还是城市,是经济发达地区还是欠发达地区,以及性别等因素的影响。
试设定适当的模型,并导出如下情形下学生消费支出的平均水平:(1) 来自欠发达农村地区的女生,未得到奖学金;(2) 来自欠发达城市地区的男生,得到奖学金;(3) 来自发达地区的农村女生,得到奖学金;(4) 来自发达地区的城市男生,未得到奖学金。
解答: 记学生月消费支出为Y,其家庭月收入水平为X,则在不考虑其他因素的影响时,有如下基本回归模型:Y i=β0+β1X i+μi有奖学金1 来自城市无奖学金0 来自农村来自发达地区 1 男性0 来自欠发达地区0 女性Y i=β0+β1X i+α1D1i+α2D2i+α3D3i+α4D4i+μi由此回归模型,可得如下各种情形下学生的平均消费支出:(1) 来自欠发达农村地区的女生,未得到奖学金时的月消费支出:E(Y i|= X i, D1i=D2i=D3i=D4i=0)=β0+β1X i(2) 来自欠发达城市地区的男生,得到奖学金时的月消费支出:E(Y i|= X i, D1i=D4i=1,D2i=D3i=0)=(β0+α1+α4)+β1X i(3) 来自发达地区的农村女生,得到奖学金时的月消费支出:E(Y i |= X i , D 1i =D 3i =1,D 2i =D 4i =0)=(β0+α1+α3)+β1X i (4) 来自发达地区的城市男生,未得到奖学金时的月消费支出: E(Y i |= X i ,D 2i =D 3i =D 4i =1, D 1i =0)= (β0+α2+α3+α4)+β1X i5. 研究进口消费品的数量Y 与国民收入X 的模型关系时,由数据散点图显示1979年前后Y 对X 的回归关系明显不同,进口消费函数发生了结构性变化:基本消费部分下降了,而边际消费倾向变大了。




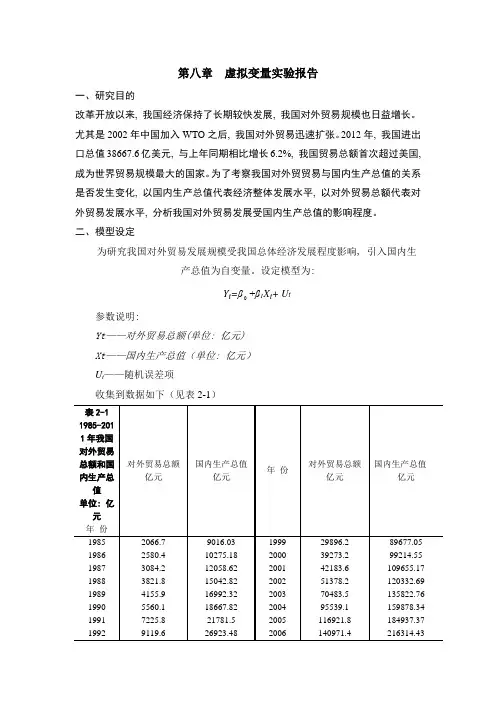
第八章虚拟变量实验报告一、研究目的改革开放以来, 我国经济保持了长期较快发展, 我国对外贸易规模也日益增长。
尤其是2002年中国加入WTO之后, 我国对外贸易迅速扩张。
2012年, 我国进出口总值38667.6亿美元, 与上年同期相比增长6.2%, 我国贸易总额首次超过美国, 成为世界贸易规模最大的国家。
为了考察我国对外贸贸易与国内生产总值的关系是否发生变化, 以国内生产总值代表经济整体发展水平, 以对外贸易总额代表对外贸易发展水平, 分析我国对外贸易发展受国内生产总值的影响程度。
二、模型设定为研究我国对外贸易发展规模受我国总体经济发展程度影响, 引入国内生产总值为自变量。
设定模型为:+β1X t+ U tY t=β参数说明:Yt——对外贸易总额(单位: 亿元)Xt——国内生产总值(单位: 亿元)U t——随机误差项收集到数据如下(见表2-1)1993 11271 35333.92 2007 166740.2 265810.31 1994 20381.9 48197.86 2008 179921.5 314045.43 1995 23499.9 60793.73 2009 150648.1 340902.81 1996 24133.8 71176.59 2010 201722.1 401512.8 1997 26967.2 78973.03 2011 236402 472881.56 1998 26693.823 73617.66322注: 资料来源于《中国统计年鉴》1986-2012。
为了研究1985-2011年期间我国对外贸易总额随国内生产总值的变化规律是否有显著不同, 考证对外贸易与国内生产总值随时间变化情况, 如下图所示。
图2-1 对外贸易总额(Y)与国内生产总值(X)随时间变化趋势图从图2-1中, 可以看出对外贸易总额明显表现出了阶段特征: 在2002年、2007年和2009年有明显的转折点。
