当前位置：文档之家 › 12动量矩定理wy

12动量矩定理wy

  • 格式：ppt
  • 大小：2.22 MB
  • 文档页数：76

下载文档原格式

  / 76

合集下载

12动量矩定理wy分析

12动量矩定理wy分析

第十二章：动量矩定理
§ 12-1 动量矩 § 12-2 动量矩定理 § 12-3 转动惯量 § 12-4 刚体绕定轴转动的微分方程
动量定理揭示了质点和质点系动量变化与外力主矢的关 系；质心运动定理揭示了质心运动与外力主矢的关系。但 它们无法描述质点系机械运动的全貌。
均质轮受外力作用而绕其质心O作定轴转 动，它有角速度和角加速度，但对于轮 的动量为：
mz
(F
i i
)
(1)
(i=1,2,….n)
将n个方程求和：
x
n
i 1
dmz (mivi ) dt
n i 1
mz
(Fie )
n i 1
mz
(F
i i
)
m1
mi Fei
y
mn m2
mi vi mj fij fji Fii
d
dt
mz (mivi )
mz (Fie )
dLz
dt
mz (Fie )
方向：垂直于r、mv所在的平面， 指向由右手螺旋法则判定。
(2)质点对固定轴的动量矩
M x (mv) [r mv]x y mv z z mv y M y (mv) [r mv] y z mv x x mv z M z (mv) [r mv]z x mv y y mv x
= ( -yi i +xi j )
y
mi
C ri
x
Lcr = ri mivri
= (xi i +yi j)mi( -yi i +xi j ) = k mi (xi2+yi2 ) = JC k = Lc
Lcz = JC
例题11-1. 边长为a 质量为m的正方体沿平直轨道滑动如 图所示。已知质心C的速度为v。求: (1) 正方体对轨道上 固定点O的动量矩; (2) 正方体的绝对运动对质心 C的动量 矩; (3) 正方体的相对运动对质心C的动量矩。
理论力学 12 动量矩定理

理论力学 12 动量矩定理


轴转动(zhuàn dòng)。已知均质杆 OA 长为 l ，质 C1 量为 m 1，均质圆盘 C 2 的半径为 r ，质量为 m 2，
试求复摆对 O 轴的动量矩。
A
C2 r
解： J O 的计算(jìsuàn)：
JO
1 12
m1
l
2
m1
l 2
2
1 2 m2
r2
m2
l
r
2
图 12-9
由几何关系知： r R h z
h 薄圆片对 y 轴转动惯量 d J y 为：
1 r2 dm 4
精品资料
dJ y
1 4
r 2dm
z 2dm
1 4
r2
z2
r 2dz
1
4
R4 h4
h
z 4
R2 h2
h
z 2
z2
dz
整个(zhěnggè)圆锥体对于 y 轴的转动惯量为：
J y
h 0
1 4
底圆直径的转动惯量。已知圆锥体质量为 M ，
z
底圆半径为 R ，高为 h ，如图12-6所示。 r
h z dz
解：把圆锥体分成许多(xǔduō)厚度为 d z 的薄圆片，该薄圆片的质量为
d m r2d z
为圆锥体的密度，r为薄圆片的半径。
O
y
R
x
图 12-6
圆锥体的质量为
M 1R2h
3
薄圆片对自身直径的转动惯量为
精品资料
12.1 转动惯量、平行(píngxíng) 轴定1理2.1.1 转动惯量
质点系的运动，不仅(bùjǐn)与作用在质点系上的力有关， 还与质点系各质点的质量其及分布情况有关。质心是描述质 点系质量分布的一个特征量，转动惯量(Moment of inertia)则 是描述质点系质量分布的另一个特征量。
理论力学 12.动量矩定理

理论力学 12.动量矩定理


得
LO mO (mvC ) rC mvC
对z轴的动量矩
Lz mz (mvC )
即：平动刚体对固定点（轴）的动量矩等于刚体质心的 动量对该点（轴）的动量矩。
2．定轴转动刚体 根据定义
Lz M z (mi vi ) mi ri ri mi ri2 mi ri2
PA PB d g dt r PA PB P/2
§8-3 动量矩守恒
动量矩定理：内力不会改变质点系的动量矩，只有外力才 能改变质点系的动量矩。 质点系的动量矩守恒 当 M O 0 时， LO 常矢量。
( e)
当 M z ( e ) 0 时，Lz 常量。 例如：花样滑冰运动员的高速旋转表演 ，J z 常量； 具有单个旋翼的直升飞机需要在尾部安装螺旋桨。
上式称为质点系对固定轴的动量矩定理。即质点系对任一固 定轴的动量矩对时间的导数，等于作用在质点系上所有外力对同 一固定轴之矩的代数和（外力系对同一轴的主矩）。 定理说明内力不会改变质点系的动量矩，只有外力才能改 变质点系的动量矩。 质点系的动量矩守恒
当 M O 0 时， LO 常矢量。
( e)
rC mvC ri mi v i
其中 LC ri mi v i 为质点系相对质心C的动量矩。 （注意：vi为质点的绝对速度。） 即 质点系对任意定点O的动量矩，等于质点系对质心的动量矩， 与将质点系的动量集中于质心对于O点动量矩的矢量和。
取固结于质心的平动参考系， 由速度合成定理，有
例8 水平圆板可绕z轴转动，其上有一质量为m的质点M作 半径为r的圆周运动，相对圆板的速度大小v0为常量。若圆板 对z轴的转动惯量为J，并且当M点离z轴最远时，圆板的角速 度为零。试求圆板的角速度与φ角的关系。轴的摩擦和空气阻 力略去不计。 解：取水平圆板和其上 的质点M为研究的质点系， 系统对z轴的动量矩守恒。 当质点M处于Mo位置，
动量矩定理

动量矩定理


( ) 2）若 ∑ m (F ) = 0 ，则 w = cos 2t 3）若 ∑ m (F ) = cos 2t ，则 ε = cos 2t 4）在一定的时间内，当 ∑ m (F ) 一定时， I
z z z
1）若 ∑ m z F ≠ 0 ，则刚体的转动状态一定发生变化。
z
越大 , 运动状态越大。
可见，转动惯量表现刚体转动状态改变的难易程度。因此说：转动惯量是刚 体转动时惯性的度量。 转微分方程可以解决两类动力学问题：
( )
( ) ( ) ( )
由于约束力通过 Z 轴，于是有：
n d (I z w ) = ∑ m z F i dt i =1
即：
Iz
N n d 2ϕ = m F 或 I ε = mz F i i ∑ ∑ z z dt 2 i =1 I =1
ቤተ መጻሕፍቲ ባይዱ
( )
这就是刚体定轴转动的微分方程，即刚体对定轴的转动惯量与角速度的乘 积，等于作用于刚体的主动力 对该轴之矩的代数和。 ．．． 由以上可知：
对于该点（或该轴）的动量矩保持不变，这种情形称为动量矩守恒。
4
理论力学讲义
例 2：已知：圆轮半径 r,量 m ，物块重 p 。求：物块加速度。 解：取整体研究，对 O 点的动量矩为
L0 = Iw +
p vr g
外力对 O 总的矩为 ∑ m0 F 由
( ) = pr
e
d (L0 ) = ∑ m0 F 得： dt p ar = pr g
I 2 a / R = Nr2 − RT p a =T − p g I 1ia / R = M − Nr2 / i
⎫ ⎪ ⎬ ⎪ ⎭
未知量 a, T , Nr2 可求解：解之可得：
第12章 动量矩定理

第12章 动量矩定理

i 1 i 1
n
n
Lo Lx i Ly j Lz k
其中， Lz ( LO ) z
z
M (m v )
i i
质点（系）对 O点的动量矩在通过该点的 任意轴上的投影，等于质点（系）对该轴的动
量矩。
已知A、 B两物块的质量分别为 mA、 mB ，它们的 速度为v，轮的质量不计，半径为 R。求系统对轮 心 O的动量矩。 v O O B A
i 1
n
(i)
d ri mi vi n (e) 0 ，于是 ri Fi dt i 1
dLo dt
M
i 1
n
o
( Fi
(e)
)
质点系动量矩 定理的投影式
4、质点系动量矩守恒
dLx n (e) M x ( Fi ) dt i 1 n dL y (e) M y ( Fi ) dt i 1 n dLz (e) M z ( Fi ) dt i 1
J z mi R R
2 2
mi mR z
R
2
mi
3、均质圆板对中心轴的转动惯量 dr
以薄圆环作为质量微元
r O
O
R
d m 2 r d r S
R
2
其中
S m/ R
4
2
R J z 2 r S d r r 2S 4 0
1 2 J z mR 2
1、质点的动量矩定理
d d dr d MO (m v ) ( r m v ) m v r (m v ) dt dt dt dt
dr d ( m v ) F ，且 O为定点， v 根据动量定理 dt dt
12动量矩定理

12动量矩定理


图12.7 钟摆
第12章 动量矩定理
12.1 转 动 惯 量
【例12.5】 匀质圆盘与匀质杆组成的钟摆如图12.7所示。已知圆盘质量m1， 直径d，杆的质量m2，长l，试求钟摆对悬挂轴O的转动惯量J0。
解：钟摆由匀质杆和匀质盘组成，所以有 = JO JO杆 + JO
其中
JO
=J c
+
m1
l
+
d 2
平方的乘积，即
12.7
J=z J zc + md 2
(12.7)
第12章 动量矩定理
12.1 转 动 惯 量
证明：如图12.5所示，设刚体总的质量为m，轴zc通过质心C，z与zc平行且 相距为d。不失一般性，可令y与yc重合，在刚体内任取一质量为mi的质点Mi,它 至zc轴和z轴的距离分别为ric和ri。刚体对于z、zc轴的转动惯量分别为
12.9
第12章 动量矩定理
12.1 转 动 惯 量
【例12.4】 质量为m，长为l的匀质杆如图12.6所示，求杆对yc的转动惯量。
解：由例12.1知
Jy
=
1 ml2 3
,根据平行轴定理式(12.7)有
J yc
=J y
−
md 2
=1 ml2 3
−
m
l
2
2
=1 12
ml 2
12.10
图12.6 匀质杆
在工程问题上，计算刚体的转动惯量时，常应用下面公式
12.3
第12章 动量矩定理
12.1 转 动 惯 量
Jz
=
mρ
2 z
(12.2)
ρ 其中m为整个刚体的质量， z 为刚体对z轴的回转半径，它具有长
第十二章 动量矩定理

第十二章 动量矩定理


Lz=Jzω
§2 动量矩定理
一、质点的动量矩定理
设质点质量为m， 受力F， MO(mv) 动量mv，定坐标系Oxyz ， 根据质点的动量定理 z
F
B
mv
r
o A y
MO(F)
d (mv ) F dt
等式两边同时与矢径r作矢量积， 即 x
d (mv ) r F r dt
MO(F)
?
d (mv ) r F 为求等式 r 左边项，先来看 dt d (r mv ) dr mv r d (mv ) dt dt dt v ( r d ( v mv∵O为定点！)mv ) dt MO(mv) =0
第十二章
动量矩定理
z
§1 动量矩的概念
一、质点的动量矩
F r
o
B A m
y
回顾： 力对点的矩 Mo(F)= r×F 若 r=xi+yj+zk F=Fxi+Fyj+Fzk
则 i M o (F ) x Fx
j y Fy k z Fz
MO(F)
x
大小：│Mo(F) │ =2S△OAB
方向：按右手螺旋规则定。
[Mo(mv)]z= M z(mv)
代数量
• 动量矩的量刚为 ML2T－1 （kg· 2/S） m
二、质点系的动量矩
质点系对固定点O的动量矩等于各质点对同 一点O的动量矩的矢量和（即质点系动量对点O 的主矩）：
对定点
Lo M o (mi vi )
i 1
n
矢量
质点系对固定轴z的动量矩等于各质点对同一 轴z的动量矩的代数和，即
vC
C
Lo = M o(Mvc)
12.动量矩定理

12.动量矩定理


例二 . 电动绞车提升一质量为m 的物体 , 在其主动轴上作用有一个力偶其矩 为M . 已知主动轴齿轮和从动轴齿轮各自对其转轴的转动惯量分别为 J1 和 J2 . 传 动比 z2 : z1 = i ; 从动轮上的鼓轮半径为R . 不计绳索的质量和各处摩擦. 求: 重物的加速度.
FAy FN y
A M J1
动量定理描述了物体的运动和力之间的关系, 但并不完整. 在运用动量定理时, 不能求力偶或 力矩,运动量也不能涉及角速度和角加速度. 而动量矩定理描述了质点系或刚体的运动 和力矩之间的关系. 这两个定理一并可完整地 描述外力系与受力体运动之间的定量关系.
§12 – 1 质点和质点系的动量矩
1. 质点的动量矩
v
M
O
解: 取整个系统为研究对象, 受力及运动分析如图
Fy
θ R ω
v
M
O
Fx
m1 g
由对O点的动量矩定理 d ( J O m 2 vR ) m 2 gR sin M dt a J O m 2 R a M m 2 gR sin R MR m 2 gR 2 sin a J O m2 R 2
c VC hC Βιβλιοθήκη R hAR hA vB v A 7.14km / s b
例二. 质量为m 的小球 悬挂在一绳索下端且以匀速率在水平面内作圆周运动. 试分析小球对O, A 两点的动量矩及其守恒问题. A
解 : 取小球分析 M A (m v ) r m v M O (m v ) R m v M A (F ) r mg 而 M O ( F ) R m g R T R (m g T ) 0 M O (m v ) 常矢量。 小球对o点的动量矩守恒 . M A (m v ) 常矢量. 小球对A点的动量矩不守恒 .
理论力学第12讲动量矩定理

理论力学第12讲动量矩定理

第四章 动量矩定理
一、质点动量矩
§4-1
二、质点系的动量矩 1. 对点的动量 矩
动 量 矩
质点系内各质点对某点 O 的动量矩的矢量和，称为这质点系对该点 O 的动量主矩或动量矩。用 LO 表示，有
LO = ∑MO(mivi) =∑r mivi
2. 对轴的动量 矩 类似的可得质点系对各坐标轴的动量矩表达式
思考 题 1
一半径为R、质量为m1的匀质圆盘与一长为l、质量为m2 的匀质细杆相固连，以角速度 在铅直面转动。试求该系统
对O轴的动量矩。
解: 系统做定轴转动，该系统对O轴的
动量矩
1
2

2
l
LO J O [ m2l m1 R m1 ( R l ) ] 3 2
2
1
C
R
顺时针。
将上式投影到固定坐标轴系上，注意到导数的投影等于投影的导数，则得
dL x dt dL y dt dL z dt M x ( Fi
(e)
) Mx ) My ) Mz
M y ( Fi M z ( Fi
(e)
有 结 论
(e)
质点系对某固定轴的动量矩随时间的变化率,等于作用于质点系的全部外力
动 力 学
动量矩定理
第四章 动量矩定理
第四章 动量矩定理
动量定理不能用于研究直升飞机姿态动力学
第四章 动量矩定理
第四章 动量矩定理
几个实际问题
谁最先到 达顶点
？
第四章 动量矩定理
实际问题
第四章 动量矩定理
几个实际问题
直升飞机如果 没有尾翼将发生 什么现象
？
第四章 动量矩定理
第四章 动量矩定理
十二章动量矩定理

十二章动量矩定理


F mv
M0(F)
o
Ｑ
y
x
由牛顿第二定律
m
dv dt
F
d dt
(mv)
F
r
d dt
(mv)
r
F
d (r mv) r d(mv) dr mv
dt
ห้องสมุดไป่ตู้
dt dt
理论力学电子教程
第十二章 动量矩定理
d (r mv) r F dt
M0(mv) m0(F)
理论力学电子教程
第十二章 动量矩定理
C
m2
IOZ M
式中
M
m1
O
IOZ
1 3
m1L2
1 2
m2
r
2
m2L2
理论力学电子教程
第十二章 动量矩定理
代入已知值得：
IOZ
1 10 0.32 3
1 40 0.152 2
40 0.32
4.35kg m2
M 20 4.6rad / s2
IOZ 4.35
理论力学电子教程
第十二章 动量矩定理
dt
M y (mv)]
my (Fe )
d [
dt
M z (mv)]
mz (Fe )
理论力学电子教程
第十二章 动量矩定理
【典型题精解】
例12-1 滑块Ａ，Ｂ质量分别为２Ｋｇ，0.5Ｋｇ，用长１
米的绳连接，在水平光滑滑竿上滑动，绳和竿的质量不计。
竿绕铅垂轴转动，轴的摩擦也不计。当 rA 0.6m 时，滑块 Ａ以速度０.４ｍ／Ｓ沿竿向外运动，竿的角速度 0.5rad / s
求此时竿的角加速度。
1m
B rB
动量矩定理12章

动量矩定理12章


)2
0
z
B
D
例： 均质圆盘，其绕轴O的转动惯量为J ，可绕通
过其中心的轴无摩擦地转动，另一质量为 m2
的人由 B 点按规律 s 1 at 2 沿距 O 轴半径
为 r 的圆周运动。初始2时，圆盘与人均静止。
求圆盘的角速度与角加速度。
解： 圆盘与人一起 —— 研究对象
受力分析： M z (Fi ) 0
大小： LO mv d
方向：LO mv, LO r
LO=MO(mv)
B
mv α
指向：按右手法则确定
几何表示： LO mv d 2OAB的面积
O
rA
d
y
x
对轴的动量矩
类似于力对点之矩与力对轴之矩的关系： MO (F ) x M x (F ) yFz zFy
质点的动量 mv 对 x 轴之矩 ：
§12 –1 质点和质点系的动量矩 z
一、质点的动量矩
对点的动量矩 力对点O之矩：MO (F ) r F
MO(F)
B
F α
质点的动量对点O之矩
—— 质点 的动量对O点的动量矩 LO MO (mv) r mv
—— 固定矢量
O
rA
d
x
y
—— 度量质点绕某一点转动运动强弱的运动特征量
z
LOz (JO m1r12 m2r22 )
(b)
外力主矩仅由重力 m1g 和 m2g 产生，有
m0g
A
B
v2 m2g
v1 m1g
MOz (m1r1 m2r2 )g
(c)
(b)
例题
dLOz dt
M Oz
(a)
LOz (JO m1r12 m2r22 )

理论力学12—动量矩定理.ppt


dt v2 r2 cos 2 LCDcd qV dt v1r1 cos 1 LABab qV
应用动量矩定理
dLz (e) Mz dt
qV (v2 r2 cos 2 v1r1 cos 1 ) Mz
M z nM z qV (v2 r2 cos 2 v1r1 cos1 )
z
A
l
C
a
Lz1 Lz 2
0
a
B
l
Lz1 2(ma0 )a 2ma 0
2
D
Lz 2 2m(a l sin )2 2ma20 2m(a l sin )2 a2 0 2 (a l sin )
显然，此时的角速度＜ 0。
z
A
l
C
a


质点系对 某固定轴的动 量矩对时间的 导数，等于作 用于质点系的 外力对于同一 轴的矩的代数 和。
12.2.3 动量矩守恒定理
1. 质点动量矩守恒定律 如果作用在质点上的力对某定点(或定轴) 之矩恒等于零，则质点对该点(或该轴)的动量 矩保持不变。
2. 质点系动量矩守恒定律
当外力对于某定点(或某定轴)的主矩等于 零时，质点系对于该点(或该轴)的动量矩保持 不变。
(e)
FOy O FOx u
va u v LO mva r mvr 0 LO m(u v)r mvr 0 u u va v 2 2
由上可知，人与重物 A 具有相同的的速度，此速度等 于人相对绳的速度的一半。如果开始时，人与重物 A 位于同一高度，则不论人以多大的相对速度爬绳，人 与重物A将始终保持相同的高度。
O
M z (mv) mvl ml 2

第十二动量矩定理-资料


Jy

m 12
(b 2
c2)
y
1 (b 2 c 2 ) 12
abc
JZ

m 12
(a 2

b2)
Jy

m 12
a2
Jy

m 12
b2
z
1 (a 2 b2) 12
x 0 .289 a
y 0 .289 b
abh
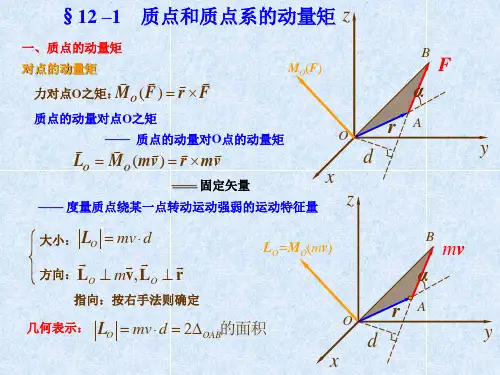
§12-5 质点系相对于质心的动量矩定理
1．对质心的动量矩
L z M z(m iv i) m iv ir i
m i riri m iri2
转动惯量
Jz miri2
Lz Jz
§12-2 动量矩定理
1．质点的动量矩定理
设O为定点,有
ddtMO(mv)ddt(rmv)
drmvrd(mv)
dt
dt
其中:
d (mv) F dt d r v （O为定点） dt
例12-3：已知 m, J O , m 1 , m 2 ,r1 , r2 ,不计摩擦.
求:（1）
（2）O处约束力 F N
（3）绳索张力 F T1 ，F T 2
解： (1) L O J O m 1 v 1 r 1 m 2 v 2 r 2
(JOm 1r12m 2r2 2)
dt
d A 称面积速度.
dt
面积速度定理：质点在有心力作用下其面积速度守恒.
例12-4：两小球质量皆为m,初始角速度 0 求：剪断绳后, 角时的.
解： 0 时,
Lz12ma 0a2m2 a0
0 时,
由
Lz2 2m (alsin )2

第12章 动量矩定理


§12-3 动量矩定理
例 题 5
两个鼓轮固连在一起，其总质量是 m，对水平转轴O的
转动惯量是 JO ；鼓轮的半径是 r1 和 r2 。绳端悬挂的重物 A和 B 质量分别是 m1 和 m2 ，且 m1 > m2。试求鼓轮的角 加速度(与例12－1类似）。
r1 r2
w
A
B
§12-3
动量矩定理
例 题 5
解: 1、选系统（含鼓轮，重物 A , B）为研究对象
2、运动分析 设鼓轮的角速度为w， 物 A的速度：v1= r1w 物 B的速度：v2= r2w
2
y
FO
r1 r2
w
mg
3、受力分析 重力 mg，m1g ， m2g 轴O处约束力 FO
LOz ( J O m1r1 m2 r2 )w
2
v1 A m1 g v2
y
m
w
C
平面运动＝随C平动＋绕C转动
ri
O
rC
x
LC J C ωk , 为动量偶
第12章 动量矩定理
§12-2 刚体对轴的转动惯量
§12-2 刚体对轴的转动惯量
z
2-1 定义
J z ri mi
2
ri
vi
mi
i
均质连续体：
w
O x
y
J z M r dm
2
单位：kg· m2
3、 质点系动量矩守恒定理
若
e M O ( Fi ) 0 e M z ( Fi ) 0
dL O e MO dt
则 LO 常矢 则 Lz 常量
即：当质系所受合外力对某定点（或某定轴）的 矩为零，则质系对该点（或该轴）的动量矩保持 不变 —— 质系动量矩守恒定律。

第12章动量矩定理


n
质点系对O点的动量矩在通过O点任一轴上的投影等于 质点系对该轴的动量矩。
L L
O z
zபைடு நூலகம்
4
3．平动和转动刚体的动量矩
a 、刚体平动时可将其全部质量集中于质心，做为一个质点
计算动量矩。 L M (mv ) O O C
Lz M z (mvC )
b、刚体绕定轴转动 n n Lz M z mi vi mi vi ri
i 1
z
mi ri ri mi ri2
i 1
n
i 1
O’
ri mi
mi v i
定义：刚体对z轴转动惯量：
J z mi ri
则：
2
反映质量关于z的分布情况。
Lz J z
5
绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的
转动惯量与转动角速度的乘积。
6
d [ M O ( mv )] M O ( F ) 1．质点的动量矩定理 dt 将此式在通过固定点O的三个直角坐标轴上投影，得
d [ M x ( mv )] M x ( F ) dt d [ M y ( mv )] M y ( F ) dt d [ M z ( m v )] M z ( F ) dt
0——称角振幅
周期
T 2
JO mga
——称初相位
19
例12-7：已知飞轮对O的转动惯量JO，以角速度0绕O轴转动，制动时，
闸块给轮正压力FN，已知闸块与轮之间的动滑动摩擦系数为f，轮半
径为R，轴承的摩擦忽略不计，求制动所需时间。
R O

20
例12-7：已知飞轮对O的转动惯量JO，以角速度0绕O轴转动，制动时，
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Lc
Jc
1 2
mR 2
1 2
mRvc
vc R
Jc
1 mR2 2
D
思考:对速度瞬心 D 的动量矩 ？
答案:
LD J D JC mR 2 或
LD LC mvC R JC mvC R
§ 12-3 动量矩定理
一、质点的动量矩定理
MO(mv)=r mv
将上式两端对时间求一阶导数，得：
dt
M z (F)
——质点系动量矩定理及其守恒
◆ 对某固定点O的动量矩定理：
dLO
dt
mO F e
质点系内力不能改变质点系的动量矩， 只有外力才是系统动量矩改变的原因。
即：质点系对某固定点O 的动量矩Lo 对时间的导数，等于作用于该 质点系的所有外力对于同一点之矩的矢量和（即外力系对O 点的主 矩）。
直杆OA和质量为 m 半径为 R的 均质园盘 A在 A点刚接 , 如图所 示.求系统对垂直于图面且过 O 点的轴的转动惯量。
O A
R
解:
JO = JOA + J盘
J OA
1 3
ml 2
O
J 盘 J A m (OA)2
1 mR2 m (OA)2
2
A
1 mR2 ml 2
R
2
JO
4 3
ml2
LO M BvB R M AvA R 0
B
vB vA
VA
又因为二人在同一高度上，从静止开始向上爬，
MAg
所以二人同时到达顶端。
VB MBg
——应用举例 例七 已知：水平匀质圆台重G ，半径为R ，无摩擦地绕通 过其中心的铅直轴OZ 转动。重为P 的人以不变的相对速度
u 在圆台上行走，且与OZ轴的距离 始终保持为r 。初始时圆台与人均
D
JO
1 3
ml 2
13 12
ml 2
17 12
ml 2
例题11-1. 边长为a 质量为m的正方体沿平直轨道滑动如 图所示。已知质心C的速度为v。求: (1) 正方体对轨道上 固定点O的动量矩; (2) 正方体的绝对运动对质心 C的动量 矩; (3) 正方体的相对运动对质心C的动量矩。
C
v
O
解: 建立直角
因此，应分别选取两轮为研究对象。
M
r1
O1
r2 O2
解：1、选O1轮为研究对象， 受力分析
M
Y1
O1
α1
x1
P1
Pt Pn
根据刚体的定轴转动微分方程：
J11 mo1 (Fie ) M Pt r1(1)
M r1
O1
Pn Pt
r2 O2
2、选O2轮为研究对象，受力分析 根据刚体的定轴转动微分方程：
均质轮受外力作用而绕其质心O作定轴转 动，它有角速度和角加速度，但对于轮 的动量为：
P mvC mvO 0
不能用动量定理来描述轮绕其质心的定轴转动。
§ 12-1 动 量 矩
(1) 质点的动量矩
mv
质量为m的质点A ,t 时刻动量 为mv, O为空间任一固定点,
MO(mv)
d
A
则mv 对O点的矩定义为质
约束反力T（用动量定理）。
O
A B
解: (1) LO = LOO + LOA + LOB
LOO = 0.5M(2r)2 = 2Mr2
vA = vB = R
O
LOA = m1R vA = 4m1r2 LOB = m2R vB = 4m2r2
vB
A
LO = 2Mr2 + 4m1r2 + 4m2r2
第十二章：动量矩定理
§ 12-1 动量矩 § 12-2转动惯量 § 12-3动量矩定理 § 12-4 刚体绕定轴转动的微分方程 § 12-5 刚体平面运动微分方程
动量定理揭示了质点和质点系动量变化与外力主矢的关 系；质心运动定理揭示了质心运动与外力主矢的关系。但 它们无法描述质点系机械运动的全貌。
所以
Lz
Jz
Q 2g
(R2
e2 )
例题11-8. 质量均为m长度
O
均为 l 的直杆OD和AB在D点
刚接,且AD=DB,如图所示。
求系统对垂直于图面且过 O A
B
点的轴的转动惯量。
D
O 解: JO = JOD + JAB
JOD
1 3
ml 2
A
B
J
AB
1 12
ml 2
m
(OD)2
13 12
ml 2
即：当人顺时针方向走动后，圆台角速度转向为逆时针。
39
3、利用动量矩定理或刚体定轴转动微分方程的解题步骤： （1）选择合适的研究对象，分析研究对象所受外力，画出
受力图，计算出该力系对相应轴的力矩之和。 （2）分析研究对象的运动情况，计算相应运动量间关系。 （3）利用动量矩定理或刚体定轴转动微分方程建立动力学
O
r
点的动量矩:
MO(mv)=r mv
动量矩是一个矢量.
大小： MO (mv) r mv r mv sin mv d
方向：垂直于r、mv所在的平面， 指向由右手螺旋法则判定。
(2)质点对固定轴的动量矩
M x (mv) [r mv]x y mv z z mv y M y (mv) [r mv] y z mv x x mv z M z (mv) [r mv]z x mv y y mv x
则 Lo ＝ 常矢量； 则 Lz ＝ 常量
即：如果作用于质点系上的所有外力对某固定点（或固定轴） 的矩的矢量和（或力矩的代数和）恒等于零，则质点系对 该点（或该轴）的动量矩保持不变，称为质点系动量矩守 恒定律。
例题11-10. 质量为M 半径为2r 的 均质滑轮绕固定轴O转动,质量分 别为m1和m2的物体A和B悬挂于 定滑轮上,如图所示。求:(1) 定滑 轮的角加速度; (2)定滑轮所受的
实验方法测定转动惯量
工程中，对于几何形状复杂的物体，常用实验方法测定其转动惯 量。例如，欲求曲柄对于通过点 O 的水平轴的转动惯量，可将曲柄 在点 O 悬挂起来，并使其作微幅摆动，由于摆动周期与转动惯量的 大小有关，即
T 2 J
mgl 则转动J 惯量T可2m按g照l下式计算 :
4 2
例题11-6 质量为 m 长度为 l 的均质
——应用举例 因为初始时，系统静止，则 Lz1 ＝0, 人走动后，圆台开始转动， 假设ω 为顺时针方向，则：
注意：第一项表示？第二项表示？
38
——应用举例
（注：在求人对 Z 轴的动量矩时,一定要用绝对速度！） 由动量矩守恒定律，有：
Lz2 0
即
GR2 2g
pr 2 g
pur g
0
立即解出：
式中“－”号说明假设ω 与实际转向相反。
CZ
1 12
ML2
M----杆的质量
矩形板 b
细圆环 薄圆板
y
C
a z
r
z r
J
x
1 12
M
a2
X
ห้องสมุดไป่ตู้
J
y
1 12
Mb2
J z Mr 2
Jz
1 Mr2 2
圆柱体
z r
Jz
1 Mr 2 2
空心圆盘
内圆m，外圆M。 r
R
Jz
1 2
MR2
1 2
mr2
注意：1、转动惯量具有可加性； 2、不易计算的物体采用实测法。
静止。
求: 当人走动时，圆台的角速度ω。
36
——应用举例
解：取研究对象：“人—圆台”系统 分析外力
如图：G，P——重力
轴承约束反力： FAX ,FAY ,FAZ FBX ,FBY
从受力图可见： ∑mz ( F e ) ≡ 0
(∵所有外力均平行于Z 轴或通过Z 轴)
所以系统对Z 轴的动量矩守恒。
即： Lz ＝常量 （即 Lz1 ＝ Lz2） 37
Miri2
令
miri2 JZ
LZ=Jz •ω
其中： JZ称为刚体对转轴的转动惯量。 ω为刚体转动的角速度。
例题11-3. 有对称面的刚体在 平行于对称面的平面内作平面 运动,角速度为。求:刚体对过 质心且垂直于对称面的轴的动 量矩。
C
解: 取坐标如图
vri = ri =k(xi i +yi j)
1 2
mR2
例题11-7. 均质偏心圆轮重Q， 偏心距OC=e，绕过O点且与图 平面垂直的Z轴转动，某瞬时其 角速度为。求:在该瞬时圆轮对 Z轴的动量矩。
O
C R
解：因为圆轮绕定轴转动，所以：
LZ=Jzω
根据平行移轴定理：J z
J cz md 2
1 mR 2 m OC 2 2
Q (R2 e2) 2g
B
= 2r2 (M + 2m1 + 2m2)
计算外力对O点的主矩
YO
Mze = (m1 - m2)gR
O
XO
= 2r(m1 - m2)g
Mg
dLz dt
M
e z
vB
A
B
2r2(M + 2m1 + 2m2) = 2r(m1 - m2)g m1g
(m1 m2)g
m2g
r(M 2m1 2m2)
O
分别抓住缠绕在定滑轮O上的绳子
的两端，在同一高度上，从静止
开始向上爬，试分析比赛结果。
A
B 动量矩守恒定律
分析：
把轮、绳和两人看作是一质点系，受力分析： Yo
MO (Fie ) M AgR M B gR 0