当前位置：文档之家 › 工程力学-材料力学-第12章动量矩定理(华蕊)

工程力学-材料力学-第12章动量矩定理(华蕊)

  • 格式：pptx
  • 大小：1.55 MB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

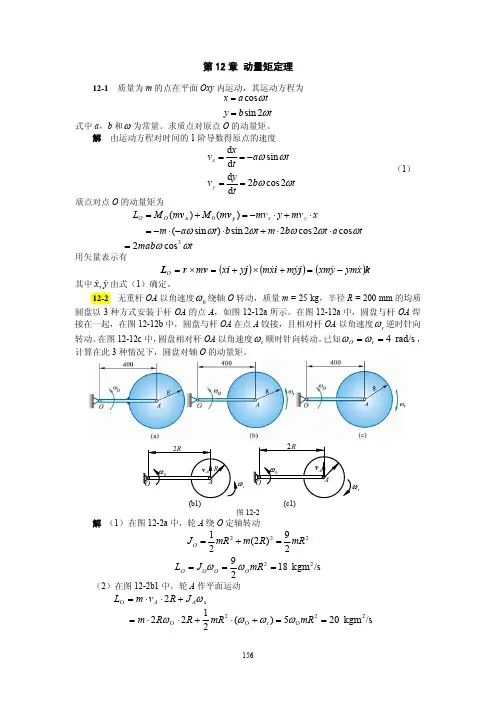
工程力学-材料力学-第12章动量矩定理

工程力学-材料力学-第12章动量矩定理
•注意：内力不能改变质点系的动量矩。
•
例12-3 •已知：m1，r，k ，m2 ，R，
•求：弹簧被拉长s时，重物m2的加速度a2 。 •解 •选系统为研究对象,受力分析如图 •设：塔轮该瞬时的角速度为ω，则
•解得：
•
3．动量矩守恒定律
•若
，则 常矢量；
•若
，则 常量。
•
§12-3 刚体绕定轴转动的微分方程 •主动力： •约束力：
•
例12-8 •已知：l，m，θ=60°。求：1. αAB；2. FA • 解：绳子刚被剪断，杆AB作平面运
动，受力如图，根据平面运动微分 方程
• 补充运动学方 程
• 在y轴方向 投影
•
例12-9 •已知：如图r，m， m1。求：1. aA；2. FAB ；3. FS2 • 解：分别以A、B、C为研究对象
•其中： • (O为定点)
•
质点的动量矩定理
•因此 •称为质点的动量矩定理：质点对某定点的动量矩 对时间的一阶导数，等于作用力对同一点的矩。
•投影式：
•
2. 质点系的动量矩定理 •对第i个质点有 ： •对n个质点有：
• 由于
•得
•
2. 质点系的动量矩定理
•称为质点系的动量矩定理：质点系对某定点O的动量 矩对时间的一阶导数，等于作用于质点系的外力对于 同一点之矩的矢量和。 •投影式：
•2. 选轮2为研究对象
•积分
•
§12-4 质点系相对于质心的动量矩定理 •1．对质心的动量矩 •如图，以质心C为原点，取平移坐标系Cx’y’z’。 •质点系相对质心C为的动量矩为：
•由于 •得 • 质点系相对质心的动量矩，无论是以相对速度计算还是
以绝对速度计算，其结果都相同。

动量矩定理

动量矩定理

θ 2 = 21°30′ 。设空气密度 ρ = 1.16 kg/m 3 ，求这 1 级叶轮的转矩。
解 取气流进行研究，气流以 v1 速度进入气道，一段时间后以 v2 速度流出，用动量矩定理对转动轴 O 的投影式，有
dLO =M dt
参照教材例 12-2 解的结果得
M =ρ
即
qV ⎛ D2 D ⎞ v2 cosθ 2 − 1 v1 cosθ 1 ⎟ ⎜ 60 ⎝ 2 2 ⎠
2R
2R
vA R
ω0
O
ω0
ωr
O
(c1) 图 12-2
vA
A
A (b1)
ωr
解 （1） 在图 12-2a 中，轮 A 绕 O 定轴转动
1 9 J O = mR 2 + m(2 R) 2 = mR 2 2 2 9 LO = J Oω O = ω O mR 2 = 18 kgm 2 /s 2
（2）在图 12-2b1 中，轮 A 作平面运动
h R
（1）
h m1 gR − M f t12 ⋅ = R J A + m1 R 2 2
160
将第 1 次试验时 m1，t1 替换为第 2 次试验时 m2，t2 得
2 h m2 gR − M f t 2 = ⋅ R J A + m2 R 2 2
（2）
式（1） 、 （2）联立，解得
J A = 1060 kg ⋅ m 2
LO = m ⋅ v A ⋅ 2 R + J Aω a 1 = m ⋅ 2 Rω O ⋅ 2 R + mR 2 ⋅ (ω O + ω r ) = 5ω O mR 2 = 20 kgm 2 /s 2
156
（3）在图 12-2c1 中，轮 A 绕 O 作圆周曲线平移

第12章 动量矩定理

第12章 动量矩定理
i 1 i 1
n
n
Lo Lx i Ly j Lz k
其中， Lz ( LO ) z
z
M (m v )
i i
质点（系）对 O点的动量矩在通过该点的 任意轴上的投影，等于质点（系）对该轴的动
量矩。
已知A、 B两物块的质量分别为 mA、 mB ，它们的 速度为v，轮的质量不计，半径为 R。求系统对轮 心 O的动量矩。 v O O B A
i 1
n
(i)
d ri mi vi n (e) 0 ，于是 ri Fi dt i 1
dLo dt
M
i 1
n
o
( Fi
(e)
)
质点系动量矩 定理的投影式
4、质点系动量矩守恒
dLx n (e) M x ( Fi ) dt i 1 n dL y (e) M y ( Fi ) dt i 1 n dLz (e) M z ( Fi ) dt i 1
J z mi R R
2 2
mi mR z
R
2
mi
3、均质圆板对中心轴的转动惯量 dr
以薄圆环作为质量微元
r O
O
R
d m 2 r d r S
R
2
其中
S m/ R
4
2
R J z 2 r S d r r 2S 4 0
1 2 J z mR 2
1、质点的动量矩定理
d d dr d MO (m v ) ( r m v ) m v r (m v ) dt dt dt dt
dr d ( m v ) F ，且 O为定点， v 根据动量定理 dt dt

12动量矩定理

12动量矩定理

图12.7 钟摆
第12章 动量矩定理
12.1 转 动 惯 量
【例12.5】 匀质圆盘与匀质杆组成的钟摆如图12.7所示。已知圆盘质量m1， 直径d，杆的质量m2，长l，试求钟摆对悬挂轴O的转动惯量J0。
解：钟摆由匀质杆和匀质盘组成，所以有 = JO JO杆 + JO
其中
JO
=J c
+
m1
l
+
d 2
平方的乘积，即
12.7
J=z J zc + md 2
(12.7)
第12章 动量矩定理
12.1 转 动 惯 量
证明：如图12.5所示，设刚体总的质量为m，轴zc通过质心C，z与zc平行且 相距为d。不失一般性，可令y与yc重合，在刚体内任取一质量为mi的质点Mi,它 至zc轴和z轴的距离分别为ric和ri。刚体对于z、zc轴的转动惯量分别为
12.9
第12章 动量矩定理
12.1 转 动 惯 量
【例12.4】 质量为m，长为l的匀质杆如图12.6所示，求杆对yc的转动惯量。
解：由例12.1知
Jy
=
1 ml2 3
,根据平行轴定理式(12.7)有
J yc
=J y
−
md 2
=1 ml2 3
−
m
l
2
2
=1 12
ml 2
12.10
图12.6 匀质杆
在工程问题上，计算刚体的转动惯量时，常应用下面公式
12.3
第12章 动量矩定理
12.1 转 动 惯 量
Jz
=
mρ
2 z
(12.2)
ρ 其中m为整个刚体的质量， z 为刚体对z轴的回转半径，它具有长

第12章动量矩定理汇总

第12章动量矩定理汇总

第十二章动量矩定理§12—1质点和质点系的动量矩一、质点的动量矩质点Q的动量对于点0的矩，定义为质点对于点0的动量矩M O mv = r mvM z mv 二2 0Q AM O mv ［二M z mv动量矩的单位：kgm2/s、质点系的动量矩nL o 二為M o m i V ii』nL z八M z m i v iM O (mv)(r mv ) dtdtdr dtmv rmvdt绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的转动惯量与转动角 速度的乘积n n n2L z 八 M z mM八 m i y 订i =mmyy ynJ z 八 m"2id ：§12— 2动量矩定理、质点的动量矩定理M O mv =v mv r F dt-J—M O mv 二 M O F dt质点的动量矩定理：质点对某定点的动量矩对时间的一阶导数，等于作 用力对同一点的矩。

直角坐标投影式为d厂 一Mx(mv)= Mx(F ) dt pl 2 My(mv)=My(F ) dt plL 2M z (mv)= M z (F ) dtL z=J z ：特殊情形：当质点受有心力F的作用时，如图11-4所示，力矩M°(F)=O，则质点对固定点0的动量矩M o(mv)=恒矢量，质点的动量矩守恒。

例如行星绕着恒星转，受恒星的引力作用，引力对恒星的矩M°(F)=O，行星的动量矩M o (m v )=恒矢量，此恒矢量的方向是不变的，因此行星作平面曲线运动；此恒矢量的大小是不变的，即mvh=恒量，行星的速度v与恒星到速度矢量的距离h成反比。

(1)从而由式(1)得单摆运动微分方程为护阶0(2)解式(2) 得单摆的运动规律为9 =cp o Sin( 3n t +8)其中，3-g称为单摆的角频率，单摆的周期为例1如图所示单摆，由质量为m的小球和绳索构成。

单摆悬吊于点0,绳长摆在铅垂平面内绕点0作微振幅摆动，设摆与铅垂线的夹角为「为逆时针时正，如图所示。

第12章 动量矩定理

第12章 动量矩定理

2
r1
z1
α2
W
所以，重物上升 的加速度为
( M i12 mgR ) R a R 2 2 J1i12 J 2 mR 2
思考题
已知均质轮O1，半径R1，质量为m1; 均质 轮O2，半径R2，质量为m2，主动力矩M， 阻力矩Mf，求α1。
M
O2 O1
Mf
α2 Lo1 J 11 J 2 2
对于n个质点，有n个这样的方程，将这些方程求和，
则
n
内力系主矩 = 0
n n d M o (mi vi ) M o ( Fi (i ) ) M o ( Fi ( e ) ) dt i 1 i 1 i 1
所以得
n d n d n Mmi voi(mi v M o ( Fi ( e ) ) dt o ( M ) ii)1 (交换求导数与求和的次序) dt i 1 i 1
Lo ml l ml l 2ml 2
从本例可以知道，系统质心的速度虽然为零，系统对O 轴的动量矩并不等于零。 计算质点系的动量矩不能简单地 用质心的动量对某固定点或固定轴取矩。
例12-2
O ω
已知均质杆m，l，ω， 则杆的动量为
p = mvc = mωl/2
杆对O轴的动量矩为
质点A的动量对固定点O的矩：
z
F

A
B
Mo(mv)= r×mv
i x mv x j y mv y k z mv z
x A'
mv
MO(mv)
o
r
B' y
(mv)xy
大小= mv· sin =2S△OAB r 方位：过O且⊥△OAB；

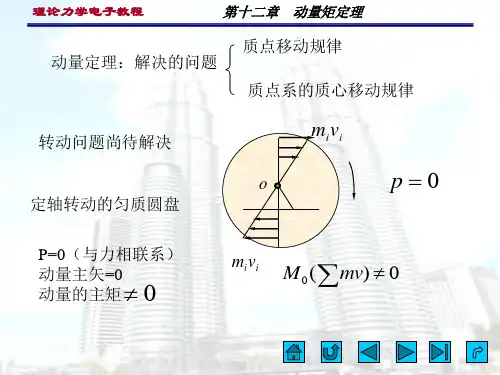
十二章动量矩定理


F mv
M0(F)
o
Ｑ
y
x
由牛顿第二定律
m
dv dt
F
d dt
(mv)
F
r
d dt
(mv)
r
F
d (r mv) r d(mv) dr mv
dt
ห้องสมุดไป่ตู้
dt dt
理论力学电子教程
第十二章 动量矩定理
d (r mv) r F dt
M0(mv) m0(F)
理论力学电子教程
第十二章 动量矩定理
C
m2
IOZ M
式中
M
m1
O
IOZ
1 3
m1L2
1 2
m2
r
2
m2L2
理论力学电子教程
第十二章 动量矩定理
代入已知值得：
IOZ
1 10 0.32 3
1 40 0.152 2
40 0.32
4.35kg m2
M 20 4.6rad / s2
IOZ 4.35
理论力学电子教程
第十二章 动量矩定理
dt
M y (mv)]
my (Fe )
d [
dt
M z (mv)]
mz (Fe )
理论力学电子教程
第十二章 动量矩定理
【典型题精解】
例12-1 滑块Ａ，Ｂ质量分别为２Ｋｇ，0.5Ｋｇ，用长１
米的绳连接，在水平光滑滑竿上滑动，绳和竿的质量不计。
竿绕铅垂轴转动，轴的摩擦也不计。当 rA 0.6m 时，滑块 Ａ以速度０.４ｍ／Ｓ沿竿向外运动，竿的角速度 0.5rad / s
求此时竿的角加速度。
1m
B rB

第12章-动量矩定理

它表达为刚体质量 m 与某一长度ρ z 旳平方
旳乘积： J z m z2
细直杆 均质圆环 均质圆板
J z /m 1 / 3 l2 z 0.5774 l
J z /m R2 z R
J z /m 1 / 2 R2 z 0.7071R
z 假如把刚体旳质量全部集中在与 轴相距为ρ z 旳点
上，则此质点对 z 轴旳转动惯量与原刚体相同。
四、平行轴定理
J z J z md 2
定理：刚体对任意轴旳转动惯量，等于刚体对 于经过质心、并与该轴平行旳轴旳转动惯量， 加上刚体旳质量与两轴间距离平方旳乘积。
z
O
z
d
ri
ri
C
O
mi
zi
y( y)
C点为质心；
O z 为质心轴，O z
为与之平行旳任
xi
一轴，距离为 d 。
x d x yi J z mi ri2 mi ( xi2 yi2 )
d dt
(
J
z
)
Jz
Mz
dω dt
(Fi
)M
M z (Fi )
z
(
FN
i
)
Fi
或
Jz
d2
dt2
M z (Fi )
或 J z M z (Fi )
FNi
与 m a Fi 比较
例：已知滑轮半径为 R ，转动惯量为 J ，带动滑轮
旳皮带拉力分别为 F1 和 F2 。求滑轮旳角加速度 。
F2 解：根据定轴转动微分方程
d(ri
mivi ) dt
ri
F (e) i
ri
Fi(i)
(i 1,2,, n)
相加得

动量矩定理

3 动量矩定理动量定理给出了三个独立的方程，在某种意义上来说，它只解决了一个点(质心)的运动问题，不足以全面地描述质点系的运动状态。

例如，一均质圆盘绕过质心且垂直于圆盘的定轴转动，不论圆盘转动快慢如何，也不论其转动快慢有何变化，它的动量始终为零。

这说明动量定理不能反映这种运动的规律。

动量矩定理反映了质点系外力系在空间的分布与质点系运动之间的规律。

设n 个质点组成质点系，其中第i 个质点的质量为m i ，矢径为r i ，瞬时速度为v i ，该质点对固定点O 的动量矩为L Oi (图8-1)定义为(8.1.12) ),...,2,1(,n i m i i i Oi =×=v r L 动量矩是一个矢量。

定义质点系对O 点的动量矩为质点系中每个质点对同一点动量矩的矢量和，即(8.1.13)i i ni i ni Oi O m v r L L ×==∑∑==11在直角坐标系中，质点系的动量矩可表示为(8.1.14) k j i L z y x O L L L ++=式中L x , L y , L z 为质点系动量矩L O 分别在轴x , y , z 上的投影。

类似静力学中力对点之矩和力对轴之矩的关系，有质点系对点O 的动量矩在通过该点的轴上的投影等于质点系对该轴的动量矩，即质点系对坐标轴x , y , z 的矩为(8.1.15)∑∑∑===−=−=−=ni ix i iy i i z n i n i iz i ix i i y iy i iz i i x v y v x m L v x v z m L v z v y m L 111)(,)(,)(作为特殊的质点系，刚体作平移和定轴转动时动量矩的计算相对简单。

(1) 平移刚体对O 点的动量矩 设平移刚体的质量为m ，同一瞬时刚体上各点的速度均相等，用v 表示，由式(8.1.13)得()v r v r v r L m m m C i i i i i O ×=×=×=∑∑)( (8.1.16)因此，刚体平移时，可将全部质量集中在质心，作为一个质点计算其动量矩。

材料力学

解： J 11 M 1 FtR1
R2 , M 1 , M 2求： 1. R1
J 2 2 Ft R2 M 2
1 i12 因 Ft Ft ， 2
M2 M1 R2 i12 ，得 1 J2 R1 J1 2 i12
§12-4 刚体对轴的转动惯量
J z mi ri 2
i 1 n
单位：kg·2 m
1.
简单形状物体的转动惯量计算
l l 3
3
(1)均质细直杆对一端的转动惯量
J z l x 2dx
0
l
由 m
l l ，得
1 2 J z ml 3
（2）均质薄圆环对中心轴的转动惯量
J z mi R 2 R 2 mi mR 2
（3）均质圆板对中心轴的转动惯量
(e) dLz M z ( Fi ) dt
内力不能改变质点系的动量矩.
例12-1 已知： R, J , M , , m ,小车不计摩擦.
求小车 R
( M Oe ) M mg sin R
d [ J mvR] M mg sin R dt
（2） 刚体绕定轴转动
Lz M z (mi vi ) mi vi ri
mi ri ri mi ri
转动惯量
2
J z mi ri 2 Lz J z
§12-2
1．质点的动量矩定理
设O为定点,有
动量矩定理
d d M O (mv ) (r mv ) dt dt dr d mv r (mv ) dt dt d 其中: (mv ) F d t dr v （O为定点） dt
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
因为系统外力对z轴的矩为零，
故系统对z轴动量矩守恒。
J10 = (J1 J2 )
2. 选轮2为研究对象
§12-3 刚体绕定轴转动的微分方程
主动力：F1, F2 , , Fn
约束力：FN1 , FN2
d dt
(
J
z)
M
z
(Fi
)
M
z
( FNi
)
M z (Fi )
即：J z
d
dt
M z (Fi )
或 J z M z (F ) 或
d2
Jz dt2 M z (F )
与 ma F 相似
例12-5
例12-1 续
解：1 、 LZ(OA)
Lz J z 用点的合成运动求ω
ve
va
sin
v 2
ve v
OC 4h
Lz (OA)
J z
JOv 4h
2、 LZ(板)
Lz mvrZ
Lz(板)
h 2
m1v
ve va
C
vr
例12-1 续
3、 LZ(E)
va v vr
Lz(E) hm2va hm2 (vr v)
d dt
Ly
(mv
)
M
y
(F)
d dt Lz (mv ) M z (F )
2. 质点系的动量矩定理
对第i个质点有：
d dt
LO (mivi )
M O (Fi(i) )
M O (Fi(e) )
对n个质点有：
d dt
LO
(mivi )
M O (Fi(i) )
M O (Fi(e) )
由于 M O (Fi(i) ) 0
LO m2vR JO
v R LO 10mr2
M (e) O
F
r
m2 gR
ksr 4mgr
d
dt
LO
=
n i 1
M
O
(
F (e) i
)
d
dt
,
a2
R
解得：
4mg ks a2 = 5m
3．动量矩守恒定律
若 MO (F (e) ) 0 ，则 LO 常矢量； 若 M z (F (e) ) 0 ，则 Lz 常量。
m(3R)2
3mR2
R
J zC 2
1 mR2 2
C2
根据平行轴定理
J z盘
J zC 2
m(R
l)2
1 2
mR2
16mR 2
33 2
mR2
Jz
J z杆
J z盘
39 mR2 2
§12-2 动量矩定理
1．质点的动量矩定理
设O为定点，有：
d dt
LO
(mv
)
d dt
(r
mv

)
dr
d
mv r (mv )
第 12 章 动 量 矩 定 理
本章重点：质点系动量矩的概念及计算，转动惯量 的概念，质点系相对于固定点的动量矩 定理，刚体绕定轴转动微分方程及其应 用。
§12-1 质点和刚体的动量矩 1．质点和质点系的动量矩(角动量)
质点Q对点O的动量矩的定义 LO (mv ) r mv
质点的动量对坐标轴的矩
d dt
LO
(mivi
)
d dt
LO
(mivi
)
d LO dt
得
dLO dt
M O (Fi(e) )
2. 质点系的动量矩定理
dLO dt
M O (Fi(e) )
称为质点系的动量矩定理：质点系对某定点O的动量
矩对时间的一阶导数，等于作用于质点系的外力对于
同一点之矩的矢量和。
投影式：
d Lx dt
2) 平行轴定理
J z J zC md 2
式中：zC轴为过质心且与z轴平行的轴，d 为z 轴与zC轴之间的距离。
即：刚体对于任一轴的转动惯量，等于刚体对通过质 心并与该轴平行的轴的转动惯量，加上刚体的质量与 两轴间距离平方的乘积。
例12-1
杆OA由铰链O与地面连接，它对轴O的转动惯量为JO；一高 为h、质量为m1的均质矩形板沿轴x以速度v平移，并推动杆OA 绕轴O转动；一质量为m2的质点E以相对速度vr在板上运动。试 求系统运动到图示位置时对轴O（轴z）的动量矩。
Lz Lz (mivi ) i 1
即 LO Lxi Ly j Lzk
2. 刚体的动量矩
(1) 刚体平移的动量矩 可将全部质量集中于质心，作为一个质点来计算。 LO rC mvC
2. 刚体的动量矩
(2)刚体绕定轴转动的动量矩
Lz Lz (mivi ) miviri
miriri miri2
转动惯量 J z miri2 单位：kg·m2
Lz J z
转动惯量是刚体转动时惯性的度量。质量是刚体移 动时惯性的度量。
3. 刚体对轴的转动惯量
转动惯量 J z miri2
教材P213表12－1列出了简单均质物体的转动惯量 1) 回转半径（惯性半径）的概念
z
Jz m
或
Jz
m
2 z
3. 刚体对轴的转动惯量
M x (Fi(e) )
d Ly dt
M y (Fi(e) )
d Lz dt
M z (Fi(e) )
注意：内力不能改变质点系的动量矩。
例12-3
已知：m1，r，k ，m2 ，R， JO 2mr 2 , R 2r, m1 m, m2 2m
求：弹簧被拉长s时，重物m2的加速度a2 。 解： 选系统为研究对象,受力分析如图 设塔轮该瞬时的角速度为ω，则
质点对z轴的动量矩 Lz (mv ) 是质点的动量在Oxy平
面的投影(mv)xy对O点的矩。
Lz (mv ) 是代数量，从 z 轴正向看，逆时针为正，顺时 针为负。
[LO (mv )]z Lz (mv )
单位：kg·m2/s
质点系的动量矩
对点的动量矩 对轴的动量矩
n
LO LO (mivi ) i 1 n
dt
dt
其中： d (mv ) F
dt
dr v (O为定点)
v mv 0
dt
d
dt LO (mv ) MO (F )
质点的动量矩定理
因此
d dt
LO
(mv
)
M
O
(F
)
称为质点的动量矩定理：质点对某定点的动量矩对
时间的一阶导数，等于作用力对同一点的矩。
投影式：
d dt
Lx
(mv
)
M
x
(F)
已知： R, J , F1, F2 ，求 。
解：
J (F1 F2 )R
(F1 F2 )R
J
由上式可见，只有当定滑轮匀速转动（包括静 止）或虽非匀速转动，但可忽略J 时， F1 、F2才相 等。
例12-6
已知： 0 , J1, J2 , t ，求：1.ω；2. Mf 解： 1. 选系统为研究对象
结果： Lz LOA L板 LE
JOu 4h
h 2
m1u
hm2 (vr
u)
例12-2
钟摆简化如图所示。已知均质细杆和均质圆盘的质量都为m，
圆盘半径R，杆长3R，求摆对通过悬挂点O并垂直于图面的z轴
的转动惯量。
O
解： J z J z杆 J z盘
C1
3R
查表得：
J z杆
1 ml 2 3
1 3