当前位置：文档之家 › 等比数列的概念完整PPT课件

等比数列的概念完整PPT课件

  • 格式：ppt
  • 大小：674.50 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

《等比数列的概念》课件

《等比数列的概念》课件

03
等比数列的应用
等比数列在数学中的应用
解题技巧
等比数列是数学中常见的数列类型， 它在解决数学问题时具有广泛的应用 。例如，在求解一些复杂数学问题时 ，可以利用等比数列的性质简化计算 过程。
公式推导
等比数列的通项公式和求和公式在数 学中经常被用来推导其他公式或解决 一些复杂的数学问题。这些公式是等 比数列应用的基石，能够提供解决问 题的有效途径。
等比数列的公比
总结词
表示等比数列中任意两项的比值
详细描述
等比数列的公比是任意两项的比值，通常用字母 q 表示。公比是等比数列中相 隔一项的两个数的比值，即 a_n/a_(n-1)。公比反映了等比数列中每一项与前一 项的比值。
等比数列的项数与项的关系
总结词
表示等比数列中项数与项的关系
详细描述
在等比数列中，任意一项的值可以用首项、公比和项数来表 示。例如，第 n 项的值可以用 a_n=a_1×q^(n-1) 来表示， 其中 a_1 是首项，q 是公比，n 是项数。这个公式揭示了等 比数列中项数与项的关系。
《等比数列的概念》ppt课件
目录 Contents
• 等比数列的定义 • 等比数列的性质 • 等比数列的应用 • 练习题与答案
01
等比数列的定义
等比数列的文字定义
总结词：简洁明了
详细描述：等比数列是一种特殊的数列，其中任意两个相邻项之间的比值都相等 。
等比数列的数学符号定义
总结词：专业严谨
详细描述：等比数列通常表示为 a_n，其中 a 是首项，r 是公比，n 是项数。其数学定义是 a_n = a * r^(n-1)，其中 r ≠ 0。
等比数列与等差数列的区别
总结词：对比分析

等比数列课件ppt

等比数列课件ppt

02
等比数列的通项公式
等比数列的通项公式推导
01
02
03
定义等比数列
等比数列是一个序列，其 中任意两个相邻项的比值 都相等。
推导通项公式
假设等比数列的首项为 $a_1$，公比为$r$，则第 $n$项$a_n$的通项公式 为$a_n = a_1 times r^{(n-1)}$。
证明通项公式
通过数学归纳法或迭代法 证明通项公式的正确性。
等比数列课件
• 等比数列的定义与性质 • 等比数列的通项公式 • 等比数列的求和公式 • 等比数列的应用 • 习题与解答
01
等比数列的定义与性质
等比数列的定义
总结词
等比数列是一种特殊的数列，其 中任意两个相邻项之间的比值都 相等。
详细描述
等比数列中，任意两个相邻项的 商是常数，这个常数被称为公比 。在等比数列中，每一项都是前 一项与公比的乘积。
举例说明
通过具体的例子来解释等比数列求和公式的推导过程。
等比数列求和公式的应用
解决实际问题
等比数列求和公式在解决实际问题中有着广泛的应用，如金融、工程、物理等 领域。
举例说明
通过具体的例子来展示等比数列求和公式的应用。
等比数列求和公式的变体
等差数列与等比数列的关系
01
等差数列和等比数列是两种不同的数列，但它们之间存在一定
01
第三组数列是等比数列，因为相 邻两项的比值都是1/2。
02
第四组数列也是等比数列，因为 相邻两项的比值都是1/2。
习题二：等比数列的通项公式
01
题目：已知等比数列的首项为 a，公比为q，求第n项的通项
公式。
02
答案与解析

等比数列的概念PPT优秀课件

等比数列的概念PPT优秀课件
(3) (4) (5) (6)
公比 q=2 递增数列 公比 q=3 递增数列
1 , x , x , x , x , ( x 0 )
234
公比 d= x
1 公比 q= 递减数列 2
1 1 1 1 , , , , 2 4 8 16
5，5，5，5，5，5，… 1，-1，1，-1，1，…
公比 q=1 非零常数列 公 比q= -1 摆动数列
为0.
等比数列、等差数列定义比较
等比数列：如果一个数列从第2项起，每一项与它 的前一项的比等于同一个常数（指与n无关的数）， 这个数列就叫做等比数列，这个常数叫做等比数 列的公比，公比通常用字母q表示。 等差数列：如果一个数列从第2项起,每一项与它的 前一项的差等于同一个常数，那么这个数列就叫 做等差数列.这个常数叫做等差数列的公差,公差通 常用字母d来表示.
讨论
已知等比数列 （1） 首项
a n
a1
： 能不能是零？
Why? 不能！！！
（2）公比q能不能是零？
Why? 不能！！！
等比中项
观察如下的两个数之间，插入一个什么数后者三个数就会成 为一个等比数列： （1）1，±3 ， 9 （3）-12， ±6 ，-3 （2）-1， ±2 ，-4 （4）1，±1 ，1
如果在a与b中间插入一个数G，使a，G，b成等比数列， 那么G叫做a与b的等比中项。
G ab G ab
2
等比中项与等差中项比较
G ab G ab
2
ab A 2
现给出等差中项的性质 1、在等差数列中，从第二项起,每 一项是相邻两项的等差中项。 2、在等差数列中，数列中的某一项 是与它“等距离”的两项的等差中 项。 你能类比中项的性质吗?可以用数学 式子表示吗?

等比数列的概念(课件)高二数学(人教A版2019选择性必修第二册)

等比数列的概念(课件)高二数学(人教A版2019选择性必修第二册)
4 = 3 = 1 2 = 1 3 ,
由此可得
……
= 1 −1 ≥ 2 .
又1 = 1 0 = 1 1−1 ，这就是说，当n=1时上式也成立.
首项为1 ，公比为q 的等比数列{ }的通项公式为
= 1 −1
过关测试
1.判断正误
1 1 1
B．a，a2，a3，…
C．s－1，(s－1)2，(s－1)3，…
D．0,0,0，…
2,
2
)
解析：A、C、D 不是等比数列，A 中不满足定义，C、D 中项可为 0，不符
合定义．
答案：B
3．2＋ 3和 2－ 3的等比中项是
A．1 B．－1
(
C．±1 D．2
答案：C
4．若数列x，x2，x3，x4，…为等比数列，则x应满足的条件是________．
（2）当 1 > 0, 0 < < 1或 1 < 0, > 1 时，等比数列{ }为递减数列；
（3）当ｑ＝１时，数列{ }为常数列；
（4）当ｑ＜０时，数列{ }为摆动数列.
典型例题
【典例1】 若等比数列{ }的第4项和第6项分别为48和12，求{ }的第5项.
分析：
(1)根据已知条件，建立关于a1，q的方程组，求出a1，q后再求an，这是常规方
法．
(2)充分利用各项之间的关系，直接求出q后，再求a1，最后求an，这种方法带有
一定的技巧性，能简化运算．
已知数列{an}是等比数列，公比q<1，且a2＝2，a1＋a2＋a3＝7.
(1)求{an}的通项公式．
(2)设bn＝log2an，求数列{bn}的前n项和．
数列①~⑥的公比依次是

等比数列的概念及基本运算ppt课件

等比数列的概念及基本运算ppt课件

篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
点评：(1)解决等比数列问题，关键是抓住首项 a1 和 公比 q，求解时，要注意方程思想的运用．
(2)运用等比数列求和公式时，要注意公比 q 是否为 1.当 n 较小时，直接利用前 n 项和的意义展开，不仅可避 开公比 q 的讨论，还可使求解过程简捷．
q3＝－2， 所以a1＝1，
或q3＝－12， a1＝－8.
所以 a1＋a10＝a1(1＋q9)＝－7.
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
a111－－qq10＝10， (2)(方法一)设公比为 q，则a111－－qq20＝30， 得 1＋q10＝3，所以 q10＝2. 所以 S30＝a111－－qq30＝a111－－qq10(1＋q10＋q20) ＝10(1＋2＋22)＝70. (方法二)因为 S10，S20－S10，S30－S20 仍成等比数列， 又 S10＝10，S20＝30， 所以 S30－30＝30－10102＝40，所以 S30＝70. 答案：(1)D (2)70
A．8
B．9
C．10
D．11
解：因为 a5a7＝a62，a7a9＝a82， 所以 a5a7＋2a6a8＋a7a9＝a62＋2a6a8＋a28＝(a6＋a8)2＝100.又 an＞ 0，所以 a6＋a8＝10.
答案：C
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
2．(2015·新课标卷Ⅱ)已知等比数列{an}满足 a1＝3，a1＋a3

高一数学《等比数列的定义》PPT课件

高一数学《等比数列的定义》PPT课件
等比数列
观察下面几个数列，看其有何 共同特点？
q=2 1 ， 2 ， 4 ， 8 ， 1 6 ， 2 2；
5 6 3
5，25，125，625，…； q=5 1 1 1 1 ， ，， ，； q=-1/2 2 4 8
共同特点：从第二项起，每一项与 前一项的比都等于同一个常数。
an1 1 等比数列的定义： q an
2 x 5 x 4 0 x 1 , 或 x 4 x 4 （舍） x 1
例 2 ：已知等比数列 { a ， { b 的项数相 n} n}
求证： { a b } 是等比数列。 n n
证明：设 a , b 首项分别为 a , q ; b , q n n 1 1 1 2
(与 n无关的数或式子）
问题1：等比数列中的项及公比能否为零 为什么？
a 0 ( n N ) , q 0 n

பைடு நூலகம்
判断下列数列是否是等比数列，如果是，请写出 它的公比。
2 , 2 , 2 , 2 , 3 , 3 , 3 , 3 0 , 2 , 0 , 2 0 , 0 , 0 , 0 a , a
a a q (a , q 0)
写出这几个等比数列的通项公式，首项，公 比 １，２，４，８，…263;
a 2 ( n 6 4 ) n
n 1
n 1
5，25，125，625，…;a 5 5 n
5
n
1 1 1 1 an ( ) 1 ， ，， ，； 2 2 4 8
(2)等比数列的通项公式: (3)等比中项目：
a a q ( aq , 0 ) n 1 1
2 a a a n n 1 n 1

等比数列课件.ppt经典实用

(5)a,a,a,a,a 不一定
非零常数列才是等比数列 是否存在既是等比数列又是等差数列的数列?
非零常数列
•等比数列课件.ppt
想一想 已知等比数列a1，a2，a3…an…, 公比为q，能否用a1，q和n表示an?
•等比数列课件.ppt
方法一 不完全归纳法
a2=a1q， a3=a2q=(a1q)q=a1q2，
•等比数列课件.ppt
对折报纸若干次所得 报纸的层数得到的数 列 2，4，8，16…
•等比数列课件.ppt
方法二 aa21=q aa32=q
累乘法
a4=a3q=(a1q2)q=a1q3， ……
…… a4
a3
=q
由此得到
×) aann-1=q
an=a1qn-1． a1与q均不为0．n=1时，仍 然成立。
an a1
=qn-1
an=a1qn-1
•等比数列课件.ppt
（1）an=a1qn-1 (2) an=amqn-m(n,m ∈N*）
•等比数列课件.ppt
由例1，例2
归纳：在等比数列中，知道其中任意两 项，则可以求任意指定的项。
•等比数列课件.ppt
数列 定义 公差（比）
等差数列 an - an-1 =d d 叫公差
等比数列
an q(n2)且nN* an1
q叫公比
定义变形
an=an-1+d
an=an-1 q
通项公式 一般形式
1,
1, 2
1 4
,
...,
1 2
n 1
, ...
1，2，22，23，…，263
这三个数列分别有什么特点？ 这三个数列有什么共同特点？
•等比数列课件.ppt

等比数列(53张PPT)


⇐把an＋1＝2an＋1变形为an＋1＋1＝2(an＋1)
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
[解]
(1)∵an＋1＝2an＋1，
∴an＋1＋1＝2(an＋1)． an＋1＋1 ∴ ＝2. an＋1 ∴{an＋1}是首项为a1＋1＝2，公比为2的等比数列． (2)由(1)知an＋1＝(a1＋1)qn－1＝2· 2n－1＝2n， ∴an＝2n－1.
Байду номын сангаас
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
[点评]
证明一个数列是等比数列的常用方法．
an＋1 an (1)定义法： a ＝q(常数)或 ＝q(常数)(n≥2)⇔{an} a n n －1 为等比数列． (2)等比中项法：a 等比数列． (3)通项法：an＝a1qn－1(其中a1，q为非零常数，n∈N＋) ⇔{an}为等比数列．
n－1 a q 通项公式是an＝ 1 .
3．等比中项 (1)如果三个数x，G，y组成 等比数列 ，则G叫做x和y的 等比中项．
2 G (2)如果G是x和y的等比中项，那么 ＝xy，即G＝± xy .
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
思考感悟
1．如何理解等比数列的定义？
∴数列{an}是等比数列．
人教A版· 数学· 必修5
进入导航
第二章 2.4 第1课时
系列丛书
[错因分析] 忽略了由Sn求an需n≥2，除此之外，还要 保证从第二项起每一项与它的前一项的比都等于同一非零 常数．
人教A版· 数学· 必修5
进入导航

等比数列定义及性质PPT课件

a1 首项为 a 1，公比为 q 的等比数 列的通项公式：
a n= a 1 q n－1 (a 1 ≠0 且 q ≠0
n ∈N +)
练习:写出下列等比数列通项公式
(1) 2，4，8，16，… a n =2n
(2) 2，2
2 , 4, 4
2…
n 1
a n= 2 2
(3)
1,
1 2
,Байду номын сангаас
1 4
,
1 8
,
…
.
1
一、温故知新：
1、等差数列定义： an－an－１=d(d为常数) 2、等差数列单调性：d>0单调递增
d<0单调递减 d=0常数列
3、 等 差 数 列 的： 通an项 a1公 (n式 1)d
用什么方法推出的呢？
.
2
观察以上数列各有什么特点：
1, 2, 4, 8, … (1) 1.对于数列(1),从第2项起,每一项 与前一项的比都等于___2_
an q(n 2) a n 1
或 a n 1 q ( n 1) an
（2)既是等比数列又是等差数列的数列存在吗？ 如果存在，你能举出例子吗？
非零的常数数列既是等差数列又是等比数列
.
5
探究： （1）等比数列的各项能等于0吗？为什么？
（2）公比q能等于0吗？
等差数列
由于等差数列是 作差 故a n , d 没 有要求
的前一项的差等于同 的前一项的 _比等于 _
一个常数,那么这个数 同一个常数，那么这个
列就叫做等差数列. 数列就叫做 等比数列
这个常数叫做等差数 这个常数叫做等 比 数
列的公差
列的 _公__比__

等比数列课件.ppt


③
-2, 2, -2, 2, ….
④
共同特点：从第二项起，每一项与前一项 的比都等于同一个常数．
讲授新课
1. 等比数列的定义: 一般地，若一个数列从第二项起，每一
项与它的前一项的比等于同一个常数，这个 数列就叫做等比数列.这个常数叫等比数列的 公比，用字母q (q≠0) 表示.
2.等比数列定义的符号语言:
等比数列的通项公式：叠乘法
a2 a3 a4 a5 ...... an an qn1
a1 a2 a3 a4
an1 a1
an a1q n1
等比数列注： （1）等比数列的首项不为0； （2）等比数列的每一项都不为0，即an 0 （3） q=1时，{an}为常数列；
湖南省长沙市一中卫星远程学校
不是 不是 是 a1=x0, q=x 不是
小结：判断一个数列是不是等比数列， 主要是由定义进行判断：
看 an1 是不是同一个常数？ an
注意：
(1) 等比数列｛an｝中, an≠0； (2)公比q一定是由后项比前项所得，而不
能用前项比后项来求，且q≠0； (3)若q＝1，则该数列为常数列．
(4)常数列 a, a , a , a , …
等比数列
问题情境:
情境一:折纸
如果能将一张厚度为0.05mm的报纸对折，
再对折，再对折‥‥‥依次对折50次，你相
信这时报纸的厚度可以在地球和月球之间 建一座桥？
对折 纸的
n
次数
对 折 一 次
对 折 二 次
对 折 三 次
对
对
折 四 次
…...
折
n
次
…...
纸的
2
层数
48
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(1) 1，3，9，27，…
1. 各项不能为零,即 a n 0
2. 公比不能为零,即 q 0
(2) 1, 1, 1, 1 , 3. 当q>0，各项与首项同号
2 4 8 16
(3) 5， 5， 5， 5，…
当q<0，各项符号正负相间
4. 数列 a, a , a , …
(4) 1，-1，1，-1，…
a 0 时,既是等差数列
(5) 1，0，1，0，…
又是等比数列;
(6) 0，0，0，0，…
a 0 时,只是等差数列
.
而不是等比数列.
等差数列通项公式的推导: an an1 d
方法一:(叠加法)
a2a1d
a3 a2 d a4…a3…d
(n-1)个 式子
an1an2 d
an an1 d
ana1(n1)d .
3
因此 a aq1638
2
1
32
16
答：这个数列的第1项与第2项分别是 与 8.
.
3
课堂互动
(1)一个等比数列的第5项是 4 ,公比是 1 ，求它的第1项；
9
3
解：设它的第一项是 a ，则由题意得 1
a1
( 1)51 3
4 9
解得， a1 3 6
答：它的第一项是36 .
（2）一个等比数列的第2项是10,第3项是20,求它的第1项与第4项.
解：设它的第一项是 a ，公比是 q ，则由题意得 1 a1q10 ， a1q2 20
解得， a1 5 ， q 2 因此 a4 a1q340 答：它的第一项是5.，第4项是40.
等比数列的例题
例2 已知 an,bn是项数相同的等比数列， 求证 an bn是等比数列.
证明:设数列an 首项为a 1,公比为q 1;b n 首项为b 1 ,公比为q 2 那么数列 an bn的第n项与第n+1项 分别为：
anam(nm)d
(n, m N* )
试问：在等比数列 a n 中，如果知道 a m 和公
比q，能否求 a n ？如果能，请写出表达式。
an amqnm (n,mN*)
.
等比中项的定义
如果在a与b中间插入一个数G，使a,G,b成 等比数列，那么G就叫做a与b的等比中项 在这个定义下，由等比数列的定义可得
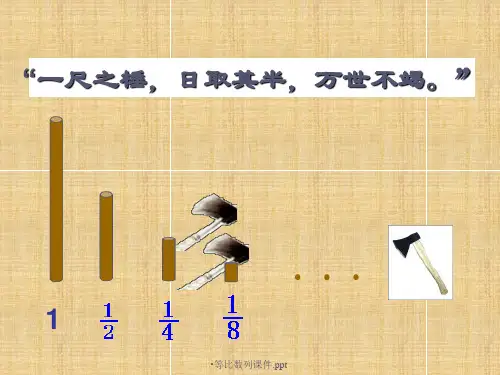
以上两个实例所包含的数学问题:
(1) 1 ，1
，1
，1
1
， ，…
2 4 8 16
(2) 1 ，2 ，4 ，8 ，16 ，32 ，… .
等比数列概念
等比数列
❖ 一般地，如果一个数列从第2项起，每一
项与它的前一项的 比 等于同一个常数， 那么这个数列就叫做等比数列 ，这个常数叫 做等比数列的公比（q）。
a 1 q 1 n 1 b 1 q 2 n 1 与 a 1 q 1 n b 1 q 2 n
即为 a 1 b 1(q 1q 2)n 1与 a 1 b 1(q 1q 2)n
an an 1b bn n1aa11 bb11((qq11 qq22))nn 1q1q2.它是一个与n无关的常数，
所以 an bn是一个以 q.1q2 为公比的等比数列
Gb 即 aG G 2 ab
G ab
.
等比数列的通项公式练习
课后练习P53 A1 ， 7
.
典型例题
例1 一个等比数列的第3项与第4项分别 是12与18,求它的第1项与第2项.
a 解：设这个等比数列的第1项是 ,公比是q ，那么 1 aq2 12 1
aq3 18 1
解得，
q3 2
16
，
a 1
aa38142或 8aa831428∵ 公比 q 为整数
aa83
4 128
q5 12832 q2 4
∴ a 10 = a 3×q 10 －3= －4×(. -2) 7= 512
回顾小结
等比数列
名称
等差数列
从第2项起,每一项与它前 概念 从第2项起,每一项与它前
一项的比等同一个常数
一项的差等同一个常数
公比(q)
常数
公差(d)
q可正可负,但不可为零 性质 d可正可负,且可以为零
an a1•qn1 通项 ana1(n1)d
(3) 5，5，5，5，5，5，…
是,公比 q= 1
2
是,公比 q=1
(4) 1，-1，1，-1，1，…
是,公 比q= -1
(5) 1，0，1，0，1，…
不是等比数列
(6) 0，0，0，0，0，…
不是等比数列
(7) 1,x,x2,x3,x4,L(x0)是,公比 q= x
.
对概念的更深理解
an1 q(是与 n无关的数,或 且q式 0） 子 an
合作交流
例3、等比数列 { a n } 中， a 4 ·a 7 = －512，a 3 + a 8 = 124, 公比 q 为整数，求 a 10. 法一：直接列方程组求 a 1、q。
法二：在法一中消去了 a 1，可令 t = q 5
法三：由 a 4 ·a 7 = a 3 ·a 8 = －512 a3 212 a34 512 0 a 312 或 a 8 3 4
方法二:(归纳法)
a2 a1d
a3 a2 d
(a1 d ) d
a12d
a4 a3d
(a1 2d ) d
…a1
3d
…
ana1(n1)d
an 等比数列通项公式的推导：an 1
q n2
方法一:叠乘法
方法二:归纳法
a2 q
a1
a3 q a2 a4 q
…a 3 …
(n-1)个 式子
an q
a n 1
a2 a1q
a3
aa12qq2(a1q)q
a4 a3q(a1q2)q
a1q3
……
an a1
qn1
.
an a1qn1
等比数列的通项公式
a 等比数列 a n ，首项为 1 ,公比为q,则通项公式为
an a1•qn1
当q=1时，这是 一个常函数。
an 0
.
变形结论:
在等差数列 a n 中
等差列
❖ 一般地，如果一个数列从第2项起，每一
项与它的前一项的 差 等于同一个常数， 那么这个数列就叫做等差数列 ，这个常数叫 做等差数列的公差（. d）。
课堂互动
观察并判断下列数列是否是等比数列:
(1) 1，3，9，27，81，…
是,公比 q=3
(2) 1, 1, 1, 1 ,
2 4 8 16
临沂一中高二数学组
.
旧知回顾
名称 概念
等差数列
从第2项起,每一项与它前
一项的差等同一个常数
常数
公差(d)
性质
d可正可负,且可以为零
通项
ana1(n1)d
通项 变形
anak(n(n,kk)Nd*)
.
创设情景,引入新课
（1）“一尺之棰，日取其半，万世不竭.”
（2） 一位数学家说过：你如果能将一张 纸对折38次，我就能顺着它在今天晚上爬 上月球。