新初一分班考试数学试题

一、选择题（每题5分，共25分）1. 下列数中，绝对值最小的是（）A. -3B. 3C. -2D. 22. 下列方程中，解为整数的是（）A. 2x + 1 = 7B. 3x - 2 = 5C. 4x + 3 = 8D. 5x - 4 = 93. 下列不等式中，不正确的是（）A. 2x + 3 > 7B. 3x - 4 < 5C. 4x + 5 ≤ 10D. 5x - 6 ≥ 74. 下列函数中，为一次函数的是（）A. y = 2x^2 + 3B. y = 3x + 4C. y = 4x^3 + 5D. y = 5x^2 + 65. 下列图形中，是平行四边形的是（）A. 矩形B. 正方形C. 三角形D. 梯形二、填空题（每题5分，共25分）6. 若 a > b，则 |a| 与 |b| 的关系是 ________。

7. 下列数中，负数的相反数是 ________。

8. 若 a = 3，b = -2，则 a + b 的值是 ________。

9. 下列函数中，y 与 x 成正比例的是 ________。

10. 下列图形中，对边平行的是 ________。

三、解答题（每题15分，共45分）11. 解方程：3x - 2 = 11。

12. 解不等式：4x + 5 > 20。

13. 已知函数 y = 2x - 3，求 x = 4 时的函数值。

14. 在等腰三角形 ABC 中，AB = AC，若 AB = 5，求 BC 的长度。

四、应用题（每题20分，共40分）15. 甲、乙两辆汽车同时从同一点出发相向而行，甲的速度为 60km/h，乙的速度为 80km/h。

两车相遇后，甲继续行驶 2h 到达目的地，乙继续行驶 3h 到达目的地。

求两地之间的距离。

16. 某商品原价为 200 元，打 8 折后，顾客再优惠 20 元。

求现价是多少元？。

初一新生分班考试数学试题含答案行4千米，他上山和下山用的时间相同，他上山用了（）小时。

A、1.5B、2C、2.5D、34、在一个三角形ABC中，角A的度数是60度，AB=5，AC=10，则BC=（）。

A、5B、5√3C、10D、10√35、如图，ABCD是一个正方形，E是BC的中点，F是CD的中点，则三角形AEF与正方形ABCD的面积比是（）。

A、1:2B、1:3C、1:4D、1:5初一新生编班考试数学试题考试时间：90分钟）一、你能快速又正确地填空吗？（1-7题每空0.5分，8-13题每题2分，共20分）1、用-9这十个数字组成最大的十位数是多少？把它改写成以万为单位的数是多少？四舍五入到亿位约为多少？2、3.04立方米等于多少立方米和多少立方分米？3、2÷（）= 10÷4 = 0.4 = 多少%？4、四位数21□5能被3整除，则□里可以填的数有哪些？5、___以八五折买了一件衬衫，比标价便宜18元，这件衬衫原来标价是多少元？6、两个数的最大公约数是12，最小公倍数是180，其中一个数是36，则另一个数是多少？7、甲、乙两数的和是48，如果把乙数的小数点向右移动两位后，甲、乙两数的比值为1，甲数是多少？8、如图，已知圆的直径是20厘米，大正方形的面积是多少平方厘米，小正方形的面积是多少平方厘米？9、把棱长为a厘米的两个正方体拼成一个长方体，长方体的表面积是原来两个正方体表面积的多少倍？10、一个边长20厘米的正方形内有一个最大的圆，这个圆的面积占正方形面积的多少%？11、父亲今年比儿子大30岁，3年后，父亲的年龄是儿子的4倍。

儿子今年多少岁？12、某人到十层大楼的第八层办事，不巧停电，电梯停升，如果从一层楼走到四层楼需要45秒，那么以同样的速度往上走到八层，还需要多少秒才能到？13、一个底面半径8厘米，高20厘米的圆柱形铁块，现在要把它锻造成一个底面与圆柱相同的圆锥，这个圆椎的高是多少厘米？二、相信你一定能选择正确。

一、选择题（每题2分，共20分）1. 下列数中，是偶数的是：A. 13B. 16C. 17D. 212. 小明有5个苹果，小红有3个苹果，他们两人一共有多少个苹果？A. 8B. 9C. 10D. 113. 下列分数中，分子大于分母的是：A. $\frac{2}{3}$B. $\frac{5}{4}$C. $\frac{1}{2}$D. $\frac{3}{3}$4. 如果一个长方形的长是8厘米，宽是4厘米，那么这个长方形的周长是多少厘米？A. 16B. 20C. 24D. 285. 下列图形中，不是平行四边形的是：A. 正方形B. 长方形C. 菱形D. 三角形6. 下列等式中，不成立的是：A. 3 + 5 = 8B. 6 - 2 = 4C. 7 × 2 = 14D. 8 ÷ 2 = 47. 小华今年12岁，他的爸爸比他大30岁，那么他的爸爸今年多少岁？A. 12B. 24C. 42D. 488. 一个班级有50名学生，其中男生占40%，那么这个班级有多少名女生？A. 20B. 30C. 40D. 509. 小明骑自行车去图书馆，速度是每小时15公里，他骑了2小时到达，那么他一共骑了多少公里？A. 10B. 15C. 20D. 3010. 一个长方体的长、宽、高分别是4厘米、3厘米、2厘米，那么这个长方体的体积是多少立方厘米？A. 24B. 36C. 48D. 60二、填空题（每题2分，共20分）11. 0.5的倒数是__________。

12. 下列各数中，质数有__________。

13. 下列各数中，奇数有__________。

14. 一个正方形的边长是6厘米，那么它的周长是__________厘米。

15. 一个三角形的高是4厘米，底边是6厘米，那么它的面积是__________平方厘米。

16. 下列图形中，长方形的长是8厘米，宽是4厘米，那么这个长方形的面积是__________平方厘米。

一、选择题（每题3分，共30分）1. 下列各数中，有理数是（）A. √-1B. πC. √4D. 2/3答案：C解析：有理数是可以表示为两个整数之比的数，即形如a/b（a、b为整数，b≠0）的数。

√4=2，是有理数。

2. 下列各数中，无理数是（）A. 2/3B. √9C. √2D. 1/π答案：C解析：无理数是不能表示为两个整数之比的数，如π、√2等。

√2是无理数。

3. 下列各数中，整数是（）A. -3/4B. 2/5C. √25D. 1/2答案：C解析：整数是没有小数部分的数，包括正整数、负整数和零。

√25=5，是整数。

4. 下列各数中，负数是（）A. 0B. -2C. 1/2D. √4答案：B解析：负数是小于零的数，-2是负数。

5. 下列各数中，正数是（）A. -3/4B. 0C. -2D. 1/2答案：D解析：正数是大于零的数，1/2是正数。

二、填空题（每题4分，共20分）6. （2）的平方根是_________。

答案：±√2解析：（2）的平方根是指一个数的平方等于2，即√2或-√2。

7. 下列方程的解为_________。

x - 5 = 2答案：x = 7解析：将方程两边同时加5，得x = 7。

8. 下列不等式的解集为_________。

2x + 3 < 7答案：x < 2解析：将不等式两边同时减去3，得2x < 4，再同时除以2，得x < 2。

9. 下列函数的图像为_________。

y = -2x + 1答案：直线解析：y = -2x + 1是一次函数，其图像为一条直线。

10. 下列图形的面积是_________。

长方形，长10cm，宽5cm答案：50cm²解析：长方形的面积公式为长×宽，所以面积为10cm×5cm=50cm²。

三、解答题（每题10分，共30分）11. （1）已知x² - 5x + 6 = 0，求x的值。

保密★启用前2023年小升初数学（新初一）普通校分班分层考试检测卷（一）考试分数：100分；考试时间：100分钟注意事项：1．答题前，填写好自己的姓名、班级、考号等信息，请写在答题卡规定的位置上。

2．选择题、判断题必须使用2B 铅笔填涂答案，非选择、判断题必须使用黑色墨迹签字笔或钢笔答题，请将答案填写在答题卡规定的位置上。

3.所有题目必须在答题卡上作答，在试卷上作答无效。

4.考试结束后将试卷和答题卡一并交回。

一、填空题。

（共26分）1．（本题3分）2022年5月10日是中国共产主义青年团成立100周年，全国共青团共有共青团员73715000名，横线上的数读作：( )，将这个数改写成用“万”作单位的数是( )，其中学生团员四千三百八十一万，横线上的数写作：( )。

2．（本题4分）朋朋向东走6m ，记作﹢6m ，那么他走了﹣50m 表示他向( )走了( )m ；如果朋朋从起点开始先向东走了10m ，再向( )走( )m ，这时他所在的位置记作﹣20m 。

3．（本题4分）320米＝( )千米 50分＝( )时38吨＝( )千克 0.5平方千米＝( )公顷 4．（本题2分）甲数比乙数多15，甲数是乙数的( )，乙数是甲、乙两数和的( )。

5．（本题2分）研究表明，眨眼有利于消除眼睛疲劳。

据统计，人在正常状态下每分钟眨眼25次。

看书时每分钟眨眼15次，玩电脑游戏时眨眼睛次数比正常状态时减少60%，看书时每分钟眨眼次数是正常状态的( )%，玩电脑游戏时每分钟眨眼( )次。

中国人群中近视眼的患病率非常高，而且近视人群有越来越年幼化趋势，我们应该注意用眼卫生。

6．（本题2分）小明今年10岁，哥哥比他大x 岁，哥哥今年( )岁。

10年后，哥哥比小明大( )岁。

7．（本题2分）李老师带51个同学到汾河公园去划船，共租了11条船，每条大船坐6人，每条小船坐4人，他们租了( )条大船，( )几条小船。

8．（本题1分）A 、B 两地相距400米，甲、乙、丙三人同时从A 地出发前往B 地，各自速度不变，当甲到B 地时，乙走了320米，丙走了240米，则当乙到B 地时，丙距B 地还有( )米9．（本题1分）一个直角三角形，其中两个锐角的度数比是2∶3，那么最小的一个角是( )°。

…○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：___________班级：___________考号：___________…………内…………○…………装…………○…………订…………○…………线…………○……………………○…………内…………○…………装…………○…………2024年小升初数学（新初一）名校分班分层考试检测卷考试分数：100分；考试时间：100分钟注意事项：1．答题前，填写好自己的姓名、班级、考号等信息，请写在答题卡规定的位置上。

2．选择题、判断题必须使用2B 铅笔填涂答案，非选择、判断题必须使用黑色墨迹签字笔或钢笔答题，请将答案填写在答题卡规定的位置上。

3.所有题目必须在答题卡上作答，在试卷上作答无效。

4.考试结束后将试卷和答题卡一并交回。

一、填空题。

（共39分）1．（本题6分）已知654565⨯=⨯=⨯a b c ，（a 、b 、c 均不为0）。

则a 、b 、c 相比较最大的是( )，最小的是( )。

【答案】 c a【分析】假设式子的值为1，利用求倒数的方法计算出a 、b 、c 的值，最后比较大小即可。

【详解】假设6541565a b c ⨯=⨯=⨯＝则56a ＝，65b ＝，54c ＝因为54＞65＞56，所以c ＞b ＞aa 、b 、c 相比较最大的是（ c ），最小的是（ a ）。

【点睛】掌握用求倒数比较大小的方法是解答题目的关键。

2．（本题3分）当x ＝( )时，1:3x 的比值恰好是13的倒数。

【答案】1【分析】由题意可知，13的倒数是3，1:3x ＝3，解方程求出未知数的值即可。

【详解】根据题意列出方程： 1:3x ＝3 解：13x ÷＝31133x ÷⨯＝3×13x ＝1所以，当x ＝（ 1 ）时，1:3x 的比值恰好是13的倒数。

【点睛】应用等式的性质2求出方程的解是解答题目的关键。

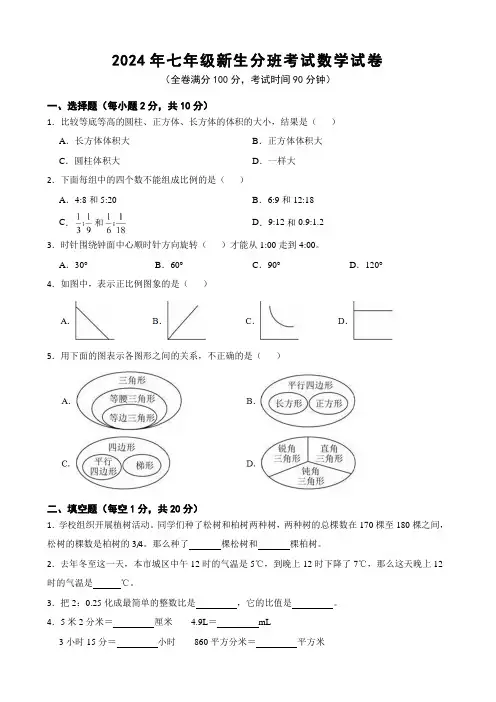
2024年七年级新生分班考试数学试卷（全卷满分100分，考试时间90分钟）一、选择题（每小题2分，共10分）1．比较等底等高的圆柱、正方体、长方体的体积的大小，结果是（）A．长方体体积大B．正方体体积大C．圆柱体积大D．一样大2．下面每组中的四个数不能组成比例的是（）A．4:8和5:20B．6:9和12:18C．和D．9:12和0.9:1.23．时针围绕钟面中心顺时针方向旋转（）才能从1:00走到4:00。

A．30°B．60°C．90°D．120°4．如图中，表示正比例图象的是（）5．用下面的图表示各图形之间的关系，不正确的是（）二、填空题（每空1分，共20分）1．学校组织开展植树活动。

同学们种了松树和柏树两种树，两种树的总棵数在170棵至180棵之间，松树的棵数是柏树的3/4。

那么种了棵松树和棵柏树。

2．去年冬至这一天，本市城区中午12时的气温是5℃，到晚上12时下降了7℃，那么这天晚上12时的气温是℃。

3．把2：0.25化成最简单的整数比是，它的比值是。

4．5米2分米＝厘米 4.9L＝mL3小时15分＝小时860平方分米＝平方米5．一只七星瓢虫的实际长度是5mm，画在图上后，量的长度是3cm，这幅图的比例尺是。

6．把如下图中的长方形以AD为轴旋转一周，得到一个圆柱体。

这个圆柱体的体积是cm3。

7．一个三角形的三个内角的度数比是2：5：2，这个三角形按角分是三角形；按边分是三角形。

8．一杯盐水重50克，它的含盐率为20%。

小青往这杯盐水中再倒入30克水，现在这一杯盐水的含盐率是。

9．根据算式的规律填空。

10．把一块长方体木料沿它的高锯掉2dm后，表面积减少72dm2，刚好成为一个正方体。

这个正方体的表面积是dm2，它的体积是dm3。

11．张爷爷家有121只鸽子，要保证至少有7只鸽子要飞进同一个鸽笼里，那么最多有个鸽笼。

12．劳动农场将一块长方形菜地分割成4个小长方形地对外出租（如图），其中小长方形地A、B、C 的面积分别是20m2、12m2、21m2，那么小长方形地D的面积是平方米。

2023~2024学年成都七中初中学校新初一入学分班考试数学试题（卷）（满分：100分时间：90分钟）一、选择题（将正确答案的番号填在括号里．每小题4分，共20分）1要使四位数104□能同时被3和4整除，□里应填（）．.A. 1B. 2C. 3D. 4【答案】D【解析】【分析】该题主要考查了数的整除，解答此题应结合题意，根据能被3和4整除的数的特征进行解答即可．根据能被4整除的数的特征：即后两位数能被4整除；能被3整除的数的特征：各个数位上数的和能被3整除，进行解答即可．+++=能被3整除，不【详解】解：A：后两位数是41，不能被4整除，各个数位上数的和是10416,6符合题意；+++=不能被3整除，不符合题意；B：后两位数是42，不能被4整除，各个数位上数的和是10427,7+++=不能被3整除，不符合题意；C：后两位数是43，不能被4整除，各个数位上数的和是10438,8+++=能被3整除，符合题意．D：后两位数是44，能被4整除，各个数位上数的和是10449,9故选：D．2. 用一只平底锅煎饼，每次只能放两只饼，煎熟一只饼需要2分钟（正反两面各需1分钟），那么煎熟3只饼至少需要_____分钟．（）A. 4B. 3C. 5D. 6【答案】B【解析】【分析】本题考查了推理与论证，在解答此类题目时要根据实际情况进行推论，既要节省时间又不能造成浪费．若先把两只饼煎熟，则在煎第三张饼时，锅中只有一只饼而造成浪费，所以应把两只饼的两面错开煎，进而求解即可．【详解】∵若先把两只饼煎至熟，势必在煎第三只饼时，锅中只有一只饼而造成浪费，∴应先往锅中放入两只饼，先煎熟一面后拿出一只，再放入另一只，当再煎熟一面时把熟的一只拿出来，再放入早拿出的那只，使两只饼同时熟， ∴煎熟3只饼至少需要3分钟． 故选：B ．3. 投掷3次硬币，有2次正面朝上，1次反面朝上，那么第4次投掷硬币正面朝上的可能性是（ ） A.12B.14C.13D.23【答案】A 【解析】【分析】本题主要考查可能性的大小，熟练根据概率的知识得出可能性的大小是解题的关键．根据每次投掷硬币正面朝上的可能性都一样得出结论即可． 【详解】解：每次投掷硬币正面朝上的可能性都为12． 故选：A ．4. 一串珠子按照8个红色2个黑色依次串成一圈共40粒．一只蟋蟀从第二个黑珠子开始其跳，每次跳过6个珠子落在下一个珠子上，这只蟋蟀至少要（ ）次，才能又落在黑珠子上． A. 7 B. 8 C. 9 D. 10【答案】A 【解析】【分析】本题关键是理解这只蟋蟀跳跃的规律，难点是得出跳过的珠子数与循环周期之间的关系． 这是一个周期性的问题，蟋蟀每次跳过6粒珠子，则隔7个珠子，把珠子编上号码，将第2粒黑珠记为0，以后依次将珠子记为1,2,3,39…．其中0,9,10,19,20,29,30,39的8颗珠子是黑色；蚱蜢跳过的珠子号码依次是0,7,14,21,28,35，42,49…，因为周期是40，再根据周期性的知识解决即可． 【详解】解：观察可知，每次跳过6粒珠子，则隔7个珠子，将第2粒黑珠记为0，以后依次将珠子记为1,2,3,39…．其中0,9,10，19,20,29,30,39的8颗珠子是黑色．蚱蜢跳过的珠子号码依次是0,7,14,21,28,35,42,49…，即7的倍数； 周期应是40,4940−9=，就相当于一圈后落在“9”号黑珠子上； 即这只蟋蟀至少要7次，才能又落在黑珠子上；故选：A．5. 仓库里的水泥要全部运走，第一次运走了全部的12，第二次运走了余下的13，第三次运走了第二次余下的14，第四次运走了第三次余下的15，第五次运走了最后剩下的19吨．这个仓库原来共有水泥_____吨．（）A. 78B. 56C. 95D. 135【答案】C【解析】【分析】本题考查分数除法的应用，此题应从后向前推算，分别求出第三，二，一次运过之后，还剩下的数量，即可求解．【详解】∵第五次只剩下19吨，∴第三次运过之后，还剩下195 19154÷−=吨，那么第二次运过之后，还剩下951951443÷−=吨，那么第一次运过之后，还剩951951332÷−=吨那么没经过运输之前，仓库中有9519522÷=吨，故选：C ．二、填空题（每小题3分，共30分）6.132吨=（）吨（）千克．70分=（）小时．【答案】①. 3 ②. 500 ③. 7 6【解析】【分析】根据1吨=1000千克、1小时=60分计算即可．【详解】解：∵11000=5002×千克，∴132吨=（3）吨（500）千克．∵70÷60=76小时，∴70分=（76）小时． 故答案为：3，500；76．【点睛】本题考查了单位换算，熟练掌握1吨=1000千克、1小时=60分是解答本题的关键． 7. 把0.45:0.9化成最简整数比是_____∶_____；11:812的比值是_____． 【答案】 ①. 1 ②. 2 ③. 1.5 【解析】【分析】此题主要考查了化简比和求比值的方法，另外还要注意化简比的结果是一个比，它的前项和后项都是整数，并且是互质数；而求比值的结果是一个商，可以是整数、小数或分数．用比的前项除以后项即可．详解】解：0.45:0.91:2=，11111:12 1.58128128=÷=×= 故答案为∶1，2，1.5． 8. 111112123123100+++++++++++ ． 【答案】200101【解析】【分析】先确定，分数的变化规律，后整理计算即可． 【详解】∵12112()123n (1)1n n n n ==−++++++ ，∴111112123123100+++++++++++ =1111112()1223100101−+−++−=12(1)101−=200101． 【点睛】本题考查了分数中的规律问题，熟练掌握拆项法找规律计算是解题的关键． 9. 定义运算：35a b a ab kb =++ ，其中a 、b 为任意两个数， k 为常数．比如：27325277k =×+××+ ，若5273= ，则85= _____．【答案】244 【解析】【分析】此题考查了有理数的四则混合运算和解一元一次方程，根据5273= 得到方程，解方程得到4k =，【再计算85 即可．【详解】解：由5235552273k =×+××+= ， 解得4k =，∴853*********=×+××+×= ， 故答案为：24410. 某年的10月份有四个星期四、五个星期三，这年的10月8日是星期_____． 【答案】一 【解析】【分析】本题主要考查数字规律，有理数混合运算，根据题意，找出循环规律，是解题的关键． 【详解】解：10月有31天，四个星期四，五个星期三，∴31号是星期三，31823−=（天），2373÷=（周） 2（天），把星期三往前推2天，是星期一， ∴10月8号是星期一， 故答案为：一．11. 某小学举行数学、语文、科学三科竞赛，学生中至少参加一科的：数学203人，语文179人， 科学165人，参加两科的：数学、语文143人， 数学、科学116人，语文、科学97人．三科都参加的：89人，这个小学参加竞赛的总人数为_____人． 【答案】280 【解析】【分析】根据题意，至少参加一科的：数学203人，语文179人，常识165人．参加两科的：数学，语文143人，数学、常识116人，语文、常识97人，三科都参加的有89人．根据容斥问题，参加三科的人数为：(20317916514311697)++−−−人，由于三科都参加的有89人，所以这个小学参加竞赛的总人数为：(2031791651431169789)++−−−+．据此解答．本题考查了容斥问题的灵活运用，关键是明确它们之间的包含关系．【详解】解：2031791651431169789280++−−−+=（人） 答：这个小学参加竞赛的总人数有280人． 故答案为：280．12. 一个长方体的长、宽、高之比为3:2:1，若长方体的棱长总和等于正方体的棱长总和，则长方体的表面积与正方体的表面积之比为_____，长方体的体积与正方体的体积之比为_____． 【答案】 ①. 11:12 ②. 3:4【解析】【分析】此题主要考查了长方体和正方体的棱长总和、表面积、体积的计算，直接把数据代入公式解答即可．设长方体的长宽高分别为3a 、2a 和a ，则其棱长之和为()43224a a a a ×++=，从而正方体棱长为24122a a ÷=．根据长方体和正方体的表面积公式计算求得长方体表面积与正方体的表面积比；根据长方体和正方体的体积公式计算求得长方体体积与正方体的体积之比【详解】设长方体的长、宽、高分别为3a 、2a 和a ，则其棱长之和为()43224a a a a ×++=，从而正方体棱长为24122a a ÷=．长方体表面积为()22323222a a a a a a a ××+×+×=， 正方体表面积为()226224a a ×=，其比为2222:2411:12a a =．长方体体积为 3326a a a a ××=，正方体体积为()3328a a =，其比为336:83:4a a =． 故答案为：11:12； 3:4．13. 甲、乙两地相距300千米，客车和货车同时从两地相向开出，行驶2小时后，余下的路程与已行的路程之比是3：2，两车还需要经过_____小时才能相遇． 【答案】3 【解析】由于客车和货车的速度和一定，行驶的时间和路程成正比例，所以根据“余下的路程与已行的路程之比是3：2”可得：余下的路程需要的时间与已行的时间之比也是3：2，据此求解即可． 【详解】由题意得：2233÷=(小时) 故答案：3．14. 如图，长方形ABCD 中，12AB =厘米，8BC =厘米，平行四边形BCEF 的一边BF 交CD 于G ，若梯形CEFG 的面积为64平方厘米，则DG 长为_____．【答案】4厘米 【解析】为【分析】本题考查了梯形的面积公式，一元一次方程的实际运用，解题的关键是设未知数，找准等量关系，建立方程求解．根据图形可得=64ABGD CEFG S S =梯形梯形，设DG 的长度为x 厘米， 则有()1128642x +××=，解出方程即可． 【详解】解：由图可知：长方形ABCD 和平行四边形BCEF 底边和高相同，故它们面积相同，GCB ABCD ABGD S S S =− 矩形梯形，64BCEF GCB CEFG S S S =−= 梯形平方厘米，， =64ABGD CEFG S S ∴=梯形梯形，设DG 的长度为x 厘米， 则()1128642x +××= ()128642x +××896128x +=832x =4x =，即DG 长为4 厘米， 故答案为：4厘米．15. 自然数按一定的规律排列如下：从排列规律可知，99排第_____行第_____列． 【答案】 ①. 2 ②. 10 【解析】【分析】本题考查了规律问题的探究．通过观察知第1行中的每列中的数依次是1、2、3、4、5…的平方；在第2行中的每列中的数从第2列开始依次比相应的第1行每列中的数少1；据此规律第1行中的10列的数是10的平方，第2行中的10列的数是100199−=．【详解】解：由图表可得规律：每列的第1个数就是列的平方； 10的平方是100，99在100的下方， 所以99排在第2行第10列， 故答案为：2；10．三、计算题（能用简便方法计算的请用简便方法计算．共20分）16. （1） 计算：2255977979 +÷+ ；（2） 计算：121513563+++×； （3） 计算：47911131531220304256−+−+−； （4） 计算：11111155991313171721++++×××××． 【答案】（1）13；（2）136；（3）78；（4）521【解析】（1）将229779 + 变形为551379+，可进行简便运算；（2）利用乘法分配律，将原式变形为11525136353++×+×进行简便运算； （3）利用裂项相消法进行简便运算； （4）利用裂项相消法进行简便运算； 【详解】解 ：（1）2255977979 +÷+6565557979+÷+5555137979=+÷+13=；（2）121513563+++× 11525136353=++×+× 35252353=×+× 5223=+ 136=；（3）47911131531220304256−+−+− 4111111111133445566778 =−+++−+++−+4111111111133445566778=−−++−−++−− 118=-78=； (4)11111155991313171721++++××××× 11111111111455991313171721 =×−+−+−+−+−111421 =×−120421=× 521=． 四、解答题（请写出必要的解题过程．每小题6分，共30分）17. 如图所示是两个正方形，大正方形边长为8，小正方形边长为4，求图中阴影部分的面积．（单位：厘米，π取3.14）【答案】20.56平方厘米 【解析】【分析】本题考查计算不规则图形的面积，BEF △的面积减去小正方形与扇形GAF 面积之差，即可求出阴影部分的面积． 【详解】解：()21184444π424 ×+×−×−××24164π=−+ 84 3.14=+×20.56=(平方厘米)答：阴影部分面积为20.56平方厘米．18. 学校计划用一批资金购置一批电脑，按原价可购置60台，现在这种电脑打折优惠，现价只是原价的75%，用这批资金现在可购买这种电脑多少台？【答案】用这批资金现在可购买这种电脑80台． 【解析】1，用1乘上60台，就是总钱数，然后用1乘上75%求出现在的单价，再用总钱数除以现在的单价即可． 【详解】设原来每台的单价是1(160)(175%)80×÷×=台答：用这批资金现在可购买这种电脑80台19. 在甲、乙、丙三缸酒精溶液中，纯酒精的含量分别占48%、62.5%和23．已知三缸酒精溶液总量是100千克，其中甲缸酒精溶液的量等于乙，丙两缸酒精溶液的总量．三缸溶液混合后，所含纯酒精的百分数将达56%．那么，丙缸中纯酒精的量是多少千克？【答案】丙缸中纯酒精的量是12千克 【解析】【分析】本题考查了百分数的应用，一元一次方程的应用；根据题意易得甲缸酒精溶液的量=乙缸酒精溶液的量+丙缸酒精溶液的量50=千克，从而可设丙缸中酒精溶液的量是x 千克，则乙缸中酒精溶液的量是()50x −千克，然后根据题意可得：()25048%62.5%5010056%3x x ×+−+×，最后进行计算即可解答． 【详解】解： 三缸酒精溶液总量是100千克，其中甲缸酒精溶液的量等于乙，丙两缸酒精溶液的总量，∴甲缸酒精溶液的量=乙缸酒精溶液的量+丙缸酒精溶液的量1100502=×=(千克)， 设丙缸中酒精溶液的量是x 千克，则乙缸中酒精溶液的量是()50x −千克，由题意得：()25048%62.5%5010056%3x x ×+−+×， 解得：18x =， ∴丙缸中纯酒精量218123=×=(千克)， ∴丙缸中纯酒精的量是12千克． 20. 一家工厂里2个男工和4个女工一天可加工全部零件的310，8个男工和10个女工一天内可加工完全部零件．如果把单独让男工加工和单独让女工加工进行比较，要在一天内完成任务，女工要比男工多多少人？【答案】女工要比男工多18人．【解析】【分析】本题主要考查了二元一次方程组的应用——工程问题．解题的关键是熟练掌握工作量与工作效率和工作时间关系，列方程计算．设男工的工作效率为x ，女工的工作效率为y ，根据2个男工和4个女工一天可加工全部零件的310，8个男工和10个女工一天内可加工完全部零件，列出方程组，解方程组即可．【详解】设男工的工作效率为x ，女工的工作效率为y ， 根据题意得，324108101x y x y += +=， 解得，112130x y = =， 如果单独让男工加工或单独让女工加工， 需要女工113030÷=（人）， 需要男工111212÷=（人）， 女工比男工多181230=−（人）． 的故女工比男工要多18人．21. 如图，有一条三角形的环路，A 至B 段是上坡路，B 至C 段是下坡路，A 至C 段是平路，A 至B 、B 至C 、C 至A 三段距离的比是345：：，小琼和小芳同时从A 出发，小琼按顺时针方向行走，小芳按逆时针方向行走，2个半小时后在BC 上的D 点相遇，已知两人上坡速度是4千米/小时，下坡速度是6千米/小时，在平路上的速度是5千米/小时．问C 至D 段是多少千米？【答案】2千米【解析】【分析】本题主要考查了二元一次方程组的实际应用，设3km 4km 5km km AB a BC a AC a CD x ====，，，，根据时间=路程÷速度，结合2个半小时后在BC 上的D 点相遇，列出方程组求解即可．【详解】解：设3km 4km 5km km AB a BC a AC a CD x ====，，，， 由题意得，34 2.5465 2.554a a x a x − += += 解得2x a ==，答：CD 的实际距离为2千米。