混联电路之等效电路

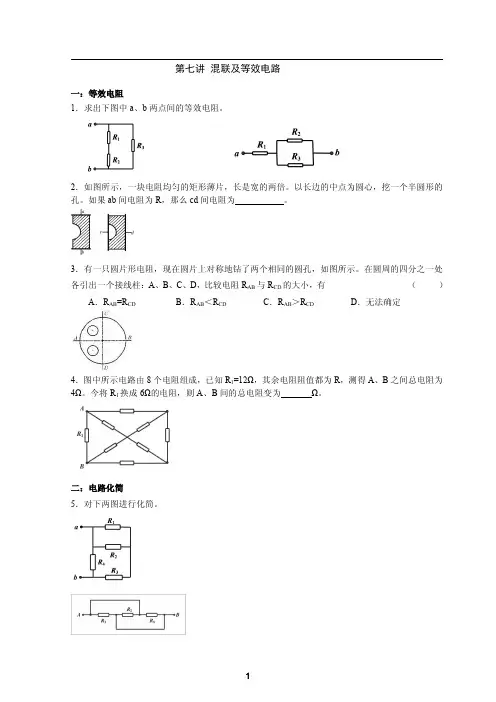
一：等效电阻1．求出下图中a 、b两点间的等效电阻。

2．如图所示，一块电阻均匀的矩形薄片，长是宽的两倍。

以长边的中点为圆心，挖一个半圆形的孔。

如果ab 间电阻为R ，那么cd 间电阻为。

3．有一只圆片形电阻，现在圆片上对称地钻了两个相同的圆孔，如图所示。

在圆周的四分之一处各引出一个接线柱：A 、B 、C 、D ，比较电阻R AB 与R CD 的大小，有（）A ．R AB =R CD B ．R AB ＜R CDC ．R AB ＞R CD D．无法确定4．图中所示电路由8个电阻组成，已知R 1=12Ω，其余电阻阻值都为R ，测得A 、B 之间总电阻为4Ω。

今将R 1换成6Ω的电阻，则A 、B 间的总电阻变为Ω。

二：电路化简5．对下两图进行化简。

第七讲混联及等效电路6．如图所示的电路，若R1:R2:R3:R4=1:2:3:4，则每个电阻两端的电压之比为。

附加7．如图所示，R1=R3=4Ω，R2=R5=1Ω，R4=R6=R7=2Ω，求AB两点间的电阻。

8．图中R1=3欧，R2=4欧，R3=6欧，U ab=6伏，则电流表A1、A2的读数分别是（）A．2.5安，3.5安B．3.5安，2.5安C．0安，0安D．5.5安，5.5安9．如图所示，已知R2=R4，R5=5欧，安培表A1、A2示数分别为3安和7安。

若A、B间的电压一定，且安培表的电阻不计，则R5两端的电压为伏。

三：电表内阻10．按图所示用伏安法测量电阻，如果考虑到电压表，电流表本身都有一定的电阻，那末测量值和实际值的关系应该是（）A．测量值比实际值大B．测量值比实际值小C．测量值等于实际值D．以上情形都有可能附加11．用一个伏特表直接测量某一电源的电压时，读数为6V。

若给这个伏特表串联一个200Ω的电阻后，再去测量同一电源的电压，其读数为5V。

则这个伏特表本身的电阻是Ω。

混联电路的动态与故障分析一：动态电路1．如图所示，当滑动变阻器的金属滑片P向右移动时，安培表A的示数将，伏特表V1的示数将，伏特表V2的示数将。

《电工基础》混联电路等效变换的教学简析内容摘要：通过对混联电路的等效变换概念的构建、作用的理解、条件和方法的掌握等教学过程的简析，阐述了电路的等效变换法在分析计算混联电路的授课技巧。

关键词：混联电路 等效变换 简析在《电工基础》课程的混联电路的分析与计算中，具有电路连接复杂、变换灵活和电路计算繁琐的特点，而电路等效变换是分析、计算复杂电路的有效而简便的方法，通过电路分析题的训练，可以增强学生分析问题的灵活性和技巧，培养分析问题的思维品质。

而在电路分析中，如何对电路进行合理的等效变换却总是困扰学生的一个难点问题。

为了使学生能够正确应用等效变换的方法分析求解、分析混联电路，提高学生的分析问题和解决问题的能力，笔者通过教学经验，对其教学方法进行简析如下：一、构建概念是讲解电路等效变换的前提要使学生正确理解电路的等效变换，必须正确地构建等效变换的概念。

明确等效就是在一定的条件下，两种不同的事物在某些方面具有相同的效果。

例如电压源与电流源的等效变换是指两个电路的外特性，即两个电路对应端的电流、电压关系完全相同。

具体而言，如果在两个电路端的对应端分别施加相同的电流源，则两个电路各自对应端间的电压应该相等。

反之，若在两个电路端的对应端分别施加相同的电压源，则两个电路各自对应端流入（或流出）的电流应该相等。

至于两个电路的内部结构可以完全不同。

如图（1）所示的电压源和电流源，它们是两个内部结构完全不同的电路，若它们两端分别向同一个负载R L 供电时，都能提供相同的U 、I 和功率，对于负载R L 来讲，无论是哪一种电源供电结果是一样的，我们就说这两个电路就是为等效电路。

当然要强调一点是指外电路的作用等效，即电源所起的作用相同。

理解了电路等效的含义之后，就可以构建电路等效变换的概念。

电路等效变换是指电路的一部分变换成另一种结构形式而能保持任意未改变部分各处电压电流不变。

如图（1）所示，则电流源可以替代电压源为负载R L 供电；当然，电压源也可以替代电流源为负载R L 供电。

混联电路分析复习
一．完整等效电路的画法
1.先把电源画出来，电源可包含内阻或者包含和电源串联的电阻；
2.再从电源两端开始画负载电阻。

(1)利用电流的流向及电流的分、合，画出等效电路图；
(2)利用电路中各等电位点画出等效电路。

(3)技巧
①看电路的结构特点：首尾相连就是串联，首首尾尾相连就是并联。

②看电压、电流关系：电流相同就是串联，电压相同就是并联。

③对电路作变形等效：扭动变形；短路线任意压缩和伸长；沿着导线移动。

二．分析方法一（由总到分的思路）
三．分析方法二（由分到总的思路）。

混联电路等效电阻计算的有效方法作者：黄宁李素云来源：《课程教育研究·上》2016年第01期【摘要】电工学教材中对于复杂混联电路的等效电阻计算介绍不多，导致学生求解时十分困难，甚至出现无从下笔，针对这种情况，总结教学经验，归纳出几种较直观和容易理解与掌握的求解方法，介绍各种方法的计算步骤，并指出这些方法的各自特点和相应的适用场合，上述几种方法有助于学生快速提高解题能力，可进一步提高教学效果。

【关键词】混联电路等效电阻末端递推法描点法【Abstract】 There is little introduction for calculating the equivalent resistance of hybrid circuit in electrotechnics textbook， which causes to difficultly solve and did not know where to start. In view of this situation， the teaching experience was summarized， several more intuitive and easily grasped methods were summed up， calculative steps of these methods were introduced， and respective characteristics and corresponding application of these methods were pointed out. Above several methods can help students quickly increase ability of solving problems， and further improve the teaching effect.【Key words】hybrid circuit； equivalent resistance； terminal recurrence method； depicting points method【基金项目】广西高等教育教学改革工程项目（2013JGA243）。

电容电感串等效方式
在电容电感串中，等效的方式是：电容和电感之间相互转化，最终达到一个动态平衡的状态。

首先，在没有电阻的电感、电容混联电路中，在确定的工作频率下，等效的结果只有三种情况：
1.阻抗为容性。

2.阻抗为感性。

3.谐振状态（阻抗为零或无穷大）。

其次，在电路端口依据电路的连接关系，写出其复阻抗表达式并将其整理成最简形式，若给定频率和元件参数，依据表达式可以直接判别等效结果是容性还是感性，或是谐振。

最后，在实际等效中，最终电阻等效为C//（R+L）。

电容等效为连接电阻Rs串联（一个电容C并联一个绝缘体电阻Rd）。

混联电路等效电阻的计算混合联接电路是指由串联和并联组成的复杂电路。

在这样的电路中，电流和电压的分布相对复杂，因此需要计算等效电阻来简化电路分析。

计算混合电路的等效电阻需要考虑两种情况：串联情况和并联情况。

下面将分别介绍这两种情况的计算方法。

1.串联情况：在串联电路中，电流只能沿着一条路径流动，因此等效电阻等于电路中各个电阻之和。

例如，如果电路中有3个串联电阻R1、R2和R3，那么等效电阻R等于R1+R2+R3一般来说，如果电路中有n个串联电阻，则等效电阻R等于电路中所有电阻的和，即R=R1+R2+...+Rn。

2.并联情况：在并联电路中，电流可以拆分为多个分支，每个分支通过一个电阻。

等效电阻是并联电阻的倒数之和的倒数。

例如，如果电路中有3个并联电阻R1、R2和R3，那么等效电阻R等于(1/R1+1/R2+1/R3)^(-1)。

一般来说，如果电路中有n个并联电阻，则等效电阻R等于(1/R1+1/R2+...+1/Rn)^(-1)。

当混合电路中既有串联又有并联电阻时，可以按照以下步骤计算等效电阻：步骤1：将电路中的并联电阻用等效电阻替代，这样就可以将电路简化为一个等效串联电路。

步骤2：计算串联电路的等效电阻。

步骤3：将步骤2中计算得到的等效电阻替代原来的并联电阻，这样就可以得到整个混合电路的等效电阻。

需要注意的是，计算混合电路的等效电阻可能会涉及到一些电路定理和公式，例如欧姆定律、基尔霍夫定律等。

在具体计算时还需要考虑电路的性质，如温度、功率、电流方向等。

总结起来，计算混合电路的等效电阻需要先计算串联部分的等效电阻，再计算并联部分的等效电阻，最后将它们组合在一起得到整个电路的等效电阻。

通过这样的计算，可以简化电路的分析和计算。

混联电路的分析方法一、方法概述1．问题初体验如何对图1所示的电路进行简化，并指出各电表测量的对象。

分析 电路中接入了一只电流表和一只电压表，在一般情况下，电压表的内阻是较大的，其分流作用很小，而电流表的内阻可认为是零。

其等效电路图如图2所示，其中R 2、R 3可认为无电流通过。

因此， 测量的是流过R 1的电流，测量的是R 1两端的电压.2．串并联电路的特点和规律 表面上看复杂的电路，最终都可简化为串、并联或两者混联的方式。

所以熟练掌握串、并联电路的特点和规律，是识别和简化电路的基本出发点。

特别要明确这几个特点：（1）串联电路中，电流处处相等，从电势上看，沿电流方向每经过一个电阻电势要降低；（2）并联电路中，总电流等于各支路电流之和，从电势上看，各支路两端电势分别相等；（3）导线理想化，即认为是“有电流、无电阻”，所以导线上各点是等势点。

3．电路简化的等效处理原则（1）无电流的支路除去；（2）电势相等的各点合并；（3）理想电流表可认为短路，理想电压表可认为断路；（4）电压稳定时，电容器可认为断路；（5）在电路中，若只有一处接地线，则只影响电路中各点的电势值，不影响电路结构和任意两点间的电势差；若电路中有两处或两处以上接地线，则除了影响电路中各点的电势外，还将改变电路结构，接地点之间认为是接在同一点.4．电路等效的常用方法与操作步骤⑴电流分支法：a.先将各节点标上字母；b.判定各支路元件的电流方向（若电路原来无电流，可假设在总电路两端加上电压后判断）；c.按电流流向，自左向右将各元件、节点、分支逐一画出；d.将画出的等效图加工整理.⑵等势点排列法： 简化图1图2。

学科教师辅导教案学员编号： 年 级： 课 时 数：1 学员姓名： 辅导科目：物理 学科教师： 授课内容 混联电路初步星 级 ★★★授课日期及时段教学内容电阻的连接方法有哪些？如何求得它们的总电阻呢？（以三个电阻为例） ①串联 ②并联实际工作和生活中，单纯的串联或并联电路是很少见的。

而最为常见的是混联电路。

也就是，既有电阻串联，又有电阻并联的电路，称为电阻混联电路。

2、混联电路进行等效变换的两种方法是：Ⅰ.课堂导入123R R R R =++总1231111R R R R =++总①利用电流的流向及电流的分、合，画出等效电路图； ②利用电路中各等电位点分析电路，画出等效电路图。

一、要点提纲：1、电阻的混联：既有电阻的串联，又有电阻的并联。

哪位同学愿意和我一起分析这个 电路各个电阻之间的串并联关系 呢？2、混联电路的等效电路图a.先在原电路图中，给每一个连接点标上字母。

b.同一导线相连的各连接点最好用同一字母3，沿着电源顺藤摸瓜 (注意两个图的对应关系）Ⅱ.同步讲解R 1R 2 R 3 R 4R 5E可是有些电路很调皮，不想我们直接看出各个元件之间的串并联关系，那我们该怎么办呢？ R1R3R4R2ER5因为同一导线上的电位是相等的啊R1 R3R4R2ER5 a abbR5a R1 R2 R3 R4bE4、混联电路等效电阻的计算如上图，如果R1=R2=R3=R4=50Ω;R5=30Ω，那这个闭合电路的总等效电阻是多少？二．题型分类：题型一：混联电路相关计算【例1】（★★★）如图所示，已知R 1 = R 2 = 8 Ω，R 3 = R 4 = 6 Ω，R 5 = R 6 = 4 Ω，R 7 = R 8 = 24 Ω，R 9 = 16 Ω；电压U = 224 V 。

试求：(1) 电路总的等效电阻R AB 与总电流I ∑；(2) 电阻R 9两端的电压U 9与通过它的电流I 9。

【解析】(1) R 5、R 6、R 9三者串联后，再与R 8并联，E 、F 两端等效电阻为R EF = (R 5 + R 6 + R 9)∥R 8 = 24 Ω∥24 Ω = 12 Ω R EF 、R 3、R 4三者电阻串联后，再与R 7并联，C 、D 两端等效电阻为 R CD = (R 3 + R EF + R 4)∥R 7 = 24 Ω∥24 Ω = 12 Ω 总的等效电阻 R AB =R 1 + R CD + R 2 = 28 Ω 总电流 I ∑ = U /R AB = 224/28 = 8 A(2)利用分压关系求各部分电压：U CD =R CD I ∑ = 96V ， V32 A 2V48962412999965EF9CD 4EF 3EF EF ===++==⨯=++=I R U R R R U I U R R R R U ，【例2】（★★★）如图所示，已知R = 10 Ω，电源电动势E = 6 V ，内阻r = 0.5 Ω，试求电路中的总电流I 。

画等效电路图的方法：一般混联电路比较复杂，在题目中出现时，有时故意将电路图形抽象化、隐蔽化，使我们不易很快看出串并联关系，画“等效电路”就是对比较复杂的电路运用串并联电路的知识进行分析，画出简明的等效电路，这种科学方法即“等效替代”的方法。

将比较复杂的电路画成简明的等效电路是电路计算中十分重要的第一步。

画等效电路图时，应遵循以下四个原则：⑴从电流流过的电路去识别电路结构。

电阻或用电器串并联是相对于电路中两端点而言的，各电阻中通过同一电流，则这些电阻是串联的；从某点起电流分开流过几个电阻后又汇合，这些电阻是并联的。

⑵在没有特殊说明时，电表均以理想电表看待，即电流表内阻为零；电压表内阻为无穷大。

⑶连接的导线不计电阻，导线上各点的电势相等，所以导线的长度可任意伸缩。

⑷无电流的支路化简时可去除。

例1：如图9-A2-5，R 1=R 3=2Ω，R 2=5Ω，R 4=3Ω， AB 间的电压为9V 。

求图中伏特表和安培表的读数。

[分析和解]这是一个有四个电阻的电路。

要画出它的等效电路图，我们假定电流从A 点流入，到C 点后电流只能由C 点经R 1流到D 点，因EF 之间接伏特表相当于断路；电流至D 点后，分为二路，一路经R 3、A 表、R 4到H 点，另一路经R 2到H 点，所以可看出R 3与R 4是串联关系，R 3、R 4串联后与R 2并联，再跟R 1串联。

安培表测的是经过R 3、R 4的电流，伏特表测的是R 1与R 3间电压（C 、F 两点的电压）。

图9-A2-5的等效电路图如图9-A2-6所示。

Ω=+543R R Ω=+++=5.2)()(243243R R R R R R R DHA R U I AB 25.4/9/1===总因43R R +与2R 相等，)(121234A I I I === ， ∴ A 表读数为1A V R I R I U U U CF 621223341131=⨯+⨯=+=+=， 所以V 表读数为6V 。