第25讲 Z变换及脉冲传递函数
- 格式:ppt
- 大小:930.00 KB
- 文档页数:35

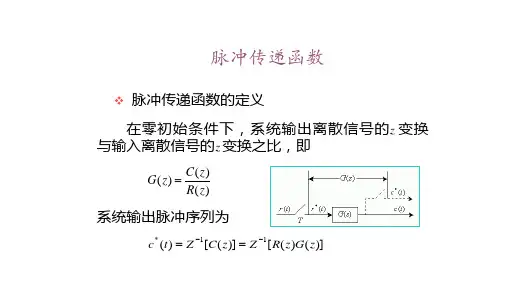



脉冲传递函数g(z)脉冲传递函数g(z)是一种常见的信号处理工具,它可以用于描述一种线性系统对输入脉冲信号的响应。
在工程研究中,脉冲传递函数g(z)在控制工程、通信系统、网络处理等领域中得到了广泛应用。
下面我们将从定义、性质、应用等方面来详述脉冲传递函数g(z)。
一、定义脉冲传递函数g(z)是指在离散时间下,单位脉冲信号经过线性系统后所得到的系统响应的比例函数。
数学上,脉冲传递函数可以表示为:g(z) = Y(z)/X(z)其中,Y(z)表示输出信号的Z变换,X(z)表示输入信号的Z变换。
二、性质1. 线性性:脉冲传递函数g(z)具有线性性质,即当输入信号是信号1、信号2的线性组合时,输出信号也是对应的线性组合。
2. 时不变性:当输入信号延迟m个时间单位时,输出信号也会延迟相同的m个时间单位。
3. 卷积性质:当有两个系统的脉冲传递函数分别为g1(z)和g2(z)时,它们的卷积g(z) = g1(z) g2(z)三、应用脉冲传递函数g(z)在工程实践中有很多应用,如下面几个方面:1. 控制工程:在控制系统设计中,脉冲传递函数g(z)用于描述控制器、传感器等系统的特性,以达到控制系统的设计目标。
2. 通信系统:在数字通信系统中,脉冲传递函数g(z)是一个能够描述信道传输特性的关键参数,可以用于设计调制解调器、信道均衡器等模拟信号处理器件。
3. 网络处理:在计算机网络处理中,脉冲传递函数g(z)可以描述网络传输的延迟、带宽等重要参数,以提高网络传输的可靠性和效率。
总之,脉冲传递函数g(z)是一种非常重要的信号处理工具,它在信号处理和系统控制领域中被广泛应用。
我们需要深入学习和掌握脉冲传递函数的特性和应用,以提高自己的技能和工程实践水平。



z传递函数一、引言z传递函数是信号处理中常用的一种数学方法,用来描述信号在系统中传递的特性。
它是频率域和时域之间的桥梁,可以通过分析系统的z传递函数来了解信号在系统中的变换过程。
在本文中,我们将会详细介绍z传递函数的定义、性质和应用等内容。
二、z传递函数的定义z传递函数是一种离散时间系统的表示方法,它以z变换的形式来表示系统的输入和输出之间的关系。
z传递函数通常用H(z)表示,其中z是一个复数变量。
z传递函数可以将时域中的差分方程转换为频域中的代数方程,从而方便我们进行系统的分析与设计。
三、z传递函数的性质1. 稳定性对于稳定系统来说,其z传递函数的绝对值必须小于1,即有|H(z)|<1。
这是因为稳定系统的输出应该是有界的,不能出现无限增长的情况。
2. 因果性在因果系统中,z传递函数只有在对应的范围内才有定义。
一般而言,因果系统的z传递函数是有理函数,即可以表示为多项式之比。
因而在对z进行逆向z变换时,只需要考虑有理函数的极点和极点的位置。
3. 线性性z传递函数满足线性性质,即对于任意的输入序列x(n)和y(n),以及对应的输出序列y(n)和z(n),如果存在k1和k2为常数,则有k1x(n) + k2y(n) -> k1y(n)+ k2z(n)。
4. 延时特性z传递函数中的延时特性能够直观地反映系统的时延情况。
通过分析z传递函数的分母项,可以确定系统的时延。
四、z传递函数的应用z传递函数在信号处理中有着广泛的应用,下面列举了几个常见的应用领域。
1. 滤波器设计在数字滤波器的设计过程中,z传递函数可以帮助我们分析和设计滤波器的频率响应特性。
通过调整z传递函数的系数,我们可以实现不同的滤波器类型,如低通滤波器、高通滤波器、带通滤波器等。
2. 系统控制z传递函数也被广泛应用于控制系统的设计与分析中。
通过建立系统的z传递函数模型,我们可以分析系统的稳定性、性能等指标,并进行控制器的设计与调整。



脉冲传递函数脉冲传递函数(Impulse Response)是一种数学概念,用于描述线性时不变(LTI)系统对于脉冲输入信号的响应。
在实际应用中,LTI系统常用于滤波、均衡、信号传输等领域,而脉冲传递函数是分析和设计这些系统的重要工具之一。
脉冲传递函数通常用h(t)表示,是一个响应脉冲输入信号单位脉冲(或单位斜坡)的连续时间函数。
当LTI系统接收到一个脉冲信号(即只在一个时刻上有信号,其余时刻信号为0),其输出信号即为该系统的脉冲响应。
脉冲响应描述了系统对于不同频率的信号输入的滤波响应,因此是分析系统性能和设计滤波器等应用中的重要指标。
对于一个离散时间系统,类似于连续时间系统,脉冲传递函数可以表示为一个响应单位脉冲输入信号的离散时间函数。
脉冲传递函数可以用公式表达为:h(t)=L^{-1} \{H(s)\}H(s)是系统的传递函数,L^{-1}表示拉普拉斯反变换。
对于离散时间系统,同样可用Z变换及反变换表示脉冲传递函数,即:h(n)=\frac {1}{2π j} \oint_C H(z) z^{n-1} dzH(z)是系统的传递函数,C是一条限定了积分路径的封闭曲线,n为离散时间点。
脉冲传递函数的使用脉冲传递函数可以用于分析和设计LTI系统。
利用脉冲传递函数,可以计算系统对于任意输入信号的响应。
对于任意输入信号,可以将其表示为单位脉冲序列的线性组合。
假设输入信号为x(t),其可以表示为x(t)=\int_{-\infty}^\infty x(\tau) \delta(t-\tau) d\tau\delta(t)为单位脉冲函数。
利用线性性质,可以将其转化为单位脉冲响应的组合形式:y(t)=\int_{-\infty}^\infty x(\tau) h(t-\tau) d\tauh(t)为系统的脉冲传递函数。
根据卷积公式,可以得到输出信号y(t)为y(t)=x(t)*h(t)*表示卷积运算。
通过计算脉冲传递函数,可以得到系统对于任意输入信号的响应。