闭环脉冲传递函数共127页
- 格式:ppt
- 大小:10.66 MB
- 文档页数:127





第八章 脉冲传递函数及性能分析分析线性定常线性离散系统时,脉冲传递函数也是一个很重要的概念,线性定常线性离散系统的动态特性可以由脉冲传递函数来描述。
通过脉冲传递函数,可以对线性定常线性离散系统的性能进行分析。
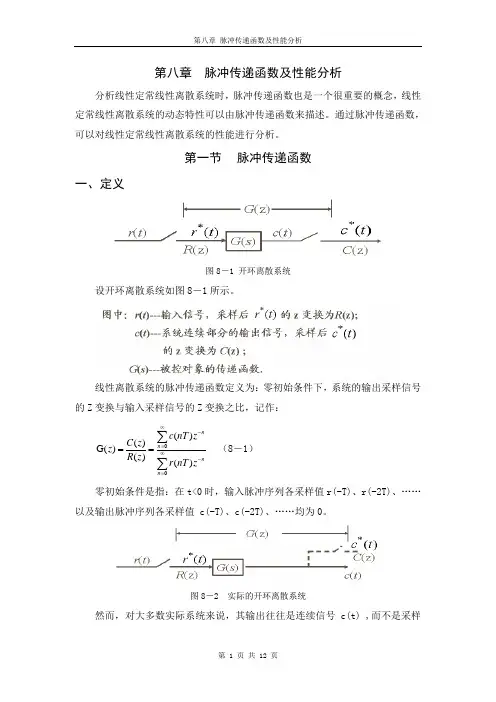
第一节 脉冲传递函数一、定义图8-1 开环离散系统设开环离散系统如图8-1所示。
线性离散系统的脉冲传递函数定义为:零初始条件下,系统的输出采样信号的Z 变换与输入采样信号的Z 变换之比,记作:()()G ()()()nn nn c nT zC z z R z r nT z∞-=∞-===∑∑ (8-1)零初始条件是指:在t<0时,输入脉冲序列各采样值r(-T)、r(-2T)、……以及输出脉冲序列各采样值 c(-T)、c(-2T)、……均为0。
图8-2 实际的开环离散系统然而,对大多数实际系统来说,其输出往往是连续信号 c(t) ,而不是采样信号*()c t,如图8-2所示。
此时,可以在系统输出端虚设一个理想采样开关,如图8-2中虚线所示。
它与输入采样开关同步工作,并具有相同的采样周期。
如果系统的实际输出c(t)比较平滑,且采样频率较高,则可由*()c t近似描述c(t)。
必须指出,虚设的采样开关是不存在的,它只是表明了脉冲传递函数所能描述的,只是输出连续函数在采样时刻上的离散值*()c t。
二、脉冲传递函数的求法1、由差分方程求(1)令初始条件为零,对差分方程两边作为z变换(查z变换表及用z变换定理);(2)据脉冲传递函数的定义G(z)=C(z)/R(z),求出脉冲传递函数G(z)。
2、由系统方块图求脉冲传递函数同样可以用方块图表示。
求取脉冲传递函数时,可以利用方块图变换来实现。
但是,在离散系统的方块图中,除了信号线、函数方块、引出点和比较点,还增加了采样开关。
连续系统的方块图分析法,不能照搬到离散系统。
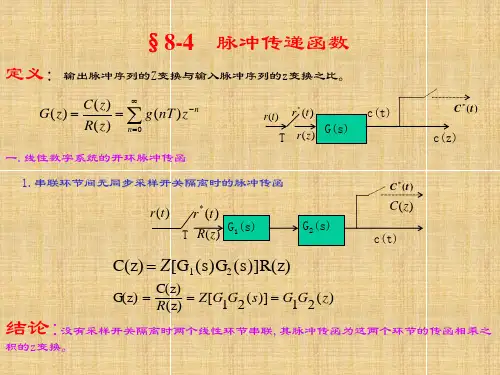
第二节开环系统脉冲传递函数一、串联环节1、离散环节串联——串联环节之间有采样开关等效的脉冲传递函数等于各环节脉冲传递函数之乘积,即G(z)=Z[G1(s)]*Z[G2(s)]=G1(z)G2(z) 图8-3 离散环节串联2、连续环节串联——串联环节之间无采样开关等效的脉冲传递函数等于各环节传递函数乘积之z变换,即G(z)=Z[G1(s)G2(s)]= G1G2(z)。

永磁同步电机闭环控制的传递函数【最新版】目录一、永磁同步电机闭环控制的概述二、永磁同步电机闭环控制的传递函数1.传递函数的定义2.永磁同步电机闭环控制中的传递函数3.传递函数的应用三、永磁同步电机闭环控制的设计方法1.控制系统的设计2.控制器的设计3.控制算法的设计四、永磁同步电机闭环控制的性能分析1.控制系统的稳定性分析2.控制器的性能分析3.控制算法的性能分析五、永磁同步电机闭环控制的应用实例1.永磁同步电机的位置控制2.永磁同步电机的转速控制3.永磁同步电机的矢量控制六、永磁同步电机闭环控制的发展趋势1.控制理论的发展2.控制算法的优化3.应用领域的扩展正文一、永磁同步电机闭环控制的概述永磁同步电机(Permanent Magnet Synchronous Motor,简称 PMSM)是一种采用永磁材料作为磁场源的同步电机,具有高效率、高功率因数、低噪音等优点,在工业、航空航天、交通运输等领域得到广泛应用。
为了实现对永磁同步电机的精确控制,需要采用闭环控制技术。
闭环控制是指通过将系统的输出反馈到输入端,对系统进行实时调节,以达到预定的控制目标。
永磁同步电机闭环控制主要包括电流控制、转速控制和矢量控制等。
二、永磁同步电机闭环控制的传递函数1.传递函数的定义传递函数是指系统输出与输入之间的传递关系,用以描述系统对输入信号的响应特性。
在永磁同步电机闭环控制中,传递函数主要用于分析系统的稳定性和动态性能。
2.永磁同步电机闭环控制中的传递函数永磁同步电机闭环控制的传递函数主要包括电流环传递函数、转速环传递函数和矢量控制环传递函数。
这些传递函数分别描述了电流、转速和磁场等控制变量对永磁同步电机输出力的影响关系。
3.传递函数的应用传递函数在永磁同步电机闭环控制中的应用主要体现在以下几个方面:(1) 分析系统的稳定性:通过分析传递函数的极点与零点分布,可以判断系统是否稳定,以及稳定范围内的动态性能。
(2) 设计控制器:根据传递函数的特性,可以设计合适的控制器,以实现对永磁同步电机的精确控制。



脉冲传递函数脉冲传递函数(Impulse Response)是一种数学概念,用于描述线性时不变(LTI)系统对于脉冲输入信号的响应。
在实际应用中,LTI系统常用于滤波、均衡、信号传输等领域,而脉冲传递函数是分析和设计这些系统的重要工具之一。
脉冲传递函数通常用h(t)表示,是一个响应脉冲输入信号单位脉冲(或单位斜坡)的连续时间函数。
当LTI系统接收到一个脉冲信号(即只在一个时刻上有信号,其余时刻信号为0),其输出信号即为该系统的脉冲响应。
脉冲响应描述了系统对于不同频率的信号输入的滤波响应,因此是分析系统性能和设计滤波器等应用中的重要指标。
对于一个离散时间系统,类似于连续时间系统,脉冲传递函数可以表示为一个响应单位脉冲输入信号的离散时间函数。
脉冲传递函数可以用公式表达为:h(t)=L^{-1} \{H(s)\}H(s)是系统的传递函数,L^{-1}表示拉普拉斯反变换。
对于离散时间系统,同样可用Z变换及反变换表示脉冲传递函数,即:h(n)=\frac {1}{2π j} \oint_C H(z) z^{n-1} dzH(z)是系统的传递函数,C是一条限定了积分路径的封闭曲线,n为离散时间点。
脉冲传递函数的使用脉冲传递函数可以用于分析和设计LTI系统。
利用脉冲传递函数,可以计算系统对于任意输入信号的响应。
对于任意输入信号,可以将其表示为单位脉冲序列的线性组合。
假设输入信号为x(t),其可以表示为x(t)=\int_{-\infty}^\infty x(\tau) \delta(t-\tau) d\tau\delta(t)为单位脉冲函数。
利用线性性质,可以将其转化为单位脉冲响应的组合形式:y(t)=\int_{-\infty}^\infty x(\tau) h(t-\tau) d\tauh(t)为系统的脉冲传递函数。
根据卷积公式,可以得到输出信号y(t)为y(t)=x(t)*h(t)*表示卷积运算。
通过计算脉冲传递函数,可以得到系统对于任意输入信号的响应。