频率特性1
- 格式:ppt
- 大小:672.50 KB
- 文档页数:31


一、实验目的1. 理解频率特性的基本概念和测量方法。
2. 掌握使用Bode图和尼奎斯特图分析系统频率特性的方法。
3. 了解频率特性在系统设计和稳定性分析中的应用。
二、实验原理频率特性描述了系统对正弦输入信号的响应,通常用幅频特性和相频特性来表示。
幅频特性表示输出信号幅度与输入信号幅度之间的关系,相频特性表示输出信号相位与输入信号相位之间的关系。
频率特性的测量通常通过以下步骤进行:1. 使用正弦信号发生器产生不同频率的正弦信号。
2. 将信号输入被测系统,并测量输出信号的幅度和相位。
3. 根据测量数据绘制幅频特性和相频特性曲线。
三、实验设备1. 正弦信号发生器2. 示波器3. 信号分析仪4. 被测系统(如电路、控制系统等)四、实验步骤1. 准备实验设备,确保各设备连接正确。
2. 设置正弦信号发生器,产生一系列不同频率的正弦信号。
3. 将正弦信号输入被测系统,并使用示波器或信号分析仪测量输出信号的幅度和相位。
4. 记录不同频率下的幅度和相位数据。
5. 使用绘图软件绘制幅频特性和相频特性曲线。
五、实验结果与分析1. 幅频特性分析通过绘制幅频特性曲线,可以观察到系统对不同频率信号的衰减程度。
一般来说,低频信号的衰减较小,高频信号的衰减较大。
根据幅频特性,可以判断系统的带宽和稳定性。
2. 相频特性分析通过绘制相频特性曲线,可以观察到系统对不同频率信号的相位延迟。
相频特性曲线通常呈现出滞后或超前特性。
根据相频特性,可以判断系统的相位裕度和增益裕度。
3. 系统稳定性分析根据幅频特性和相频特性,可以判断系统的稳定性。
如果系统的相位裕度和增益裕度都大于零,则系统是稳定的。
否则,系统可能是不稳定的。
六、实验结论通过本次实验,我们成功地测量了被测系统的频率特性,并分析了其幅频特性和相频特性。
实验结果表明,被测系统在低频段表现出较小的衰减,而在高频段表现出较大的衰减。
相频特性曲线显示出系统在低频段滞后,在高频段超前。
根据频率特性分析,可以得出被测系统是稳定的。
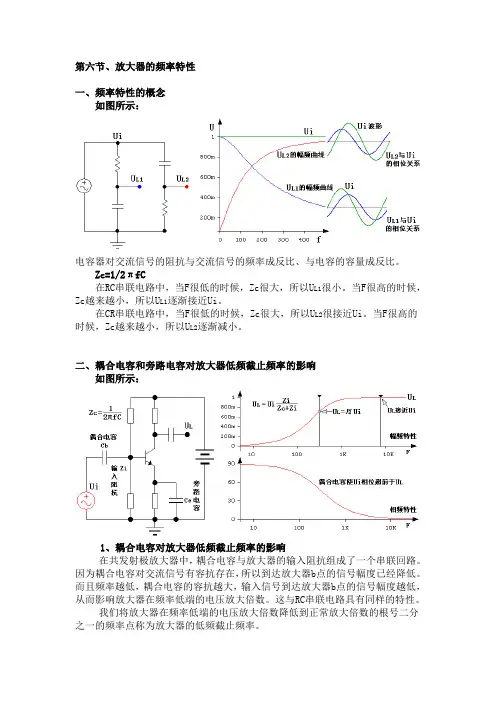
第六节、放大器的频率特性一、频率特性的概念如图所示:电容器对交流信号的阻抗与交流信号的频率成反比、与电容的容量成反比。
Zc=1/2πfC在RC串联电路中,当F很低的时候,Zc很大,所以U L1很小。
当F很高的时候,Zc越来越小,所以U L1逐渐接近Ui。
在CR串联电路中,当F很低的时候,Zc很大,所以U L2很接近Ui。
当F很高的时候,Zc越来越小,所以U L2逐渐减小。
二、耦合电容和旁路电容对放大器低频截止频率的影响如图所示:1、耦合电容对放大器低频截止频率的影响在共发射极放大器中,耦合电容与放大器的输入阻抗组成了一个串联回路。
因为耦合电容对交流信号有容抗存在,所以到达放大器b点的信号幅度已经降低。
而且频率越低,耦合电容的容抗越大,输入信号到达放大器b点的信号幅度越低,从而影响放大器在频率低端的电压放大倍数。
这与RC串联电路具有同样的特性。
我们将放大器在频率低端的电压放大倍数降低到正常放大倍数的根号二分之一的频率点称为放大器的低频截止频率。
2、旁路电容对放大器低频截止频率的影响旁路电容对放大器低频截止频率的影响与耦合电容具有同样的原理,只是从放大器三极管发射极看进去的阻抗;与基极看进去的阻抗相差β倍,因此,同样容量的电容器,发射极电容比基极电容对放大器低频特性的影响要大β倍。
所以,耦合电容和旁路电容影响的都是放大器的低频截止频率。
三、影响放大器高频截止频率的因素电子线路的分布电容对放大器高频截止频率的影响最为显著。
1、三极管的极间电容三极管的三个电极之间都存在着分布电容Cce、Ccb、Cce。
这些分布电容的参数都很小,高频小功率三极管的基建电容通常在10PF以下。
在低频的时候容抗很大,对放大器频率特性的影响可以忽略不计。
当进入高频阶段以后,参数很小的分布电容的容抗逐渐减小,对放大器的高频特性越来越严重地产生根本性的制约。
如图A所示:2、分布电容对共发射极放大器高频信号放大能力的影响a、共发射极放大器输入高频信号的时候,基极与发射极之间的极间电容Cbe 会对输入信号产生对的分流的作用。




![Chapter5-1+频率特性的基本概念典型环节的频率特性[1]](https://uimg.taocdn.com/815d4f1476c66137ee0619cc.webp)



第5章线性系统的频域分析法5.1复习笔记本章考点:幅相特性曲线、伯德图的绘制,奈奎斯特稳定判据,稳定裕度计算。
一、频率特性1.定义幅频特性:稳态响应的幅值与输入信号的幅值之比A(ω)。
相频特性:稳态响应与正弦输入信号的相位差φ(ω)。
频率特性:幅频特性和相频特性在复平面上构成的一个完整向量G(jω)=A(ω)e jφ(ω)。
2.频率特性的几何表示法(重点)(1)幅相频率特性曲线(幅相曲线或极坐标图),横坐标为开环频率特性的实部,纵坐标为虚部, 为参变量。
(2)对数频率特性曲线(伯德图),由对数幅频特性曲线、对数幅相频特性曲线两幅图组成:①对数幅频特性曲线的纵坐标表示L(ω)=20lgA(ω),单位是分贝,记作dB;②对数相频特性曲线的纵坐标为φ(ω),单位为度“°”。
(3)对数幅相曲线(尼科尔斯图),横坐标表示频率特性的相角φ(ω),纵坐标表示频率特性的幅值的分贝数L(ω)=20lgA(ω)。
二、典型环节与开环系统的频率特性1.典型环节的频率特性一些主要典型环节的频率特性曲线总结如表5-1-1所示。
表5-1-1典型环节频率特性曲线总结2.开环幅相曲线绘制步骤(1)确定开环幅相曲线的起点(ω=0+)和终点(ω=∞),确定幅值变化与相角变化。
(2)计算开环幅相曲线与实轴的交点。
令Im[G(jωx)H(jωx)]=0或φ(ωx)=∠G(jωx)H(jωx)=kπ(k=0,±1,…)称ωx为穿越频率,而开环频率特性曲线与实轴交点的坐标值为Re[G(jωx)H(jωx)]=G(jωx)H(jωx)。
(3)分析开环幅相曲线的变化范围(象限、单调性)。
3.开环对数频率特性曲线绘制步骤(1)开环传递函数典型环节分解并确定一阶环节、二阶环节的交接频率;(2)绘制低频段渐近特性线:在ω<ωmin频段内,直线斜率为-20vdB/dec;(3)作ω≥ωmin频段渐近特性线,交接频率点处斜率变化表如表5-1-2所示。