二次方程根的分布情况归纳(教师版)

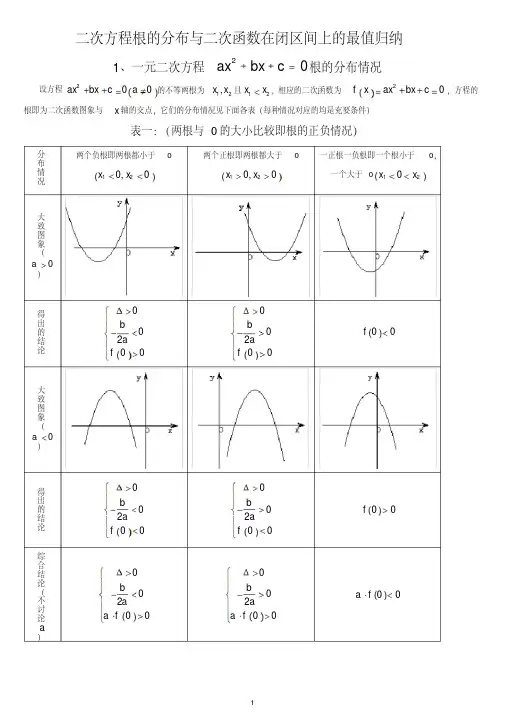
2015届高三一轮复习讲义课题：二次函数一、教学目标：掌握二次函数的概念、图象及性质；能利用二次函数研究一元二次方程的实根分布条件；能求二次函数的区间最值．二、教学重点：二次函数、一元二次方程及一元二次不等式之间的灵活转化． 三、教学过程： （一）主要知识：1、二次函数的定义：形如)0(2≠++=a c bx ax y 的函数叫做二次函数， 2、二次函数的解析式的三种形式： 一般式)0()(2≠++=a c bx ax x f ， 顶点式)0()()(2≠+-=a n m x a x f ， 两根式)0)(()()(21≠-⋅-=a x x x x a x f ．3、二次函数的图象及性质：二次函数)0(2≠++=a c bx ax y 的图象的对称轴方程是abx 2-=，顶点坐标是⎪⎪⎭⎫ ⎝⎛--a b ac a b 4422， 4、二次函数、一元二次方程及一元二次不等式之间的关系． （二）主要方法：1、讨论二次函数的区间最值问题：①注意对称轴与区间的相对位置；②函数在此区间上的单调性；2、讨论二次函数的区间根的分布情况一般需从三方面考虑：①判别式；②区间端点的函数值的符号；③对称轴与区间的相对位置． （三）例题分析：例1．函数2([0,))y x bx c x =++∈+∞是单调函数的充要条件是（ A ） ()A 0b ≥ ()B 0b ≤ ()C 0b > ()D 0b <分析：对称轴2b x =-，∵函数2([0,)y x bx c x =++∈+∞是单调函数，∴对称轴2b x =-在区间 [0,)+∞的左边，即02b-≤，得0b ≥．例2．已知二次函数的对称轴为x =x 轴上的弦长为4，且过点(0,1)-，求函数的解析式．解：∵二次函数的对称轴为x =2()(f x a x b =+，又∵()f x 截x 轴上的弦长为4，∴()f x过点(2,0)+，()f x 又过点(0,1)-，∴4021a b a b +=⎧⎨+=-⎩， 122a b ⎧=⎪⎨⎪=-⎩，∴21()(22f x x =+-． 例3．已知函数21sin sin 42a y x a x =-+-+的最大值为2，求a 的值 ． 分析：令sin t x =，问题就转二次函数的区间最值问题． 解：令sin t x =，[1,1]t ∈-，∴221()(2)24a y t a a =--+-+，对称轴为2at =，（1）当112a -≤≤，即22a -≤≤时，2max 1(2)24y a a =-+=，得2a =-或3a =（舍去）．（2）当12a >，即2a >时，函数221()(2)24a y t a a =--+-+在[1,1]-单调递增，由max 111242y a a =-+-+=，得103a =．（3）当12a <-，即2a <-时，函数221()(2)24a y t a a =--+-+在[1,1]-单调递减， 由max 111242y a a =---+=，得2a =-（舍去）．综上可得：a 的值为2a =-或103a =．例4． 已知函数22()(21)2f x x a x a =--+-与非负x 轴至少有一个交点，求a 的取值范围．解法一：由题知关于x 的方程22(21)20x a x a --+-=至少有一个非负实根，设根为12,x x则120x x ≤或121200x x x x ∆≥⎧⎪>⎨⎪+>⎩，得94a ≤≤．解法二：由题知(0)0f ≤或(0)0(21)020f a >⎧⎪--⎪->⎨⎪∆≥⎪⎩，得94a ≤≤．例5．对于函数()f x ，若存在0x R ∈，使00()f x x =，则称0x 是()f x 的一个不动点，已知函数2()(1)(1)(0)f x ax b x b a =+++-≠，（1）当1,2a b ==-时，求函数()f x 的不动点；（2）对任意实数b ，函数()f x 恒有两个相异的不动点，求a 的取值范围；（3）在（2）的条件下，若()y f x =的图象上,A B 两点的横坐标是()f x 的不动点，且,A B 两点关于直线2121y kx a =++对称，求b 的最小值． 解：（1）2()3f x x x =--，0x 是()f x 的不动点，则2000()3f x x x x =--=，得01x =-或03x =，函数()f x 的不动点为1-和3．（2）∵函数()f x 恒有两个相异的不动点，∴2()(1)0f x x ax bx b -=++-=恒有两个不等的实根，224(1)440b a b b ab a ∆=--=-+>对b R ∈恒成立，∴2(4)160a a -<，得a 的取值范围为(0,1)．（3）由2(1)0ax bx b ++-=得1222x x b a +=-，由题知1k =-，2121y x a =-++， 设,A B 中点为E ，则E 的横坐标为21(,)2221b b a a a -++，∴212221b b a a a -=++，∴2112142a b a a a =-=-≥-++，当且仅当12(01)a a a =<<，即2a =时等号成立，∴b的最小值为（四）巩固练习：1．若函数2(2)3([,]y x a x x a b =+++∈的图象关于1x =对称则b = 6 ．2．二次函数()f x 的二次项系数为负值，且(2)(2)()f x f x x R +=-∈，问2(12)f x -与2(12)f x x +-满足什么关系时，有20x -<<．3．m 取何值时，方程227(13)20x m x m m -++--=的一根大于1，一根小于1．专题：二次方程根的分布与二次函数在闭区间上的最值归纳1、一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）k k k根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩； （2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩对以上的根的分布表中一些特殊情况作说明： （1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

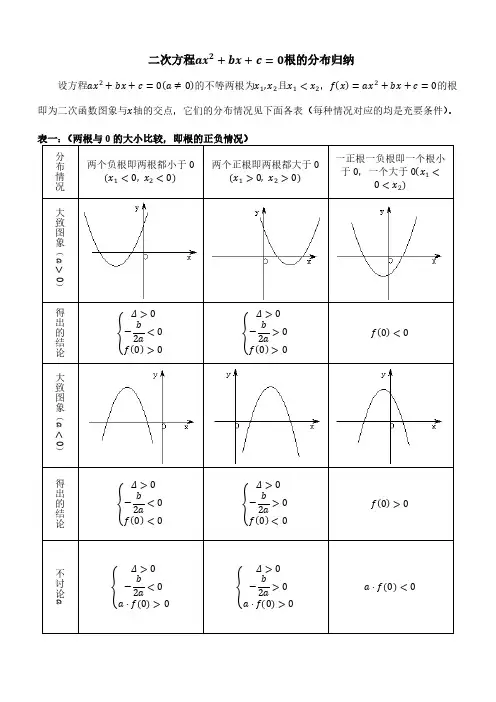
二次方程ax2+bx+c=0根的分布归纳设方程ax2+bx+c=0(a≠0)的不等两根为x1,x2且x1<x2，f(x)=ax2+bx+c=0的根即为二次函数图象与x轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）。

k k k况f(m)>0根在区间上的分布还有一种情况：两根分别在区间(m,n )外，即在区间两侧x 1<m,x 2>n ，（图形分别如下）需满足的条件是（1）a >0时，{f (m )<0f (n )<0； （2）a <0时，{f (m )>0f (n )>0两根有且仅有一根在(m,n )内有以下特殊情况：1°若f (m )=0或f (n )=0，则此时f (m )f (n )<0不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间(m,n )内，从而可以求出参数的值。

如方程mx 2−(m +2)x +2=0在区间(1,3)上有一根，因为f (1)=0，所以mx 2−(m +2)x +2=(x −1)(mx −2)，另一根为2m ，由1<2m <3得23<m <2即为所求；2°方程有且只有一根，且这个根在区间(m,n )内，即Δ=0，此时由Δ=0可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给定的区间内，如若不在，舍去相应的参数。

如方程x 2−4mx +2m +6=0有且一根在区间(−3,0)内，求m 的取值范围。

分析：①由f (−3)f (0)<0即(14m +15)(m +3)<0得出−3<m <−1514；②由Δ=0即16m 2−4(2m +6)=0得出m =−1或m =32，当m =−1时，根x =−2∈(−3,0)，即m =−1满足题意；当m =32时，根x =3∉(−3,0)，故m =32不满足题意；综上分析，得出−3<m <−1514或m =−1根的分布练习题例1、已知二次方程(3m+1)x2−2mx+(m−1)=0有一正根和一负根，求实数m的取值范围.例2、已知二次方程(2m+1)x2−5mx+(3m+1)=0有两个正根，求实数m的取值范围.例3、已知二次方程(3m+2)x2−mx+(m−1)=0有两个负根，求实数m的取值范围.例4、已知二次方程2x2−(m+1)x+m=0有两个不等正实根，求实数m的取值范围.例5、已知二次方程(m+2)x2−(2m+4)x+(3m+3)=0有两个根分别分布在(0,1)和(2,3)范围内，求实数m的取值范围.例6、已知二次方程2mx2+(2m−3)x+4m=0只有一个正根且这个根小于1，求实数m的取值范围.例7、求实数m范围，使得关于x的方程mx2+2(m−1)x+2m+6=0.（1）有两个实数根，且一个比2大，一个比2小.（2）有两个实数根α，β，5且满足0<α<1<β<4.（3）至少有一个正根.例8、已知方程m·22x+(2m−1)·2x+m=0在(−∞，1)上有两个根，求m的取值范围.。

一元二次方程根的分布情况归纳总结一元二次方程ax+bx+c=0的根的分布情况可以通过二次函数f(x)=ax^2+bx+c的图象与x轴的交点的横坐标来确定。

设方程的不等两根为x1和x2，且x1<x2.下面分别讨论根的分布情况。

表一：两根与0的大小比较即根的正负情况(a>0)分布情况两个负根即x1<x2<0 两个正根即0<x1<x2 一正根一负根即一个根小于0，一个大于0大致图象结论Δ>0，b0，b>0 f(x)>0 x1和x2都是正数f(0)>0 x1<0<x2表二：两根与k的大小比较(a>0)分布情况两根都小于k即x1x2>k 一个根小于k，一个大于k即x1<k<x2大致图象结论Δ>0，b0 x1<k<x2Δ>0，b>k f(k)>0 x1>x2>kf(k)>0 x1<k<x2表三：根在区间上的分布(a>0)分布情况两根都在(m,n)内一根在(m,n)内，另一根在(p,q)内两根有且仅有一根在(m,n)内，m<n<p<q（图象有两种情况，只画了一种）大致图象结论Δ>0，f(m)>0，f(n)>0 m<n<x1<x2<p<qΔ>0，f(m)>0，f(n)0 x1<m<n<x2<p<qΔ>0，f(m)0，f(p)>0，f(q)<0 m<n<x1<p<q<x2 或x1<m<n<q<p<x2函数与方程思想：1) 方程f(x)=0有根⇔y=f(x)与x轴有交点x⇔函数y=f(x)有零点x2) 若y=f(x)与y=g(x)有交点(x,y)⇔f(x)=g(x)有解x根的分布练题例1、已知二次方程(2m+1)x^2-2mx+(m-1)=0有一正根和一负根，求实数m的取值范围。

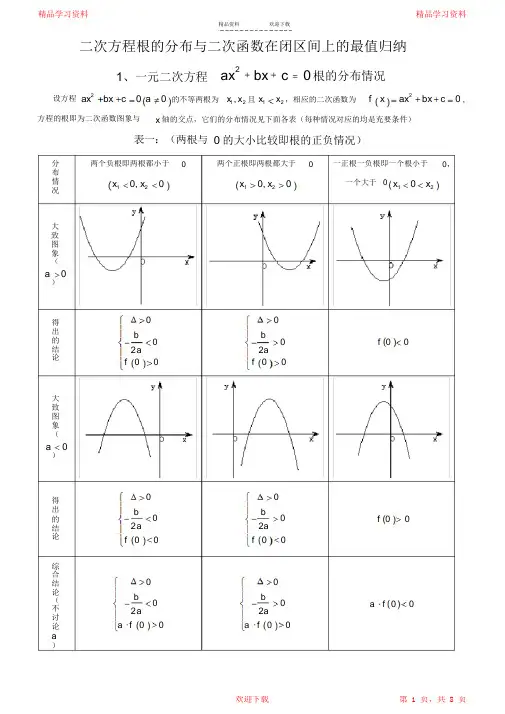
二次方程根的分布与二次函数在闭区间上的最值归纳ax2bx c 0 根的分布情况1、一元二次方程ax2ax2bx c 0 a 0 f x bx c 0 ，设方程x , x x x的不等两根为且，相应的二次函数为1 2 12方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0 的大小比较即根的正负情况）分布情况两个负根即两根都小于两个正根即两根都大于一正根一负根即一个根小于0，00一个大于0 x10, x20x10, x20x10x2大致图象（a0）00得出的结论b2 ab2a00 f 00f 0 f 0大致图象（a0）00得出的结论b2 ab2a00 f 00f 0 f 0综合结论（不讨论a ）00b2 ab2a00a f 0 0 a f 00a f 00k k 即k 即分 布 情 况一个根小于k ，一个大于 两根都小于即两根都大于x 1 k, x 2 kx 1k, x 2kx 1kx 2大 致 图 象 （kkka 0）0 0 得 出 的 结 论b 2a kb 2a kk k f kf 0f 0大 致 图 象 （a 0）0 0 得 出 的 结 论b 2 a kb 2a kk k f kf 0f 0综 合 结 论 （ 不 讨 论a）0 0b 2a b2a k k a f ka f ka f k分布情况m, n m,n 内，另一根在p, q两根有且仅有一根在内一根在m, n两根都在内m n p q内，（图象有两种情况，只画了一种）大致图象（a0）0 mnb 2a ffffmnpq得出的结论ffffmpffnq或f m f n0m n大致图象（a0）0 mnb 2a ffffmnpq得出的结论ffffmpffnq或f m f n0m n综合结论（不讨论a ）f m f n0f m f n0——————f p f q0m, n根在区间上的分布还有一种情况：两根分别在区间外，即在区间两侧x1m, x2n ，（图形分别如下）需满足的条件是f f m n0 0f f m n0 0（ 1） a0 时，；（ 2） a0 时，对以上的根的分布表中一些特殊情况作说明： （ 1）两根有且仅有一根在m, n 内有以下特殊情况：1 若 f m0或 fn0 ，则此时 f m f n 0 不成立， 但对于这种情况是知道了方程有一根为m 或 n ，mx2可以求出另外一根， 然后可以根据另一根在区间 m, n 内，从而可以求出参数的值。

二次方程根的分布与二次函数在闭区间上的最值归纳21、一元二次方程ax bx c 0根的分布情况设方程ax bx c 0 a 0的不等两根为X|,X2且X i x?，相应的二次函数为f x ax bx c 0，方程的根即为二次函数图象与x轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）根在区间上的分布还有一种情况：两根分别在区间夕卜，即在区间两侧为2,（图形分别如下）需满足的条件是f n 0 f n 0对以上的根的分布表中一些特殊情况作说明： (1)两根有且仅有一根在 m, n 有以下特殊情况：1 若f m 0或f n 0,则此时f mg f n 0不成立，但对于这种情况是知道了方程有一根为 m 或n ，可以求出另外一根， 然后可以根据另一根在区间 m,n ，从而可以求出参数的值。

如方程mx 2 m 2 x 2 0、 2 2 2在区间1,3上有一根，因为f 10，所以mx m 2 x 2 x 1 mx 2，另一根为 ，由13m m2得 m 2即为所求；3 2方程有且只有一根，且这个根在区间m, n ，即 0,此时由 0可以求出参数的值，然后再将参数的值带入方程，求出相应的根，检验根是否在给疋的区间， 如右不在，舍去相应的参数。

如方程x 4mx 2m 6 0有且 一根在区间 3,0 ,求m 的取值围。

分析：①由f 3gf 0 0 即 14m 15 m3 0得出 3 15 m；②由0即 16m 2 4 2m146 0得出m 31 或 m —,2 当m1时，根x23,0 ,即m31满足题意；当m 时，根x 323,0，故 m-不满足题意； 2综上分析，得出3 m至或14m1根的分布练习题例1、已知二次方程 2m 1 x 2 2mx m 1 0有一正根和一负根，数 m 的取值围。

1解：由 2m 1 gf 0 0即 2m 1 m 1 0，从而得m 1即为所求的围。

二次方程根的分布与二次函数在闭区间上的最值归纳
1、一元二次方程ax2 bx c 0根的分布情况
设方程ax2bx c 0 a 0的不等两根为x i,x2且x1 x2,相应的二次函数为f x ax2bx c 0,方程的根即为二次函数图象与x轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）
表一：（两根与0的大小比较即根的正负情况）
分布情况两个负根即两根都小于0
x1 0, x20
两个正根即两根都大于0
X 0, x20
一正根一负根即一个根小于0,
一个大于0 X1 0 x2
得出的结论得出的结
论综合结论
{不讨论a
2a
2a
表二：（两根与k的大小比较）
分布情况两根都小于k即
x1 k, x2k
两根都大于k即
x1 k, x2k
得出的
结论
2a f k
得出的结论综合结论{不讨论a
b k
2a
f k 0
2a
a f k 0
表三：（根在区间上的分布）
分布情况
o o
n q
f f m p f f
或
o o o
o
o
n n
o b a
t 2 n 得出的结论
o o
n q
f f m p f f
或
o o o
o
o
n
n
o o
b
m n f f m
得出的结论
综合结论{不讨论
a
m,n 夕卜，即在区间两侧 x i m,X 2 n,（图形分别如下）需满
根在区间上的分布还有一种情况：两根分别在区间
足的条件是。

二次方程()200axbx c a ++=≠根的分布一元二次方程02=++c bx ax 根的分布情况【一元二次方程根的分布的类型：】 1、零分布（1）有两正根 （2）有两负根 （3）一正一负2、k 分布（1）有两个大于k 的根 （2）有两个小于k 的根 （3）一个大于k,一个小于k, （4）有一个根在区间（k 1,k 2）内 （5）区间（k 1,k 2）有两个根 【引例】设方程的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）表一：（两根与0的大小比较即根的正负情况）分布情况两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象（>a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f大致图象（<a ）得出的结论()00200b a f ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()00200b a f ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()00>f综合结论（不讨论a）()00200b a a f ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()00200b a a f ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()00<⋅f a分布情况两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ，一个大于k 即21x k x <<大致图象（>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f大致图象（<a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪<⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪<⎪⎩ ()0>k f综合结论（不讨论a）()020b k a a f k ∆>⎧⎪⎪-<⎨⎪⋅>⎪⎩ ()020b k a a f k ∆>⎧⎪⎪->⎨⎪⋅>⎪⎩ ()0<⋅k f akkk分布情况两根都在()nm,内两根有且仅有一根在()nm,内（图象有两种情况，只画了一种）一根在()nm,内，另一根在()qp,内，qpnm<<<大致图象（0 > a）得出的结论()()2f mf nbm na∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅nfmf()()()()f mf nf pf q⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()f m f nf p f q<⎧⎪⎨<⎪⎩大致图象（0 < a）得出的结论()()2f mf nbm na∆>⎧⎪<⎪⎪<⎨⎪⎪<-<⎪⎩()()0<⋅nfmf()()()()f mf nf pf q⎧<⎪>⎪⎨>⎪⎪<⎩或()()()()f m f nf p f q<⎧⎪⎨<⎪⎩综合结论（不讨论a ）——————()()0<⋅nfmf()()()()⎪⎩⎪⎨⎧<<qfpfnfmf根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是（1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩； （2）0a <时，()()0f m f n >⎧⎪⎨>⎪⎩一元二次方程根的分布题型例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根，求实数m 的取值范围。

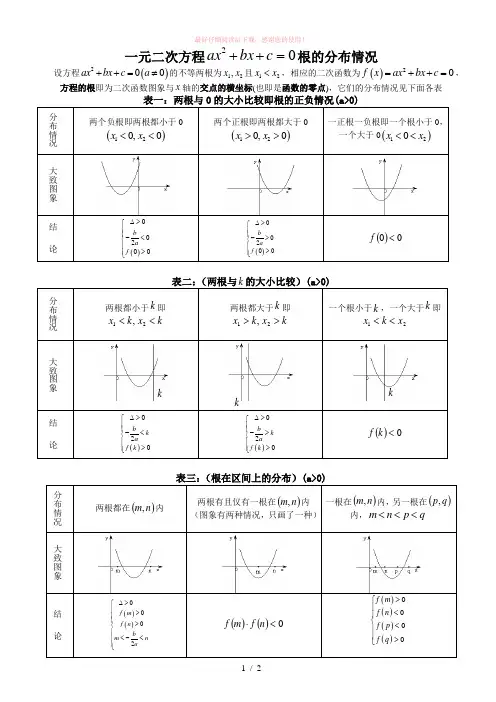
一元二次方程02=++c bx ax 根的分布情况 设方程()200ax bx c a ++=≠的不等两根为12,x x 且12x x <，相应的二次函数为()20f x ax bx c =++=，方程的根即为二次函数图象与x 轴的交点的横坐标(也即是函数的零点)，它们的分布情况见下面各表表一：两根与0的大小比较即根的正负情况(a>0)分布情况 两个负根即两根都小于0()120,0x x << 两个正根即两根都大于0()120,0x x >>一正根一负根即一个根小于0，一个大于0()120x x <<大致图象结论()00200ba f ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()00200ba f ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()00<f分布情况两根都小于k 即 k x k x <<21,两根都大于k 即 k x k x >>21,一个根小于k ，一个大于k 即21x k x <<大致图象结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f分布情况 两根都在()n m ,内两根有且仅有一根在()n m ,内（图象有两种情况，只画了一种）一根在()n m ,内，另一根在()q p ,内，q p n m <<< 大致图象结 论()()0002f m f n b m na ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩()()0<⋅n f m f()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩k kk函数与方程思想：（1）方程f (0x )=0有根⇔y =()f x 与x 轴有交点0x ⇔函数y=()f x 有零点0x （2）若y =f (x )与y =g (x )有交点(0x ，0y )⇔()f x =()g x 有解0x根的分布练习题例1、已知二次方程()()221210m x mx m +-+-=有一正根和一负根，求实数m 的取值范围。