高中数学：一元二次方程实根的分布

一元二次方程实数根的分布教学目标：使学生掌握一元二次方程实根分布问题的处理，加强求解一元二次不等式及不等式组，初步训练学生的数形结合能力。

教学重点：利用二次函数的图象，把一元二次方程根的分布−−→−转化图形问题−−→−转化代数表达式（不等式组）−−→−计算参数取值范围。

教学难点：图形问题转化成代数表达式(不等式组)并求解。

一．一元二次方程根的基本分布——零分布所谓一元二次方程根的零分布，指的是方程的根相对于零的关系。

比如二次方程有一正根，有一负根，其实就是指这个二次方程一个根比零大，一个根比零小，或者说，这两个根分布在零的两侧。

设一元二次方程02=++c bx ax （0≠a ）的两个实根为1x ，2x ，且21x x ≤。

1、两个正根⇔212124000b ac b x x a c x x a ⎧∆=-≥⎪⎪⎪+=->⎨⎪⎪=>⎪⎩， 2、两负根⇔⎪⎪⎪⎩⎪⎪⎪⎨⎧>=<-=+≥-=∆000421212a c x x a b x x ac b 3、一正根一负根 021<=acx x 4、一正根一负根，负根绝对值大⎪⎪⎩⎪⎪⎨⎧<=<-=+002121a c x x a b x x 5、一正根一负根，正根绝对值大⎪⎪⎩⎪⎪⎨⎧<=>-=+002121a c x x a b x x 6、有一根为0 0,0,021=>-==c abx x 例1：若方程0)5()2(2=++++m x m x有两正根，求实数m 的取值范围.变式1：两根两负？ 变式2: 两根一正一负？变式3: 两根一正一负，且正根绝对值大？ 变式4: 两根一正一负，且负根绝对值大？例2：若一元二次方程03)12(2=-+-+k x k kx 有一根为零，则另一根是正根还是负根？分析：由已知k －3=0，∴k =3，代入原方程得32x +5x =0，另一根为负。

二．一元二次方程的非零分布——k 分布设一元二次方程02=++c bx ax （0≠a ）的两实根为1x ，2x ，且21x x ≤。

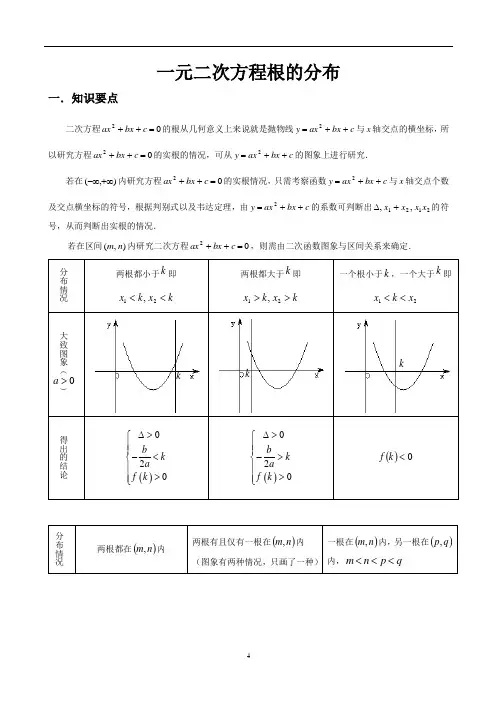
一元二次方程根的分布一．知识要点二次方程02=++c bx ax 的根从几何意义上来说就是抛物线c bx ax y ++=2与x 轴交点的横坐标，所以研究方程02=++c bx ax 的实根的情况，可从c bx ax y ++=2的图象上进行研究．若在),(+∞-∞内研究方程02=++c bx ax 的实根情况，只需考察函数c bx ax y ++=2与x 轴交点个数及交点横坐标的符号，根据判别式以及韦达定理，由c bx ax y ++=2的系数可判断出2121,,x x x x +∆的符号，从而判断出实根的情况．若在区间),(n m 内研究二次方程02=++c bx ax ，则需由二次函数图象与区间关系来确定．分布情况 两根都小于k 即 k x k x <<21, 两根都大于k 即 k x k x >>21, 一个根小于k ，一个大于k 即 21x k x <<大致图象（0>a ）得出的结论()020b k a f k ∆>⎧⎪⎪-<⎨⎪>⎪⎩ ()020b k a f k ∆>⎧⎪⎪->⎨⎪>⎪⎩ ()0<k f分布情况两根都在()n m ,内 两根有且仅有一根在()n m ,内 （图象有两种情况，只画了一种） 一根在()n m ,内，另一根在()q p ,内，q p n m <<<kk k大致图象（>a ）得出的结论 ()()0002f m f n b m n a ∆>⎧⎪>⎪⎪>⎨⎪⎪<-<⎪⎩ ()()0<⋅n f m f ()()()()0000f m f n f p f q ⎧>⎪<⎪⎨<⎪⎪>⎩或()()()()00f m f n f p f q <⎧⎪⎨<⎪⎩ 根在区间上的分布还有一种情况：两根分别在区间()n m ,外，即在区间两侧12,x m x n <>，（图形分别如下）需满足的条件是 （1）0a >时，()()00f m f n <⎧⎪⎨<⎪⎩； （2）0a <时，()()00f m f n >⎧⎪⎨>⎪⎩ 对以上的根的分布表中一些特殊情况作说明： （1）两根有且仅有一根在()n m ,内有以下特殊情况：1︒ 若()0f m =或()0f n =，则此时()()0f m f n <不成立，但对于这种情况是知道了方程有一根为m 或n ，可以求出另外一根，然后可以根据另一根在区间()n m ,内，从而可以求出参数的值。

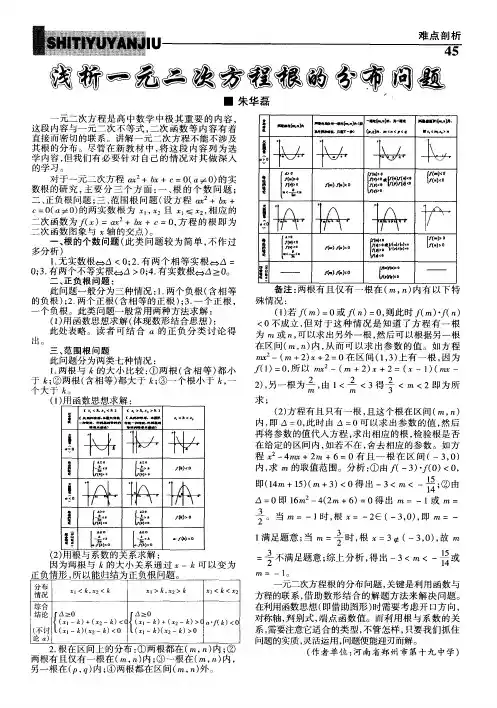
实系数一元二次方程实根分布1：当m 为何值时，方程03524222=--++m m mx x的两根异号？答案：(321<<-m )2：已知方程02322=-+-k kx x 的两个根都大于1，求k 的取值范围。

答案：(2≥k )3：已知集合A ＝｛045|2≤+-x x x ｝，B ＝｛022|2≤++-a ax x x ｝，且B ⊆A ，求实数a 的取值范围。

答案：(7181≤<-a )4、关于x 的方程0122=++x ax 至少有一个负的实根，则a_____________ (1≤a )5、01032=+-k x x 有两个同号且不相等的实根,则k__________- (3250<<k )6、要使关于x 的方程0322=+-kx x 的两个实根一个小于1，另一个大于1，则实数k 的取值范围是__（ 5>k ）7、已知抛物线m x m x y +-+=)3(2与x 轴的正半轴交于两点，则实数m 的取值范围是＿＿＿＿。

（10<<m ）8、设A ＝｛01|2=-x x ｝，B ＝｛012|22=-+-a ax x x ｝，若A ∩B ＝B ，则a 等于＿＿＿。

(0=a )9、已知A ＝｛01)2(|2=+++x p x x ，R x ∈｝，若A ∩R ＋＝φ，则p 的范围是＿＿＿＿＿。

(4->p )10、已知方程0222=++-a ax x 的两根都在区间（1,4）内， 求a 的取值范围。

(7182<≤a )11、若关于x 的方程0532=+-a x x 的一个根在（－2,0）内，另一个根在（1,3）内，求a 的取值范围。

12、已知方程01222=+-+m mx x 的两个实根都大于2,求实数m 的取值范围。

（4316-≤<-m ）13已知A ＝｛023|2≤+-x x x ｝，B ＝｛02|2≤+-a ax x x ，R a ∈｝，且A ∩B ＝B ，求a 的取值范围。

一元二次方程的形式为ax^2+bx+c=0，其中a、b、c为常数。

一元二次方程根的分布取决于方程的解的个数，有如下三种情况：1 两个不相等的实根：如果一元二次方程有两个不相等的实根，那么方程的解为x1=r1、x2=r2，其中r1和r2是方程的两个实根。

2 两个相等的实根：如果一元二次方程有两个相等的实根，那么方程的解为x1=x2=r，其中r是方程的两个相等的实根。

3 两个复数根：如果一元二次方程有两个复数根，那么方程的解为x1=r1+r2i、x2=r1-r2i，其中r1和r2是方程的两个复数根的实部和虚部。

一元二次方程的根分布可以通过求解方程的判别式来确定。

判别式为b^2-4ac，如果判别式>0，则方程有两个不相等的实根；如果判别式=0，则方程有两个相等的实根；如果判别式<0，则方程有两个复数根。

在数学中，一元二次方程是由一个二次项和一个一次项组成的方程。

它的形式为ax^2+bx+c=0，其中a、b、c为常数。

解决一元二次方程的方法有多种，常见的方法有求解公式法、因式分解法、二分法、牛顿迭代法等。

求解公式法是最常见的求解一元二次方程的方法，它的公式为：x1= (-b+sqrt(b^2-4ac))/(2a)x2= (-b-sqrt(b^2-4ac))/(2a)其中sqrt(b^2-4ac)表示根号内的值。

因式分解法是将一元二次方程写成两个一次方程的形式，然后分别求解两个一次方程的解。

二分法是一种数值解法，通过取方程的两个端点的中点来逐步缩小解的范围，最终得到方程的解。

牛顿迭代法是一种逐步迭代的方法，通过不断迭代来逼近方程的解，最终得到方程的解。

在解决一元二次方程时，应根据具体情况选择合适的方法。

专题二、一元二次方程的实根分布问题
问题: 已知方程0)3(2=+-+m x m x ，求实数m 的取值范围。

条件1：若方程有两个正根。

条件2：若方程的两个根均小于1。

条件3：若方程的一个根大于1，一个根小于1。

条件4：若方程的两个根均在( 0，2)内。

条件5：若方程的两个根有且仅有一个在( 0，2)内。

条件6：若方程的一个根在(–2 ，0)，另一个根在(0 ，4)。

条件7：若方程的一个根小于2，另一个根大于4。

条件8：若方程有一个正根，一个负根且正根的绝对值较大。

1.若方程02)13(22=--++-m m x m x 在区间(0，1)、(1，2)上各有一个实根，求实数m 的取值范围。

2.若方程02)2(22=----m m x m x 的两根在区间[0，1]之外两旁，求实数m 的取值范围。

3.关于x 的方程023222=---k x kx 的二根，一个小于1，另一个大于1，则
求实数k 的取值范围。

4.若方程0122=-+-m mx x 在区间(–2，4)上有两根，求实数m 的取值范围。

一元二次方程的根的分布问题 一、定理： 设：f (x )=ax 2+bx +c （a ＞0），△=b 2－4ac定理1 方程f (x )=0的两实根都大于（或小于）给定的实数m 的充要条件是 定理2 方程f (x)=0的两实根在区间（m ，n ）的充要条件是 定理3 方程f (x)=0的两实根分别在区间（p ，q ）与（q ，r ）内的充要条件是⎪⎩⎪⎨⎧><>0)(0)(0)(r f q f p f定理4 方程f (x)=0的两实根分别在区间（p ，q ）与（r ，s ）（r ≥q ）的充要条件是⎪⎪⎩⎪⎪⎨⎧><<>0)(0)(0)(0)(s f r f q f p f 定理5 方程f (x)=0的两实根中一根小于m ，另一根大于n （m ＜n ）的充要条件是 定理6 方程f (x)=0的两实根x 1、x 2满足x 1＜m ＜x 2的充要条件是x y o m －a b 2 －a b2 x y o mxyo －a b 2 m n p q rp q r s xy o m n m x 1 x 2小结：⑴若两实根分布在同一开区间．．．（m ，n ），则必须考虑三点：①判别式△≥0；②对称轴在所给区间内，即m ＜a b2 ＜n ；③在区间端点处函数值的符号，即f (m)＞0且f (n)＞0.⑵若两实根分布在两个不同的开区间．．．内，则只要考虑在区间端点处函数值的符号.二、例题：例1、若方程（k 2+1）x 2－2（k+1）x+1=0的两根在区间（0，1）内，求k 的取值范围.例2、求实数m ，使方程7x 2－（m+13）x+m 2－m －2=0有两实根，且它们分别在区间（0，1）与（1，2）中.例3、方程x 2+（a 2－1）x+a －2=0有一根大于1，另一根小于－1，求a 的取值范围.例4、若方程x 2－11x+m=0的两根都大于5，求m 的取值范围.例5、若方程x 2 l ga －2x+1=0的一根大于1，另一根小于1，求实数a 的取值范围.例6、若a ＞b ＞0，证明方程0112=+-+-b x a x ，有两相异实根，且一根在（b ，a ）之间，另一根比b 小.练习题1、 已知方程x 2－2x+ l g （2a 2－a ）=0有一正根和一负根，求实数a 的取值范围.2、求使方程x 2－2mx+m+1=0有两实根，且一根大于5，一根小于5的实数m 的取值范围.3、方程x 2+2（k+3）x+2k+4=0有两个相异实根， ⑴若一根大于3，另一根小于1，求k 的取值范围； ⑵若两根都在区间（－2，2）内，求k 的取值范围； ⑶若方程有且只有一个实根在（1，2）内，另一根不在其内，求k 的取值范围.4、设a 是任意实数，二次方程3x 2－1=a （2x －1）有两个不等的实根，证明两根中至少有一个在区间（0，1）之间.。

一元二次方程实根的分布一元二次方程实根的分布是二次方程中的重要内容，在各类竞赛和中考中经常出现。

这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于一元二次方程根的判别式和根与系数关系（韦达定理）的运用。

本文将在前面方法的基础上，结合二次函数图象的性质，分两种情况系统地介绍一元二次方程实根分布的情况及其运用。

一．一元二次方程实根的基本分布——零分布一元二次方程实根的零分布，指的是方程的根相对于零的关系。

比如二次方程有一正根，有一负根，其实就是指这个二次方程一个根比零大，一个根比零小，或者说，这两个根分布在零的两侧。

对于这类问题，用一元二次方程根的判别式和根与系数关系（韦达定理）即可判别。

一元二次方程02=++c bx ax （0≠a ）的两个实数根为1x 、2x ，则1x 、2x 均为正⇔△≥0，1x ＋2x ＞0，1x 2x ＞0； 1x 、2x 均为负⇔△≥0，1x ＋2x ＜0，1x 2x ＞0；1x 、2x 一正一负⇔1x 2x ＜0。

例1．关于x 的一元二次方程28(1)70x m x m +++-=有两个负数根，求实数m 取值范围。

解：设两个实数根为1x 、2x ，依题意有1212000x x x x ∆⎧⎪+< ⎨⎪> ⎩≥ ①②③由①得：2(1)32(7)0m m +--≥，2(15)0m -≥，恒成立。

由②得：18m +-＜0，解之，m ＞1-。

由③得：78m -＞0，解之，m ＞7。

综上，m 的取值范围是m ＞7。

例2．若n ＞0，关于x 的方程21(2)04x m n x mn --+=有两个相等的正实数根，求mn 的值。

解：设两个实数根为1x 、2x ，依题意有1212000x x x x ∆= ⎧⎪+⎨⎪> ⎩①＞ ②③由①得：2(2)0m n mn --=，()(4)0m n m n --=，∴m n =或4m n =。

若m n =，则1x ＋2x 22m n n n n =-=-=-＜0，不符合②，舍去。

一元二次方程的实根分布问题引言一元二次方程是高中数学中重要的内容之一，也是解决实际问题中常见的一种数学模型。

解一元二次方程可以得到方程的实根，实根的个数和分布与方程的系数有密切关系。

本文将探讨一元二次方程的实根分布问题，并给出相应的和解题方法。

一元二次方程的一般形式一元二次方程的一般形式为：ax2+bx+c=0，其中a、b和c分别为方程的系数，且a eq0。

实根、虚根和重根一个一元二次方程可能有三种情况：实根、虚根和重根。

- 当判别式D=b2−4ac大于 0 时，方程有两个不相等的实根； - 当判别式小于 0 时，方程没有实根，但有两个虚根； - 当判别式等于 0 时，方程有两个相等的实根（重根）。

实根分布问题实根分布问题即研究实根的个数和分布。

首先，我们考虑a>0的情况。

1. 当a>0时对于一元二次方程ax2+bx+c=0，当a>0时，判别式D=b2−4ac的符号关系决定了实根的个数和分布。

a) 当D>0时当判别式D=b2−4ac>0时，方程有两个不相等的实根。

实根的分布取决于方程的系数a、b和c。

根据配方法，我们可以将一元二次方程写成完全平方形式(x−p)2=q，其中p和q可以通过系数a、b和c表示出来。

b) 当D<0时当判别式D=b2−4ac<0时，方程没有实根，但有两个虚根。

c) 当D=0时当判别式D=b2−4ac=0时，方程有两个相等的实根（重根）。

2. 当a<0时对于一元二次方程ax2+bx+c=0，当a<0时，判别式D=b2−4ac的符号关系同样决定了实根的个数和分布。

a) 当D>0时当判别式D=b2−4ac>0时，方程有两个不相等的实根。

b) 当D<0时当判别式D=b2−4ac<0时，方程没有实根，但有两个虚根。

c) 当D=0时当判别式D=b2−4ac=0时，方程有两个相等的实根（重根）。

根据以上讨论，我们可以出一元二次方程的实根分布问题的： 1. 当判别式D= b2−4ac>0时，方程有两个不相等的实根； 2. 当判别式D=b2−4ac<0时，方程没有实根，但有两个虚根； 3. 当判别式D=b2−4ac=0时，方程有两个相等的实根（重根）。

处理一元二次方程实根分布情况下求参问题的4个方法一元二次方程是形如ax²+bx+c=0的方程，其中a、b、c是已知常数，而x是未知数。

求解一元二次方程的根是数学中常见的问题，但是有时候方程的根的分布情况会对求参问题提出了一定的要求。

本文将介绍求解一元二次方程实根分布情况下的四种方法。

方法一：直接求解法直接求解法是最常见也是最简单的一种方法。

根据一元二次方程的求根公式x=(-b±√(b²-4ac))/2a，我们可以根据方程的系数a、b、c来求出方程的根。

此方法适用于一元二次方程只有一个根或两个重根的情况。

方法二：判别式法判别式法是针对不同根的情况进行求解的一种方法。

方程的判别式D=b²-4ac可以提供方程的根的情况。

1.当D>0时，方程有两个不相等的实根。

2.当D=0时，方程有两个相等的实根，即重根。

3.当D<0时，方程没有实根，而有两个虚根。

方法三：解曲线与直线的交点法解曲线与直线的交点法是一种几何方法。

根据一元二次方程的几何意义，我们可以绘制出方程的二次曲线和与其相交的直线。

通过观察交点的数量和位置，我们可以得到方程实根的情况。

当曲线和直线相交于两点时，方程有两个不相等的实根；当曲线和直线相切于一点时，方程有一个实根；当曲线和直线没有交点时，方程没有实根。

方法四：代数方法代数方法是一种基于代数运算的求解方法。

通过对方程进行变形、化简、整理等代数运算，我们可以得到方程的根的一些特征。

例如，通过配方法将一元二次方程转化为一个完全平方后，我们可以得到它的根（不一定是实根）；通过因式分解将一元二次方程分解为两个一次因式的乘积后，我们可以得到方程的根的数量和特征。

这四种方法可以根据实际情况的不同进行选择和组合使用。

其中，直接求解法适用于一元二次方程只有一个根或两个重根的情况；判别式法适用于判定方程的根的情况；解曲线与直线的交点法适用于通过图像观察根的情况；代数方法适用于通过代数运算得到根的特征的情况。

第一课时：一元二次方程实数根的分布教学目标：使学生掌握一元二次方程实根分布问题的处理，加强求解一元二次不等式及不等式组，初步训练学生的数形结合能力。

教学重点：利用二次函数的图象，把一元二次方程根的分布−−→−转化图形问题−−→−转化代数表达式（不等式组）−−→−计算参数取值范围。

教学难点：图形问题转化成代数表达式(不等式组)并求解。

一、问题的提出若方程0)5()2(2=++++m x m x 的两根均为正数，求实数m 的取值范围.变式1：两根一正一负时情况怎样？变式2：两实根均大于5时情况又怎样？变式3：一根大于2，另一根小于-1时情况又怎样？问题：能否从二次函数图形角度去观察理解？若能试比较两种方法的优劣.方程)0(02≠=++a c bx ax 的实根，如若从二次函数图形角度去观察理解，其实质就是对应的二次函数2()0(0)f x ax bx c a =++=≠ 的抛物线与x 轴交点的横坐标.一元二次方程实根分布，实质上就是方程的根与某些确定的常数大小关系比较.二、一元二次方程实根分布仿上完成下表一元二次方程)0(02≠=++a c bx ax 实根分布图解三、练习1.m 为何实数时，方程02)1(2=+++m x m x 的两根都在-1与1之间.2、若方程0)3()1(2=-++-a x a x 的两根中，一根小于0，另一根大于2，求a 的取值范围.四、小结基本类型与相应方法：设 )0()(2≠++=a c bx ax x f ，则方程0)(=x f 的实根分布的基本类型及相应方法如下表：五作业：1．关于x 的一元二次方程222320ax x a ---=的一根大于1，另一根小于1.则a 的值是 （ ）（A ）0a >或4a <- （B ）4a <- （C ）0a > （D ）40a -<<2．方程227(13)20(x k x k k k -++--=为常数）有两实根,αβ，且01α<<，12β<<，那么k 的取值范围是 （ ）（A ）34k << （B ）21k -<<- （C ）21a -<<-或34k << （D ）无解3．设m 是整数，且方程2320x mx +-=的两根都大于95-而小于37，则m = .4.若关于x 的方程22(1)210m x mx -+-=的所有根都是比1小的正实数，则实数m 的取值范围是m ＝5. 方程2(21)(6)0x m x m +-+-=的一根不大于－1，另一根不小于1.试求：（1）参数m 的取值范围；（2）方程两根的平方和的最大值和最小值. 第二课时 一元二次方程实数根分布的应用一复习二、例子例1 已知实数a 、b 、c 满足22211a b c a b c a b c ⎧>>⎪++=⎨⎪++=⎩，求a b +的取值范围.解 由已知得1a b c +=-且222222()()(1)(1)22a b a b c c ab c c +-+---===-.所以,a b 是一元二次方程22(1)()0x c x c c --+-=的两根. 由a b c>>问题可转化为方程22(1)()0x c x c c --+-=的二根都大于c .令()f x =22(1)()x c x c c --+-，有2212()0(1)4()0c cf c c c c -⎧>⎪⎪>⎨⎪∆=--->⎪⎩ 即22123203210c c c c c c ->⎧⎪->⎨⎪--<⎩， 求得103c -<<，因此4(1,)3a b +∈.例2已知点(0,4)A 、(4,0)B .若抛物线21y x mx m =-++与线段AB (不包括端点A 及B )有两个不同的交点，则m 的取值范围是 . (1997年上海市高中数学竞赛)解： 显然直线AB 的方程为1(04)44x y x +=<<即4y x =-，代入抛物线方程并整理得2(1)(3)0x m x m +-+-=.设2()(1)(3)f x x m x m =+-+-，问题转化函数()y f x =的图象和x 轴在0到4之间有两个不同的交点，即方程2(1)(3)0x m x m +-+-=在(0,4)上有两个不相等的实根. 所以2(1)4(3)0(0)30(4)164(1)30104.2m m f m f m m m ⎧∆=--->⎪=->⎪⎪⎨=--+->⎪-⎪<<⎪⎩ 解得m 的取值范围是1733m <<. 例3关于x 的实系数二次方程20x ax b ++=的两个实数根为,αβ，证明：①如果||2,||2αβ<<，那么2||4a b <+且||4b <；②如果 2||4a b <+且||4b <，那么||2,||2αβ<<.(1993年全国高考题)证明 ①设2()f x x ax b =++，由已知，函数()y f x =的图象与x 轴在2-到2之间有两个不同的交点. 所以240,(1)22,(2)2(2)420,(3)(2)420.(4)a b a f a b f a b ⎧∆=->⎪⎪-<-<⎪⎨⎪-=-+>⎪=++>⎪⎩由(3)、(4)得(4)24b a b -+<<+，所以2||4a b <+.由(2)，得||4a <，结合(1)得2416b a <<，所以4b <. 将(3)+(4)得4b >-，因此44b -<<，即||4b <.②由于2||4a b <+且||4b <，可得4,2||448b a <<+=，所以||4a <，222a -<-<. 即函数()f x 的图象的对称轴2a x =-位于两条直线2x =-，2x =之间.因为(2)(2)(42)(42)2(4)0f f a b a b b -+=+++-+=+>，22(2)(2)(42)(42)(4)40f f a b a b b a -⋅=++-+=+-> .所以(2)0,(2)0f f ->>. 因此函数()f x 的图象与x 轴的交点位于-2和2之间，即||2,||2αβ<<.作业1．已知抛物线2(4)2(6),y x m x m m =++-+为实数.m 为何值时，抛物线与x 轴的两个交点都位于点(1,0)的右侧？2．已知,,a b c 都是正整数，且抛物线2()f x ax bx c =++与x 轴有两个不同的交点A 、B. 若A 、B 到原点的距离都小于1，求a b c ++的最小值.第三课时 应用提高例1若方程k x x =-232在[]1,1-上有实根，求实数k 的取值范围. 解法一：方程k x x =-232在[]1,1-上有实根，即方程0232=--k x x 在[]1,1-上有实根，设k x x x f --=23)(2，则根据函数)(x f y =的图象与x 轴的交点的横坐标等价于方程0)(=x f 的根. （1）两个实根都在[]1,1-上，如图：可得⎪⎪⎩⎪⎪⎨⎧≤-≤-≥≥-≥∆1210)1(0)1(0a b f f ，解得2169-≤≤-k ； （2）只有一个实根在[]1,1-上，如图：可得0)1()1(≤⋅-f f ，解得 2521≤≤-k ，综合（1）与（2）可得 实数k 的取值范围为⎥⎦⎤⎢⎣⎡-25,169 解法二：方程k x x =-232在[]1,1-上有实根，即存在[]1,1-∈x ，使得等式x x k 232-=成立，要求k 的取值范围，也即要求函数[]1,1,232-∈-=x x x k 的值域. 设[]1,1,1694323)(22-∈-⎪⎭⎫ ⎝⎛-=-==x x x x x f k 又因，则)1(169-≤≤-f k ， 可得25169≤≤-k . 解法三：令,232x x y -=则k y =，则方程k x x =-232在[]1,1-上有实根，等价于方程组⎪⎩⎪⎨⎧=-=k y x x y 232在[]1,1-上有实数解，也即等价于抛物线,232x x y -=与直线k y =在[]1,1-上有公共点，如图所示直观可得：25169≤≤-k .解法四：根据解法三的转化思想，也可将原方 程k x x =-232化成k x x +=232，然后令 k x y x y +==23,2，从而将原问题等价转化为 抛物线2x y =与直线k x y +=23在[]1,1-点时，“数形结合法”下去求参数k 的取值范围.根据图形直观可得：当直线k x y +=23过点)1,1(-， 截距k 最大；当直线k x y +=23与抛物线k x y +=23相切时，截距k 最小. 且169,25-==最小最大k k .故参数的取值范围为25169≤≤-k . 2已知实数a 、b 、c 满足021a b c m m m++=++，其中m 为正数.对于2()f x ax bx c =++. (1)若0a ≠，求证：()01m af m <+； (2) 若0a ≠，证明方程()0f x =在(0,1)内有实根.证明 (1)由021a b c m m m ++=++，求得()21am bm c m m =-+++，所以 222222211()[()()][()][]11112(1)2m m m m m af a a b c a a m m m m m m m m m=++=-=-+++++++ 又由22(1)20m m m +>+>，因此22110(1)2m m m -<++，故()01m af m <+. (2)要证明方程()0f x =在(0,1)内有实根，只须证明(0)(1)0f f ⋅< 或 (0)0,(1)0,0,0 1.2af af b a >⎧⎪>⎪⎪∆≥⎨⎪⎪<-<⎪⎩但两者都不易证明. 由01(0)1m m m <<>+，结合第(1)题()01m af m <+，对a 进行讨论： 当0a >时，有()01m f m <+. 只要证明(0)f c =和(1)f a b c =++中有一个大于零即可. 若0c >，则(0)0f >成立，问题得证；若0c ≤，由021a b c m m m ++=++求得(1)(1)2a m c m b m m++=--+，所以 (1)(1)(1)22a m c m a c f a b c a c m m m m ++=++=--+=-++. 由0,0,0a m c >>≤，知(1)0f >，命题得证. 故当0a >时，方程()0f x =在(0,1)内有实根. 同理可证，当0a <时，方程()0f x =在(0,1)内也有根.。