六年级一元一次不等式50

一元一次不等式组50题一．解答题（共50小题）1．解不等式（组），并把它们的解集在数轴上表示出来：①4x+1≤3x+3②2．（1）解不等式3（x﹣2）＞2（7﹣x），并把它的解集表示在数轴上．（2）．3．解方程组或不等式组：（1）解方程组．（2）解不等式组，并把解集在数轴上表示出来．4．（1）已知，（x﹣1）3＝8，求x的值；（2）解不等式组并把不等式组解集在数轴上表示出来．5．解不等式组，并将不等式组的解集在数轴上表示出来．6．解不等式组：并在数轴上表示其解集．7．（1）解不等式2（x+1）﹣，并把它的解集在数轴上表示出来；（2）解不等式组：．8．已知关于x、y的方程组（1）若是方程组的解时，求3m+n的值；（2）当n＝﹣2时，若方程组的解满足x为非正数，y为负数，化简：|m﹣3|﹣|m+2|．9．（1）计算：．（2）解不等式组：，并把它的解集在数轴上表示出来．10．已知方程组．（1）求方程组的解（用含有a的代数式表示）；（2）若方程组的解x为负数，y为非正数，且a+b＝4，求b的取值范围．11．解方程组及不等式组（1）；（2）．12．解不等式组，并把解集在数轴上表示出来．（1）；（2）．13．解不等式组：．14．解下列不等式或不等式组，并把解集在数轴上表示出来．（1）；（2）15．解下列不等式（组），并把它们的解集在数轴上表示出来：（1）5x≥2x+6；（2）．16．解下列不等式（组）：（1）﹣4＞﹣；（2）解不等式组．17．解不等式组：18．解不等式组19．解下列不等式组，并把它的解集在数轴上表示出来；20．解下列方程组（不等式组）（1）；（2）．21．解不等式组：，并把不等式组的解集在数轴上表示出来．22．（1）计算：﹣2﹣1+（﹣π）0﹣|﹣2|﹣2sin60°；（2）解不等式组：．23．（1）计算：4cos30°+（1﹣）0﹣+（）﹣1；（2）解不等式组．24．解不等式组：25．计算：（1）﹣14﹣（1﹣0.5）××[2﹣（﹣3）2]；（2）解不等式组，并把解集在数轴上表示出来．26．（1）计算：|﹣2﹣2sin45°|+（2﹣π）0﹣（）﹣2（2）解不等式组并在数轴上表示它的解集．27．解不等式组，并把解集在数轴上表示出来：28．解不等式组，并把它们的解在数轴上表示出来．29．解下列不等式（组）（1）2x﹣1＞x﹣3（2）30．解不等式组：．31．解不等式组：32．解不等式组33．解不等式组：34．解不等式组：，并把解集表示在数轴上．35．解不等式组：36．已知方程组的解x、y都是正数，且x的值小于y的值，求m的取值范围．37．解不等式组．，把不等式组的解集在数轴上表示出来．38．解不等式组并把它的解集在数轴上表示出来．39．解不等式组：，并将解集在数轴上表示出来．40．解不等式组：，并把它的解集在数轴上表示出来．41．解不等式组：，并把解集在数轴上表示出来．42．解不等式组．43．解不等式组：，并将它的解集在数轴上表示出来．44．解不等式组，并把解集在数轴上表示出来．45．解不等式组：，并把解集在数轴上表示出来．46．解不等式组：．47．解不等式组，并把解集在数轴上表示出来．48．解不等式组：，并将解集在数轴上表示出来．49．解不等式组请结合题意填空，完成本题的解答：（Ⅰ）解不等式①，得；（Ⅱ）解不等式②，得；（Ⅲ）把不等式①和②的解集在数轴上表示出来；（Ⅳ）原不等式组的解集为．50．解不等式组请结合题意填空，完成本题的解答．（Ⅰ）解不等式①，得；（Ⅱ）解不等式②，得；（Ⅲ）把不等式①和②的解集在数轴上表示出来：（Ⅳ）原不等式组的解集为．一元一次不等式组二一．解答题（共50小题）1．解不等式组，并把它的解集表示在数轴上．2．解不等式组：，并把解集表示在数轴上．3．解不等式组，并把解集表示在数轴上．4．解不等式组并把它的解集在数轴上表示出来．5．解不等式组：并在数轴上表示它的解集．6．解不等式组并写出它的正整数解．7．解不等式组：，并写出该不等式组的整数解．8．解不等式组：，并把其解集在数轴表示出来．9．解不等式组，并将解集在数轴上表示出来．10．解不等式组，并把解集在数轴上表示出来．（1）（2）11．解不等式（组）（1）解不等式：（x+2）（x﹣5）﹣（x﹣1）2≥﹣3．（2）解不等式组：，并将解集表示在数轴上．12．解不等式（组）：（1）19﹣3（x+7）≤0（2）13．解下列不等式组和方程组（1）；（2）．14．解下列不等式（组）．（1）5x﹣3＜1﹣3x；（2）15．解不等式组，并在数轴上画出解集．16．解方程组和不等式组（1）解方程组．（2）解不等式组，并把解集表示在数轴上．17．已知关于x、y的方程组的解都为正数．（1）求a的取值范围；（2）已知a+b＝4，且b＞0，z＝2a﹣3b，求z的取值范围．18．解不等式（组），并把解集在数轴上表示出来．（1）（2）．19．已知方程组的解满足x为非正数，y为负数．（1）求m的取值范围；（2）化简：|m﹣3|﹣|m+2|．20．已知方程组中x为非正数，y为负数．（1）求a的取值范围；（2）在a的取值范围中，当a为何整数时，不等式2ax+x＞2a+1的解集为x＜1．21．解不等式组：．把它的解集在数轴上表示出来，并写出这个不等式组的整数解．22．解不等式组．23．解不等式组，并把解集在数轴上表示出来．24．已知关于x、y的二元一次方程组的解满足不等式组，则m的取值范围是什么？25．解不等式组：（注：必须通过画数轴求解集）26．解不等式组．27．解不等式组：，并把解集在数轴上表示出来．28．请从不等式﹣4x＞2，，中任选两个组成一个一元一次不等式组．解出这个不等式组，并在数轴上表示出它的解集．29．已知不等式组的解集为﹣1＜x＜1，求（a+1）（b﹣1）的值．30．若不等式组的解集为﹣1≤x≤2，（1）求a、b的值（2）解不等式ax+b＜0，并把它的解集在下面的数轴上表示出来．31．解不等式组，并把解集在数轴上表示出来．（1）（2）32．解下列不等式（组），并把它们的解集在数轴上表示出来：①3x﹣8＜5x②33．解不等式组：．34．解不等式组35．已知关于a的不等式组．（1）求此不等式组的解；（2）试比较a﹣3与的大小．36．解不等式组，并将解集在数轴上表示出来．37．解不等式组：，并把解集表示在数轴上．38．解不等式组：，并把它的解集在数轴上表示出来．39．解不等式组．40．解不等式组，并把它的解集在数轴上表示．41．解不等式组：，并把它的解集在数轴上表示出来．42．已知关于x，y的方程组满足﹣2＜x﹣y＜1，求m的取值范围．43．解不等式组：44．解一元一次不等式组．45．若不等式组：的解集是5＜x＜22，求a，b的值．46．解不等式，并在数轴上把它的解集表示出来．47．已知关于x，y的方程组的解为正数，求m的取值范围．48．解不等式和不等式组．（1）．（2）．49．解不等式（组）（1）（2）．50．解不等式组并将解集在数轴上表示出来．。

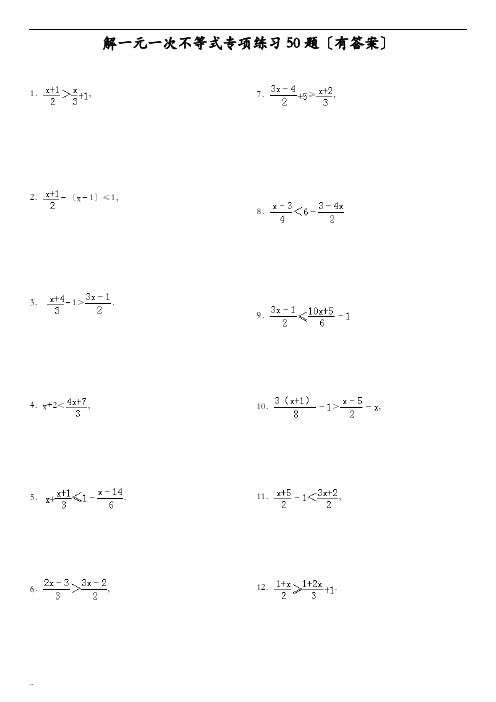
解一元一次不等式专项练习50题〔有答案〕1．，2．﹣〔x﹣1〕≤1，3．﹣1＞．4．x+2＜，5．．6．，7．≥，8．9．10．＞，11．，12．．13．，14. 3x ﹣，15．3〔x﹣1〕+2≥2〔x﹣3〕．16．，17．10﹣4〔x﹣4〕≤2〔x﹣1〕，18．﹣1＜．19．．20．≤．21．，22．，23．≥．24．＞1．25．．26．，27．≥，28．；29.．30．≤31．，32．〔x+1〕≤2﹣x 33．2〔5x+3〕≤x﹣3〔1﹣2x〕34．≤+1．35．；36.．37．．38．4x+3≥3x+5．40．＞x﹣141．2〔3﹣x〕＜x﹣3．42．3〔x+2〕≤5〔x﹣1〕+7，43．1﹣≥44．2〔x+3〕﹣4x＞3﹣x．45．2〔1﹣2x〕+5≤3〔2﹣x〕46．，47．．48．2﹣＞3+．49．4〔x+3〕﹣＜2〔2﹣x〕﹣〔x ﹣〕50．．解不等式50题参考答案：1．解：去分母得：3〔x+1〕＞2x+6，去括号得：3x+3＞2x+6，移项、合并同类项得：x＞3，∴不等式的解集为x＞32．解：去分母得：x+1﹣2〔x﹣1〕≤2，∴x+1﹣2x+2≤2，3．解：去分母得2〔x+4〕﹣6＞3〔3x﹣1〕，去括号得2x+8﹣6＞9x﹣3，移项得2x﹣9x＞﹣3﹣8+6，合并同类项得﹣7x＞﹣5，化系数为1得x ＜移项、合并同类项得：﹣x＜1，不等式的两边都除以﹣1得：x＞﹣1，∴不等式的解集是x＞﹣15．解：去分母，得6x+2〔x+1〕≤6﹣〔x﹣14〕去括号，得6x+2x+2≤6﹣x+14…〔3分〕移项，合并同类项，得9x≤18 …〔5分〕两边都除以9，得x≤26．解：去分母得：2〔2x﹣3〕＞3〔3x﹣2〕去括号得：4x﹣6＞9x﹣6移项合并同类项得：﹣5x＞0∴x＜07．解：去分母得，3〔3x﹣4〕+30≥2〔x+2〕，去括号得，9x﹣12+30≥2x+4，移项，合并同类项得，7x≥﹣14，系数化为1得，x＞﹣28．解：x﹣3＜24﹣2〔3﹣4x〕，x﹣3＜24﹣6+8x，x﹣8x＜24﹣6+3，﹣7x＜21，x＞﹣39．解：化简原不等式可得：6〔3x﹣1〕≤〔10x+5〕﹣6，即8x≥﹣16，可求得x≥﹣210．解：去分母，得3〔x+1〕﹣8＞4〔x﹣5〕﹣8x，去括号，得3x+3﹣8＞4x﹣20﹣8x，移项、合并同类项，得7x＞﹣15，系数化为1，得x ＞﹣11．解：去分母，得x+5﹣2＜3x+2，移项，得x﹣3x＜2+2﹣5，合并同类项，得﹣2x＜﹣1，化系数为1，得x ＞12．解：去分母，得3〔x+1〕≥2〔2x+1〕+6，去括号，得3x+3≥4x+2+6，移项、合并同类项，得﹣x≥5，系数化为1，得x≤﹣513．解：去分母，得2〔2x﹣1〕﹣24＞﹣3〔x+4〕，去括号，得4x﹣2﹣24＞﹣3x﹣12，移项、合并同类项，得7x＞14，两边都除以7，得x＞214．解：去分母得，6x﹣1＜2x+7，移项得，6x﹣2x＜7+1，合并同类项得，4x＜8，化系数为1得，x＜215．解：3〔x﹣1〕+2≥2〔x﹣3〕，解得：x≥﹣516．解：去分母得：2〔x﹣1〕﹣3〔x+4〕＞﹣12，去括号得：2x﹣2﹣3x﹣12＞﹣12，移项得：2x﹣3x＞﹣12+2+12，合并得：﹣x＞2，解得：x＜﹣217．解：去括号得：10﹣4x+16≤2x﹣2，移项合并得：﹣6x≤﹣28，解得：x≥18．解：去分母得，3〔x+5〕﹣6＜2〔3x+2〕，去括号得，3x+15﹣6＜6x+4，移项、合并同类项得，5＜3x，把x的系数化为1得x ＞．19．解：∵∴3〔x+5〕﹣6＜2〔3x+2〕∴3x+15﹣6＜6x+4∴3x﹣6x＜4﹣15+6∴﹣3x＜﹣5∴x20．解：去分母得30﹣2〔2﹣3x〕≤5〔1+x〕，去括号得30﹣4+6x≤5+5x，移项得6x﹣5x≤5+4﹣30，合并得x≤﹣2121．解：去分母得，2〔2x﹣1〕﹣6x＜3x+3，去括号得，4x﹣2﹣6x＜3x+3，移项得，4x﹣6x﹣3x＜3+2，合并同类项得，﹣5x＜5，系数化为1得，x＞﹣1．故此不等式的解集为：x＞﹣122．解：去分母得，2〔2x﹣5〕＞3〔3x+4〕+18，去括号得，4x﹣10＞9x+12+18，移项得，4x﹣9x＞12+18+10，合并同类项得，﹣5x＞40，系数化为1得，x＜﹣823．解：≥1﹣，去分母得：2〔2x﹣1〕≥6﹣3〔5﹣x〕，去括号得：4x﹣2≥6﹣15+3x，移项合并得：x≥﹣724．解：原不等式可变为：2〔x+4〕﹣3〔3x﹣1〕＞6，2x+8﹣9x+3＞6，﹣7x＞﹣5，25．解：原不等式可化为，6〔2x﹣1〕≥10x+1，去分母得，12x﹣6≥10x+1，合并同类项得，2x≥7，把系数化为1得，x≥26．解：去分母得，2〔2x﹣1〕﹣6≤3〔5x﹣1〕，去括号得，4x﹣2﹣6≤15x﹣3，移项得，4x﹣15x≤﹣3+2+6，合并同类项得，﹣11x≤5，化系数为1得，x≥﹣27．解：去分母，得32﹣2〔3x﹣1〕≥5〔x+3〕+8；去括号，得32﹣6x+2≥5x+15+8；移项，得﹣6x﹣5x≥15+8﹣32﹣2；合并同类项，得﹣11x≥﹣11；系数化为1，得x≤128．解：〔1〕在不等式的左右两边同乘以2得，〔3﹣x〕﹣6≥0，解得：x≤﹣3，29. 〔2〕在不等式的左右两边同乘以12得，6〔2x﹣1〕﹣4〔2x+5〕＜3〔6x﹣7〕，解得：x30．解：不等式两边都乘以8得，32﹣2〔3x﹣1〕≤5〔x+3〕+8，去括号得，32﹣6x+2≤5x+15+8，移项得，11≤6x+5x，∴x≥131．解：∵，∴12x﹣6﹣8x﹣20＜18x﹣21﹣12，∴14x＞7，∴32．解：不等式两边同时乘以2，得：x+1≤4﹣2x，移项，得：x+2x≤4﹣1，合并同类项，得：3x≤3，解得：x≤133．解：去括号得，10x+6≤x﹣3+6x，移项合并同类项得，3x≤﹣9，解得x≤﹣334．解：去分母，得3〔x+2〕≤4﹣x+6〔2分〕去括号，得3x+6≤4﹣x+6移项，得3x+x≤4+6﹣6〔4分〕合并同类项，得4x≤4两边同除以4，得x≤1移项，得5x﹣6x＞2+5，合并同类项，得﹣x＞7，系数化为1，得x＜﹣7．36. 去分母，得5〔3x+1〕﹣3〔7x﹣3〕≤30+2〔x﹣2〕，去括号，得15x+5﹣21x+9≤30+2x﹣4，移项，得15x﹣21x﹣2x≤30﹣4﹣5﹣9，合并同类项，得﹣8x≤12，系数化为1，得x≥﹣1.537．解：原不等式的两边同时乘以4，并整理得x﹣7＜3x﹣2，移项，得﹣2x＜5，不等式的两边同时除以﹣2〔不等式的符号的方向发生改变〕，得x ＞，故原不等式的解集是x ＞38．4x+3≥3x+5．解：移项、合并得x≥2．39．解：2〔x+2〕≥4〔x﹣1〕+7，2x+4≥4x﹣4+7，2x﹣4x≥﹣4+7﹣4，﹣2x≥﹣1，40．解：去分母得1+2x＞3x﹣3，移项得2x﹣3x＞﹣3﹣1，合并同类项得﹣x＞﹣4，解得x＜441．解：去括号，得6﹣2x＜x﹣3，移项、合并同类项，得﹣3x＜﹣9，化系数为1，得x＞342．解：去括号得，3x+6≤5x﹣5+7，移项得，3x﹣5x≤2﹣6，合并同类项得，﹣2x≤﹣4系数化为1，得x≥243．解：去分母，原不等式的两边同时乘以6，得6﹣3x+1≥2x+2，移项、合并同类项，得5x≤5，不等式的两边同时除以5，得x≤1合并同类项，得：﹣x＞﹣6，那么x＜645．解：去括号，得：2﹣4x+5≤6﹣3x，移项，得：﹣4x+3x≤6﹣2﹣5，合并同类项，得﹣x≤1，解得x≥﹣146．解；去分母得：x+1﹣6≤6x移项得：x﹣6x≤6﹣1合并同类项得：﹣5x≤5系数化1得：x≥﹣147．解：去分母得：7x+4﹣12＞12〔x+1〕，去括号得：7x+4﹣12＞12x+12，移项得：7x﹣12x＞12+12﹣4，合并同类项得：﹣5x＞20，系数化为1得：x＜﹣448．解：去分母得：16﹣〔3x﹣2〕＞24+2〔x﹣1〕16﹣3x+2＞24+2x﹣2﹣3x﹣2x＞24﹣2﹣16﹣2﹣5x＞4x＜﹣49．解；去括号得，4x+12﹣＜4﹣2x﹣x+，移项合并同类项得，7x＜﹣1，把x的系数化为1得，x＜﹣，50．解：不等式的两边同时乘以12，得3〔x+1〕﹣2〔2x﹣3〕≤12，即﹣x+9≤12，不等式的两边同时减去9，得﹣x≤3，不等式的两边同时除以﹣1，得x≥﹣3，∴原不等式的解集是x≥﹣3。

2020-1六下双基训练300题方程与不等式六年级·寒假·学生版九层之台，起于累土【练习1.1】 简单的一元一次方程1. ()()43206711y y y y --=--2. ()254(3)2(1)x x x --+=-3. 37(1)32(3)x x x --=-+4. 12(1)4()2x x x --=-5. 4(4)35(72)y y +=--6. 7 2.5 2.536x x -=⨯+7. 12(23)3(21)a a -+=-+ 8. 93(1)6x x --=9. 63(32)6(2)x x x --=-+ 10. 7104(0.5)x x -=-+方程与不等式补充材料千里之行，始于足下11. 3(8)64(11)y y y -=-- 12. 13(8)2(152)x x --=-13. 2(10)52(1)x x x x -+=+- 14.223046m m +--=15. 43(20)67(9)x x x x --=-- 16. 2(21)2(1)3(3)x x x -=+++17. 43(23)12(4)x x x +-=-- 18. ()()335225x x -=--19. ()()()243563221x x x --=--+ 20. ()()()321531152x x x --+=+六年级·寒假·学生版九层之台，起于累土【练习1.2】 一元一次方程——去分母21. 21101211364x x x --+-=- 22. 212153x x +--=23. 3157146y y ---= 24. 212134y y -+-=-25. 341125x x -+-= 26. 1112222x x x ⎡⎤⎛⎫---= ⎪⎢⎥⎝⎭⎣⎦27. 12233xx -=-+ 28.13216222x x x ⎛⎫--=+ ⎪⎝⎭方程与不等式补充材料千里之行，始于足下29. 21101136x x ++-= 30.211135x x +-=- 31. 121224x x+--=+ 32.42571510x x +--= 33. 124123x x ---= 34.213124x x--=- 35. 2123134x x ---= 36.3141136x x x ---=-六年级·寒假·学生版九层之台，起于累土37. 211135x x +-=- 38.+4122523x x x -+-=- 39. 25316412x x x ---+= 40. 2523163x x x +--=- 41. 431432x x -+-= 42.()()11212223x x x ⎡⎤--=+⎢⎥⎣⎦ 43. 141123x x --=- 44.5415513412y y y +--+=-方程与不等式补充材料千里之行，始于足下45. 121225x x ++-=- 46.()10532327x x x -++--=47. 7151322324x x x -++-=- 48.34113843242x x ⎧⎫⎡⎤⎛⎫--=⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭ 49. 248539x x -=- 50.3121134x x -+-= 51. 1122254x x x++--=+ 52.1328237x x x-+---=六年级·寒假·学生版九层之台，起于累土53. 248236x x ---=- 54.31322322105x x x +-+-=- 55. 225353x x x ---=- 56. 1212323x x x --+=- 57. 12136x x x -+-=- 58.3157146y y ---= 59. 131224x x+--=- 60.21101211364x x x -++-=-方程与不等式补充材料千里之行，始于足下61. 211011412x x x ++-=- 62.()()142113233x x x ⎡⎤+-=-+⎢⎥⎣⎦ 63. 312423(1)32x x x -+-+=- 64.49325532x x x ++--= 65. 4115(2)13212x x x +--+=-66. 113(23)(32)5(32)(23)32x x x x ---=-+-六年级·寒假·学生版九层之台，起于累土67. 22(31)253y y -=- 68.31242233x x ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦69. 21101211364x x x -++-=- 70.3213(1)(32)(1)45102x x x --+=-- 71. 431261345x ⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦72.121146x x ++-= 73. 211011412x x x ++-=- 74.111(15)(7)523x x +=--方程与不等式补充材料75. 2110121123644x x x-++-=-76.2383236x x x-+-=-77. 1010210147x x+--=78. ()()137464722x x-=+-79.12223x xx-+-=-80.3221211245x x x+-+-=-81. 13533236524x x⎛⎫⎛⎫---=⎪ ⎪⎝⎭⎝⎭82.112132152yy-+-=六年级·寒假·学生版83. 343111243242x x⎡⎤⎛⎫--=+⎪⎢⎥⎝⎭⎣⎦84.111116412345x⎧⎫⎡⎤⎛⎫--+=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭85.43254xxx x---=【练习1.3】一元一次方程——去分子、分母中的小数86. 0.10.20.710.30.4x x---=87.1.5 1.51.50.30.1x x--=88.2130.20.5x x-+-=89.0.30.2 1.5570.20.5x x--+=方程与不等式补充材料90. 0.20.10.010.0150.30.04x x---=91.0.010.030.40.110.020.5x x-+-=92.30.412.50.20.5x x+--=-93.341.60.50.2x x-+-=94. 2 1.633180.30.63x x x-+-=95.341.650.2y y-+-=96. 4 1.550.8 1.230.50.20.1x x x----=+97.1.5210.30.2x x--=六年级·寒假·学生版98. 3 1.50.20.1840.20.09x xx--+=+99.0.12230.30.6x xx-+-=100.341.60.50.2x x-+-=101.10.2110.40.7x x+--=102.0.230.210.50.03x x--=103.3 1.140.20.160.70.40.30.06x x x----=104. 1.510.530.6x x--=105.0.10.020.10.10.30.0020.05x x-+-=方程与不等式补充材料106. 0.030.010.170.050.10.020.070.030.09x x x +-+-=107. 0.10.20.0226.57.50.010.02x x---=-108.30.70.310.80.4x xx+-=-109. 0.40.50.20.5110.060.232x xx+-⎛⎫-=+⎪⎝⎭110.2651430.030.30.02x x-+-=【练习1.4】一元一次方程——巧算（整体法、拆括号、裂项、凑分子）111. 11311377325235x x⎛⎫⎛⎫--=--⎪ ⎪⎝⎭⎝⎭112. ()()15201520153411131717x x x---+=六年级·寒假·学生版113. ()()()()1131121132x x x x +--=--+ 114. 31333447167x x x x ⎡⎤⎛⎫⎛⎫---=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 115. ()()1123233211191313x x x -+-+=116. ()()()()1120181120191120182019x x x x +--=--+ 117. 111123452345x x x x +++=+++方程与不等式补充材料118. ()()()()1111123201620162342017x x x x ++++++++= 119. 111133312222y ⎧⎫⎡⎤⎛⎫---=⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭120.111246819753x ⎧⎫⎡⎤+⎛⎫+++=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭121. 2016122320162017x xx +++=⨯⨯⨯ 122. 1122320192020x xx+++=⨯⨯⨯123. 200613352003200520052007x x x x++++=⨯⨯⨯⨯六年级·寒假·学生版124.11 123234201720182019201820192020220192020 x x x x++++=-⨯⨯⨯⨯⨯⨯⨯⨯⨯125.3213201520162017x x x---++=126.201013201920092007x x x---++=127.2017130 1008620162014x x x---++=128.20181614125 357911x x x x x-----++++=方程与不等式补充材料129. 3x a b x b c x c ac a b------++= ()000a b c >>>、、 130.4x a b c x b c d x c d a x d a bd a b c------------+++= () a b c d 、、、均为正数【练习2.1】 较简单的二元一次方程131. 27325x y x y -=⎧⎨+=⎩132. 85765476x y x y +=⎧⎨-=⎩133. 293x y x y -=-⎧⎨+=⎩134. 53702370x y x y --=⎧⎨+-=⎩六年级·寒假·学生版135.5120311120x yy x-=⎧⎨-=⎩136.245x yx y+=⎧⎨-=⎩137.5210x yx y+=⎧⎨+=⎩138.25342x yx y-=⎧⎨+=⎩139.7423624x yx y+=⎧⎨-=⎩140.892317674x yx y+=⎧⎨-=⎩141.()()()()31445135y xx y⎧-=-⎪⎨-=+⎪⎩142.32222m nm n+=⎧⎨-=-⎩方程与不等式补充材料143.372513x yx y-=⎧⎨+=⎩144.25342x yx y-=⎧⎨+=⎩145.30327xx y-=⎧⎨-=⎩146.633594x yx y-=-⎧⎨-=⎩147.2114327x yx y+=⎧⎨+=⎩148.3(1)4(4)5(1)3(5)y xx y-=-⎧⎨-=+⎩149.()()()()4395211x y x yx y x y⎧+--=⎪⎨-++=⎪⎩150.()()()()337242233228x yx y⎧+=-+⎪⎨-+-=⎪⎩六年级·寒假·学生版【练习2.2】较复杂的二元一次方程组151.1234x yx y+=⎧⎪⎨+=⎪⎩152.1640.30.4 1.7x yx y⎧+=⎪⎨⎪+=⎩153.2320.40.7 2.8x yx y⎧+=⎪⎨⎪+=⎩154.35723423235x yx y++⎧+=⎪⎪⎨--⎪+=⎪⎩155.2()1346()4(2)16x y x yx y x y-+⎧=-⎪⎨⎪+=-+⎩156.2344143m n n mnm+-⎧-=⎪⎪⎨⎪+=⎪⎩方程与不等式补充材料157. 2153224111466x y x y ⎧+=-⎪⎪⎨⎪-=-⎪⎩158. 32212453231045x y x y --⎧+=⎪⎪⎨++⎪-=⎪⎩159. 252234m nm n ⎧-=⎪⎨⎪+=⎩160. ()()35724310413x y y x x y x y -+⎧+=-⎪⎪⎨---⎪=⎪⎩161. ()()()54723187323x y x y x y x y ⎧+-+=⎪⎪⎨⎪+--=⎪⎩162. 2164622372y x y x y x x y++⎧-=-⎪⎨⎪+=--⎩六年级·寒假·学生版163.1115212355x yyx+-⎧-=-⎪⎪⎨⎪+=-⎪⎩164.3223132x y x y-+==165.()5111562347 896x y y x x y---+++==【练习2.3】普通的三元一次方程组166.321x y zx y zx y-+=-⎧⎪+-=⎨⎪+=⎩167.324230140x yx zx y z=-⎧⎪-=⎨⎪++=⎩方程与不等式补充材料168.153241341013x y zx y zz-+=⎧⎪+-=-⎨⎪=⎩169.1225224x y zx y zx y++=⎧⎪++=⎨⎪=⎩170.3232443210x y zx y zx y z-+=⎧⎪+-=⎨⎪++=-⎩171. 235532z x yx y zx y z=+⎧⎪-+=⎨⎪+-=⎩172.52621212x yy zx z-=⎧⎪-=-⎨⎪+=⎩173.12232a b ca b ca b c++=⎧⎪+-=⎨⎪-+=⎩六年级·寒假·学生版174.3123325x y zx y zx y z+-=⎧⎪-+=⎨⎪+-=⎩175.261218x y zx yx y z++=⎧⎪-=⎨⎪-+=⎩176.102317328x y zx y zx y z++=⎧⎪++=⎨⎪+-=⎩177.42314235x y zx y zx y z--=⎧⎪++=⎨⎪+-=⎩178.4329253456218x y zx y zx y z-+=⎧⎪+-=⎨⎪+-=⎩179.24+393251156713x y zx y zx y z+=⎧⎪-+=⎨⎪-+=⎩方程与不等式补充材料180.232623343239x y zx y zx y z++=⎧⎪++=⎨⎪++=⎩181.3213272312x y zx y zx y z++=⎧⎪++=⎨⎪+-=⎩182.4239328a b ca b ca b c++=⎧⎪++=⎨⎪++=⎩183.261218x y zx yx y z++=⎧⎪-=⎨⎪-+=⎩184.56812412345x y zx y zx y z+-=⎧⎪+-=-⎨⎪+-=⎩185.24393251156713x y zx y zx y z++=⎧⎪-+=⎨⎪-+=⎩六年级·寒假·学生版186.9202325x y zx y zx y z-+=⎧⎪++=⎨⎪--=⎩187.261218x y zx yx y z++=⎧⎪-=⎨⎪-+=⎩188.231332163510x y zx y zx y z++=⎧⎪+-=⎨⎪+-=⎩189.3423126x y zx y zx y z-+=⎧⎪+-=⎨⎪++=⎩190.275323342y xx y zx z=-⎧⎪++=⎨⎪-=⎩191.344635511x y zx y zy z++=⎧⎪-+=-⎨⎪+=⎩方程与不等式补充材料192.42325560x y zx y zx y z-+=⎧⎪++=⎨⎪++=⎩193.52574313x yy zz x+=⎧⎪-=-⎨⎪+=⎩194.42325560a b ca b ca b c-+=⎧⎪++=⎨⎪++=⎩195.2343327231a b ca b ca b c-+=⎧⎪-+=⎨⎪+-=⎩【练习2.4】有技巧的多元一次方程组196.78388737x yx y+=⎧⎨+=⎩197.231763172357x yx y+=⎧⎨+=⎩六年级·寒假·学生版198.199519975989199719955987x yx y+=⎧⎨+=⎩199.354x yy zx z+=⎧⎪+=⎨⎪+=⎩200.222426x y zx y zx y z++=⎧⎪++=⎨⎪++=⎩201.1131x y zy z xz x y+-=⎧⎪+-=⎨⎪+-=⎩202.512x yy zz x+=⎧⎪+=-⎨⎪+=-⎩203. 2345238x y zx y z⎧==⎪⎨⎪+-=⎩方程与不等式补充材料204.::z1:2:32318x yx y z=⎧⎨-+=⎩205.:3:2:5:466x yy zx y z=⎧⎪=⎨⎪++=⎩206.323232y z x az x y bx y z c+-=⎧⎪+-=⎨⎪+-=⎩207.252821126x yy zz uu x+=⎧⎪+=⎪⎨+=⎪⎪+=⎩208.12323434545151212345x x xx x xx x xx x xx x x++=⎧⎪++=⎪⎪++=⎨⎪++=⎪⎪++=⎩209.12323434545151251532x x xx x xx x xx x xx x x++=⎧⎪++=⎪⎪++=-⎨⎪++=-⎪⎪++=⎩六年级·寒假·学生版210. 220240280+216023202640a b c d e f a b c d e f a b c d e f a b c d e f a b c d e f a b c d e f +++++=⎧⎪+++++=⎪⎪+++++=⎪⎨++++=⎪⎪+++++=⎪+++++=⎪⎩【练习3.1】 一元一次不等式 211. ()25321x x --≥ 212. 8156x x -≥-213. ()()3129x x -≤+ 214. ()()32232x x x x ⎡--⎤>--⎣⎦215. 3(2)152(2)x x -+-<-- 216.121123x x -++<方程与不等式补充材料217. 21433x x -≥-- 218. 3453172y y y --≤-219. 6721251423x x x --+-+>+- 220.121180.50.25x x -++>221. 124816x x x xx ++++> 222.12123x x +-≥223. 2354124463x x x ---+->+ 224. ()()52186117x x -+<-+六年级·寒假·学生版225. ()332524y y +≤- 226.()311212423x ⎡⎤--≥⎢⎥⎣⎦227. 11111112332x x ⎛⎫⎛⎫-≥-- ⎪ ⎪⎝⎭⎝⎭228. ()21035127x x x ---≥-229. 531132x x +--< 230. 22252y y y ---≤- 231. 123x x-< 232.2352x x -≥+方程与不等式补充材料233. 212(12)13x x --≥- 234.8111122x x x ++-≤-235. 422(2)x x -≥+ 236.3122123x x---≤237. 214432x x -+-< 238. 3(2)12(1)x x +>---239. 111(2)(3)248x x ->-+ 240. 533(2)x x +≤+六年级·寒假·学生版241. 14232x x -+->- 242.2432x x -≥- 243. 11132x x --≥ 244. 7(4)2(43)4x x x ---<245. 5(2)86(1)7x x -+<-+ 246.1132x x --< 247. 21211362x x x +--->- 248.3(1)5182x x x +-->-方程与不等式补充材料249.18136x xx+-+≤-250. 15(31)10(42)6(63)39x x x---≥--251. 0.40.210.20.5x x+->-252. 51531x x+>-253. 22123x x+-≥254.2(1)12xx---<255. 2152246x x-+-≥-256.3(1)12384x x+-+<-六年级·寒假·学生版257.121133x xx-+-≤+258.0.2 1.20.120.130.30.05x x---≤-259.()0.20.10.2 0.030.010.70.310.030.50.15x x x-+--<+260. 0.40.90.030.0250.50.032x x x++-->【练习3.2】一元一次不等式组261.3312183(1)xxx x-⎧+≥+⎪⎨⎪+<+-⎩262.253(2)12135x xx+≤+⎧⎪-⎨+>⎪⎩方程与不等式补充材料263. 22531323213x xx x--⎧-≤⎪⎨⎪->-⎩264. 3(1)954x x +≤⎧⎨+>⎩265. 3(1)702423x x x -->⎧⎪-⎨>⎪⎩266. 2362523x x x x +≤+⎧⎪+⎨<+⎪⎩267. 21390x x >-⎧⎨-+≥⎩268. 33(3)21123x x x x +≤+⎧⎪-+⎨>-⎪⎩269. ()()1032561x x x +⎧>⎪⎨⎪+≥-⎩270. 3150728x x x ->⎧⎨-<⎩六年级·寒假·学生版271.312342x xx x-≤-⎧⎨-+>-⎩272.1232(3)3(2)6x xx x⎧->-⎪⎨⎪--->-⎩273.593(1)311122x xx x-<-⎧⎪⎨-≤-⎪⎩274.328212xx-<⎧⎨->⎩275.523(4)131722x xx x-≤+⎧⎪⎨-<-⎪⎩276.328654x--≤--<-277.2632145x xx x-≤-⎧⎪+⎨->⎪⎩278.121233(2)54x xx x--⎧≤⎪⎨⎪+>+⎩方程与不等式补充材料千里之行，始于足下279. ()32421152x x x x ⎧--≥⎪⎨-+≤⎪⎩280. 513(1)23722x x x x ->+⎧⎪⎨-≤-⎪⎩281. 2132(1)5x x +⎧<⎪⎨⎪-≤⎩282. 312128x x x -≤+⎧⎨-<⎩283. 222212x x x x+⎧≥⎪⎨⎪-<-⎩284. 313112123x x x x +<-⎧⎪++⎨≤+⎪⎩285. 521262(3)4x x x x -⎧->⎪⎨⎪-≤-⎩ 286. 2153712x x x ->⎧⎪⎨-+≤⎪⎩六年级·寒假·学生版九层之台，起于累土287. 2(21)342151132x x x x -≤+⎧⎪-+⎨-≤⎪⎩288. 3(2)8143x x x x +>+⎧⎪-⎨≥⎪⎩289. 267442152x x x x +>-⎧⎪+-⎨≥⎪⎩290. 43213(1)6x x x x-⎧+≥⎪⎨⎪--<-⎩291. ()()35223141x x x x -⎧≤-⎪⎨⎪-<+⎩292. 543132(32)3x x x ->⎧⎨--≤⎩293. 2153112x x x ->⎧⎪⎨+-≥⎪⎩294. 253259837(4)2(43)4x x x x x x x +≤+⎧⎪->+⎨⎪---<⎩方程与不等式补充材料千里之行，始于足下295. ()1231121286432x x x x x x +>+-⎧⎪⎪+≥+⎨-<-⎪⎪⎩296. 8156212(12)133(2)152(2)x x x x x x -≥-⎧⎪-⎪-≥-⎨⎪-+-<--⎪⎩297. 36451322253522x x x x x x +>+-⎧⎪⎪+>+⎨<-⎪⎪⎩298. 18136212113620.40.210.20.5x x x x x x x x +-⎧+≤-⎪⎪+--⎪->-⎨⎪+-⎪>-⎪⎩299. 427323653453x x x x x x ⎧⎪+>++≥+≤-⎨-⎪⎩300. ()()32232217223x x x x x x ⎧⎪->++≤+≥+⎨-⎪⎩。

本讲在上一讲学习了一元一次不等式（组）的基础上，讲解一元一次不等式（组）的相关应用，以及含字母系数的不等式（组）和含绝对值的不等式．重点是灵活运用不等式的思想解决相关的实际问题，难点是掌握分类讨论的数学思想，用以解决含字母系数的不等式（组）和含绝对值的不等式的问题．1、 一元一次不等式及其解法只含有一个未知数且未知数的次数是一次的不等式叫做一元一次不等式． 解一元一次不等式的一般步骤： （1）去分母； （2）去括号； （3）移项；（4）化成ax b >（或ax b <等）的形式（其中0a ≠）；（5）两边同时除以未知数的系数，得到不等式的解集．一元一次不等式（组）的应用与提高内容分析知识结构模块一：一元一次不等式的解法及应用知识精讲【例1】()5134y y--≥-的最大整数解是__________．【难度】★【答案】4．【解析】原不等式化为：28y≤，即：4y≤，所以最大整数解是4．【总结】考查不等式的解法，注意题目中求的是最大整数解．【例2】解下列不等式．（1）7341112536x x x x-++--≥-+；（2）()()112335123x x⎡⎤----≥⎢⎥⎣⎦．【难度】★★【答案】（1）3617x≤；（2）23x≤-．【解析】（1）去分母得：15(7)6(34)3010(1)5(1)x x x x--+≥-++-去括号得：10515182430101055x x x x---≥--+-合并同类项得：3472x≤解得：3617x≤；（2）化简得：5(23)23x x---+≥，4(23x--≥，423x-≤-即原不等式的解为：23x≤-．【总结】考查不等式的解法，注意去分母时每一项都要乘以最简公分母．【例3】当a为何值时，不等式31324x a x-->的解集是x > 2．【难度】★★【答案】16．【解析】去分母得：2(31)3x a x->-，去括号化简得：92x a>+所以原不等式的解为：29ax+>，即229a+=，解得：16a=．【总结】本题主要考查对不等式的解集的理解及运用．例题解析【例4】m为何正整数时，关于x的方程5315424x m m-=-的解是非正数？【难度】★★【答案】m为1或2或3．【解析】去分母得：53215x m m-=-，化简得：3x m=-．因为方程的解是非正数，所以30m-≤，解得：3m≤，所以正整数m的值为1、2、3．【总结】考查解一元一次方程与解不等式的综合运用，注意对非正数的理解．【例5】有一个两位数，个位数字与十位数字的和是9，且这个两位数不大于63，求这个两位数．【难度】★★【答案】63或54或45或36或27或18．【解析】设这个两位数的十位数字为x，则个位数字为(9)x-，则有：10963x x+-≤，解得：6x≤，所以这个两位数可能为：63、54、45、36、27、18．【总结】考查不等式的简单应用．【例6】10名菜农，每人可种甲种蔬菜3亩或种乙种蔬菜2亩，已知甲种蔬菜每亩可收入0．5万元，乙种蔬菜可收入0．8万元，要使总收入不低于15．6万元，则最多能安排几个人种甲种蔬菜？【难度】★★【答案】4人．【解析】设安排x人种甲种蔬菜，则种乙种蔬菜的人数为（10x-）人，则0.530.82(10)15.6x x⨯+⨯-≥，解得：4x≤，故最多安排4人种甲种蔬菜．【总结】考查不等式在实际生活中的简单应用．【例7】 用含药率15%与40%的同种农药混合成含药率不小于30%的农药100千克，那么含药率40%的农药应不少于多少千克？ 【难度】★★【答案】不少于60千克．【解析】设需含药率15%的农药x 千克，则需含药率40%的农药（100x -）千克， 可列方程：15%40%(100)30x x +-=，解得：40x =，故10060x -=千克． 【总结】考查不等式在实际生活中的简单应用．【例8】 某单位组织旅游，定了若干条游船（不超过10条），如每条游船坐4人，则还余19人没安排；如每条游船坐6人，则有一条船人没坐满．问：该单位定了多少条游船？ 【难度】★★ 【答案】10条．【解析】设该单位定了x 条游船(010)x x <≤，为整数，则0(419)6(1)6x x <+--<，解得：9.510x <≤， 所以10x =，即该单位定了10条游船． 【总结】考查不等式的简单应用．【例9】 某班班主任组织优秀班干部去旅游，甲旅行社说：“如果班主任买全票一张，则其余学生可享受半价优惠．”乙旅行社说：“包括班主任在内全部按全票价的6折优惠．”全票价为24元/张，就学生数讨论哪家旅行社更优惠． 【难度】★★★ 【答案】见解析．【解析】设旅行社收的费用为y 元，学生数有x 人，根据题意得：24024050%120240(1)24060%144144y x x y x x =+⨯⨯=+=+⨯⨯=+甲乙，当y y =甲乙时，解得4x =，即当学生数为4时，两家旅行社收费一样多； 所以可得：当4x >时，y y <甲乙；当4x <时，y y >甲乙．因此学生数多于4人时，选甲旅行社；当学生数少于4人时，选乙旅行社． 【总结】考查不等式的应用，注意对两种方案的选择．【例10】 已知A 市和B 市库存某种机器12台和6台，现决定支援C 市10台，D 市8台，已知从A 市调运一台机器到C 市、D 市的运费分别为400元和800元；从B 市调运一台机器到C 市、D 市运费分别300元和500元，要求运费不超过9000元，问共有几种调运方案． 【难度】★★★ 【答案】见解析．【解析】设B 市到C 市运x 台，则B 市到D 市运（6x -）台，A 市到C 市运（10x -）台， A 市到D 市运（12(10)x --）台，总运费为ω元，则 300500(6)400(10)800[12(10)]x x x x xω=+-+-+--=+，令9000ω≤，即20086009000+≤，解得：2x ≤． 所以共有三种调运方案：①B 市往C 市运0台，B 市往D 市运6台，A 市往C 市运10台，A 市往D 市运2台； ②B 市往C 市运1台，B 市往D 市运5台，A 市往C 市运9台，A 市往D 市运3台； ③B 市往C 市运2台，B 市往D 市运4台，A 市往C 市运8台，A 市往D 市运4台． 【总结】考查不等式的应用，注意对方案的选择．【例11】 解不等式：34312xx->-． 【难度】★★★【答案】102x <<．【解析】移项得：343012x x -->-，通分得：343(12)012x x x --->-，即2012xx>-． 1． 当0120x x >->，且时，解得：102x <<； 2．当0120x x <-<且时，不等式无解． 综上原不等式的解集为：102x <<． 【总结】本题综合性较强，注意分类讨论，切忌直接去分母．1、 解一元一次不等式组的一般步骤（1）求出不等式组中各个不等式的解集； （2）在数轴上表示各个不等式的解集；（3）确定各个不等式解集的公共部分，就得到这个不等式组的解集．【例12】 不等式3941x -<-<的解集是__________． 【难度】★ 【答案】23x <<．【解析】移项：39419x --<-<-，两边同时除以-4：1248x -<-<-，解得：23x <<． 【总结】考查不等式组的解法．【例13】 同时满足不等式23104x-+≥和()225x -≥-的整数解是______________． 【难度】★★ 【答案】0、1、2．【解析】由第一个不等式可得：2340x -+≥，解得：2x ≤，由第二个不等式可得：245x -≥-，解得：12x ≥-，所以：122x -≤≤，故满足不等式组的整数解是：0、1、2．【总结】考查不等式组的解法及应用，注意对整数解的确定．模块二：一元一次不等式组的解法与应用知识精讲例题解析【例14】 x 的2倍与5的和的一半大于3-且不大于7，列出不等式（组）为____________，x 的取值范围为__________________． 【难度】★★ 【答案】见解析． 【解析】根据题意得：25372x +-<≤，解得：11922x -<≤． 【总结】考查不等式组的应用及解法．【例15】 不等式组()12143x ax x +<⎧⎪⎨->-⎪⎩的解集为一切负数，求a 的值．【难度】★★ 【答案】1．【解析】由①得：1x a <-，由②得：112x <，因为不等式组的解集为一切负数， 所以1x a <-，且101a a -==，解得：． 【总结】考查对不等式组的解集的理解及简单应用．【例16】 解下列不等式组： （1）1032752532x x x x x --⎧+-<-⎪⎪⎨⎪+>+⎪⎩；（2）()()22132237223x x x x x x ⎧+≤+⎪->+⎨⎪-≥+⎩．【难度】★★． 【答案】见解析【解析】（1）由①得：10(2)2(10)705(3)x x x +--<--，化简得：1345x <，解得：4513x <，由②得：4x >-， 所以原不等式组的解集为：45413x -<<； （2）由①得：1x ≥，由②得：5x >，由③得：4x ≥，所以原不等式组的解为：5x >．【总结】考查不等式组的解法：同大取大，同小取小，小大大小取中间，大大小小是空集．【例17】 一件商品售价为120元，若按售价九折出售，获利不超过20%；若按售价七折出售，则出现亏本．求商品成本价的范围．【难度】★★ 【答案】见解析．【解析】设商品成本价为x 元，由题意可得：12090%120%12070%x x ⨯≤+⎧⎨⨯<⎩，解得：9084x x ≥⎧⎨>⎩， 所以原不等式组的解集为：90x ≥．【总结】考查不等式组在实际问题中的简单应用．【例18】 一种灭虫药粉40千克，含药率是15%，现在要用含药率较高的同样的灭虫药粉50千克与它混合，使混合后的含药率在25%与30%之间（不包括25%和30%），求所用药粉的含药率的范围． 【难度】★★ 【答案】见解析．【解析】设所用药粉的含药率为x ，由题意可得：4015%5025%30%4050x ⨯+<<+，解得：33%42%x <<， 即所用药粉的含药率在33%到42%之间．【总结】考查不等式组的简单应用，注意对含药率的准确理解．【例19】 某初三毕业班若干名同学合影留念，需交照相费40元（含两张照片），若另外加洗一张照片收费5元，预定平均每人交钱大于6元而少于8元，问：至少有多少学生参加照相，才能保证一人一张照片？ 【难度】★★ 【答案】11．【解析】设有x 名学生参加照相，由题意可得：6405(2)8x x x <+-<，解得：1030x <<，因为学生数为整数，所以至少有11名同学．【总结】考查不等式组在实际问题中的简单应用，注意学生数只能取整数．【例20】 某工厂现有甲种原料360千克，乙种原料290千克，计划用这两种原料生产A 、B 两种产品共50件，已知生产一件A 种产品需要甲种原料9千克，乙种原料3千克，出售后可获利700元；生产一件B 种产品需要甲种原料4千克，乙种原料10千克，出售后可获利1200元．按要求安排A 、B 两种产品的生产件数，有哪几种方案？哪种方案获利最大？最大利润是多少？ 【难度】★★★ 【答案】见解析．【解析】设生产A 种产品x 件，则有：94(50)360310(50)290x x x x +-≤⎧⎨+-≤⎩，解得：3032x ≤≤，所以有三种方案：①生产A 种产品30件，B 种产品20件；此时获利：7003012002045000⨯+⨯=元； ②生产A 种产品31件，B 种产品19件；此时获利：7003112001944500⨯+⨯=元； ③生产A 种产品32件，B 种产品18件；此时获利：7003212001844000⨯+⨯=元， 所以采用方案①所获利润最大，为45000元．【总结】本题综合性较强，主要考查不等式组在实际问题中的应用．【例21】 某厂2016年12月在制定2017年某种化肥的生产计划时，收集到了如下信息： 生产该化肥的工人数不能超过200人；每个工人全年工时数不得多于2100个；预计2017 年该化肥至少可销售80000袋；每生产一袋该化肥需要4个工时；每袋该化肥需要原料 20千克；现库存原料800吨，本月还需要200吨，2017年可补充1200吨． 请你根据以上数据确定2017年该种化肥的生产袋数的范围． 【难度】★★★【答案】8000090000x ≤≤．【解析】设2017年该种化肥的生产袋数为x ，则根据题意，可得：4210020020(8002001200)10008000x x x ≤⨯⎧⎪≤-+⨯⎨⎪≥⎩由①得：105000x ≤， 由②得：90000x ≤所以8000090000x ≤≤，即2017年生产袋数范围是8000090000x ≤≤． 【总结】本题综合性较强，主要考查不等式组在实际问题中的应用．【例22】甲、乙两人到某折扣店买商品，商店的商品只剩两种，单价为32元和36，已知两人购买商品的件数相同，且两人购买商品一共花费了688元，求两人共购买两种商品各多少件？【难度】★★★【答案】8、12．【解析】设单价为32元的购买x件，36元的y件，则3236688x y+=，化简得：8()172x y y++=，因为x、y均为整数，所以解得812xy=⎧⎨=⎩，即两人共购买甲商品8件，乙商品12件．【总结】本题综合性较强，主要考查不等式组在实际问题中的应用．【例23】已知a、b、c为三个非负数，且满足325a b c++=，231a b c+-=，若39S a b c=+-，则S的最大值与最小值为多少？【难度】★★★【答案】见解析．【解析】由325231a b ca b c++=⎧⎨+-=⎩①②，得73711a cb c=-⎧⎨=-⎩③④，所以393(73)71192 s a b c c c c c=+-=-+--=-．因为a、b、c为三个非负数，故由③得：730a c=-≥，37c≥，由④得：7110b c=-≥，711c≤，所以37711c≤≤，则当711c=时，s值最大，为1511-；当37c=时，s值最小，为137-．【总结】本题较复杂，主要考查不等式组的应用，注意用一个未知量去表示另一个未知量．1、 含字母系数的不等式根据不等式的性质3可知：对于不等式1ax >，若0a >，则1x a >；若0a <，则1x a<．【例24】 解关于x 的不等式()120a x a --+>（其中a > 1）． 【难度】★ 【答案】21a x a ->-． 【解析】由题意可得：(1)2a x a ->-，因为a > 1，所以10a ->，所以21a x a ->-． 【总结】考查不等式的解法，注意对字母系数的正负的判定．【例25】 讨论关于x 的不等式ax < b （0a ≠）的解的情况． 【难度】★★ 【答案】见解析． 【解析】当0a >时，b x a <； 当0a <时，bx a>． 【总结】考查解含字母系数的不等式，注意分类讨论．【例26】 设a < 1，解不等式1ax a x +-<． 【难度】★★ 【答案】1x >-．【解析】由题意可得：(1)1a x a -<-，因为a < 1，所以10a -<， 所以原不等式的解为1x >-．【总结】考查不等式的解法，注意对字母系数的正负的判定．模块三：含字母系数的不等式（组）知识精讲例题解析【例27】 解关于x 的不等式2m x n x ->+． 【难度】★★ 【答案】21nx m <-+． 【解析】由题意可得：2m x x n -->，即2(1)m x n -+>， 因为2(1)0m x -+<，所以原不等式的解为21nx m <-+． 【总结】考查不等式的解法，注意对字母系数的正负的判定．【例28】 已知关于x 的不等式()3223a x a -<-的解集是1x >-，求a 的取值范围． 【难度】★★★【答案】23a <．【解析】由题意可得：320a -<，解得：23a <． 【总结】考查对不等式的解集的理解及应用．【例29】 设不等式()()230a b x a b ++-<的解集是13x <-，解关于x 的不等式()32a b x a b ->-．【难度】★★★ 【答案】3x <-．【解析】由题意可得：不等式的解集为：32b ax a b-<+， 3213b a a b -∴=-+，解得2a b =，代入()32a b x a b ->-，得：3bx b ->． 0320200a b b a a b a b +>-<=∴>>，且，，，()323x a b x a b x ∴->-<-的解集的式为：关于不等．【总结】本题综合性较强，要先根据第一个不等式的解集，求出a 、b 之间的关系，从而再求出第二个不等式的解集，注意要根据已知条件判断系数的符号．1、 ax b c +>（0c >）的解法是：先化为不等式组ax b c +>或ax b c +<-，再由不等式的性质求出原不等式的解集． 2、 ax b c +<（0c >）的解法是：先化为不等式c ax b c -<+<，再由不等式的性质求出原不等式的解集．【例30】 下列不等式中，解集为一切实数的是（ ）A ．21x +>B ．211x ++>C ．()2781x ->-D ．()27810x -->【难度】★ 【答案】C【解析】A 、B 选项当x 取-2时不成立； C 选项()2780x -≥所以不论取何值时都是成立的； D 选项当x 取78时不成立． 【总结】考查绝对值的非负性的运用．【例31】 解绝对值不等式． （1）23x -≤；（2）23x ->．【难度】★★【答案】（1）15x -≤≤；（2）51x x ><-或． 【解析】（1）323x -≤-≤，解得：15x -≤≤； （2）23x ->或23x -<-，解得：51x x ><-或． 【总结】考查含绝对值符号的不等式的解法．模块四：含绝对值符号的不等式知识精讲例题解析【例32】 解不等式125x -<． 【难度】★★ 【答案】23x -<<．【解析】由题意得：5125x -<-<，即：624x -<-<，解得：23x -<<． 【总结】考查含绝对值符号的不等式的解法．【例33】 不等式组1122210x x ⎧-≥⎪⎨⎪-<⎩的解集为____________．【难度】★★ 【答案】82x -<≤-．【解析】由题意：由①得：2x ≤-；由②得：812x -<<，所以不等式组的解集为：82x -<≤-． 【总结】考查含绝对值符号的不等式的解法．【例34】 解不等式组：431013x ≤-<． 【难度】★★★ 【答案】见解析．【解析】由题意可得：1331013x -<-<、31043104x x -≥-≤-或，解得：2313x -<<；1423x x ≤≥或，所以原不等式组的解为：14231233x x -<≤≤<或． 【总结】考查含绝对值符号的不等式的解法，注意解集取公共部分．【例35】 解不等式：211x x +>+． 【难度】★★★【答案】23x <-或0x >．【解析】①若210x +≥，即12x ≥-时，有211x x +>+，解得：0x >，②若210x +<，即12x <-时，有211x x -->+，解得：23x <-，综上，不等式的解集为：23x <-或0x >．【总结】考查含绝对值符号的不等式的解法，注意分类讨论．【例36】 解不等式：211x x -+>． 【难度】★★★ 【答案】203x x ><-或． 【解析】由题意，不等式可化为：211211x x x x -+>-+<-或， 整理得：211211x x x x +<-+>+或，由①可得：210210211211x x x x x x +>+<⎧⎧⎨⎨+<---<+⎩⎩或，此时无解，由②得：210210211211x x x x x x +>+<⎧⎧⎨⎨+>+-->+⎩⎩或，解得：203x x ><-或，综上原不等式的解集为：203x x ><-或． 【总结】考查含绝对值符号的不等式的解法，注意分类讨论．【习题1】 解下列不等式．（1）14153328x x ++≥--； （2）0.30.20.050.010.70.120.40.020.3x x x ++--≤-． 【难度】★★ 【答案】（1）394x ≥-；（2）4x ≤． 【解析】（1）由题意，去分母得：120884123x x -≥--，整理得：439x ≥-，解得：394x ≥-； （2）由题意化简得：3251712423x x x ++--≤-， 去分母得：9630624-284x x x +--≤+，整理得：728x ≤， 解得：4x ≤．【总结】考查不等式的解法，注意去分母时每一项都要乘以最简公分母．随堂检测【习题2】 解不等式组：（1）()()11373113365221038127x x x xx x x ⎧----<-⎪⎪⎨--⎪-<-⎪⎩；（2）342534127232310.54x xx x x x x x +<+⎧⎪-<-⎪⎪+⎨+<--⎪⎪-->⎪⎩．【难度】★★ 【答案】（1）613x >；（2）11x -<<． 【解析】（1）由①得：7055(3)18615(13)x x x x --<---， 整理得：18366x >，解得：613x >； 由②得：147(38)4(10)14x x x --<--，整理得：756264x x -+<-，解得：10x >， 所以原不等式组的解集是：613x >； （2）由①得：1x >-；由②得：2x <；由③得：1x <；由④得：2x >-， 所以原不等式组的解集是：11x -<<． 【总结】考查解不等式组的简单应用．【习题3】 若代数式32353x x -+-的值是非负数，则x 的取值范围是_______． 【难度】★★【答案】214x ≥．【解析】由题意可得：323053x x -+-≥，化简得：965150x x ---≥，解得：214x ≥． 【总结】考查不等式的简单应用，注意对非负数的准确理解．【习题4】 三个连续的正偶数的和不超过30，求这三个数． 【难度】★★． 【答案】见解析．【解析】由题意得：2222230n n n -+++≤，即6305n n ≤≤，，所以2345n =、、、， 所以这三个数为2、4、6或4、6、8或6、8、10或8、10、12． 【总结】考查不等式在实际问题中的简单应用．【习题5】公园门票，普通票每位10元，如买20人以上（含20人）的团体票则可8折优惠．现有18位游客买了20人的团体票，问比买普通票省了多少钱？如果不足20人，至少多少人买20人的团体票比买普通票省钱？【难度】★★【答案】省了20元；至少17人．【解析】（1）18位游客买20人的团体票所需费用为：20×10×80%=160元，这18为游客若买普通票则需要费用为18×10=180元，所以便宜180-160=20元；（2）设至少有x人，则：20 1020100.8xx<⎧⎨>⨯⨯⎩解得：1620x<<，所以至少17人．【总结】考查不等式的简单应用，解题时注意认真分析题意．【习题6】在爆破时，如果导火线燃烧的速度是0.8厘米/秒，人跑开的速度是5米每秒，那么点燃导火线的人要在爆破时能跑到100米以外的安全区域，导火线的长度应不小于多少米？【难度】★★【答案】0.16米．【解析】设导火线应该是x厘米．由题意得：0.81005x÷≥÷，解得：16x≥经检验符合题意，所以导火线的长度至少16厘米，即0.16米．【总结】考查不等式的简单应用，注意单位的统一．【习题7】某公司为了扩大经营，决定购进6台机器用于生产某种活塞．现有甲、乙两种机器供选择，其中每台机器的价格和每台机器日生产活塞的数量如下表所示．经过预算，（1）按该公司要求可以有几种购买方案？（2）若该公司购进的6台机器的日生产能力不低于380个，那么为了节约资金应选择哪种购买方案？【难度】★★【答案】见解析．【解析】设购买甲种机器x 台（0x ≥），则购买乙种机器(6)x -台，由题意得：75(6)34x x +-≤，解得：2x ≤，即可以取0、1、2三个值．所以有以下方案：方案①：不买甲，买乙6台，需资金6×5=30万元，日生产能力为6×60-360个， 方案②：买甲1台，买乙5台，需资金1×7+5×5=32万元， 生产能力为100+5×60=400个，方案③：买甲2台，买乙4台，需资金2×7+4×5=34万元，生产能力为2×100+4×60=440， 因此，选择方案②，既能达到生产能力又比方案③节约． 【总结】考查不等式的简单应用，注意对最优方案的选择．【习题8】 今有浓度5%、8%、9%的甲、乙、丙三种盐水分别为60克、60克、47克，现要配制7%的盐水100克，问甲种盐水最多可用多少克？最少可用多少克？【难度】★★★【答案】甲种盐水最多取49克，最少取35克．【解析】设甲乙丙盐水分别各取x 克、y 克、z 克，配成浓度为7%的盐水100克， 则有1005897%100x y z x y z ++=⎧⎨++=⨯⎩①②，其中060060047x y z ≤≤⎧⎪≤≤⎨⎪≤≤⎩③④⑤由①②得：20043100y x z x =-=-，，于是由④有：0200460x ≤-≤，解得：3550x ≤≤， 由⑤得：0310047x ≤-≤，解得：100493x ≤≤， 综上：3549x ≤≤，所以甲种盐水最多取49克，最少取35克． 【总结】考查不等式在实际问题中的应用，综合性较强，注意进行分析．【习题9】 解不等式：3315x -≥． 【难度】★★【答案】64x x ≥≤-或．【解析】由题意得：33153315x x -≥-≤-或，解得：64x x ≥≤-或． 【总结】考查含绝对值的不等式的解法．【习题10】 解关于x 的不等式ax b cx d +>+． 【难度】★★★ 【答案】见解析．【解析】由题意得：()a c x d b ->-，分类讨论如下：①当0a c ->时，原不等式的解为：d bx a c ->-； ②当0a c -<时，原不等式的解为：d bx a c-<-； ③当0a c -=，0d b -<时，原不等式有无数解； ④当0a c -=，0d b -≥时，原不等式无解．【总结】考查含字母系数的不等式的解法，注意分类讨论．【习题11】 如果不等式()312x a --≤的正整数解是1、2，求a 的取值范围． 【难度】★★★ 【答案】14a ≤<．【解析】由题意整理得：31x a ≤-，解得：13ax -≤， 因为原不等式的正整数解是1、2，则1233a-≤<，解得：14a ≤<． 【总结】考查不等式的应用，注意对解得取值范围的准确判定．【习题12】 已知关于x 的不等式()432a b x b a ->-的解集是49x <，求ax b >的解集． 【难度】★★★【答案】56x <．【解析】由题意得：430a b -<，24439b a x a b -<=-，得56b a =，即56ab =， 代入430a b -<，得0a <， 所以不等式ax b >的解集为：b x a<，即56x <．【总结】考查不等式的简单应用，注意对字母的正负进行判定．【作业1】 解下列不等式（组）．（1）31362232x x xx +--+≤-； （2）()()3116.5 5.52184y y y +--<-++； （3）427336452335x x x x x x +≥+⎧⎪+>+⎨⎪-≤-⎩．【难度】★★ 【答案】见解析．【解析】（1）化简得：31226(2x x x x ++-≤--，整理得31452x x x +-≤+， 解得原不等式的解集为：2513x ≥； （2）去分母得：523(1)442(1)16(1)y y y -+<--++，整理得：1713y >-， 解得原不等式的解集为：1317y >-； （3）由①得：15x ≤；由②得：592x >-；由③得：2x ≥， 可画图发现原不等式组无解． 【总结】考查解不等式的简单应用．【作业2】 下面四个结论中，正确的个数有（ ）（1）ax b =，当0a ≠时，解为b x a =； （2）ax b <，当0a ≠时，解集为bx a<；（3）ax b ->，当0a <，解集为b x a >-； （4）()21a x b +>-的解集为21bx a <-+．A ．1个B ．2个C ．3个D ．4个【难度】★★ 【答案】B【解析】（1）正确；（2）错误，本题需分类讨论；（3）正确；（4）错误，21bx a >-+，综上可得只有（1）、（3）正确，故选B ．【总结】考查不等式的解法，注意对字母系数的正负进行判定．课后作业【作业3】 已知不等式组212x a x a >+⎧⎨<-⎩无解，则a 的取值范围是（ ） A ．3a ≤-B ．3a <-C ．3a ≥-D ．3a >-【难度】★★【答案】C 【解析】由题意可得212a a +≥-，即3a ≥-，故选C ．【总结】考查不等式组的解法：大大小小是空集．【作业4】 a 的3倍与5的和不大于16与a 的差，求正整数a ．【难度】★★【答案】1或2．【解析】根据题意可得：3516a a +≤-，解得：114a ≤，所以正整数a 可能是1或2． 【总结】考查不等式的应用及解法．【作业5】 求使代数式23375x x ---的值不大于1的最大整数x ． 【难度】★★【答案】9．【解析】由题意可得：233175x x ---≤，去分母得5(23)7(3)35x x ---≤， 化简得：329x ≤，解得：293x ≤，所以x 的最大整数解为9． 【总结】考查不等式的简单应用．【作业6】 如果方程组42533x y k y x +=-⎧⎨-=⎩的解同号，求k 的取值范围． 【难度】★★【答案】732k k <->或． 【解析】由题意可得方程组的解为：618132713k x k y -⎧=⎪⎪⎨+⎪=⎪⎩，因为方程组的解同号， 得：6182701313k k -+⋅>，即(3)(27)0k k -+>，解得732k k <->或 【总结】本题主要考查不等式组与方程组的综合应用，注意“同号得正”的运用．【作业7】 把一箱苹果分给若干个小孩，如果每人分2个，还剩37个；如果每人分6个，那么最后一个小孩少于6个，求共有多少个小孩？【难度】★★【答案】10个．【解析】设有x 个小孩，由题意可得：662376x x x -<+<，解得：374344x <<，因为人数为整数，所以有10个小孩． 【总结】考查不等式在实际生活中的的简单应用．【作业8】 工程队原计划6天内完成300土方工程，第一天完成60土方，现决定比原计划提前2天超额完成，问后几天每天平均至少完成多少土方？【难度】★★【答案】80．【解析】设后几天平均每天完成x 土方．具根据题意有：60(612)30x +--≥，解得：80x ≥，即后几天平均每天至少完成80土方．【总结】考查不等式在实际生活中的的简单应用．【作业9】 某童装加工企业今年五月份，工人每人平均加工童装300套，最不熟练的工人加工的童装套数为平均套数的60%．为了提高工人的劳动积极性，按照完成完成外商订货任务，企业计划从六月份起进行工资改革．改革后每位工人的工资分两部分：一部分为每人每月基本工资900元；另一部分为每加工1套童装奖励若干元．（1）为了保证所有工人的每月工资收入不低于1260元，按五月份工人加工的童装套数计算，工人每加工1套童装企业至少应奖励多少元？（2）根据经营情况，企业决定每加工1套童装奖励5元．工人小张争取六月份工资不少于2000元，问小张在六月份应至少加工多少套童装？【难度】★★★【答案】（1）2元；（2）220套．【解析】（1）设企业每套奖励x 元，则90060%3001260x +⋅≥，解得：2x ≥；（2）设小张在六月份加工y 套，则90052000y +≥，解得：220y ≥，故工人每加工1套童装企业至少应奖励2元；小张在六月份应至少加工220套童装．【总结】考查不等式在实际问题中的简单应用，注意认真分析题目中的条件．【作业10】 解关于x 的不等式()()11ax x a a >++-．【难度】★★★【答案】见解析．【解析】由题意可得：(1)(1)(1)a x a a ->+-当10a ->时，解得：1x a >+；当10a -<时，解得：1x a <+．【总结】考查解含字母系数的不等式，注意分类讨论．【作业11】 解不等式组：2539x ≤-<． 【难度】★★★【答案】413x -<≤或71433x ≤<． 【解析】由题意：539532x x ⎧-<⎪⎨-≥⎪⎩①②，由①得：9539x -<-<，解得：41433x -<<； 由②得：532532x x -≥-≤-或，解得：713x x ≤≥或； 综上，原不等式组的解为413x -<≤或71433x ≤<． 【总结】本题综合性较强，主要考查含绝对值的不等式组的解法，最后注意引导学生用画图的方法帮助确定不等式组的取值范围．。

沪教版数学六年级下册6.6《一元一次不等式的解法》教学设计一. 教材分析《一元一次不等式的解法》是沪教版数学六年级下册第六章第六节的内容。

这一节主要让学生掌握一元一次不等式的解法，培养学生解决实际问题的能力。

教材通过生活中的实例引入一元一次不等式，然后引导学生通过观察、分析、归纳等方法，探索并掌握一元一次不等式的解法。

教材内容由浅入深，循序渐进，既注重了知识的发生发展过程，又重视了学生能力的培养。

二. 学情分析六年级的学生已经具备了一定的代数基础，对一元一次方程有一定的了解。

但是，对于一元一次不等式，他们还是初次接触，需要通过具体的生活实例来理解其意义。

另外，学生在解决实际问题时，常常会受到具体情境的干扰，难以将实际问题转化为数学问题。

因此，在教学过程中，我需要关注学生对一元一次不等式的理解，引导他们通过观察、分析、归纳等方法，探索并掌握一元一次不等式的解法。

三. 教学目标1.知识与技能：使学生理解一元一次不等式的概念，掌握一元一次不等式的解法，能够运用一元一次不等式解决实际问题。

2.过程与方法：培养学生观察、分析、归纳的能力，提高学生解决实际问题的能力。

3.情感态度与价值观：培养学生对数学的兴趣，使学生体验到数学在生活中的应用，增强学生自信心。

四. 教学重难点1.重点：一元一次不等式的概念，一元一次不等式的解法。

2.难点：一元一次不等式在实际问题中的应用。

五. 教学方法采用情境教学法、启发式教学法、小组合作学习法等，充分调动学生的学习积极性，引导学生通过观察、分析、归纳等方法，探索并掌握一元一次不等式的解法。

六. 教学准备1.教具：课件、黑板、粉笔。

2.学具：练习本、铅笔、橡皮。

七. 教学过程1.导入（5分钟）通过一个生活中的实际问题，引入一元一次不等式的概念。

例如：小华买了一本书，原价是12元，商店搞活动满30元减10元，小华需要花多少钱买这本书？引导学生列出不等式，解决问题。

2.呈现（10分钟）通过多媒体课件，呈现一组一元一次不等式，引导学生观察、分析，发现一元一次不等式的解法。

不等式计算题50道一、一元一次不等式1. 解不等式2x + 3>5- 解析：首先将常数项移到右边，得到2x>5 - 3，即2x>2。

然后两边同时除以2，解得x > 1。

2. 解不等式3x-1<8- 解析：先将常数项移到右边，3x<8 + 1，也就是3x<9。

两边同时除以3，解得x<3。

3. 解不等式(1)/(2)x+5≥slant3- 解析：先将常数项移到右边，(1)/(2)x≥slant3 - 5，即(1)/(2)x≥slant - 2。

两边同时乘以2，解得x≥slant - 4。

4. 解不等式4-(2)/(3)x>2- 解析：先将常数4移到右边，-(2)/(3)x>2 - 4，即-(2)/(3)x>-2。

两边同时乘以-(3)/(2)，不等号方向改变，解得x < 3。

5. 解不等式5x+2≤slant3x - 4- 解析：先将含x的项移到左边，常数项移到右边，5x-3x≤slant - 4 - 2，即2x≤slant - 6。

两边同时除以2，解得x≤slant - 3。

6. 解不等式2(x - 1)+3>3x- 解析：先展开括号2x-2 + 3>3x，即2x + 1>3x。

将2x移到右边，得到1>3x-2x，解得x < 1。

7. 解不等式3(x + 2)-1≥slant5x-2- 解析：展开括号得3x+6 - 1≥slant5x-2，即3x + 5≥slant5x-2。

移项3x-5x≥slant - 2 - 5，-2x≥slant - 7。

两边同时除以-2，不等号方向改变，解得x≤slant(7)/(2)。

8. 解不等式(3x - 1)/(2)<(2x+3)/(3)- 解析：两边同时乘以6去分母，得到3(3x - 1)<2(2x + 3)。

展开括号9x-3<4x + 6。

移项9x-4x<6 + 3，5x<9，解得x<(9)/(5)。