七年级数学SX福建省福州文博中学2011-2012学年七年级下学期数学第六单元测试试题
- 格式:pdf
- 大小:454.78 KB
- 文档页数:4

人教版七年级数学下册第六章实数单元综合能力提高测试卷一、选择题( 每题 3 分,共30分)1.以下选项中正确的选项是()A. 27的立方根是± 3B.16 的平方根是± 4C. 9 的算术平方根是3D.立方根等于平方根的数是12.在实数﹣ 0.8, 2015 ,﹣223),四个数中,是无理数的是(73A .﹣ 0.8B. 2015223 C.﹣D.733.( -1)2的平方根是()51B. -111A.25C.D.±25554.以下四个数中的负数是()A.﹣ 22B.( 1)2C.(﹣ 2)2D. |﹣2| 5. | 6 -3|+|2- 6 |的值为()A . 5B. 5-2 6C.1D. 2 6 -16.在以下各式中正确的选项是().( 2)2=-2.9=3.16=8.22=2A B C D 7.一个自然数 a 的算术平方根为x,则 a+1 的立方根是().3x 1B .3( x 1)2.3 a21D.3 x21A C8.以下结论中正确的个数为()( 1)零是绝对值最小的实数;( 2)数轴上全部的点都表示实数;( 3)无理数就是带根号的数;(4)-1的立方根为±1;273A.1 个B.2 个C.3 个D.4个9.若x 3 =3,则(x+3)2的值是()A. 81B. 27C. 9D. 310.如有理数 a 和 b 在数轴上所表示的点分别在原点的右侧和左侧,则b2-︱ a- b︱等于()A. a B.- a C. 2b+ a D.2b -a二、填空 (每小 3分,共30 分)11.在以下各数中无理数有个。
3 2 ,1,7, -, -3, 2 ,20, -5,38,25, 0, 0.5757757775 ⋯⋯6239(相两个 5 之的7 的个数逐次加1).12.一个数的算平方根等于它自己,个数是__________。
13.假如 x-4 是 16 的算平方根,那么x+ 4 的 ________.14.比大小:103;15.若25.36 =5.036,253.6 =15.906,253600= __________。

人教版七年级下册数学第6章实数培优试题一.选择题(共10小题)1.289的平方根是±17的数学表达式是()A=17 B=±17 C.=±17 D.=172则这个数的立方是()A.8 B.64 C.8或-8 D.64或-643.一个数的算术平方根是0.01,则这个数是()A.0.1 B.0.01 C.0.001 D.0.00014.下列各式中正确的是()A±4 B=-9 C D=3 25.如果-b是a的立方根,则下列结论正确的是()A.3b-=a B.-b=3a C.b=3a D.3b=a 6.已知正方体的体积为64,则这个正方体的棱长为()A.4 B.8 C.D.7.已知一个正数的两个平方根分别为3a-1和-5-a,则这个正数的立方根是()A.-2 B.2 C.3 D.48.在这四个数中,最小的数是()A.-2 B.0 C.1 D9)A.线段AB上B.线段BC上C.线段CD上D.线段DE上10.下列说法正确的是()A,则a>0B.若a与b也互为相反数C2,则a=bD.若a>b>0,b>二.填空题(共6小题)11.已知2x-1的平方根是±3,则5x+2的立方根是.12.若一个数的算术平方根与它的立方根相等,那么这个数是13.如图,某计算机中有、、三个按键,以下是这三个按键的功能.(1):将荧幕显示的数变成它的算术平方根,例如:荧幕显示的数为49时,按下后会变成7.(2):将荧幕显示的数变成它的倒数,例如:荧幕显示的数为25时,按下后会变成0.04.(3):将荧幕显示的数变成它的平方,例如:荧幕显示的数为6时,按下后会变成36.若荧幕显示的数为100时,小刘第一下按,第二下按,第三下按,之后以、、的顺序轮流按,则当他按了第2018下后荧幕显示的数是25x=4,则x的值为.14.对于正实数a,b作新定义:a⊙若215.已知实数a、b都是比2小的数,其中a是整数,b是无理数,请根据要求,分别写出一个a、b的值:a= ,b= .16.如图,长方形内有两个相邻的正方形,面积分别为4和3,那么阴影部分的面积为.三.解答题(共8小题)17.求x的值:(1)(x+1)2=64(2)8x3+27=0.1819.已知a+1的算术平方根是1,-27的立方根是b-12,c-3的平方根是±2,求a+b+c的平方根.20.如图所示的圆柱形容器的容积为81升,它的底面直径是高的2倍.(π取3)(1)这个圆柱形容器的底面直径为多少分米?(2)若这个圆柱形容器的两个底面与侧面都是用铁皮制作的,则制作这个圆柱形容器需要铁皮多少平方分米?(不计损耗)21.对于实数a、b定义运算"#"a#b=ab-a-1.(1)求(-2)#3的值;(2)通过计算比较3#(-2)与(-2)#3的大小关系;(3)若x#(-4)=9,求x的值.22.已知表示a,b两个实数的点在数轴上的位置如图所示,化简|a-b|+|a+b|.23.右图是一个无理数筛选器的工作流程图.(1)当x为16时,y值为(2)是否存在输入有意义的x值后,却始终输不出y值?如果存在,写出所有满足要求的x值;如果不存在,请说明理由;(3)如果输入x值后,筛选器的屏幕显示“该操作无法运行”,请你分析输入的x值可能是什么情况;(4)当输出的y时,判断输入的x值是否人教版七年级下册数学单元检测卷:第六章实数一、填空题(每小题4分,共20分)1.比较大小:3-2>-23(填“>”“<”或“=”).2.计算:9-14+38-|-2|=.3.3-5的相反数为,4-17的绝对值为,绝对值为327的数为.4.用“*”表示一种新运算:对于任意正实数a,b,都有a*b=b+1,例如8*9=+1=4,那么15*196= .5.观察分析下列数据,寻找规律:0,3,6,3,12,15,18,…,那么第13个数据是.二、选择题(每小题3分,共30分)6.-3的绝对值是()A.33B.-33C. 3 D.1 37.在实数-227,9,π,38中,是无理数的是()A.-227B.9C.πD.3 88.下列四个数中,最大的一个数是() A.2 B. 3 C.0 D.-29.某正数的平方根为a5和4a-255,则这个数为()A.1 B.2C.4 D.910.下面实数比较大小正确的是()A.3>7 B.3> 2C.0<-2 D.22<311.实数a在数轴上的位置如图1所示,则下列说法不正确的是()图1A.a的相反数大于2 B.a的相反数是2C.|a|>2 D.2a<012.如图2,在数轴上点A表示的数为3,点B表示的数为6.2,点A,B 之间表示整数的点共有()图2A.3个B.4个C.5个D.6个13.|5-6|=()A.5+ 6 B.5- 6C.-5- 6 D.6- 514.若x-1+(y+1)2=0,则x-y的值为()A.-1 B.1C.2 D.315. 已知3≈1.732,30≈5.477,那么300 000≈()A.173.2 B.±173.2C.547.7 D.±547.7 三、解答题(共70分)16.(6分)求下列各式的值.(1)252-242×32+42;(2)2014-130.36-15×900;(3)|a-π|+|2-a|(2<a<π).(精确到0.01)17.(8分)求下列各式中x的值.(1)x2-5=4;(2)(x-2)3=-0.125.18.(8分)已知实数a,b满足a-14+|2b+1|=0,求b a的值.19.(8分)芳芳同学手中有一块长方形纸板和一块正方形纸板,其中长方形纸板的长为3 dm,宽为2 dm,且两块纸板的面积相等.(1)求正方形纸板的边长(结果保留根号).(2)芳芳能否在长方形纸板上截出两个完整的,且面积分别为2 dm2和3 dm2的正方形纸板?判断并说明理由.(提示:2≈1.414,3≈1.732)20.(8分)已知x-2的平方根是±2,2x+y+7的立方根是3,求x2+y2的平方根.21.(10分)“欲穷千里目,更上一层楼”说的是登得高看得远,如图3,若观测点的高度为h,观测者视线能达到的最远距离为d,则d=2hR,其中R是地球半径(通常取6 400 km).小丽站在海边一块岩石上,眼睛离海平面的高度h 为20 m,她观测到远处一艘船刚露出海平面,求此时d的值.22.(1人教版七年级数学下册章末质量评估第六章实数人教版七年级数学下册第六章实数单元检测卷一、选择题1.若一个数的算术平方根等于它的相反数,则这个数是( D )A.0 B.1C.0或1 D.0或±12.下列各式成立的是( C )A. =-1B. =±1C. =-1D. =±13.与最接近的整数是( B )A.0 B.2 C.4 D.54..若x-3是4的平方根,则x的值为( C )A.2 B.±2 C.1或5 D.165.下列说法中,正确的个数有( A )①两个无理数的和是无理数;②两个无理数的积是有理数;③无理数与有理数的和是无理数;④有理数除以无理数的商是无理数.A.1个 B.2个 C.3个 D.4个B.的平方根是±4A.6.69 B.6.7 C.6.70 D.±6.708.一个底面是正方形的水池,容积是11.52m3,池深2m,则水池底边长是( C )A.9.25m B.13.52m C.2.4m D.4.2m9. 比较2, , 的大小,正确的是(C )A. 2< <B. 2< <C. <2<D. < <210.如果一个实数的算术平方根等于它的立方根,那么满足条件的实数有(C)A.0个B.1个om]C.2个D.3个二、填空题11.3的算术平方根是____3____.12.(1)一个正方体的体积是216cm 3,则这个正方体的棱长是____6________cm ;(2)表示_______9_____的立方根;13.已知a ,b 为两个连续整数,且a<15<b ,则a +b 的值为 7 . 14.已知一个有理数的平方根和立方根相同,则这个数是______0______.15.实数1-216.写出39到23之间的所有整数:____3,4 15.0________. 三、解答题17.求下列各数的平方根和算术平方根:(1)1.44;解:1.44的平方根是± 1.44=±1.2,算术平方根是 1.44=1.2. (2)169289; 解:169289的平方根是±169289=±1317,算术平方根是169289=1317.(3)(-911)2.解:(-911)2的平方根是±(-911)2=±911,算术平方根是(-911)2=911.[] 18.已知一个正数x 的两个平方根分别是3-5m 和m -7,求这个正数x 的立方根. 由已知得(3-5m)+(m -7)=0,-4m -4=0, 解得:m=-1.所以3-5m=8,m -7=-8. 所以x=(±8)2=64. 所以x 的立方根是4. 19.计算:(1)2+3 2-5 2;(2)2(7-1)+7;(3)0.36×4121÷318;(4)|3-2|+|3-2|-|2-1|;(5)1-0.64-3-8+425-|7-3|.解:(1)原式=(1+3-5)×2=- 2.(2)2(7-1)+7=2 7-2+7=3 7-2.(3)原式=0.6×211÷12。

一、选择题 1.若227(7)0x y z -+++-=,则x y z -+的平方根为( ) A .±2B .4C .2D .±4 2.在实数:20192020,π,9,3,2π,38,0.36,0.3737737773…(相邻两个3之间7的个数逐次加1),52-,49中,无理数的个数为( ) A .4B .5C .6D .7 3.若2x -+|y+1|=0,则x+y 的值为( ) A .-3B .3C .-1D .1 4.下列各式计算正确的是( ) A .31-=-1 B .38= ±2 C .4= ±2 D .±9=3 5.64的算术平方根是( )A .8B .±8C .22D .22± 6.如图,数轴上表示实数5的点可能是( )A .点PB .点QC .点RD .点S7.各个数位上数字的立方和等于其本身的三位数叫做“水仙花数”.例如153是“水仙花数”,因为333153153++=.以下四个数中是“水仙花数”的是( )A .135B .220C .345D .4078.在0.010010001,3.14,π,10,1.51,27中无理数的个数是( ). A .5个 B .4个 C .3 D .2个9.85-的整数部分是( )A .4B .5C .6D .710.下列选项中,属于无理数的是( )A .πB .227-C .4D .0 11.我们定义新运算如下:当m n ≥时,m 22n m n =-;当m n <时,m 3n m n =-.若5x =,则(3-)(6x -)x 的值为( ) A .-27B .-47C .-58D .-68 12.30.31,3π,27-912-38,1.212212221…(每两个1之间依次多一个2)中,无理数的个数为( )A .1B .2C .3D .413.在1.414,3-,213,5π,23-中,无理数的个数是( ) A .1 B .2C .3D .4 14.已知下列结论:①在数轴上不能表示无理数2;②无理数是无限小数;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是( ) A .① ③B .②③C .③④D .②④ 15.下列等式成立的是( )A .1±=±1B .4=±2C .3216-=6D .39=3 二、填空题16.如图,一只蚂蚁从点A 沿数轴向右爬了2个单位长度到达点B ,点A 表示2-,设点B 所表示的数为m .(1)实数m 的值是___________; (2)求|1||1|m m ++-的值;(3)在数轴上还有C 、D 两点分别表示实数c 和d ,且有|2|c d +与4d +互为相反数,求23c d -的平方根.17.先化简,再求值:()222233a ab a ab ⎛⎫---⎪⎝⎭,其中|2|a +3b - 18.求下列各式中x 的值(1)()328x -=(2)21(3)753x -=19.计算.(1)()113122⎛⎫⎛⎫---++ ⎪ ⎪⎝⎭⎝⎭; (2)()3328864---20.计算.(1)3218433⎛⎫-⨯-+- ⎪⎝⎭(2)178(4)4(5)-÷-+⨯-(3311256273⎫--⎪⎪⎭(4)22323223⎡⎤⎛⎫-⨯-⨯--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 21.如图所示,直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A 点,则A 点表示的数是_____.若点B 表示 3.14-,则点B 在点A 的______边(填“左”或“右”).22.如图,数轴上表示1和2的对应点分别为A B 、,点B 是AC 的中点,O 为原点.则线段长度:AB =__________,AC =__________,OC =____________23.8的相反数是_______,平方得9的数是________.24.在下列各数中,无理数有_______个.331320252,7,,2,,5,8,,0,0.57577577756239π--(相邻两个5之间的7的个数逐次加1). 25.若()221210a b c -+-=,则a b c ++=__________.26.已知a 是56的整数部分,b 是56的小数部分.则2=ab _____.三、解答题27.213a -=,31a b -+的平方根是4±,c 433a b c ++的平方根.28.定义一种新运算,观察下列式子:212122128=⨯+⨯⨯=★;2232322330=⨯+⨯⨯=★;()()()221212212-=⨯-+⨯⨯-=-★; ()()213132133-=-⨯+⨯-⨯=★;;(1)计算:()32-★的值;(2)猜想:a b =★________; (3)若12162a +=-★,求a 的值. 29.求满足条件的x 值: (1)()23112x -=x-=(2)2352-30.(2。

人教版七年级数学下册第六章实数素质检测卷一.选择题(共10 小题)1.4的值是()A.2B. -2C.± 2D.42.算术平方根等于它相反数的数是()A.0B.1C.0 或 1D.0 或± 13.以下实数是无理数的是()1A. -2B.πC.3D.164.以下说法正确的选项是()A.16 的平方根是 4B.8 的立方根是± 2C. -27 的立方根是 -3D.49 =±75.若3x3 y =0,则x与y的关系是()A. x=y=0B. x=yC. x 与 y 互为相反数D. x 与 y 互为倒数16 的平方根之和是()6.-64的立方根与A.0B. -6C. -2D.-6 或 -27.在实数中,立方根等于它自己的数有()A.1 个B.2 个C.3 个D.无数个8.绝对值大于不大于 6的整数有 ()个.A.5B. 10C. 6D. 139.关于非零的两个实数 a,b,规定 a※b=am –bn.若 3※ (–5)=15, (–1)※ 2 = –13,则 4※ (–7)的值为()A.?28B.28C. ?2D.210.如图,数轴上的点A,B,C,D,E对应的数分别为-1,0,1,2,3,那么与实数11 2 对应的点在()A.线段 AB 上B.线段 BC上C.线段 CD上D.线段 DE 上二.填空题(共 6 小题)11. 9 的平方根是; 的立方根是 .12.有一个数值变换器,原理如图:当输入的 x=4 时,输出的 y 等于.13.小于5 的最大整数是.14.数轴上从左到右挨次有A 、B 、C 三点表示的数分别为a 、b 、 10, 此中 b 为整数,且满足|a+3|+|b-2|=b-2, 则 b-a= .15.已知 |a|= 4, 3 b=2,ab<0,则a b 的值为.16.将一组数 按下边的方式进行摆列:2,2, 6,2 2, 10;2 3, 14,4,32,2 5;若 2 2 的地点记为(1,4), 26 的地点记为(3,3),则这组数中最大的有理数的地点记为.三.解答题(共 6 小题)4 |364| ( 3)23 12517.计算:27918.求以下各式中 x 的值:(1)(x+2)2-36=0;(2)64(x+1)3=27.19.已知 a 的平方根是它自己, b 是 2a+8 的立方根,求 ab+b 的算术平方根.20.已知5a1b 1 =0,求a2017(a b )2018的值.21.小丽想在一块面积为 640 cm2的正方形纸片中,沿着边的方向裁出一块面积为420 cm2的长方形的纸片,使它的长与宽之比为3:2,小丽能用这块纸片裁出切合要求的纸片吗?请简要说明原因.22.如图,面积为30 的长方形OABC的边 OA 在数轴上, O 为原点, OC=5,将长方形OABC 沿数轴水平挪动 ,O,A,B,C 挪动后的对应点分别记为O,A, B , C ,挪动后的长方形OABC 与11111111原长方形 OABC重叠部分的面积记为S.(1)当 S恰巧等于原长方形面积的一半时,数轴上点A1表示的数是多少?(2)设点 A 的挪动距离AA=x.1①当 S=10 时,求 x 的值;D1E1OE=1OO,D E②为线段 AA 的中点,点在线段 OO上,且当点所表示的数互为相反数31,时,求 x 的值.1-5AABCC6-10 DCBBC11.人教版七年级下册第六章实数单元能力检测卷人教版七年级数学下册第六章实数单元检测卷1.若,则 a 的值为 ()A.B.C. 4D.±4 2.以下各对数是互为相反数的是()A.–2与 0.5B.与C.与D.与3.若x,y为实数,且|x+1|+=0,则的值是()A.0B. 1C.- 1D.- 2011 4.有一个数的相反数、平方根、立方根都等于它自己,这个数是() A.- 1B. 1C. 0D.±1 5.若与的整数部分分别为,则的立方根是 () A.B.C. 3D.6.有一个数值变换器,原理如下图 .当输入的x 为 -512时 ,输出的 y 是()A.-2B.-C.-D.-7.计算的结果预计在()A.4至5之间B.5至6之间C.6至7之间D.4至 6之间8.在-,0,-2,1,-1这五个数中,最大的数和最小的数的和是()B.-C.- 2D.- 19.如图,以数轴的单位长度线段为边作一个正方形,以表示数 2 的点为圆心、正方形对角线的长为半径画弧,交数轴于点A,则点 A 表示的数是 ()A.-B. 2-C. 1-D. 1+10.规定新运算a* b= ab- (a+ b),若 (-3)* x=3,则 x 的值是 ()A.0B. 1C. 2D.- 1二、填空题11.若a是4的平方根,b=-42,那么a+b的值为___ _____.12.小明的寝室面积为18 m2,他数了一下地面所铺的正方形地板砖恰巧是200 块,则每块地板砖的边长为 ___ _____m.213.若│x-16│+=0,则 x+ y= __ ___.14.若x-1是125的立方根,则x- 7 的立方根是 __ ____.15.用适合的符号填空:若b> c> 0,则 b﹣c_ _0, | c﹣ b|_ _0 ,_ _0.16.察看以下算式:①=+=16+4=20;②=+=40+4=44;③=+=72+4=76;④=+=112+4=116;⋯依据以上律算:=___ _______.三、解答未命名17.算:-+||+.18.求以下各式中的.(1)(2).19.如,数a、b 在数上的地点,化.20.小明家装饰用了大小同样的正方形瓷共66 成10.56 米2的房,小明想知道每瓷的,你帮助算一算.21.数学老在堂上提出一个:“通研究知道:≈ 1.414,⋯它是个无穷不循小数,也叫无理数,它的整数部分是1,那么有谁能说出它的小数部分是多少”,小明举手回答:它的小数部分我们没法所有写出来,但能够用﹣1来表示它的小数部分,张老师夸耀小明真聪慧,一定了他的说法.现请你依据小明的说法解答:(1)的小数部分是 a,的整数部分是b,求 a+b﹣的值.(2)已知 8+ =x+y,此中 x 是一个整数, 0< y<1,求 3x+( y﹣)2018的值.22.已知a是最大的负整数,b是多项式2m2n﹣m3n2﹣m﹣2的次数,c是单项式﹣2xy2的系数,且 a、 b、 c 分别是点 A、B、 C 在数轴上对应的数.(1)求(2)若a、 b、 c 的值,并在数轴上标出点M 点在此在此数轴上运动,恳求出A、 B、C.M 点到 AB 两点距离之和的最小值;(3)若动点 P、Q 同时从 A、B 出发沿数轴负方向运动,点P的速度是每秒个单位长度,点 Q 的速度是每秒 2 个单位长度,求运动几秒后,点 Q 能追上点(4)在数轴上找一点N,使点M 到A、B、C 三点的距离之和等于对应的数.(不用说明原因)P?10,请直接写出所有的N参照答案:1.B2.B3.C4.C5.A6.D7.B8.D9.B10.A二、填空题11.-14或-1812.0.313.7或-114.-115.>,>,<16.4076356三、解答题未命名17.原式=7-3+-1+=+18.(1) x2=x= ±(2) 2x-9=-32x=6..x=3.19.解:由数轴知,a<0,且 b>0 , a-b<0,=│ a│-│ b│-[- ( a-b) ]=(-a) -b+a-b=-2b.20.解:设每块瓷砖的边长是x米,由题意得 66x2=10.56 ,x=0.4.每块瓷砖的边长是0.4米 .21.解:( 1)∵ 4<5<9 , 9<13<16 ,∴2< <3, 3<<4.∴a= -2, b=3.∴a+b- = -2+3-=1.(2)∵ 1<<2, .∴ 9<8+<10,∴x=9.∵y=8+-x.∴y- =8-x=-1∴原式 =3×9+1=28.22.(1)∵ a 是最大的负整数,∴a=-1 ,∵b是多项式 2m2n-m 3n 2.m-2 的次数,∴b=3+2=5,∵c是单项式 -2x2的系数,∴c=-2,如下图:(2)当 M 点在线段 AB 上时, M 点到 AB 两点距离之和的最小值为5-(-1) =6;(3):∵动点 P、Q 同时从 A、B 出发沿数轴负方向运动,点P的速度是每秒个单位长度,点 Q 的速度是每秒 2 个单位长度,∴AB=6,两点速度差为: 2—,∴6+( 2—) =4,答:运动 4 秒后,点Q 能够追上点P人教版七年级下册第六章实数单元同步测试一、选择题1、以下说法正确的选项是()A.负数没有立方根B.一个正数的立方根有两个,它们互为相反数C.假如一个数有立方根,则它必有平方根D. 不为 0 的任何数的立方根,都与这个数自己的符号同号2、以下语句中正确的选项是()A.-9 的平方根是 -3B.9 的平方根是 3C.9 的算术平方根是3D.9 的算术平方根是 33、以下说法中正确的选项是()A、若 a 为实数,则a0 B 、若 a 为实数,则 a 的倒数为1aC、若 x,y 为实数,且x=y ,则x y D 、若 a 为实数,则a204、估量287 的值在A. 7和8之间B. 6和 7之间C. 3和4之间D. 2和 3之间5、以下各组数中,不可以作为一个三角形的三边长的是()A、 1、 1000、 1000B、 2、 3、5C、32,42,52D、38 , 327 , 3646、以下说法中,正确的个数是()(1)- 64 的立方根是-4;( 2)49的算术平方根是7 ;(3)1的立方根为1;(4)1是1的平方根。
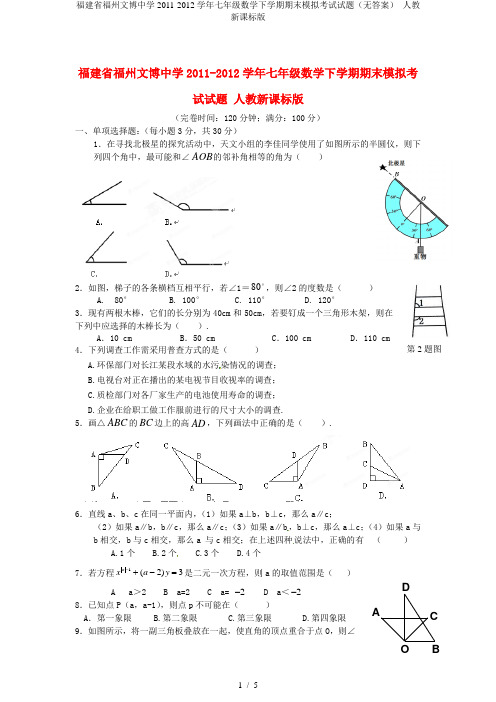
福建省福州文博中学2011-2012学年七年级数学下学期期末模拟考试试题 人教新课标版(完卷时间:120分钟;满分:100分)一、单项选择题:(每小题3分,共30分)1.在寻找北极星的探究活动中,天文小组的李佳同学使用了如图所示的半圆仪,则下列四个角中,最可能和∠AOB 的邻补角相等的角为( )2.如图,梯子的各条横档互相平行,若∠1=80,则∠2的度数是( )A. 80°B. 100°C. 110°D. 120°3.现有两根木棒,它们的长分别为40cm 和50cm ,若要钉成一个三角形木架,则在下列中应选择的木棒长为( ).A .10 cmB .50 cmC .100 cmD .110 cm4.下列调查工作需采用普查方式的是( ) A.环保部门对长江某段水域的水污染情况的调查; B.电视台对正在播出的某电视节目收视率的调查; C.质检部门对各厂家生产的电池使用寿命的调查;D.企业在给职工做工作服前进行的尺寸大小的调查.5.画△ABC 的BC 边上的高AD ,下列画法中正确的是( ).6.直线a 、b 、c 在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,那么a∥c;(3)如果a∥b ,b⊥c,那么a⊥c;(4)如果a 与b 相交,b 与c 相交,那么a 与c 相交;在上述四种说法中,正确的有 ( )A.1个B.2个C.3个D.4个 7.若方程1(2)3a xa y -+-=是二元一次方程,则a 的取值范围是( )A a >2B a=2C a= 2-D a <2-8.已知点P (a ,a-1),则点p 不可能在( )A .第一象限 B.第二象限 C.第三象限 D.第四象限 9.如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O ,则∠第2题图 OD C BA第18题图 D CB E A(第10题)AOB+∠DOC 的值为( )A 小于180°或等于180°B 等于180°C 小于180°D 大于180°或等于180°10.如图是由五个同样的三角形组成的正五边形图案,三角形的三个角分别为36°、 72°、 72°, 则图中平行线共有( )A .2对B .3对C .4对D .5对二、填空题:(每小题2分,共16分)11.已知点A (1,2),则A 点在第 象限. 12.已知x =2,y =3 满足方程2x +ky =13,则k =_______. 13.如图,∠A=100°,∠B=∠C,则∠B= .14.合用 和正三角形瓷砖可以进行地面密铺.(只需填写一种正多边形)15.如图,BD ∥AC ,点E 在线段AB 的延长线上,∠1=38°, ∠C=75°,则∠ABC 的度数是 .16.不等式组123x x -≤⎧⎨-<⎩的解集是 .17.请添加一个方程,使二元一次方程组4x y +=⎧⎪⎨⎪−−−⎩的解是⎩⎨⎧=-=51y x18.如图,在△ABC 中,∠B =∠C ,,且∠ADE =∠AED ,则∠CDE 的度数为 三、解答题:(本大题共54分) 19.(本题满分8分,每小题4分) (1)解下列方程组:① x -y=32x +y=21②3(x -1)=y +53(x +5) =5(y -1)20. 解下列不等式,并把解集在数轴上表示出来:(本题满分10分,每小题5分) (1)211,84 1.x x x x ->+⎧⎨+≤-⎩ (2)13554(4)3(6)x xx x+-⎧>⎪⎨⎪+<+⎩21.(7分)如图,直角坐标系中,△ABC 的顶点都在网格点上,其中,C 点坐标为(1 ,2), 出点A 、B 的坐标:A ( , )、B ( , )②将△ABC 先向左平移2个单位长度,再向上平移 1个单位长度,得到△A 'B 'C ',则A 'B 'C '的三个 顶点坐标分别是A '( , )、B '( , )、 C '( , )③△ABC 的面积为____________.(2分) 22.(本题10分)已知如图, DE ⊥AC , ∠AGF=∠ABC , ∠1+∠2=1800, 试判断BF 与AC 的位置关系, 并说明理由.23.(9分)为解决居民饮水问题,我县政府决定修一条总长为1800米的引水渠,并将工程承包给甲、乙两工程队来施工.若甲、乙两队合做10天后,再由甲单独完成剩下的工程刚好20天完成;若甲队先做了12天后,剩下的由乙队单独做还需40天才能完工. (1)问甲队、乙队每天各施工多少米工程?(4分)(2)已知甲队每施工一天需要费用3万元,乙队每施工一天需要费用1.5万元,要使完成该工程所需费用不超过100万元,则乙工程队至少要施工多少天?(5分)24.(本小题满分8分)小龙在学校组织的社会调查活动中负责了解他所居住的小区500户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.分组频数百分比600≤x<800 2 5%800≤x<1000 6 15%1000≤x<1200 45%1200≤x<1400 9 22.5%1400≤x<16001600≤x<1800 2合计40 100%根据以上提供的信息,解答下列问题:(1)补全频数分布表;(2)补全频数分布直方图;(3)请你估计该居民小区家庭属于中等收入(1000≤x<1600)的大约有多少户?25、(本小题满分10分)如图1,在△ABC中,AD为BC边上的高,AE为∠BAC的平分线,已知∠B=20°,∠C=50º(1)求∠EAD的度数;(2)你发现∠EAD与∠B、∠C之间有何关系?(3)若将“题中的条件∠B=20°”改为“∠B=100°”如图2,其它条件不变,则∠EAD 与∠B、∠C之间又有何关系?请说明理由。

福建省福州市文博中学2012-2013学年七年级下学期期末考试数学试题一、选择题(本题共10小题,1、如图,在所标识的角中,对顶角是(Y - 2 > 0_心的解集表示在数轴上,正融壯7、 为了了解1万桶仙泉矿泉水的质量,从中抽取了 50桶进行测试,下列叙述正确的是( )A . 1万桶仙泉矿泉水是总体B .每桶仙泉矿泉水是个体C . 50桶仙泉矿泉水的质量是总体的一个样本D .以上说法都不正确8、 将点A ( 4,— 2)向左平移3个单位长度得到点 B 的坐标是()A . ( 4, 1)B . ( 1 , -2)C . ( 7, -2 )D . (4, -5)9、 灾后重建,四川从悲壮走向豪迈,灾民发扬伟大的抗震救灾精神,桂花村派男女村民共15人到山外采购建房所需的水泥,已知男村民一人挑两包,女村民两人抬一包,共购 回15包,请问这次采购派男女村民各()人每小题2分,共20分)) D . Z 3和/42、4的平方根是( )A . 2B .2C .、3、 22 在 ,1.414 ,39 ,,2、• 3 , 9这些数中7A . 2个B . 3个C . 4个4、 下列方程中,是二兀 一次方程的有()A . 6x 2 5z16x1 B .-13x yC . xy 3x y1D . x 2yx 3 y的解是(5方程组)2x y 5x 3x 1x 2A .B .C .y 5 y2y1,无理数的个数是()加把不等式组I I-1 0A ./ 1 和/ 21和/ 3C .Z 2 和/ 4B . Z —1 0A .男村民3人,女村民12人B.男村民5人,女村民10人那么a i 与a 20i3的位置关系是( )二.填空题(本题共W 小题,每小题2分,共昭分》.工的2借与3的差不大于『用不等式表示为 __________ •~12.如图所示,请写出能利定直約/卜的一牛条件 __________________ ・学\1弘点血—1)和点◎ n )关于Y 轴对S 礼则吋等于 ______________ ・ /弟1建14.—个容量% 30的样本蟲走值光143,最小值対50,取组距矢16,则可康分成 __ 且 1%把命题用平行干同一直线的两直護平行'改写成^如果…….那么……妙的形式I口① 一个数的立方根的相反数等于这个数的相反数的立方根; ② 64的平方根是士 8,立方根是士 4;③j a a 0表示a 的平方根,Va 表示a 的立方根;④yfa 一定是负数。
一、选择题1.27(7)0y z ++-=,则x y z -+的平方根为( )A .±2B .4C .2D .±4D 解析:D【分析】根据绝对值,平方,二次根式的非负性求出x ,y ,z ,算出代数式的值计算即可;【详解】∵27(7)0y z ++-=,∴207070x y z -=⎧⎪+=⎨⎪-=⎩,解得277x y z =⎧⎪=-⎨⎪=⎩,∴()27716x y z -+=--+=,∴4=±;故选:D .【点睛】本题主要考查了平方根的求解,结合绝对值、二次根式的非负性计算是解题的关键. 2.下列说法中错误的有( )①实数和数轴上的点是一一对应的;②负数没有立方根;③算术平方根和立方根均等于其本身的数只有0;④49的平方根是7±7=±.A .0个B .1个C .2个D .3个D解析:D【分析】利用实数和数轴的关系,算术平方根,立方根及平方根定义判断即可.【详解】①实数和数轴上的点是一一对应的,正确;②负数有立方根,错误;③算术平方根和立方根均等于其本身的数有0和1,错误;④49的平方根是7±7=,错误.综上,错误的个数有3个.故选:D .本题考查了实数和数轴,平方根,算术平方根及立方根,熟练掌握各自的定义是解本题的关键.3.下列说法正确的是( )A .2-是4-的平方根B .2是()22-的算术平方根C .()22-的平方根是2D .8的平方根是4B 解析:B【分析】根据平方根、算术平方根,即可解答.【详解】A 选项:4-没有平方根,故A 错误;B 选项:()224-=,4的算术平方根为2,故B 正确;C 选项:()224-=,4的平方根为2±,故C 错误;D 选项:8的平方根为±,故D 错误故选B .【点睛】本题考查了平方根、算术平方根,解决本题的关键是熟记平方根、算术平方根的概念.4.0215中,是无理数的是( )A B .0 C D .215A 解析:A【分析】根据无理数是无限不循环小数,可得答案.【详解】,0215, 故选:A .【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.5.在0.010010001,3.14,π,1.51,27中无理数的个数是( ). A .5个B .4个C .3D .2个D解析:D【分析】 根据无理数的概念解题,找出无理数的个数即可,无限不循环小数称为无理数;在0.010010001,3.14,π,1.51,27中无理数有π共2个, 故选D .【点睛】本题考查了无理数的概念,正确掌握无理数的概念是解题的关键;6.81的平方根是( )A .9B .-9C .9和9-D .81C 解析:C【分析】根据平方根的定义即可求出答案.【详解】解:2(9)81±=, 81的平方根是9±.故选:C【点睛】本题考查平方根的定义,解题的关键是正确理解平方根的定义,本题属于基础题型.7.下列实数31,7π-,3.14,1.010010001…(从左到右,每两个1之间依次增加一个0)中,其中无理数有( )A .5个B .4个C .3个D .2个C 解析:C【分析】根据无理数的定义、算术平方根与立方根逐个判断即可得.【详解】31 4.4285717=小数点后的428571是无限循环的,属于有理数,3=-属于有理数,=则无理数为π-⋯,共有3个,故选:C .【点睛】本题考查了无理数、算术平方根与立方根,熟记各定义是解题关键.8.下列实数中,属于无理数的是( )A .3.14B .227CD .πD解析:D【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【详解】解:A 、3.14是小数,是有理数,故A 选项错误;B 、227是有限小数,是有理数,故B 选项错误;C =2是整数,是有理数,故C 选项错误.D 、π是无理数,故D 选项正确故选:D .【点睛】本题考查了无理数的定义,无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.9.和数轴上的点一一对应的数是( )A .自然数B .有理数C .无理数D .实数D解析:D【分析】根据实数与数轴上的点是一一对应关系,即可得出.【详解】解:根据实数与数轴上的点是一一对应关系.故选:D .【点睛】本题考查了实数与数轴的对应关系,任意一个实数都可以用数轴上的点表示;反之,数轴上的任意一个点都表示一个实数.10 )A .8B .8-C .D .± D 解析:D【分析】8=,再根据平方根的定义,即可解答.【详解】8=,8的平方根是±故选:D .【点睛】8=. 二、填空题11.已知一个正数的平方根是3a +和215a -.(1)求这个正数.(2)求12a +的平方根和立方根.(1)441或49;(2)或【分析】(1)分情况讨论这两个平方根相等或互为相反数求出a 的值在算出这个正数;(2)由(1)的结果分情况讨论根据平方根和立方根的定义算出结果【详解】解:(1)若这两个平方解析:(1)441或49;(2)30±,330或2±,34 【分析】(1)分情况讨论,这两个平方根相等或互为相反数,求出a 的值,在算出这个正数; (2)由(1)的结果分情况讨论,根据平方根和立方根的定义算出结果.【详解】解:(1)若这两个平方根相等,则3215a a +=-,解得18a =,这个正数是:()2218321441+==;若这两个平方根互为相反数,则32150a a ++-=,解得4a =,这个正数是:()2243749+==;(2)若18a =,则1230a +=,30的平方根是30±,立方根是330;若4a =,则12164a +==,4的平方根是2±,立方根是34.【点睛】本题考查平方根和立方根,解题的关键是掌握平方根和立方根的定义以及计算方法. 12.教材中的探究:如图,把两个边长为1的小正方形沿对角线剪开,用所得到的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法(数轴的单位长度为1).(1)阅读理解:图1中大正方形的边长为________,图2中点A 表示的数为________; (2)迁移应用:请你参照上面的方法,把5个小正方形按图3位置摆放,并将其进行裁剪,拼成一个大正方形.①请在图3中画出裁剪线,并在图3中画出所拼得的大正方形的示意图.②利用①中的成果,在图4的数轴上分别标出表示数-0.5以及 35-的点,并比较它们的大小.(1);(2)①见解析;②见解析【分析】(1)设正方形边长为a 根据正方形面积公式结合平方根的运算求出a 值则知结果;(2)①根据面积相等利用割补法裁剪后拼得如图所示的正方形;②由题(1)的原理得出大正 解析:(1)2,2-;(2)①见解析;②见解析, 350.5-+<-【分析】(1)设正方形边长为a ,根据正方形面积公式,结合平方根的运算求出a 值,则知结果; (2) ① 根据面积相等,利用割补法裁剪后拼得如图所示的正方形;②由题(1)的原理得出大正方形的边长为5,然后在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M ,再把N 点表示出来,即可比较它们的大小.【详解】解:设正方形边长为a ,∵a 2=2,∴a=2±,故答案为:2,2-;(2)解:①裁剪后拼得的大正方形如图所示:②设拼成的大正方形的边长为b ,∴b 2=5,∴b=±5,在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M ,则M 表示的数为-3+5,看图可知,表示-0.5的N 点在M 点的右方,∴比较大小:350.5-+<-.【点睛】本题主要考查平方根与算术平方根的应用及实数的大小比较,熟练掌握平方根与算术平方根的意义及实数的大小比较是解题的关键.13.计算:(1.(2)()23540.255(4)8⨯--⨯⨯-.(1)6;(2)【分析】(1)首先计算算术平方根立方根然后进行加减计算即可;(2)首先计算乘方乘法最后进行加减计算即可【详解】解:(1)=4-(-2)=6(2)===【点睛】本题考查了实数的混合运算 解析:(1)6;(2)70.【分析】(1)首先计算算术平方根、立方根,然后进行加减计算即可;(2)首先计算乘方、乘法,最后进行加减计算即可.【详解】解:(1=4-(-2)=6.(2)()23540.255(4)8⨯--⨯⨯- =()()5160.255648⨯--⨯⨯-=1080-+=70.【点睛】 本题考查了实数的混合运算,正确理解算术平方根、立方根性质及乘方法则,确定运算顺序是关键.14.计算:(1)225--(2)1+(1)-4;(2)1【分析】(1)根据乘方开方绝对值的意义化简再计算即可;(2)先根据绝对值的意义脱去绝对值再计算即可求解【详解】解:(1)=-4+6-1-5=-4;(2)=-1+2=1【点睛】本题解析:(1)-4;(2)1.【分析】(1)根据乘方、开方、绝对值的意义化简,再计算即可;(2)先根据绝对值的意义脱去绝对值,再计算即可求解.【详解】解:(1)225--=-4+6-1-5=-4;(2)1)1=++1=+1=-+=-1+2=1.【点睛】本题考查了实数的性质与运算,熟知实数的运算法则和性质是解题关键.15.()220y -=,则xy =_________.-1【分析】由非负数的性质可知x=-y=2然后求得xy 的值即可【详解】解:∵|+(y-2)2=0∴2x+1=0y-2=0∴x=-y=2∴xy=-×2=-1故答案为:-1【点睛】本题考查了非负数的性质解析:-1【分析】由非负数的性质可知x=-12,y=2,然后求得xy 的值即可. 【详解】解:∵(y-2)2=0,∴2x+1=0,y-2=0, ∴x=-12,y=2. ∴xy=-12×2=-1. 故答案为:-1.【点睛】本题考查了非负数的性质,掌握非负数的性质是解题的关键.16.若2x =,29y =,且0xy <,则x y -等于______.5或-5【分析】先由绝对值和平方根的定义求得xy 的值然后根据xy <0分类计算即可;【详解】∵∴∵xy <0∴当x=2y=-3时x-y=2+3=5当x=-2y=3时x-y=-2-3=-5故答案为:5或- 解析:5或-5【分析】先由绝对值和平方根的定义求得x 、y 的值,然后根据xy <0分类计算即可;【详解】∵ 2x =,29y =,∴ 2x =±,3=±y ,∵ xy <0,∴ 当x=2,y=-3时,x-y=2+3=5,当x=-2,y=3时,x-y=-2-3=-5,故答案为:5或-5【点睛】本题主要考查了平方根的定义、绝对值、有理数的减法,正确掌握知识点是解题的关键; 17.阅读下列信息材料信息1:因为尤理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来比如:π“……”或者“≈”的表示方法都不够百分百准确;信息2:2.5的整数部分是2,小数部分是0.5,可以看成2.52-得来的;信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如23<<,是因为<;根据上述信息,回答下列问题:(1___________,小数部分是______________;(2)若2122a <<,则a 的整数部分是___________;小数部分可以表示为_______;(3)10+10a b <则a b +=______;(43x y =+,其中x 是整数,且01y <<,请求x y -的相反数.(1)3;;(2)21;;(3)23;(4)【分析】(1)先找到可找到即可找出的整数部分与小数部分(2)根据因为即可找出的整数部分与小数部分(3)找到在哪两个整数之间再加10即可(4)先确定找到由是解析:(1)33;(2)21;21a -;(3)23;(47.【分析】(1)先找到91316<<,可找到34<< (2)根据因为2122a <<,即可找出a 的整数部分与小数部分(3)找到12<<在哪两个整数之间,再加10即可.(4)先确定56<<,找到233<<,由01y <<,x 是整数,即可确定x=2,5,再求7x y -=,即可求出【详解】(1)91316<< ∴34<<33故答案为:33;(2)因为2122a <<,故则a 的整数部分是21,a 的小数部分可以表示为21a -. 故答案为:21;21a -;(3)因为12<<,∴10110102+<+<+,即111012<+<,所以=11a ,=12b ,故23a b +=,故答案为:23;(4)5306<<,23033<<,∵01y <<,x 是整数,∴x=2, ∴325-=,∴)257x y -=-=, ∴x y -7.【点睛】本题考查的是无理数的整数部分与小数部分,掌握估值法确定无理数的范围,即无限不循环小数知识的拓展延伸,理解题意,按照题目所给的表示方法去解答是关键.18.定义运算“@”的运算法则为:,则2@6 =____.4【分析】把x=2y=6代入x@y=中计算即可【详解】解:∵x@y=∴2@6==4故答案为4【点睛】本题考查了有理数的运算能力注意能由代数式转化成有理数计算的式子解析:4【分析】把x=2,y=6代入中计算即可.【详解】解:∵, ∴=,故答案为4.【点睛】本题考查了有理数的运算能力,注意能由代数式转化成有理数计算的式子.19.比较大小:12___________12<【分析】利用作差法比较两个数的大小【详解】解:∵1<3<4∴1<<2∴1-1<-1<2-1∴0<-1<1∴<故答案为:<【点睛】本题考查了实数的大小比较此题的难点是利用夹逼法推知的取值范围 解析:<【分析】利用作差法比较两个数的大小.【详解】解:∵1<3<4∴1<2∴1-1<2-1∴0<1∴12<12.故答案为:<.【点睛】本题考查了实数的大小比较,此题的难点是利用“夹逼法”20.已知1a-的平方根是2±,则a的值为_______.5【分析】根据平方根的定义求解即可【详解】的平方根是a-1=4a=5故答案为:5【点睛】此题考查了平方根的定义一个整数的平方根有两个它们互为相反数解析:5【分析】根据平方根的定义求解即可.【详解】1a-的平方根是2±,∴a-1=4,∴a=5.故答案为:5【点睛】此题考查了平方根的定义,一个整数的平方根有两个,它们互为相反数.三、解答题21.一个四位正整数的千位、百位、十位、个位上的数字分别为a,b,c,d,如果a b c d≤≤≤,那么我们把这个四位正整数叫做进步数,例如四位正整数2347:因为2347<<<,所以2347叫做进步数.(1)求四位正整数中的最大的“进步数”与最小的“进步数”的差;(2)已知一个四位正整数的百位、个位上的数字分别是1、4,且这个四位正整数是“进步数”,同时,这个四位正整数能被7整除,求这个四位正整数.解析:(1)8888;(2)1134 .【分析】(1)根据进步数的定义分别求出四位正整数中的最大“进步数”与最小“进步数”即可得解;(2)根据进步数的定义可以推得所求数为1114、1124、1134、1144中的某一个,再根据这个四位正整数能被7整除逐一对4个数进行验证可以得解.【详解】解:(1)由进步数的定义可知四位正整数中最大的“进步数”应该是9999,又最高位不能为0,所以四位正整数中的千位最小为0,所以四位正整数中最小的“进步数”应该是1111,∴9999-1111=8888,∴四位正整数中的最大的“进步数”与最小的“进步数”的差为8888;(2)由已知可得所求数的千位为1,十位为1-4中的某个数字,∴所求数为1114、1124、1134、1144中的某一个,∵这个四位正整数能被7整除,∴由1114=159×7+1,1124=160×7+4,1134=162×7,1144=163×7+3可知所求数为1134 .【点睛】本题考查新定义下的实数规律探索,由材料归纳出新定义并应用于具体问题求解是解题关键.22.求下列各式中的x :(1)29(1)25x -=(2)3548x +=解析:(1)x=83或x=-23;(2)x =32-. 【分析】 (1)根据平方根的定义解答即可;(2)根据立方根的定义解答即可.【详解】解:(1)∵9(x-1)2=25∴x-1=±53, 即x-1=53或x-1=-53, 解得x=83或x=-23; (2)3548x += 3548x =- 3278x =-x =32-. 【点睛】本题主要考查了求一个数的平方根与立方根,熟记定义是解答本题的关键.23.阅读下列信息材料信息1:因为尤理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来比如:π“……”或者“≈”的表示方法都不够百分百准确;信息2:2.5的整数部分是2,小数部分是0.5,可以看成2.52-得来的;信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如23<<,是因为<;根据上述信息,回答下列问题:(1___________,小数部分是______________;(2)若2122a <<,则a 的整数部分是___________;小数部分可以表示为_______;(3)10+10a b <则a b +=______;(43x y =+,其中x 是整数,且01y <<,请求x y -的相反数.解析:(1)33;(2)21;21a -;(3)23;(47.【分析】(1)先找到91316<<,可找到34<< (2)根据因为2122a <<,即可找出a 的整数部分与小数部分(3)找到12<<在哪两个整数之间,再加10即可.(4)先确定56<<,找到233<<,由01y <<,x 是整数,即可确定x=2,5,再求7x y -=,即可求出【详解】(1)91316<< ∴34<<33故答案为:33;(2)因为2122a <<,故则a 的整数部分是21,a 的小数部分可以表示为21a -. 故答案为:21;21a -;(3)因为12<<, ∴10110102+<+<+,即111012<+<,所以=11a ,=12b ,故23a b +=,故答案为:23;(4)5306<<,23033<<,∵01y <<,x 是整数,∴x=2, ∴325-=,∴)257x y -=-=,∴x y -7.【点睛】本题考查的是无理数的整数部分与小数部分,掌握估值法确定无理数的范围,即无限不循环小数知识的拓展延伸,理解题意,按照题目所给的表示方法去解答是关键.24.已知一个正数的平方根是3a +和215a -.(1)求这个正数.(2的平方根和立方根.解析:(1)441或49;(2)2± 【分析】(1)分情况讨论,这两个平方根相等或互为相反数,求出a 的值,在算出这个正数; (2)由(1)的结果分情况讨论,根据平方根和立方根的定义算出结果.【详解】解:(1)若这两个平方根相等,则3215a a +=-,解得18a =,这个正数是:()2218321441+==;若这两个平方根互为相反数,则32150a a ++-=,解得4a =,这个正数是:()2243749+==;(2)若18a ==若4a =4==,4的平方根是2±.【点睛】本题考查平方根和立方根,解题的关键是掌握平方根和立方根的定义以及计算方法.25.1-+.解析:1【分析】先根据开方的意义,绝对值的意义进行化简,最后计算即可求解.【详解】解:原式123122=-+++⨯1=+ 【点睛】本题考查了实数的混合运算,理解开方的意义,能正确去绝对值是解题关键. 26.已知一个正数m 的平方根为2n +1和4﹣3n .(1)求m 的值;(2)|a ﹣3|(c ﹣n )2=0,a +b +c 的立方根是多少?解析:(1)m =121;(2)a +b +c 的立方根是2【分析】(1)由正数的平方根互为相反数,可得2n +1+4﹣3n =0,可求n =5,即可求m ; (2)由已知可得a =3,b =0,c =n =5,则可求解.【详解】解:(1)正数m 的平方根互为相反数,∴2n +1+4﹣3n =0,∴n =5,∴2n +1=11,∴m =121;(2)∵|a ﹣3|(c ﹣n )2=0,∴a =3,b =0,c =n =5,∴a +b +c =3+0+5=8,∴a +b +c 的立方根是2.【点睛】本题考查平方根的性质;熟练掌握正数的平方根的特点,绝对值和偶次方根数的性质是解题的关键.27.观察下列各式:322111124==⨯⨯,33221129234+==⨯⨯,33322112336344++==⨯⨯,33332211234100454+++==⨯⨯;… 回答下面的问题:(1)猜想:33333123(1)n n ++++-+=_________;(直接写出你的结果)(2)根据(1)中的结论,直接写出13+23+33+......+93+103的值是_________; (3)计算:213+223+233+......+293+303的值.解析:(1)221(1)4n n ⨯⨯+;(2)3025;(3)172125【分析】(1)根据题中所给各式可直接进行分析求解;(2)由(1)可直接代入求值即可;(3)根据(1)可直接进行求解.【详解】解:(1)根据题意可得出:33333123(1)n n ++++-+=221(1)4n n ⨯⨯+; (2)将n =10代入221(1)4n n ⨯⨯+, 原式221×1010130254=⨯+=();(3)原式=22221130(301)20(201)44⨯⨯+-⨯⨯+=172125.【点睛】本题主要考查实数的运算,熟练掌握实数的运算是解题的关键. 28.求满足下列条件的x 的值:(1)3(3)27x +=-; (2)2(1)218x -+=.解析:(1)6x =-;(2)3x =-或5【分析】(1)根据立方根,即可解答;(2)根据平方根,即可解答.【详解】解:(1)3(3)27x +=-33x +=-6x =-;(2)2(1)218x -+=2(1)16x -=14x -=±∴3x =-或5.【点睛】本题考查了平方根、立方根,解决本题的关键是熟记平方根、立方根的定义.。
人教版七年级下册 第六章 实数 单元同步测试一、选择题1、下列说法正确的是( ) A.负数没有立方根B.一个正数的立方根有两个,它们互为相反数C.如果一个数有立方根,则它必有平方根D.不为0的任何数的立方根,都与这个数本身的符号同号 2、下列语句中正确的是( )A.-9的平方根是-3B.9的平方根是3C.9的算术平方根是3±D.9的算术平方根是3 3、下列说法中正确的是( )A 、若a 为实数,则0≥aB 、若a 为实数,则a 的倒数为a1 C 、若x,y 为实数,且x=y ,则y x = D 、若a 为实数,则02≥a4、估算728-的值在A. 7和8之间B. 6和7之间C. 3和4之间D. 2和3之间 5、下列各组数中,不能作为一个三角形的三边长的是( )A 、1、1000、1000B 、2、3、5C 、2225,4,3 D 、38,327,3646、下列说法中,正确的个数是( )(1)-64的立方根是-4;(2)49的算术平方根是7±;(3)271的立方根为31;(4)41是161的平方根。
A 、1B 、2C 、3D 、47、一个数的平方根与立方根相等,则这个数是( ) A. 1 B. ±1 C. 0 D.—18、如果333.137.23≈,872.27.233≈ ,那么30237.0约等于( ).A. 13.33B. 28.72C. 0.1333D. 0.28729、若1-x +(y+2)2=0,则(x+y )2017=( )A .﹣1B .1C .32017D .﹣3201710、若aa a a 1,,,102则<<的大小关系是( )二、填空题11、0.0036的平方根是 ,81的算术平方根是 .12、若a 的平方根为3±,则a= .13、如果一个数的平方根是a+6和2a-15,则这个数为 。
14、比较大小:15- 1(填“>”、“<”或“=”).15、比较大小:310 ________5 (填“>”或“<”).16、立方等于它本身的数是 。
人教版七年级下册第六章实数尖子生培优测试一试卷一、单项选择题(共 10 题;共 30 分)1.如图,在数轴上表示无理数的点落在()A. 线段 AB上B线.段 BC上C线.段 CD上D线.段 DE上2.在-,,,了 11,2.101101110 ...(每个 0之间多 1 个 1)中,无理数的个数是 ( )A.2个B. 个3C. 个4 D 5 个3.一个自然数的算术平方根是x,则它后边一个数的算术平方根是()A. x+1B.2 x+1C.+1D.4.以下命题:① 负数没有立方根;② 一个实数的立方根不是正数就是负数;③ 一个正数或负数的立方根与这个数的符号一致;④ 假如一个数的立方根等于它自己,那么它必定是1或0.此中正确有()个.A. 1B. 2C. 3D. 45.以下说法中,不正确的选项是 ( ).A. 3 是(﹣ 3)2的算术平方根B.是(﹣ 3)2的平方±3根C. ﹣ 3 是(﹣ 3)2的算术平方根D﹣. 3 是(﹣ 3)3的立方根6.的算术平方根是()A.4B.C.2D.7.如图,数轴上A, B 两点分别对应实数a、 b,则以下结论中正确的选项是()A. a+b> 0B. ab> 0C.D. a+ab-<b 08.已知一个正数的两个平方根分别是a+3 和 2a-15,则这个正数为()A. 4B.C. -7D. 499.晓影设计了一个对于实数运算的程序:输入一个数后,输出的数老是比该数的平方小1,晓影依据此程序输入后,输出的结果应为()A. 2016B. 2017C. 2019D. 202010.,则 a 与 b 的关系是()A. B. a与 b 相等 C. a与 b 互为相反数D无.法判定二、填空题(共 6 题;共 24 分)11.的平方根是 ________,的算术平方根是________,-216的立方根是________.12.是 9 的算术平方根,而的算术平方根是 4,则= ________.13.已知:( x2+y2+1)2﹣ 4=0,则 x2+y2 =________.14.实数 a 在数轴上的地点如图,则 |a ﹣3|=________ .15.若四个有理数同时知足:,,,则这四个数从小到大的次序是________.16.若用初中数学课本上使用的科学计算器进行计算,则以下按键的结果为________.三、计算题(共 1 题;共 6 分)17.计算:四、解答题(共 6 题;共 40 分)18.一个数的算术平方根为2M -6,平方根为± (M- 2),求这个数.19. 某公路规定行驶汽车速度不得超出80 千米 / 时,当发生交通事故时,交通警察往常依据刹车后车轮滑过的距离预计车辆的行驶速度,所用的经验公式是,此中v 表示车速(单位:千米/ 时),d 表示刹车后车轮滑过的距离(单位:米), f 表示摩擦系数.在一次交通事故中,经丈量 d=32 米,f=2.请你判断一下,闯事汽车当时能否高出了规定的速度?20. a, b,c 在数轴上的对应点如下图,化简+|c ﹣b| ﹣()3.21.阅读以下资料:∵,即,.∴的整数部分为 2,小数部分为请你察看上述的规律后试解下边的问题:假如的小数部分为a,的小数部分为b,求的值.22.规定一种新的运算a△b=ab﹣ a+1,如 3△4=3 ×4﹣ 3+1,请比较与的大小.23.求以下 x 的值.(1) 2x3=﹣ 16(2)(x﹣1)2=4.答案一、单项选择题1.C2.B3.D4.A5.C6.C7.C8.D9.B 10.C 二、填空题11. ±;;-612.19 13.1 14.3﹣ a 15.16.﹣5三、计算题17. 解:原式 =5+3-6=2四、解答题18.解:应分两种状况: ① 2M -6= M -2,解得 M= 4,2∴2M - 6=8- 6= 2,2 = 4,② 2M -6=- (M- 2),解得 M=,∴ 2M -6=-6=(不合题意 ,舍去 ),故这个数是 4.19.解:把 d=32, f=2 代入 v=16,v=16=128(km/h )∵128> 80,∴闯事汽车当时的速度高出了规定的速度20.解:依据数轴上点的地点得:a< b< 0<c,且|a|>|b|>|c|,∴a﹣ b< 0, c﹣ b> 0, a+c< 0,则原式 =|a ﹣ b|+|c ﹣ b| ﹣( a+c) =b﹣ a+c﹣ b﹣ a﹣ c=﹣2a21.解:∵<,<,∴ a=﹣2,b=﹣3,∴=﹣2+﹣ 3﹣=﹣ 522.解:∵ a△b=a ×b﹣a+b+1,∴(﹣ 3)△=(﹣ 3)×﹣(﹣ 3) ++1=4﹣ 2,△(﹣ 3) =×(﹣ 3)﹣+(﹣ 3) +1=﹣ 4﹣ 2,∵4﹣ 2>﹣ 4﹣ 2,∴﹣ 3△>△(﹣ 3).23.解:( 1)∵ 2x3=﹣ 16,2∴x =﹣ 8,∴x=﹣ 2.(2)∵(x﹣1)2=4,∴x﹣ 1=±2,∴x=﹣ 1 或 3.人教版七年级数学下册第六章实数单元检测题一、选择题。
福建省福州文博中学七年级数学下学期复习专题-复习总资料人教新课标版第5章相交线与平行线一、相交线1、邻补角:如图,错误!未找到引用源。
和错误!未找到引用源。
有一条公共边OA,它们的一边互为反向延长线,显然它们互补,具有这种关系的两个角,叫做邻补角。
2、对顶角:如图,错误!未找到引用源。
和错误!未找到引用源。
有一个公共顶点O,并且错误!未找到引用源。
的两边分别是错误!未找到引用源。
的两边的反向延长线,具有这种位置关系的两个角,叫做对顶角。
对顶角的性质:对顶角相等。
例1、已知直线AB、CD相交于点O,若错误!未找到引用源。
,求错误!未找到引用源。
和错误!未找到引用源。
的度数。
例2、如图所示,错误!未找到引用源。
和错误!未找到引用源。
是对顶角的是( )3、垂直(1)垂线的概念:两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
如图3,错误!未找到引用源。
,垂足为O 。
(2)垂线的性质:过一点有且只有一条直线与已知直线垂直。
例3、如图,∠1=150 , ∠AOC=900,点B 、O 、D 在同一直线上,则∠2的度数为( )A 、750 B 、150 C 、1180 D 、 1650(3)垂线的画法:例4、如图,直线CD 与直线AB 相交于C ,根据下列语句画图 (1)过点P 作PQ ∥CD ,交AB 于点Q (2)过点P 作PR ⊥CD ,垂足为R(3)若∠DCB=1200,猜想∠PQC 是多少度?并说明理由(4)垂线段:连接直线外一点与直线上各点的所有线段中,垂线段最短。
(垂线段最短) (5)点到直线的距离:直线外一点到这条直线的垂线段的长度。
例5、如图,能表示点到直线(或线段)距离的线段有( )A 、 2条B 、3条C 、4条D 、5条 4例6、如图,∠ADE 和∠CED 是( )A 、 同位角 B 、内错角 C 、同旁内角 D 、互为补角二、平行线5、平行线的定义:在同一平面内,不相交的两条直线叫做平行线。