抽屉原理 (3)

抽屉原理的活动设计理念：活动通过直观和实际操作，使学生进一步经历“抽屉原理”的探究过程，并对一些简单的实际问题“模型化”，从而在用“抽屉原理”加以解决的过程中，促进逻辑推理能力的发展，培养分析、推理、解决问题的能力以及探索数学问题的兴趣，同时也使学生感受到数学思想方法的奇妙与作用，在数学思维的训练中，逐步形成有序地、严密地思考问题的意识。

活动目的：1. 通过操作、观察、比较、推理等活动，让学生进一步经历“抽屉原理”的探究过程，并逐步理解和掌握“抽屉原理”。

2、会用“抽屉原理”解决生活中简单的实际问题，培养学生有根据、有条理地进行思考和推理的能力。

3.使学生经历将具体问题“数学化”的过程，培养学生的“模型”思想。

4、通过“抽屉原理”的灵活应用让学生感受到数学的魅力，并培养学生对数学的学习兴趣。

活动具体过程一、创设情境上一节课我们初步探究了抽屉原理，谁能来举一个例子，激活同学的思维？让我们在一起回顾上一节课的探究结果？学生举例后，让学生自由回答师：这节课我们继续学习这类问题。

二、提供平台，开放探究1.出示课件：把5本书放进2个抽屉里，不管怎么放，总有一个抽屉里至少有几本书？学生先独立思考，然后再小组探究，师巡视了解各种情况。

(有上一节课的探究方法做基础，这里应该学生自己能够得出结理论）2、学生汇报。

学生小组交流，让学生提出不同意见！学生汇报后，教师再和学生交流和梳理思路，引导学生把书尽量多地“平均分”给各个抽屉，看每个抽屉能分到多少本书，剩下的书不管放到哪个抽屉，总有一个抽屉比平均分得的本数多1本，并在黑板上板书：5本 2个 2本……余1本（总有一个抽屉里至少有3本书）。

3、变式思考。

出示变式题：把7本书放进2个抽屉里，不管怎么放，总有一个抽屉里至少有几本书？把9本书放进2个抽屉里，不管怎么放，总有一个抽屉里至少有几本书？学生分小组自由探究，师巡视了解情况。

4、再次汇报。

教师在学生汇报后，相应的进行板书：7本 2个 3本……余1本（总有一个抽屉里至少有4本书）；9本 2个 4本……余1本（总有一个抽屉里至少有5本书）。

4分割图形构造“抽屉”与“苹果”在一个几何图形内, 有一些已知点, 可以根据问题的要求, 将几何图形进行分割, 用这些分割成的图形作抽屉, 从而对已知点进行分类, 再集中对某个抽屉或某几个抽屉进行讨论, 使问题得到解决.命题4在正方体的8个顶点处分别放上8个不同的正整数, 如果它们的和等于55, 那么, 一定能找到某个侧面正方形, 其相对顶点所放的数都是奇数.证明 首先, 由8个正整数的和为奇数知, 当中必有奇数个奇数；其次,为奇数的至少有3个, 否则, 假设最多有一个奇数, 便有571412108642155=+++++++≥，矛盾! 现以正方体的侧面对角线为棱组成两个三棱锥, D – A 1 BC , B 1 – ACD 1如图1, 3个奇数归入2个三棱锥, 必有2 个奇数属于同一个三棱锥。

这两个归入奇数的顶点必是某一侧面正方形的相对顶点。

此命题中的抽屉原理的应用属于“苹果”(元素) 、“抽屉”都未直接给出的类型, 需要从几何上去构造两个“抽屉”。

并运用奇偶分析法找出3 个“苹果”。

在不超过60的正整数中任取9个数，证明：这9个数中一定有两个数（a 和b ）的比值满足23b a 32≤≤例3 任意给定12 个不同的自然数,证明其中必有两个数的和或差是20 的倍数.证明 将自然数按照除以20 所得的余数分类,得0、l 、2、……、19,共20 类.任意给定的12 个不同的自然数,若有两个数在同一类(即两个数除以20的余数相同),那么它们的差是20 的倍数,结论成立。

任意给定的12 个不同的自然数中,每两个数都不在同一类,也就是按上面分的20 类中每一类只多有一个已知数(也可以没有).此时,我们把自然数按被20 除的余数。

0、l 、2、3、……、19 分成11类:{I,19},{2,18},{3,17},…,{9,11},{10},{0}每一类当做1 个抽屉,己知的12 个自然数必有两个在同一个抽屉中,它们的和是20 的倍数 一般地任取22n +⎥⎦⎤⎢⎣⎡个不同的自然数，必有两个数的和或差是n 的倍数. 证明 设所给的自然数为a m （m=1、2、……、22n +⎥⎦⎤⎢⎣⎡），有a m =ng m +r m ，⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∈2n ......210r m 、、、、 则22n +⎥⎦⎤⎢⎣⎡个自然数的余数，分属12n +⎥⎦⎤⎢⎣⎡种情况，看做12n +⎥⎦⎤⎢⎣⎡个抽屉，必有两个数ai ，aj 属于同一个抽屉，即j i r r =。

抽屉原理的三个公式抽屉原理的一种更一般的表述为：“把多于kn+1个东西任意分放进n个空抽屉（k是正整数），那么一定有一个抽屉中放进了至少k+1个东西。

”知道抽屉数和至少数（同类），求物体时：物体数=（至少数-1）×抽屉数+1。

当至少数为2时，物体数=抽屉数+1。

抽屉原理，主要由以下三条所组成：原理1：把多于n+1个的物体放在n个抽屉里，则至少存有一个抽屉里的东西不少于两件。

原理2 ：把多于mn(m乘n)+1（n不为0）个的物体放到n个抽屉里，则至少有一个抽屉里有不少于（m+1）的物体。

原理3 ：把无穷多件物体放进n个抽屉，则至少存有一个抽屉里存有无穷个物体。

把它推广到一般情形有以下几种表现形式。

形式一：设立把n+1个元素分割至n个子集中(a1，a2，…，an)，用a1，a2，…，an 分别则表示这n个子集对应涵盖的元素个数，则：至少存有某个子集ai，其涵盖元素个数值ai大于或等于2。

证明：（反证法）假设结论不成立，即对每一个ai都有ai\uc2，则因为ai是整数，应有ai≤1，于是有：a1+a2+…+an≤1+1+…+1=n\ucn+1，这与题设矛盾。

所以，至少有一个ai≥2，即必有一个集合中含有两个或两个以上的元素。

形式二：设立把nm+1个元素分割至n个子集中(a1，a2，…，an)，用a1，a2，…，an则表示这n个子集对应涵盖的元素个数，则：至少存有某个子集ai，其涵盖元素个数值ai大于或等于m+1。

证明：（反证法）假设结论不成立，即对每一个ai都有ai\ucm+1，则因为ai是整数，应有ai≤m，于是有：a1+a2+…+an≤m+m+…+m=nm\ucnm+1，这与题设二者矛盾。

所以，至少有存在一个ai≥m+1。

“抽屉原理例3”教学设计设计理念本课着眼于学生数学思维的发展，注重让学生充分体验猜测验证的推理过程，努力提高他们分析和解决问题的能力。

通过实验操作、假设推理等活动，调动学生已有的生活经验，引导他们体验运用“抽屉原理”进行逆向思维的探究过程，培养学生观察比较、动手操作、逻辑推理以及语言表达等能力。

让学生在应用“抽屉原理”的过程中，感受数学的魅力，激发他们学习数学的兴趣和探求数学知识的欲望。

教学内容《义务教育课程标准实验教科书数学》（人教版）六年级下册第70、72页。

学情与教材分析例题3是“抽屉原理”的具体应用，也是运用“抽屉原理”进行逆向思维的一个典型例子。

应该把什么看成抽屉，要分放的东西是什么。

学生在思考这些问题的时候，一开始可能会缺乏思考的方向，很难找到切入点。

而且，题中不同颜色球的个数，很容易给学生造成干扰。

因此教学时，教师要允许学生借助实物操作等直观方式进行猜测、验证。

并在此基础上，逐步引导学生把具体问题转化为“抽屉问题”，找出这里的“抽屉”是什么，“抽屉”有几个，再应用前面所学的“抽屉原理”进行反向推理。

教学目标1. 通过观察、猜测、实验、推理等活动，寻找隐藏在实际问题背后的“抽屉问题”的一般模型。

体会如何对一些简单的实际问题“模型化”，用“抽屉原理”加以解决。

2.在经历将具体问题“数学化”的过程中，发展数学思维能力和解决问题的能力，感受数学的魅力。

同时积累数学活动的经验与方法，在灵活应用中，进一步理解“抽屉原理”。

教学准备一个盒子、4个红球和4个蓝球为一份，准备这样的教、学具若干份。

教学过程一、创设情境，猜想验证1.猜一猜，摸一摸。

（出示一个装了4个红球和4个蓝球的不透明盒子，晃动几下）师：同学们,猜一猜老师在盒子里放了什么?（请一个同学到盒子里摸一摸，并摸出一个给大家看）师：老师的盒子里有同样大小的红球和蓝球各4个，如果这位同学再摸一个，可能是什么颜色的？师：如果老师想这位同学摸出的球，一定有2个同色的，最少要摸出几个球？【设计意图：利用学生的好奇心理，创设摸物体的活动，激发学生的学习兴趣，为他们投入探究学习的活动做好情感铺垫。

抽屉原理(三)我们在四年级已经学过抽屉原理，并能够解答一些简单的抽屉原理问题。

这两讲先复习一下抽屉原理的概念，然后结合一些较复杂的抽屉原理问题，讨论如何构造抽屉。

抽屉原理1将多于n件物品任意放到n个抽屉中，那么至少有一个抽屉中的物品不少于2件。

抽屉原理2将多于m×n件物品任意放到到n个抽屉中，那么至少有一个抽屉中的物品不少于（m+1）件。

理解抽屉原理要注意几点：(1)抽屉原理是讨论物品与抽屉的关系，要求物品数比抽屉数或抽屉数的倍数多，至于多多少，这倒无妨。

（2）“任意放”的意思是不限制把物品放进抽屉里的方法，不规定每个抽屉中都要放物品，即有些抽屉可以是空的，也不限制每个抽屉放物品的个数。

（3）抽屉原理只能用来解决存在性问题，“至少有一个”的意思就是存在，满足要求的抽屉可能有多个，但这里只需保证存在一个达到要求的抽屉就够了。

（4）将a件物品放入n个抽屉中，如果a÷n= m……b，其中b是自然数，那么由抽屉原理2就可得到，至少有一个抽屉中的物品数不少于（m+1）件。

例1 五年级有47名学生参加一次数学竞赛，成绩都是整数，满分是100分。

已知3名学生的成绩在60分以下，其余学生的成绩均在75～95分之间。

问：至少有几名学生的成绩相同？分析与解：关键是构造合适的抽屉。

既然是问“至少有几名学生的成绩相同”，说明应以成绩为抽屉，学生为物品。

除3名成绩在60分以下的学生外，其余成绩均在75～95分之间，75～95共有21个不同分数，将这21个分数作为21个抽屉，把47-3=44（个）学生作为物品。

44÷21= 2……2，根据抽屉原理2，至少有1个抽屉至少有3件物品，即这47名学生中至少有3名学生的成绩是相同的。

例2 夏令营组织2000名营员活动，其中有爬山、参观博物馆和到海滩游玩三个项目。

规定每人必须参加一项或两项活动。

那么至少有几名营员参加的活动项目完全相同？分析与解：本题的抽屉不是那么明显，因为问的是“至少有几名营员参加的活动项目完全相同”，所以应该把活动项目当成抽屉，营员当成物品。

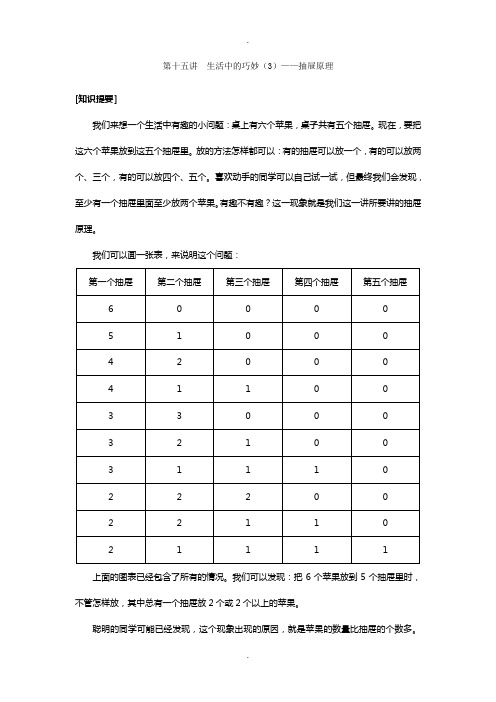
第十五讲生活中的巧妙（3）——抽屉原理[知识提要]我们来想一个生活中有趣的小问题：桌上有六个苹果，桌子共有五个抽屉。

现在，要把这六个苹果放到这五个抽屉里。

放的方法怎样都可以：有的抽屉可以放一个，有的可以放两个、三个，有的可以放四个、五个。

喜欢动手的同学可以自己试一试，但最终我们会发现，至少有一个抽屉里面至少放两个苹果。

有趣不有趣？这一现象就是我们这一讲所要讲的抽屉原理。

我们可以画一张表，来说明这个问题：上面的图表已经包含了所有的情况。

我们可以发现：把6个苹果放到5个抽屉里时，不管怎样放，其中总有一个抽屉放2个或2个以上的苹果。

聪明的同学可能已经发现，这个现象出现的原因，就是苹果的数量比抽屉的个数多。

6>5，那么一个抽屉，一个抽屉放下来，等到五个抽屉都各放了一个后，还是会有一个苹果剩下。

那么不管把它放在那个抽屉里，都会有一个抽屉里有两个。

所以，没有一个抽屉里是只有一个苹果的。

这个原理，具体写出来就是：只要苹果数>抽屉数，就会至少有一个抽屉里面至少放两个苹果。

这个原理虽然简单，但它却是组合数学中最重要的一个原理，很多大数学家也要靠它来解决问题呢！所以，掌握了它，就相当于掌握了进入数学大厦的一把金钥匙。

下面，我们看一看生活中其它应用抽屉原理的问题：[经典例题][例1]沙沙说：“我不知道我的好朋友都在几月出生，但是我可以肯定，在我的好朋友中，至少有两个人出生在相同月份。

”那么，沙沙至少有几个好朋友呢？[分析]这两个问题，刚一看时，好像和“抽屉放苹果”的问题一点关系都没有。

但是，其实也是可以利用抽屉原理来解决的。

我们知道，一年有十二个月。

其实，这十二个月就可以看成是十二个“抽屉”，沙沙的那些好朋友就可以看成是若干个“苹果”。

我们还知道，13是比12的最小的整数。

因此，为了保证在沙沙的好朋友中至少有两个人出生在相同月份，沙沙至少应该有13个好朋友。

从这道题目可以看出来，应用抽屉原理解决生活中的问题，关键的地方在于准确地发现题目中的哪个量可以被看成是“抽屉”，哪个量又可以被看成是“苹果”。

抽屉原理一、抽屉原理的定义（1）举例桌上有10个苹果，要把这10个苹果放到9个抽展里，无论怎样放，有的抽屉可以放1个，有的可以放2个，有的可以放5个，但最终我们会发规至少我们可以找到一个抽屉里面至少放两个苹果。

（2）定义一般情况下，把n+1或多于n+1个苹果放到n个抽屉里，其中必定至少有一个抽屉里至少有两个苹果。

我们称这种现象为抽屉原理。

二、抽屉原理的解题方案（一）、利用公式进行解题苹果÷抽屉=商……余数余数：（1）余数=1，结论：至少有（商+1）个苹果在同一个抽屉里（2）余数=x至少有（商+1）个苹果在同一个抽屉里（3）余数=0，结论至少有“商”个苹果在同一个抽屉里（ニ）、利用最值原理解题（最不利原则：一切最不利情况+1=成功）将题目中没有阐明的量进行极限讨论，将复杂的题目变得非常简单，也就是常说的极限思想“任我意”方法、特殊值方法。

类型：“必有2个”原理；必有m+1个”原理要点：最不利原则；保证与至少精讲例题一：某校六年级有367名学生，请问有没有2名学生的生日是在同一天?为什么?【思路导航】把一年的天数看成是抽屉，把学生数看成是元素即至少有2名学生的生日是在同一天。

把367个元素放到366个抽屉中，至少有一个抽屉中有2个元素，至少在一个抽屉里有2名学生，因此肯定有2名学生的生日是在同一天。

试一试：1.某校有370名1992年出生的学生，其中至少有2名学生的生日是在同一天，为什么?2.某校有30名学生是2月份出生的。

能否至少有2名学生的生日是在同一天?3.15个小朋友中，至少有几个小朋友在同一个月出生?精讲例题二：某班学生去买语文书、数学书、英语书。

买书的情况是:有买一本的、两本的，也有买三本的，问至少要去几名学生才能保证一定有2名学生买到相同的书?(每种书最多买一本)试一试：1.某班学生去买数学书、语文书、美术书、自然书。

买书的情况是：有买一本的，有买两本的，有买三本、四本的。

问至少去几名学生才能保证一定有2名学生买到相同的书?(每种书最多买一本)2学校图书室有历史、文艺、科普三种图书。

抽屉原理【教学内容】《义务教育课程标准实验教科书·数学》第70、71页，例1、例2.【教材分析】抽屉原理是人教版六年级下册第五单元数学广角的内容。

本单元内容通过几个直观的例子，借助实际操作，向学生介绍“抽屉原理”。

使学生在理解“抽屉原理”这个数学方法的基础上，对一些简单的实际问题加以“模型化”，会用抽屉原理加以解决。

“抽屉原理”的理论本身并不复杂，甚至能够说是显而易见的。

但“抽屉原理”的应用却是千变万化的，它能够解决很多有趣的问题，并能常常得到一些令人惊异的结果。

本单元用直观的方法，介绍了“抽屉原理”的两种形式，并安排了很多具体问题和变式，协助学生加深理解，学会利用“抽屉问题”解决简单的实际问题。

在此过程中，让学生初步经历“数学证明”的过程。

实际上，通过“说理”的方式来理解“抽屉原理”的过程就是一种数学证明的雏形，有助于提升学生的逻辑思维水平，为以后学习较严密的数学证明做准备。

还要注意培养学生的“模型”思想，这个过程是将具体问题“数学化”的过程，能从纷繁的现实素材中找出最本质的数学模型，是体现学生数学思维和水平的重要方面。

【学情分析】六年级学生既好动又内敛，教师一方面要适当引导，激发学生的学习兴趣，鼓励学生借助学具、实物操作、或画草图的的方式实行“说理”；另一方面要创造条件和机会，让学生充分发表自己的见解，发挥学生学习的主体性，重在让学生经历知识发生、发展的过程，而不是只求结论。

“抽屉原理”在生活中应用广泛，学生在生活中也常常能遇到实例，但并不能从数学的角度来理解和使用“抽屉原理”，所以教学中应有意识地让学生理解“抽屉原理”的“一般化模型”。

六年级学生的逻辑思维水平、小组合作水平和动手操作水平都有了较大的提升，加上已有的生活经验，很容易感受到用“抽屉原理”解决问题带来的乐趣。

【设计理念】本课充分利用学生的生活经验，为学生自主探索提供时间和空间，引导学生通过观察、实践、推理和交流等活动，经历探究“抽屉原理”的过程，学会用一般性的数学方法思考问题，培养学生的数学思维水平，发展学生解决问题的水平。

小学奥数系列8-2-1抽屉原理（三）一、1. 从1到20这20个数中，任取11个不同的数，必有两个数其中一个是另一个数的倍数．2. 从1，3，5，7，…，97，99中最多可以选出多少个数，使得选出的数中，每一个数都不是另一个数的倍数?3. 从整数1、2、3、…、199、200中任选101个数，求证在选出的这些自然数中至少有两个数，其中的一个是另一个的倍数.4. 从1，2，3，……49，50这50个数中取出若干个数，使其中任意两个数的和都不能被7整除，则最多能取出多少个数？5. 从1，2，3，…，99，100这100个数中任意选出51个数．证明：（1）在这51个数中，一定有两个数互质；（2）在这51个数中，一定有两个数的差等于50；（3）在这51个数中，一定存在9个数，它们的最大公约数大于1．6. 有49个小孩，每人胸前有一个号码，号码从1到49各不相同．现在请你挑选若干个小孩，排成一个圆圈，使任何相邻两个小孩的号码数的乘积小于100，那么你最多能挑选出多少个孩子?7. 要把61个乒乓球分装在若干个乒乓球盒中，每个盒子最多可以装5个乒乓球，问：至少有多少个盒子中的乒乓球数目相同？8. 将400本书随意分给若干同学，但是每个人不许超过11本，问：至少有多少个同学分到的书的本数相同？9. 有苹果和桔子若干个，任意分成堆，能否找到这样两堆，使苹果的总数与桔子的总数都是偶数？10. 在长度是厘米的线段上任意取个点，是否至少有两个点，它们之间的距离不大于厘米？11. 在米长的直尺上任意点五个点，请你说明这五个点中至少有两个点的距离不大于厘米．12. 试说明在一条长100米的小路一旁植树101棵，不管怎样种，总有两棵树的距离不超过1米．13. 在米长的水泥阳台上放盆花，随便怎样摆放，至少有几盆花之间的距离不超过米．14. 在米长的水泥阳台上放盆花，随便怎样摆放，请你说明至少有两盆花它们之间的距离小于米．15. 在边长为3的正三角形内，任意放入10个点，求证：必有两个点的距离不大于1．16. 边长为1的等边三角形内有5个点，那么这5个点中一定有距离小于0.5的两点.17. 在边长为的正方形内任意放入九个点，求证：存在三个点，以这三个点为顶点的三角形的面积不超过。