数学：苏教版八年级上：《勾股定理》课件(1)

3.1 勾股定理（1）
学习目标
1．探索勾股定理的推导过程。
2.能够将边不在格线上的图形转 化为边在格线上的图形，以便于 计算图形面积．
自学指导
认真看课本P(78-79)要求：
1．完成“操作”。
2.直角三角形的斜边、直角边有怎样 的数量关系？用字母怎么表示？
8分钟后看谁能又快又准回答上 面问题并能完成检测题。
当堂训练
完成课本P（82）习题3.1第1、2 两题。
要求：1.独立完成。 2.注意解题规范，书写工整。
归纳总结
1.直角三角形两条直角边的平方和等于 斜边的平方，即 a2 b2 c2（中未知边的长。
2.在△ABC中，∠C=90°，AB=c，BC=a，AC=b。 （1）如果a=7,b=24,求c (2)如果a=15,c=17,求b 要求：1.8分钟后独立完成。
2.注意解题规范，格式正确。
课堂小结
1.勾股定理只在直角三角形中适用。
2.勾股定理揭示的是直角三角形三边之 间的数量关系：两直角边的平方和等于 斜边的平方，不是任意两边的平方和都 等于第三边的平方。
注意：运用勾股定理时，一定要先弄清 楚哪条边是斜边，不要混淆斜边和直角 边。在分不清哪条边是斜边时，要分类 讨论，写出所有可能，避免漏解或错节。

c
b
又可以表示为：c—+—1—/—2—a—b—4
a
a
cb
c
a b
对比两种表示方法，你得到勾股定理了吗？
例1 飞机在空中水平飞行，某一时刻刚好飞到一 个男孩头顶上方4000米处，过了20秒，飞机距离 这个男孩头顶5000米。飞机每时飞行多少千米？
议一议
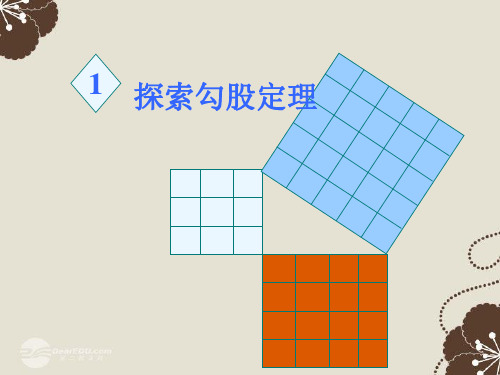
观察右图，
用数格子的方
法判断图中三 角形的三边长 是否满足
1 探索勾股定理
请同学们画四个与右图全等的
直角三角形，并把它剪下来。 a
c
b
用这四个三角形拼一拼、摆一摆，看看 是否得到一个含有以斜边c为边长的正方 形，你能利用它说明勾股定理吗？并与 同伴交流。
b 有人利用这4个直角三角
形拼出了右图，你能用两种
a
方法表示大Leabharlann 方形的面积吗？c大正方形的面积可以
表示为 ———(—a—+—b—)²———
c a
b
a²+b²=c².
(1)
a c
b
(2)
课堂练习：
一判断题. 1.ABC的两边AB=5,AC=12,则BC=13 ( ) 2. ABC的a=6,b=8,则c=10 ( ) 二填空题
1.在 ABC中,C=90°, (1)若c=10,a:b=3:4,则a=__6__,b=_8__. (2)若a=9,b=40,则c=__4_1___. 2.在 ABC中, C=90°,若AC=6,CB=8,则ABC 面积为__2_4__,斜边为上的高为__4_.8___.

谢谢观赏
You made my day!
我们，还在路上……
3.1 勾股定理
例2 [教材练习第2题变式题] 如图3－1－2，64、400分
别为所在正方形的面积，则图中字母A所代表的正方形面
积是33_6_______．
图3－1－2
3.1 勾股定理
[解析] 由图可以知道，分别以这三个正方形一边为三角形的 边，围成的三角形恰好是直角三角形，因此它们的三边满足 勾股定理，也就是说以直角边为边的两个正方形的面积和等
c2＝a2＋b2，a2＝c2－b2，b2＝c2－a2.
[注意] 只有在直角三角形中才能运用勾股定理，钝角和锐角 三角形中均不适用．
3.1 勾股定理
重难互动探究
探究问题一 利用勾股定理求单个正方形的面积或直角三 角形的边长
例1 [教材练习第1题变式题] 在Rt△ABC中，∠C＝90°， ∠A，∠B，∠C所对的边分别为a，b，c.
于以斜边为边的正方形的面积，则图中字母A所代表的正方形
面积为400－64＝336. [归纳总结] 勾股定理不仅揭示了直角三角形三边之间的数量 关系，而且揭示了以直角三角形的两直角边为边的两个正方 形的面积和与以斜边为边的正方形面积之间的关系．
3.1 勾股定理
探究问题二 综合利用勾股定理求多个直角三角形的相关边长 例3 [勾股定理运用拓展题] 一个零件的形状如图3－1－3
(1)若c＝15，b＝12，求a； (2)若a＝11，b＝60，求c； (3)若a∶b＝3∶4，c＝10，求a，b.
3.1 勾股定理
解：(1)因为 a2＋b2＝c2， 所以 a2＝c2－b2＝152－122＝81， 所以 a＝9. (2)因为 a2＋b2＝c2， 所以 c2＝112＋602＝3721， 所以 c＝61. (3)因为 a∶b＝3∶4， 所以设 a＝3x，b＝4x.

邮票的秘密 观察这枚邮票图案小方格的个数， 你有什么发现?
4
5
3
3 +4 =5
2
2
2
F
D
B
3
c 4
I
E
C H
A G
F
D
B
3
c 4
I
E
C H
A G
L
F
K I
D
B
3
c 4
E
C H
A G
J
猜想： 直角三角形中三边之间有怎样的 关系?
4 5 a c 3
3 +4 =5
2
2
2
b
2 ? a+ b= c 2 2
2 2
2
勾股史话
2 2 2 勾股定理： 勾 股 弦
勾
勾
弦 股
股
在中国古代，人们把弯曲成直角的 手臂的上半部分称为“勾”，下半部分 称为 “股”.我国古代学者把直角三角 形较短的直角边称为“勾”，较长的直 角边称为“股”，斜边称为“弦”.
商高定理 我国是最早了解勾股定理的国家之 一．早在三千多年前，周朝数学家商高就 提出，将一根直尺折成一个直角，如果勾 等于三，股等于四，那么弦就等于五，即 “勾三、股四、弦五”，它被记载于我国 古代著名的数学著作《周髀算经》中.
比一比，看看谁算得又快又准！
1.求下列直角三角形中未知边的长．
5 8 17 y
2 2 2
x
12
z 20
16
2 2 2 z + 1 6 = 2 0 1 2 =x 8 y 1 7 5+
2
2
2
y = 15
x = 13

∴ △ABC是直角三角形
b
c
(勾股定理逆定理）
C
a
B
把勾股定理送到外星
球，与外星人进行数学交流 ！ ——华罗庚
3.3 勾股定理的简单应用
交流
从远处看，斜拉桥的索塔、桥面与拉索组 成许多直角三角形．
3.3 勾股定理的简单应用
思考
A
G B CDE F
已知桥面以上索塔AB的高，怎样计算
AC、AD、AE、AF、AG的长．
3.3 勾股定理的简单应用
1、数形结合思想 2、转化思想 3、勾股定理与其逆定理在应用上的区别
•
1. 中国人只要看到土地，就会想种点 什么。 而牛叉 的是， 这花花 草草庄 稼蔬菜 还就听 中国人 的话， 怎么种 怎么活 。
•
2. 中国人对蔬菜的热爱，本质上是对土地 和家乡 的热爱 。本诗 主人公 就是这 样一位 采摘野 菜的同 时，又 保卫祖 国、眷 恋家乡 的士兵 。
竹子折断部分，用线段OB来表示 X 竹梢触地处离竹根的距离．设OA
＝x，则AB＝10－x．
O
∵∠AOB＝90°，
∴OA2＋OB2＝AB2，
∴x2＋32＝（10－x）2．
．
(10－X) B
3
3.3 勾股定理的简单应用
练习
“引葭赴岸”是《九章算术》中 另一道题“今有池方一丈，葭生其中央，出 水一尺,引葭赴岸，适与岸齐．问水深、 葭长各几何？”
•
Байду номын сангаас
7.文学本身就是将自己生命的感动凝 固成文 字，去 唤醒那 沉睡的 情感， 饥渴的 灵魂， 也许已 是跨越 千年， 但那人 间的真 情却亘 古不变 ，故事 仿佛就 在昨日 一般亲 切，光 芒没有 丝毫的 暗淡减 损。

C A
S正方形c
B C
图2-1
A
B 图2-2
（图中每个小方格代表一个单位面积）
把C“补” 成边长为6的 正方形面积的一半
1 62 2
18（单位面积）
C A
（2）在图2-2中，正 方形A，B，C中各含 有多少个小方格？它 们的面积各是多少？
B C
图2-1
A
（3）你能发现图2-1 中三个正方形A，B， C的面积之间有什么
B B′
C
D
A
E
练习1
36
如图，正方形 ABCD 的边长为 6，则图中两个
阴影部分的正方形面积之和为__________．
图放大
第4题
练习2
在△ABC 中，∠B＝90°，AB＝c, BC＝a，AC ＝b.
(1)已知 a＝6，b＝10，求 c 的长； 解：∵∠B＝90°，a＝6，b＝10， ∴c2＝b2－a2＝102－62＝64，∴c＝8.
接 CE，若 AE＝3，BE＝5，则边 AC 的长为( )
A．3
B．4
C．6
D．8
图放大
第6题
3或5
练习4
在 Rt△ABC 中，两条边的长分别为 a＝1，b＝2， 则 c2＝________．
第8题
练习5
12
如图，在等腰三角形 ABC 中，AB＝AC＝10，D 为 BC 中点，AD＝8，则 BC＝________．
3.1 勾股定理（1）
3.1 勾股定理（1）
想一想
如图，一块长约 60m、宽 约 80m 的长方形草坪，被一 些人沿对角线踏出了一条 “捷径”,请问同学们：
1．走“捷径”的客观原因 是什么？为什么？

D
B
E
A
自主拓展 4.如图：折叠直角三角形纸片ABC,使点C落在AB 上的点E处.已知BC=12 ，∠B=30°， 求DE的长.
A
E
B
DC
1B
5.假期中，小明和同学们到某海岛
上去探宝旅游，按照探宝图，
6ห้องสมุดไป่ตู้
他们登陆后先往东走8千米，
又往北走2千米，遇到障碍后 又往西走了3千米，再折向北 A
3
8
2
走了6千米处往东一拐，仅走了1千米就找到宝藏，
a bc
1 a bb a = 1 c2 2 ab
2
2
2
即 a2+2ab+b2 = c2+2ab
c a
a2+b2 = c2
b
自主合作
2.如图，把火柴盒放倒，在这个过程中，也能验证 勾股定理，你能利用这个图验证勾股定理吗？
A
bc c
D
a
C aB b E
自主合作
3.图中涂色部分是直角 边长为a、b，斜边长为c的 4个直角三角形.试利用这 个图形验证勾股定理.
可得: a2 + b2=c2 由此可以验证勾股定理.
自主探究
3.小明用这4张纸片拼成下面这个图形，你能仿照
上面的方法，利用该图验证勾股定理吗？
(a+b)2 = 4×12 ab + c2
b
a
c
即：a2 + b2 + 2ab = 2ab+c2
∴ a2 + b2 = c2
自主合作
1.你能根据下面的图形验证勾股定理吗？
初中数学 八年级(上册)
3.1 勾股定理（2）

光辉发现
我国早在三千多年前就知道了这个定理,人们把曲折成直角的手臂的上半部分称为“勾”，下半部分称为“股”，我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.因此就把这一定理称为勾股定理.
辨一辨
左图是一个直角三角形,小明,小芳和小白都说自己知道怎样描述勾股定理,请你判断他们的描述是否正确,并说明理由.
C
3、隔湖有A、Ｂ两点，从与ＢA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )
A.5米 B.12米 C.10米 D.13米
A
4.受台风麦莎影响，一棵树在离地面2米 处断裂，树的顶部落在离树根底部1.5米处，这棵树折断前有多高？
想
一
想
13 米
5 米
C
如图，小方格的边长为1.
你能求出图中正方形的面积吗？
用了“补”的方法
C
用了“割”的方法
大正方形的面积可以表示为 ；也可以表示为
(a+b)2
a2+2ab+b2 = 2ab +c2
∴a2+b2=c2
证明定理：获？2.你能运用所学的知识解决一些简单的问题吗？3.你还有哪些不懂的，或是还想要继续探索的？
数学的和谐美
方法小结
书本第79—80页练习1，2
3、在 ABC中, ∠C=90°,AC=6,CB=8,则ABC面积为_____,斜边为上的高为______.
24
4.8
13 米
5 米
2.如图,一个高3米,宽4米的大门,需在相对角的 顶点间加一个加固木条,则木条的长为（ ）
A.3 米 B.4 米 C.5米 D.6米
小明说: AB + BC = AC小芳说:小白说:

AB=15，AD=12，AC=13， 求 △ ABC 的
周长和面积。
A
A
B
D
C
B
DC
图5
图6
材料1：如图7，在△ABC中，AB=25， BC=7，AC=24，问△ABC是什么三角形？
C
A
图7
B
材料2：如图8，在△ABC中，AB=26， BC=20，BC边上的中线AD=24，求AC.
解:∵AD是BC边上的中线,
图2
沿着图2继续画直角三角形,还能得到那些无理数?
2z
5 6
3y
x2 1 1
图2
利用图2你们能在数轴上画出表示 5 的 点吗?请动手试一试！
怎样在数轴上画出表示 5 的点呢?
2z
5 6
3y
x2 1 1
图2
在数轴上表示 6, 7 ， 6, 7 的点怎样画出?
图2中的图形的周长和面积分别 是多少?
AD=12，BD=9,AC=13,求△ABC的周长和
面积。
A
周长为42 面积为84
B
D
C
图9
自学检测
1.已知四边形ABCD，∠B=90°，各边尺寸
如图所示，你能求出∠BAD的度数吗？
1D
A
3 2
┓
B2
C
勾股定理与它的逆定理在应 用上有什么区分？
勾股定理主要应用于求线段的长度、 图形的周长、面积；
∴ BD 1 BC 1 6 3
2
2
在Rt△ABC中，
B
D
C
图4
AD AB2 BD2 62 32 27 5.196
∴ SC
1 BC AD 2
1 6 5.196 15.58 15.6 2

B
C
A
1、学习勾股定理的内容及勾股定理的验证 方法(“割”、“补”法）； 2、了解有关勾股定理的历史； 3、利用勾股定理进行计算要注意利用方程 的思想求直角三角形中有关线段的长； 4、勾股定理揭示了直角三角形中三边之间 的数量关系，是运用代数知识来解决几何 问题。
感谢各位领导、专家指导!
盛开的水莲
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高
出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵
齐及水面,如果知道红莲移动的水平距离为2米 ,问
这里水深多少?
A
x2+22=(x+1)2
1
C
2
H
┓
?x
B
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高
出水面1米 ,一阵大风吹过,红莲被吹至一边,花朵
齐及水面,如果知道红莲移动的水平距离为2米 ,问
a2+b2=c2
猜想:直角三角形中两直角边a、b与斜边c 之 间的关系？
观察所得到的各组数据，你有什么发现？
SP+SQ=SR
a
bc
a2+b2=c2
猜想两直角边a、b与斜边c 之间的关系？
勾股定理 (毕达哥拉斯定理)
直角三角形两直角边的平方和 等于斜边的平方.
弦c 股b
┏
勾a
a2+b2=c2
勾股世界
求下列直角三角形中未知边的长:

比
x
一5
比 看
12
看
谁
16
x
算
得 快
20
！
8
17
x
5
X+1
x
求下列直角三角形中未知边的长: